旋波近似下光场与原子电四极矩的相互作用对原子基态的修正

纪晨晨 胡 洁

(首都师范大学物理系，北京 100048)

0 引 言

由电场的多级展开理论，刚性多极子在外电场中的势能为[1]

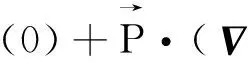
(1)

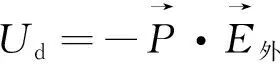
1 电偶极项对原子基态影响

1.1 光与物质耦合

由于磁场相互作用比电场相互作用弱很多，因此这里只考虑电场作用.电子处于固定轨道，只有吸收或放出光子，才会改变状态，故认为电子分布不变[2].中性原子或分子与光的相互作用常常用偶极相互作用来描述，电偶极哈密顿量为

(2)

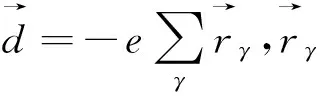
图1表示碱金属原子中的基态S电子轨道和带有激发能Ee的激发P轨道间的最低能量电偶极跃迁，即单电子激发.

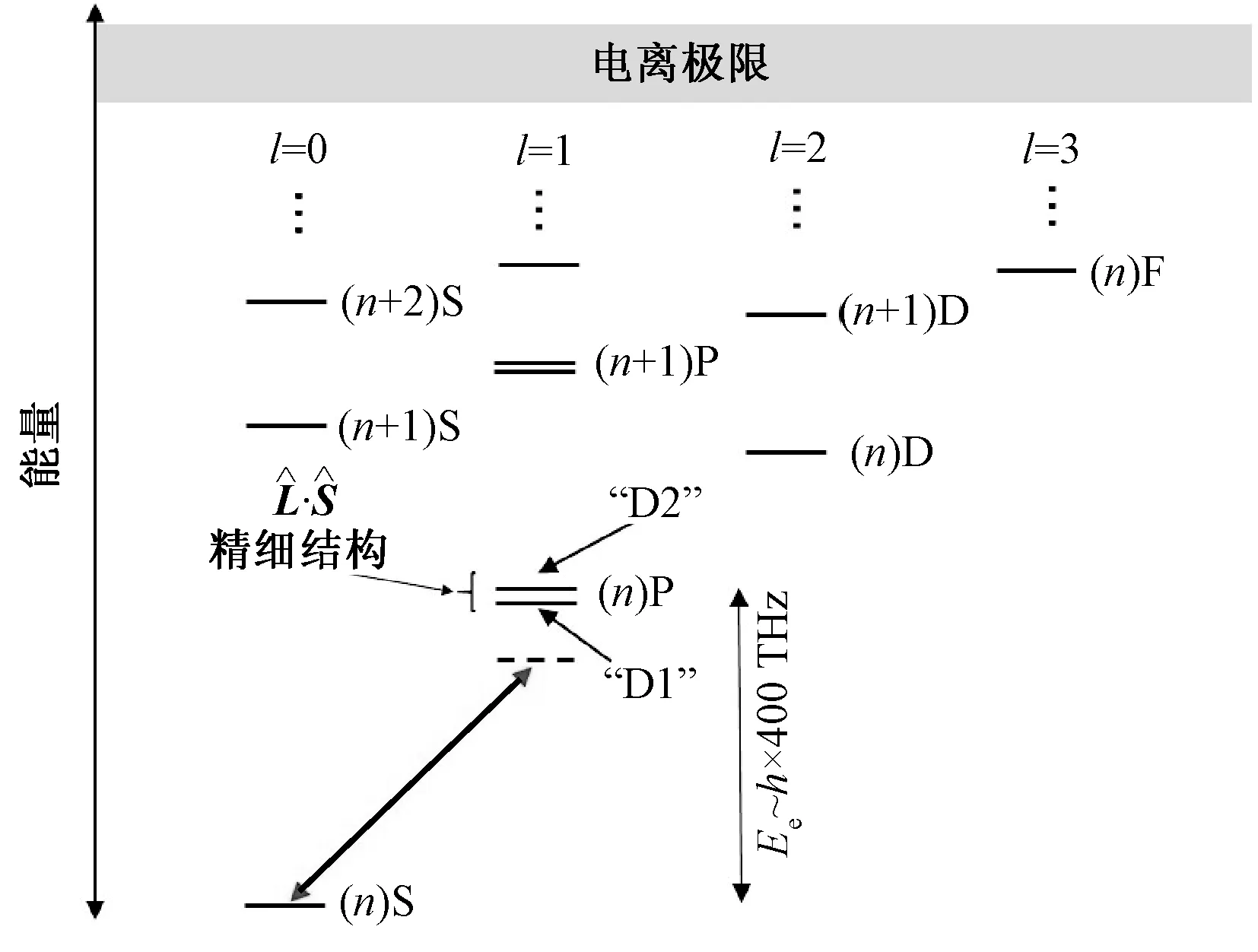
图1 典型的碱金属原子能级结构图，主要的能级跃迁在图中用粗线标注出，该跃迁是由大失谐耦合激光导致的，大小约为h×400 THz，图中也画出了远小于它的精细结构ΔFS[2]

图1中所示的(n)S态是在确定的主量子数n下的最低能级，即本文中的原子基态，考虑光与原子耦合后，该基态能级将发生变化，这个能级移动就是本文给出的光与原子耦合项引起的能量修正.

原子哈密顿量如下

(3)

故系统的总哈密顿量为

(4)

1.2 旋波近似

本文关注的失谐光场与共振区相差不远，有|Ee-ħω|≪Ee.在这个情况中，常通过如下的幺正转换形式，将原子激发态矢|e〉转换到旋转坐标系|e′〉=eiωt|e〉

(5)

(6)

旋波近似后，原子部分哈密顿量为

(7)

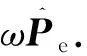
(8)

这里失谐能Δe=Ee-ħω替代了Ee.

1.3 有效原子基态哈密顿量

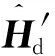
(9)

[2].

(10)

接下来讨论两种情形[2]：

1.3.1无精细结构情形

若考虑ΔFS=0，那么激发态简并，可完全忽略电子自旋和轨道的耦合作用，则有

(11)

(12)

(13)

(14)

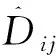
(15)

电偶极对原子基态二级修正为

(16)

运用氢原子波函数ψnlm(r,θ,φ)=Rnl(r)Ylm(θ,φ)进行计算, 将角度部分积分，得

(17)

(18)

上式称为标量光偏移[2].

这个结果只能在可妥当的忽略精细结构时才能成立，比如当Δe=Ee-ħω≫ΔFS时，这就是一个好的零级近似.该标量光移是一个与光极化无关的势，只与光振幅相关，对红失谐Δe>0的光是吸引势.这是中性原子感受到的电场造成的势场.

没有精细结构耦合的帮助，激光无法改变碱金属原子基态的自旋，这是因为激光只能改变角动量，而碱金属原子基态自旋不包含任何角动量成分.这种情形下激光造成了一个标量势，这个势只依赖于激光的总强度，而不依赖于激光的极化方向(偏振)，这就是激光俘获和光晶格的基本原理[2].Δe依赖于光频率，由于多普勒效应，它也就依赖于原子速度，这就是激光冷却的基础.

1.3.2有限精细结构情形

精细结构包括自旋轨道耦合作用以及与电子自旋无关的相对论修正部分，氢原子的相对论效应比较显著，尤其是其S能级，碱金属原子能级的精细结构没有计入这部分效应[5].

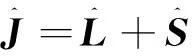
(19)

(20)

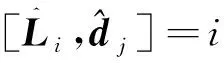
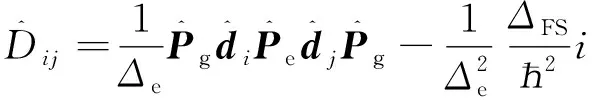
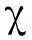
(21)

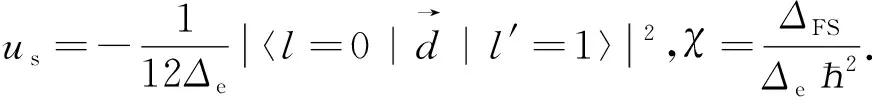
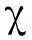
(22)

有效哈密顿量为

(23)

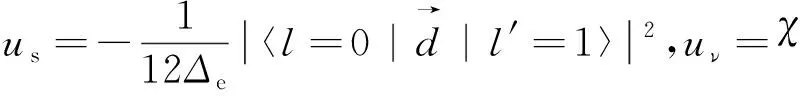
2 电四极项对原子基态影响

2.1 光与物质耦合

上一节中我们讨论了偶极项对碱金属原子基态的影响，但是忽略了电多极矩的影响，现有的涉及光与物质相互作用的研究均只考虑了电偶极项，因此我们想讨论在何情况中，电四极项作为微扰项对基态会有不可忽略的影响.

我们假设了一个处于基态的碱金属原子，原子核位于笛卡尔坐标系原点，最外层电子的位置为(d1,d2,d3).系统的电四极矩张量为

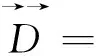
(24)

(25)

电四极子在外电场中的势能为

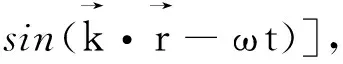
(26)

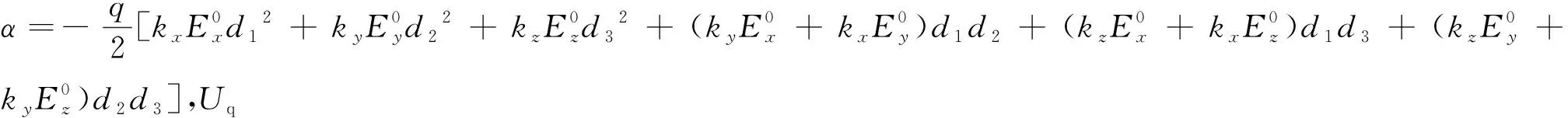
(27)

原子哈密顿量为

(28)

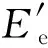
2.2 旋波近似

然后同1.2中的(6)式处理方式，对上式进行旋转波近似：

(29)

旋波近似后的原子哈密顿量同(7)式，为

(30)

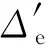
2.3 有效原子基态哈密顿量

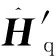
(31)

接下来讨论几种情形：

2.3.1无精细结构情形

考虑ΔFS=0，则有

(32)

(33)

电四极项对原子基态二级修正为

(34)

运用类氢原子波函数ψnlm(r,θ,φ)=Rnl(r)Ylm(θ,φ)进行计算，将角度部分积分，得

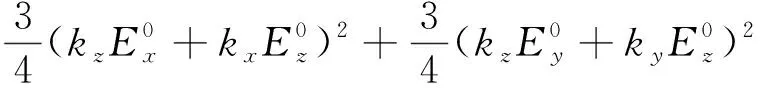
(35)

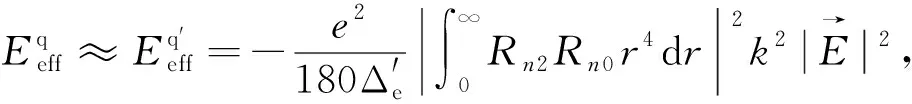
(36)

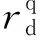
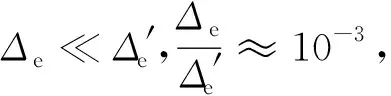
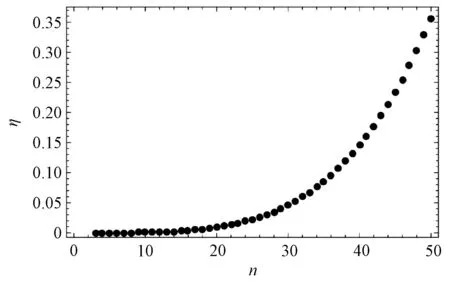
图2 η随n变化示意图

可见，在这个情况中，电偶极矩对基态的影响远大于电四极矩，因此相对于电偶极矩，电四极矩对基态的影响可忽略不计.

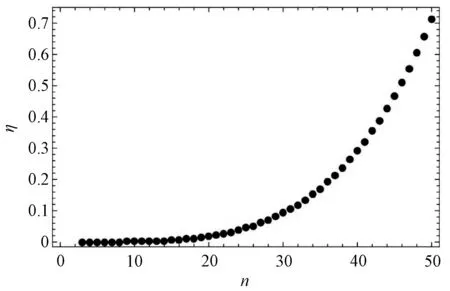
图3 η随n变化示意图

可见，随着n的增大，电四极矩对基态的影响会进一步增大.此时相对于电偶极矩，电四极矩对基态的影响达到了远大于电偶极矩的级别，电偶极矩的影响可被忽略.在上一个波长取为600 nm的情况下，电偶极矩带来的影响远远超过电四极矩，这和该情况是相反的，也就是说，这两种情况中，电偶极和电四极的影响并不会同时呈现，当一方作用明显时，另一方的效应就被压制.

η也和波矢k有关，它和波长平方成反比，也就是说，减小光场的波长也会使得电四极矩势能项增加.

根据既有的电场理论我们知道，电四极子的势能与外场的变化率有关，也就是说波长相对原子尺寸越小，电四极子势能项越大，对于尺度较小的一般微观粒子，外电场在这范围内缓变的条件常能成立，因此能用点电荷和偶极子的势能来代表整个系统的势能.当涉及到尺度较大的里德堡原子时，波长相对其原子尺度较小，因此它的电四极势较大.这一点和本文计算得到的结论是相吻合的.

2.3.2有限精细结构情形

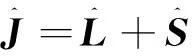
考虑Hq′对基态的二阶微扰，有

(37)

(38)

(39)

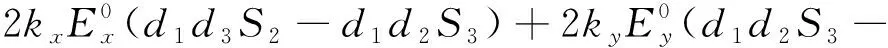
d1d3S3-d32S1)．

(40)

在加了精细结构的情况中，我们取磁场为0，但是要严格讨论这一项，还需考虑加了磁场的塞曼效应[9]，因此在本文中对加了精细结构的这一项暂不进行详细讨论.

3 结 论

在本文中，我们运用旋波近似等方法，主要研究并对比了不同原子序数的碱金属原子的电偶极项和电四极项与光场相互作用对与原子基态的影响，发现随着主量子数n的增大，电偶极矩和电四极矩对基态的影响会随之增大，在光场模长不同的情况下，电偶极和电四极的影响并不会同时呈现，当一方作用明显时，另一方的效应就被压制.此外，减小光的波长也会使得原子电四极势增大.