扣件系统频变和温变特性对钢轨振动特性的影响

李晓斌，张 勇

(1.陕西铁路工程职业技术学院，陕西渭南 714099；2.西南交通大学土木工程学院，成都 610031)

近年来，随着我国轨道交通建设的高速发展，高铁和地铁引发的环境振动和噪声问题也日益严重。在轨道的结构振动中，钢轨是主要的振动源，也是主要的噪声辐射源[1]。钢轨作为车辆系统和轨道系统的直接接触部分，其振动形态不仅影响轮轨的接触状态，而且直接关系到轮轨系统和轨道结构系统行车安全、振动控制及结构可靠性能[2]。随着高速铁路运行速度的提高，其引起的轮轨激振频率也在不断提高，由此也引发了一系列诸如钢轨波磨、多边形车轮磨耗等高频振动病害问题。为了更有效地控制高速铁路钢轨振动及其引起的辐射噪声以及与钢轨振动有关的诸多钢轨病害，必须掌握钢轨在各个频率振动的特点及传递特性。

扣件系统作为钢轨和轨枕(或其他轨下基础)的联结件，其力学性能直接影响着钢轨的振动特性。国内外许多学者从不同的角度建立了钢轨-扣件系统模型，研究扣件系统参数对钢轨振动特性的影响[3-7]。而这些研究均将扣件系统考虑为一个无质量的刚度-阻尼系统。事实上，提供扣件系统刚度和阻尼特性的是弹性垫板，一般由高分子聚合而成，其动态刚度和阻尼特性与频率和温度密切相关，而且温度和频率对其动力性能的影响在一定程度上表现出相似性[8]。上述等效刚度-阻尼系统只能在低频范围内近似描述弹性垫板力学性能，无法准确描述扣件系统动力特性的频变和温变特性，更无法揭示钢轨的高频振动特性。因此，要想精确地研究钢轨-扣件系统在宽频范围内的振动情况，必须考虑扣件系统力学性能的频变和温变特性。

本文采用分数阶KV模型表征扣件系统弹性垫板的频变动力性能，并基于分数阶KV模型建立了钢轨-扣件系统振动模型，采用格林函数法计算了不同温度下钢轨在0～3 000 Hz频率范围内的振动和传递特性，并与等效刚度-阻尼系统(普通KV模型)进行了对比。研究旨在为准确评估钢轨宽频振动特性，进一步研究高速铁路钢轨振动和噪声控制及其他振动相关问题提供理论依据。

1 扣件系统温频变力学特性及其本构模型

扣件系统主要由扣压件和弹性垫层等部件组成，扣件系统的力学性能由弹性垫层提供。弹性垫层属于高分子黏弹性材料，其动力性能具有强烈的频率和温度依赖性。为准确描述扣件弹性垫板的宽频域、宽温域动力特性，必须建立反映扣件弹性垫板黏弹性特性的数学模型。

目前，能够描述弹性垫板温频变特性的模型主要包括经验模型和本构模型。经验模型是基于实验数据的曲线拟合。首先根据实验曲线构造相应的函数式，然后求解函数参数。杨松等[9]基于黏弹性材料的力学性能，研究了ZN-17黏弹性材料动力特性随温度、频率的变化规律，并根据实验结果用指数函数拟合出了黏弹性材料动态特性的数学表达式。这种方法拟合精度高，但模型缺乏物理理论依据，参数也没有明确的物理意义[10-11]。本构模型是根据高分子材料的黏弹性本构关系推导出动力特性与温度、频率等关系的一种模型，主要是以传统机械模型或分数导数模型为基础的一系列衍化模型。Lin等[12]采用标准机械模型与橡胶的分子结构相结合建立模型，准确地描述橡胶的刚度和阻尼特性，但存在需辨识的参数多，计算量大等问题。周雄等[13]采用分数阶KV模型描述了硫化橡胶在不同温度和较宽频率范围内的动态力学行为。分数导数模型因仅用少量参数即可描述材料的黏弹性而广受学者青睐。本文将采用分数阶KV模型描述扣件系统的温频变动力特性。分数阶KV模型和普通KV模型如图1所示，时域本构方程分别见式(1)和式(2)。

(1)

F=Kαx+Cαxα

(2)

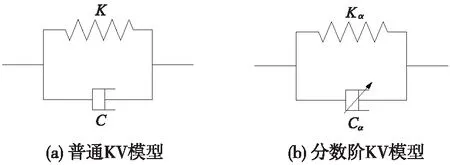
图1 扣件系统力学本构模型

2 钢轨扣件系统动力学模型

将钢轨视为弹性Euler梁，通过扣件系统直接与基础连接，如图2所示。扣件系统分别采用普通KV模型和分数阶KV模型模拟，在频域内建立钢轨扣件系统垂向动力学微分方程，然后采用格林函数法求解钢轨运动偏微分方程，可得到钢轨的点导纳和任意位移导纳。

图2 钢轨扣件系统示意图

2.1 离散弹性支承轨道模型

设钢轨为由N个扣件支撑的Euler梁，x为钢轨纵向坐标/m，zr(x，t)为t时刻时x处钢轨的垂向位移/m，则钢轨的振动微分方程可表示为

Pjeiωtδ(x-xj)

(3)

式中，mr为单位长度钢轨质量，kg；E为弹性模量，MPa；I为钢轨截面惯性矩，m4；Frsi为第i个扣件对钢轨的作用力，N；Pj为作用在钢轨xj位置的激振力幅值，N；δ(x)为Dirac函数。

扣件系统采用普通KV模型和分数阶KV模型模拟时，扣件力Frsi的表达式分别如式(4)和式(5)所示。

(4)

(5)

采用分离变量法，可将钢轨的位移响应表达为

zr(x，t)=Zr(x)eiωt

(6)

由式(3)～式(6)，可得到如下方程

(7)

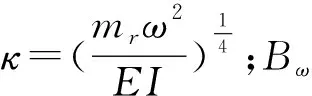
2.2 建立目标函数

采用格林函数法求解弹性钢轨Euler梁的振动。设格林函数G(x，ξ)为单位力作用点在ξ时在x处钢轨的振动响应，则由式(7)可得

(8)

由叠加原理可知，钢轨在任意x处的垂向位移响应为

(9)

式中，F(ξ)为作用在ξ处的合力。

根据式(7)和式(9)可得到

(10)

根据Dirac分布函数性质，可知在x处的钢轨垂向位移响应为

PjG(x，xj)

(11)

由式(11)可得任意一点处的钢轨垂向位移响应应为每个轨枕上方钢轨垂向位移响应的叠加，则N个轨枕上方的钢轨垂直位移响应为

PjG(xl，xj)l=1，2，…，N

(12)

设Gi，j为第j个轨枕处的单位力作用在第i个轨枕上方产生的钢轨响应，则式(12)可以用矩阵形式表示为

(INN+Gr)Zr=GjPj

(13)

式中，INN为N×N维的单位矩阵；Zr为轨枕上方钢轨垂向位移向量；Gr为轨枕处格林函数矩阵；Gj为激励作用处格林函数矩阵。

根据式(8)及Euler梁在ξ处的连续性条件得到离散支承弹性轨道模型基于格林函数法的精确解为[14]

(14)

结合式(9)和式(14)可得任意位置xi处钢轨垂向位移Zr(xi)。设激振力为单位力，可得到钢轨的位移导纳为

(15)

3 钢轨扣件系统钢轨振动特性

为分析扣件系统温频变动力特性对钢轨振动特性的影响，本文选用60 kg/m钢轨、Vossloh 300扣件系统、支承间距为0.6 m的参数，建立了钢轨扣件系统动力学模型，在相邻两扣件中部对钢轨施加单位简谐荷载，分别计算考虑扣件系统温频变特性(分数阶KV模型)和不考虑扣件系统温频变特性(普通KV模型)工况下不同频率钢轨的位移导纳，研究扣件系统的频变和温变动力特性对钢轨振动特性的影响。本文采用的钢轨模型参数和扣件模型参数如表1和表2所示。

表1 钢轨模型参数取值

表2 扣件系统模型参数

3.1 扣件频变特性的影响

计算20 ℃扣件系统分别采用普通KV模型和分数阶KV模型时钢轨振动位移导纳，可得到激励位置处钢轨位移导纳随频率变化的曲线，如图3所示。在不同频率钢轨的振动中，存在两种典型频率振动：钢轨垂向共振和钢轨pinned-pinned振动。其中，钢轨发生垂向共振时，钢轨从激励点两侧开始上翘，此时频率对应图中的第一个峰；钢轨的pinned-pinned振动指两根轨枕之间钢轨受到激励后产生机械波的节点刚好在轨枕支承处，其一阶pinned-pinned振动频率对应图中的第二个峰。

从图3可以看出，考虑扣件系统频变特征后，钢轨的共振频率由144 Hz后移到179 Hz，增大24.3%，其对应的位移导纳由1.94×10-8m/N变动为3.69×10-8m/N，增大90.2%。根据文献[7]，钢轨共振频率只与钢轨单位长度质量和单位长度轨下分布刚度有关。结合图3分析认为，扣件刚度随频率的增大而增大，导致钢轨共振频率的后移；然而，考虑扣件特性后钢轨的一阶pinned-pinned振动与不考虑扣件频变特性完全一致，频率和位移导纳均为1 443 Hz和7.67×10-9m/N，是因为钢轨梁模型垂向pinned-pinned振动频率只与钢轨自身特性有关，与轨下支承无关。同时也发现，考虑扣件频变特性后，钢轨在500 Hz的振动受频率影响较大，有较强的频率敏感性，这是因为高频时扣件系统阻尼很小，对高频能量的消耗能力减弱，钢轨振动加剧。

图3 激励处钢轨位移导纳

结合CRH380系列列车参数，根据钢轨在不同频率下振动的计算结果，提取激励点以及距激励点2.5、17.5、20 m四个不同位置截面的垂向位移导纳，分析钢轨振动在沿长度方向传递过程中的变化及其对列车其他轮对的影响。计算结果如图4所示。可以看出，不管是否考虑扣件频变特性，随着距加载点距离的增大，钢轨位移导纳减小，钢轨振动沿长度方向发生衰减。值得注意的是，当大于钢轨共振频率时，钢轨振动衰减明显减小，可见，沿长度方向，钢轨对小于钢轨共振频率的振动衰减较好，对大于共振频率振动的衰减较差，并且对钢轨pinned-pinned振动无影响。

图4 距加载点不同位置时钢轨位移导纳

3.2 扣件温变特性的影响

计算不同温度下钢轨振动沿长度方向的传递特性，可分析扣件系统温变特性对钢轨振动及其传递特性的影响。这里给出20、-10、-30 ℃下钢轨激励处和距激励点20 m处的钢轨位移导纳，如图5所示。就钢轨激励处钢轨振动情况来看，随着温度降低，钢轨位移导纳随频率变动曲线向右下方移动，其共振频率由20 ℃的179 Hz，增大到-10 ℃的224 Hz，增大到-30 ℃的294 Hz，而位移导纳由20 ℃的3.69×10-8m/N，减小到2.03×10-8m/N，减小到1.16×10-8m/N。温度降低后，扣件系统的刚度的增大引起钢轨共振频率升高，阻尼的增大提高了扣件系统的耗能性能，引起钢轨位移导纳减小。

对比钢轨激励处和距激励点20 m处的钢轨位移导纳可以发现，当激振频率小于共振频率时，温度对距加载点20 m处钢轨的位移导纳基本无影响，而当激振频率大于共振频率时，距激励点20 m位置钢轨位移导纳随温度的降低而减小。

图5 不同温度下模型激励处钢轨位移导纳

4 结论

本文考虑了扣件系统的频变和温变特性，基于钢轨扣件系统动力学模型和格林函数法推导了频域内钢轨任意位置位移导纳，分析了扣件系统频变和温变特性对钢轨振动及其沿钢轨长度方向的传递特性的影响，克服了以往钢轨振动分析不考虑扣件系统频变和温变特性的不足。所得结论和建议如下。

(1)扣件系统的刚度和阻尼具有强烈的频率和温度敏感性。在一定频率范围内，扣件刚度随频率增大而增大，阻尼随频率增大而减小。在一定温度范围内，扣件刚度和阻尼均随温度的降低而增大。

(2)扣件系统频变特性不仅会增大钢轨共振频率，而且加剧钢轨大于共振频率的高频振动响应。忽略钢轨的频变特性会严重低估钢轨的高频振动，因此，在钢轨高频振动特性研究中，扣件系统频变特性不可忽略。

(3)扣件系统温变特性会使钢轨位移导纳随频率变动曲线整体向右下方移动。低温有助于减弱钢轨小于共振频率的低频振动响应，但会增加钢轨大于共振频率的高频振动响应。就高速铁路而言，线路跨越温区大，在设计和施工时应考虑扣件弹性垫层的温变特性对钢轨振动及行车性能的影响。