基于A*优化算法的停车场动态泊车研究

，，

(浙江工业大学 信息工程学院，杭州 310023)

0 引言

随着城市发展和人民生活水平的提高，中国汽车保有量呈直线上升趋势，由此导致的城市停车难、停车效率低等一系列问题也加速了停车诱导系统的发展，其中常用的路径规划算法有Dijkstra算法、A*算法等。在动态网络路径规划算法的研究中，国外Chabini[1]等人首次引入A*算法，国内晏克非教授[2]团队结合改进的A*算法，将整个路径规划过程分成一段段按时间连续的分段，并对每个分段内的动态路网信息做静态化处理，以此解决了具有变化因素的动态路径规划问题。目前城市停车诱导系统大都应用于交通路网中车辆的路径诱导和规划，仅仅把泊车用户引导到车库的门口，针对大型停车场内部停车诱导问题的研究相对缺乏[3]。尤其是随着城市现代停车场结构的大型化和复杂化，在停车高峰期由于车位状态是实时变化的，停泊用户需要不断盲目的寻找车位，此类动态泊车问题大大增加了用户的停车时间，降低了停车效率。

针对目前停车诱导系统的不完善、车位利用率以及停车效率低[4]等问题，本文以大型停车场的内部结构模型为应用实例，把动态泊车导致的停车效率问题转化为泊车概率问题，通过对目前路径规划算法比较[5]最终选择A*算法并进行了优化，最后在VC++6.0环境下对优化后的算法做仿真和实验验证。

1 停车场结构及车位模型

1.1 停车场结构模型分析

停车用户在停车时往往遇到很多问题，其中停车效率、停车舒适性、驾驶以及行走距离等问题是影响停车用户体验的主要因素，本文结合图1地下停车场内部车位结构特点对以上问题进行了分析，从图中可以知道，地下停车场的车位分布具有以下三个主要的特点[6]。

1)停车场的车位大部分具有对称分布特性。

2)停车场内部的道路分支一般较多，一排车位的两端必定为道路的交叉口或者拐点，另外目前地下停车场的入口有很多，包括车辆驶入以及电梯等主要入口。停车位置的选择很大程度上决定了停车舒适性[8]、驾驶以及行走的距离，所以将图1中的道路交叉口、电梯、停车场车辆驶入口等标记为点，以便用户更加直观灵活的选择停车位。

3)停车场内部大部分的车位呈区域性密集分布，当泊车用户行驶到一个停车区域内时，可以明显的观察到某个车位附近的所有可用空车位从而使泊车用户车位的选择具有多样性，利用车位的这种密集分布特性我们可以大大挺高用户的动态泊车概率，进而增加停车效率。

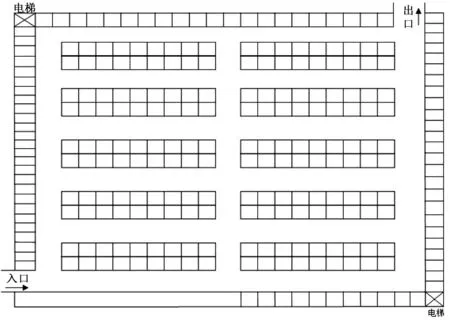
图1 地下停车场车位分布示意图

1.2 停车位模型

为了更具体化的研究A*算法在动态停车路径规划中的应用，需将道路交叉口、电梯、停车位、停车场车辆驶入口简化为节点，于是，停车场整体的网络结构就转化为有向(无向)带权图[6-7]，如图2所示。其中，阿拉伯数字(0～99)表示停车位的节点集合，Ci表示电梯、路口拐点、停车场车辆入口的节点集合，任意两个节点间的路段为边，边的权值另行存储，不在带权图中显示。结合图1停车场内部车位对称性的特点，将部分路段的上下两排车位节点合并成一排，以减少需要遍历的总节点数。

针对节点信息的存储，所有节点都按照(x,y)坐标的形式进行标记,将相邻两个节点间对应的x,y坐标差的绝对值之和作为表征两个节点间边的权值量化[9]，权值为A*算法路径规划做数据支撑，其数据准确性在一定程度上决定了算法精确度。

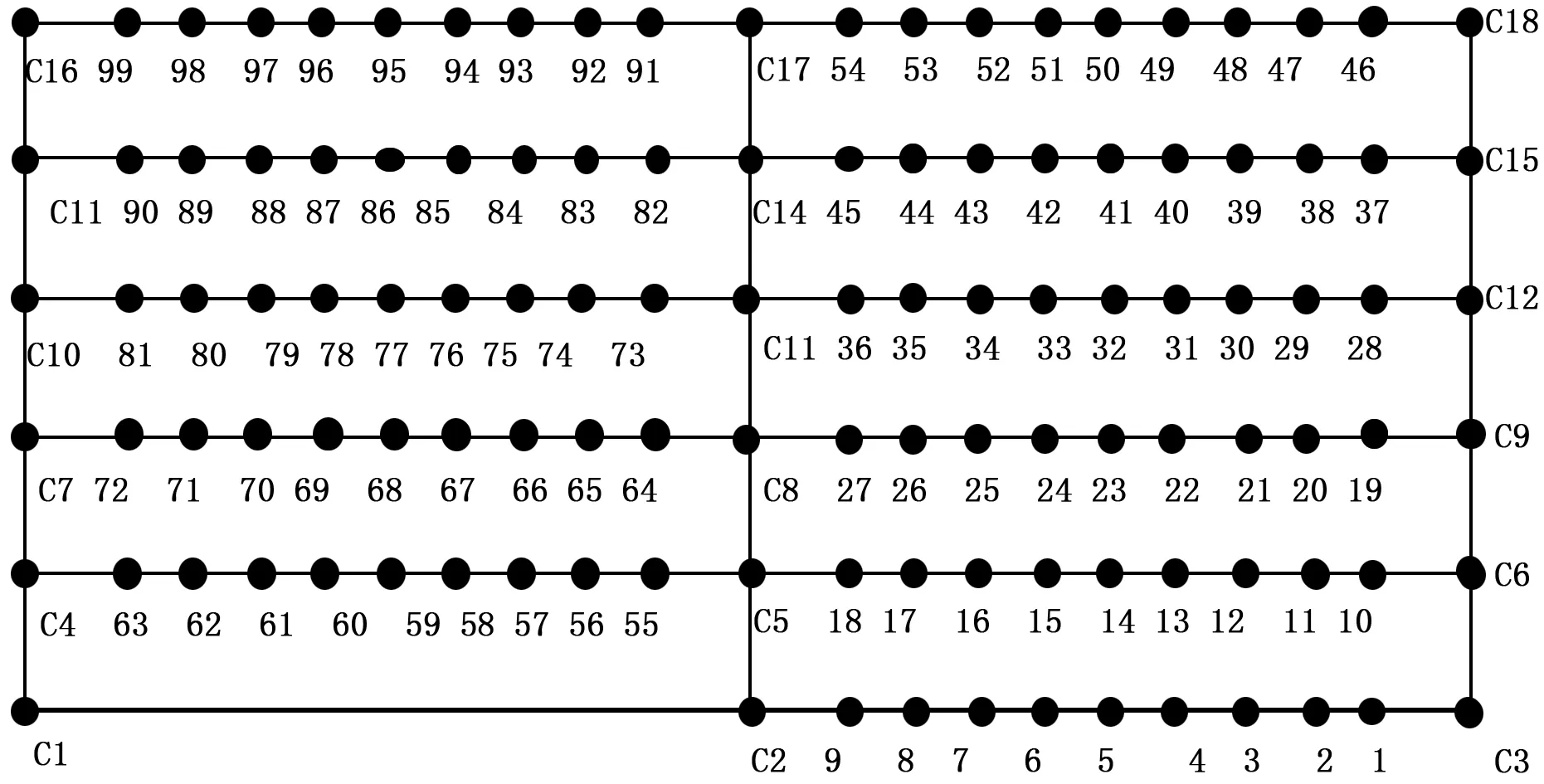
图2 停车位及路段带权图

2 路径规划算法选择

目前，地下停车场中常用的路径规划算法主要有Dijkstra算法、A*算法等。

Dijkstra[7-10]算法是经典的最短路径算法，用于求任意两个节点间的最短路径。算法的基本思想为：把带权图中所有的车位节点集合分成两个组，第一组为所有未遍历顶点集合N，第二组为已求出最短路径的顶点集合G，初始时G中只有源节点，对与G相连的节点进行扩展，选择代价最小的路径，就将它对应的顶点放入到集合G中，循环扩展直到全部顶点都放入到G中。

A*算法[13]是基于经典Dijkstra的一种启发式搜索算法，通过估价函数来约束其搜索方向，可定义A*算法的估价函数为[11]

f(n)=g(n)+h(n)

(1)

式中,f(n)为当前节点的路径代价估计；g(n)为初始节点到临时节点n的实际路径代价；h(n)为临时节点n到目标节点的路径代价估计。A*算法的基本思想为[12]：创建OPEN表、CLOSED表，OPEN表用以保存所有扩展的节点，CLOSED表用以记录已访问过的节点。初始时将源节点S放入OPEN 表中，对与S相连的节点进行扩展并放入OPEN表，取出OPEN表中具有最小估价函数值的临时节点n并放入CLOSED表中，循环扩展临时节点n直到目标节点放入CLOSED中。

综上所述，相比于经典Dijkstra算法的全节点遍历，得益于A*算法启发函数的约束，A*算法更加灵活的按照其估价函数进行启发式搜索，从而大大减少其遍历的节点数，提高了算法搜索效率。在路径最优解方面，Dijkstra算法保证找到最优路径，而启发式函数h(n)的选取决定了A*算法的精确度[11]，h(n)的选取主要有以下三种情况：

1)当h(n)小于临时节点n到目标节点的实际路径代价时，搜索的车位节点数多，算法搜索效率低，但能求得最优解。

2)当h(n)等于临时节点n到目标节点的实际路径代价时，搜索将严格按照最短路径进行，此时的算法搜索效率最高。

3)当h(n)大于临时节点n到目标节点的实际路径代价时，搜索的车位节点很少，算法搜索效率高，但是不保证求得最优解。

结合停车位及路段带权图，考虑到节点的坐标存储特性，故启发式函数h(n)采用曼哈顿(Manhattan)距离[14]，其表达式为：

h(n)=|xA-xB|+|yA-yB|

(2)

其中：(xA,yA)表示临时节点A的坐标值；(xB,yB)表示目标节点B的坐标值。

由图2的结构可知，h(n)总是小于等于临时节点n到目标节点的实际路径代价，因此保证泊车用户能按照最优路径进行泊车。综合以上分析，本文采用A*算法进行动态泊车试验的研究。

3 A*算法的优化和实现

3.1 优化A*算法

在正常泊车的过程中由于空车位的实时变动性以及随机分布性，当泊车用户随机选取单个空车位作为目标节点进行路径规划时，车位的频繁变更直接影响泊车用户的泊车成功概率以及体验。针对这一问题，本文提出了带约束条件的A*优化算法，基本思想：由获知的空停车位信息以及节点的坐标特性，对空车位比较密集的不同矩形区域分别进行限定[15-17]，并选取矩形区域中具有最小x坐标的节点作为此区域的目标节点。此最小x坐标的节点代表整个矩形区域中所有可用的空车位节点，由带权图2可知，从入口初始节点C1开始搜索时，只需要搜索到具有最小x坐标的节点即可，故在进行路径规划时选其作为目标节点很大程度上减少了遍历节点的总数，提高了算法搜索效率。同时按照停车场车位密集分布特性，矩形区域之内可用的空车位较多，在停车位具有动态变化因素的情况下，大大增加了泊车用户的泊车成功概率，保证了泊车用户车位选择的多样性和泊车体验。

由停车位的概率分布特性，泊车成功概率可定义为：

Pa=1-(m)na

(3)

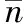
3.2 A*优化算法的实现

由仿真给定的空车位的实时信息，根据车位节点之间的坐标特性，将相邻空车位节点间坐标差值的绝对值作为矩形区域限定的度量依据，分别对空车位分布较密集的区域进行限定，最终选择目标节点并进行路径规划，通过不断扩展具有最小估价函数值f(n)=Min{f(n)}的临时节点BestNode，直至目标节点并输出目标节点的泊车概率和遍历节点总数。

算法实现的具体步骤如下。

Step 1：对空车位分布比较密集的区域分别进行矩形限定并标记，随机选取一个矩形限定区域，将此区域中具有最小x坐标的节点作为目标节点。

Step 2：创建空的OPEN、CLOSED表，并将初始节点S放入OPEN表中，设f(c1)=0。

Step 3：若OPEN表为空，初始化失败，退出程序。

Step 4：将初始节点S记为算法规划的第一个节点BestNode，并将其放入CLOSED表中。

Step 5：判断第一个节点BestNode是否为目标节点，若是则输出最短路径、停车成功概率以及遍历的节点数，否则执行下一步。

Step 6：扩展BestNode节点，选择f(n)=Min{f(n)}的节点作为下一个BestNode。

Step 7：判断当前的节点BestNode是否为目标节点，若是则输出最短路径、停车成功概率以及遍历的节点数，否则执行第6步。

Step 8：循环第6、7步直到目标节点放入到CLOSED表中，输出最短路径、泊车成功概率以及遍历的节点数。

4 仿真结果与实验分析

基于优化后的A*算法，以VC++6.0环境为实验平台，结合实际停车场中空车位的不确定性和动态性，对停车场泊车成功概率以及算法搜索效率进行了研究。通过存储的车位以及交叉路口等节点信息画出节点图，仿真给定随机空车位的信息，并由随机空车位的节点坐标信息进行矩形区域限定，随机选取其中一个区域限定的目标节点，最终进行动态泊车路径规划，同时由所选矩形区域中的可用节点数计算出泊车成功概率和算法搜索效率。其中规划的最短路径用绿色线条标出，限定区域用矩形标出，最终仿真结果如图3所示。

图3 仿真结果示意图

由上面的概率定义可知，Pr、Pa分别为优化前和优化后的泊车成功概率，其实验结果如下表所示。

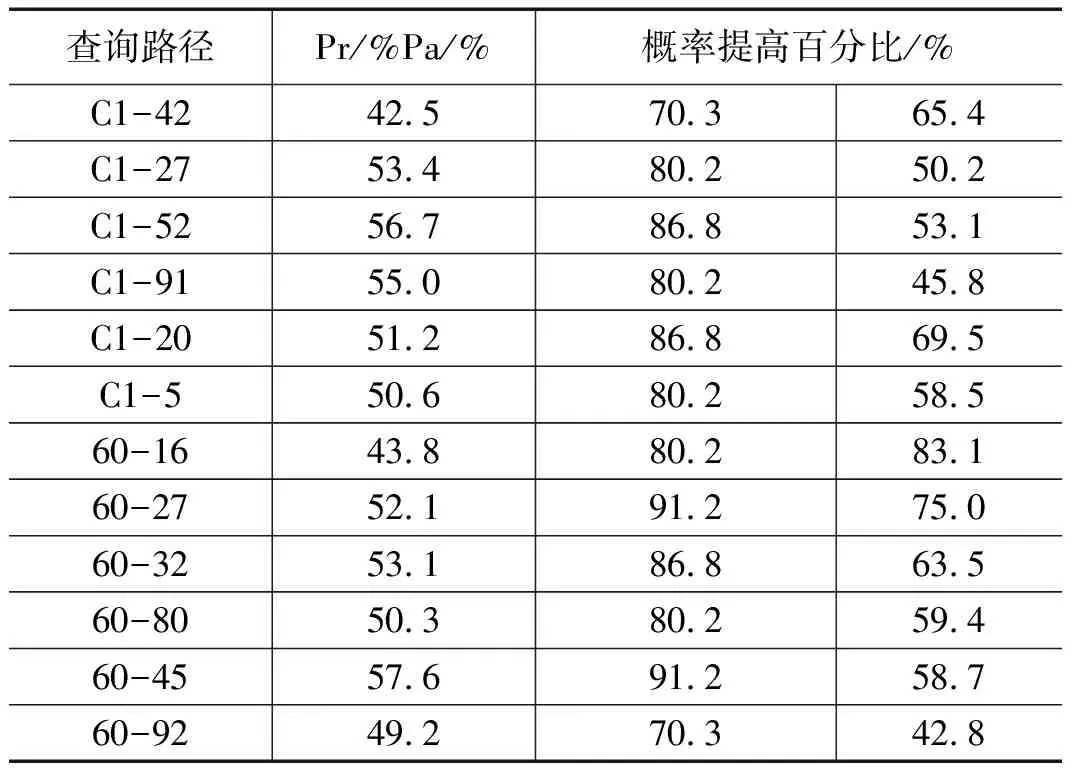
表1 A*算法优化前与优化后的泊车成功概率比较

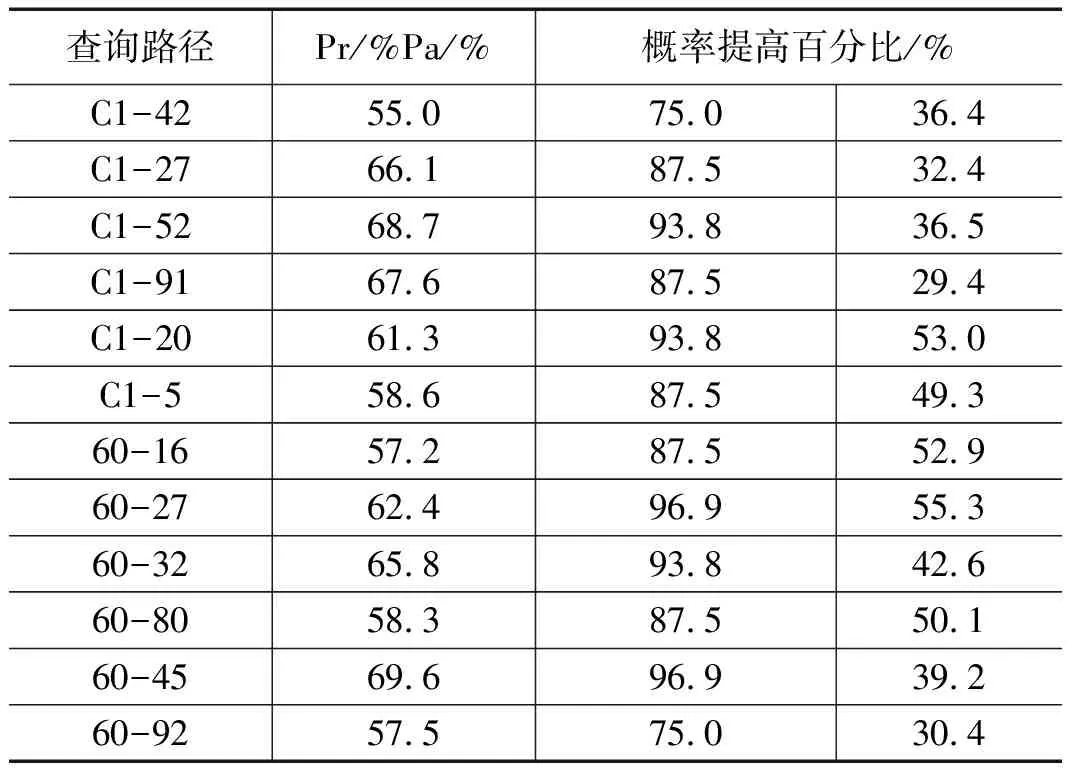
表2 A*算法优化前与优化后的泊车成功概率比较

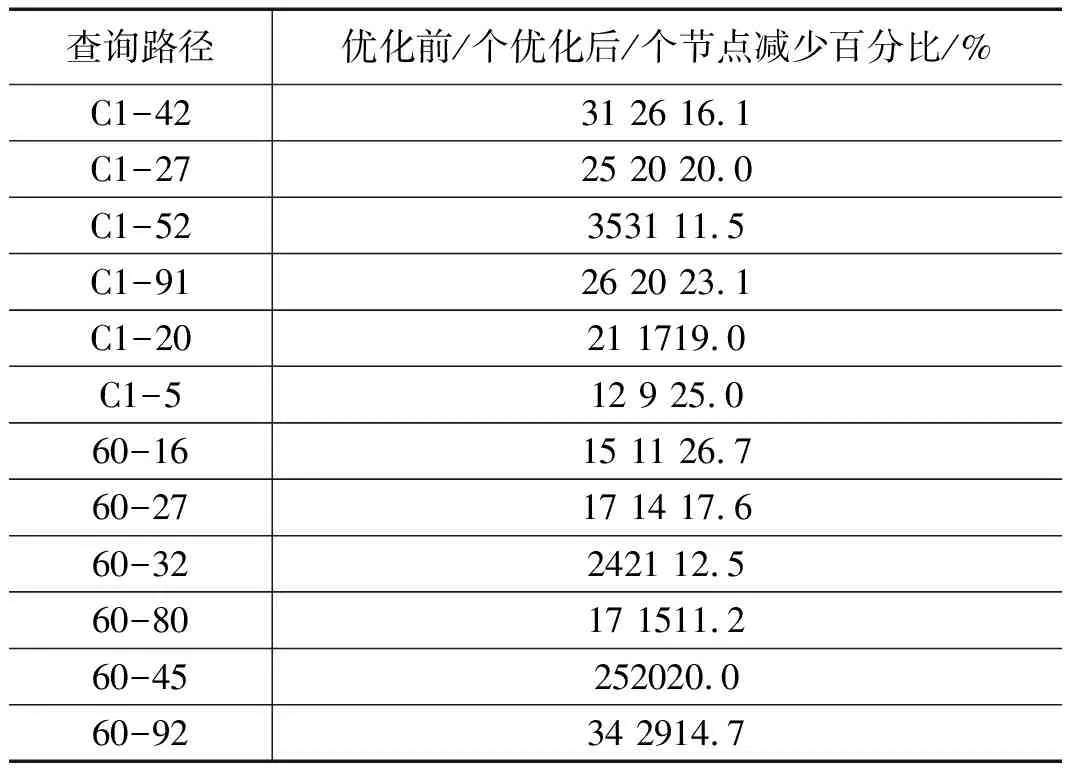
表3 A*算法优化前与优化后的遍历节点数比较

在停车场动态泊车时，停车场的繁忙程度决定着车位占用概率即m值的大小，结合实际停车情况，本文分别取表征不同停车繁忙程度的m值为2/3和1/2来验证泊车成功概率，从上表1、2的横向对比实验数据看出，优化后的A*算法在动态泊车路径规划中的应用大大提高了泊车成功概率，且随着m取值的增大泊车成功概率提升幅度亦增大，表明优化后的A*算法对解决停车高峰期动态泊车问题的优化效果更加明显，从而提高了车位的利用率以及减少了用户的泊车时间。而从表3看出，相比于Dijkstra 算法的全节点遍历，A*算法的遍历节点最多为35个约等于总节点数的1/3。从图3的动态路径规划示意图可知，矩形区域中有37、42等多个可用空车位节点，结合空车位的密集分布特性，文中采用最小x坐标的42号节点作为动态路径规划的目标节点进一步减少了遍历节点的总数，很大程度的提高了算法的运行效率。

5 结语

本文从实际停车问题出发，结合停车效率以及路径规划提出了泊车成功概率概念，以泊车成功概率和算法搜索效率为主要评价指标，通过矩形限定区域约束法对A*算法进行优化，将动态泊车导致的停车效率问题转化为泊车概率问题，围绕车位实时变化情况下的动态路径规划问题展开研究。实验结果显示，优化后的算法提高了泊车成功概率和算法运行效率，这将大大减少用户在停车高峰期不断盲目寻找车位的时间，保证泊车用户能够以最短的规划路径且较高的泊车概率进行泊车，进而提高停车用户的停车体验以及停车位的利用率，具有一定的实用研究价值。但此算法仍有一定的缺点，由于空车位的随机分布性，泊车成功概率较高的目标区域距离初始节点的路径花费有可能较高，泊车成功概率与路径花费的权衡可以作为A*算法在停车场动态泊车应用中的一个研究方向。