基于核空间与稠密水平条带特征的行人再识别

，，，，

(浙江理工大学 信息学院, 杭州 310018)

0 引言

行人再识别指的是在非重叠视域多摄像机监控系统中, 匹配不同监控画面中的目标行人。行人再识别在目前的视频监控中有着许多重要的应用，比如行人检索[1]、多摄像机行人跟踪[2]和行为分析。行人再识别技术节省了从海量的图片和视频中搜索目标行人所带来的人力开销。但由于在不同的摄像机场景中，行人图像受到光照、视角和行人姿态等变化的影响，在监控画面中容易形成较大的外观差异，使得行人再识别问题遇到了很大的挑战。为了应对这些挑战，研究人员主要从两个方面开展研究。一方面是寻找鲁棒的行人特征描述，另一方面是学习有效的度量学习方法。

鲁棒的行人特征描述其最主要的是设计对不同行人图像具有区分性和对视角、光照、背景的变化具有鲁棒性的描述特征。许多已经存在的行人再识别算法试图通过建立一个特有的，健壮的代表特征来描述在各种变化环境下的行人外观。文献[3]利用人体的结构信息，在人体不同区域提取空间直方图和区域协方差特征。文献[4]也提出了类似的方法，对人体部件区分对待，将行人图像分割为头、躯干和腿，再分别提取各部分的颜色直方图、最大稳定颜色和重复纹理特征。最近，显著性信息也出现在行人再识别上的应用研究，文献[5]采用4种方向显著性加权融合学习的方法来度量一对行人图像的相似度。

除了有代表性的特征外，距离度量学习也是行人再识别的另一个研究方面。文献[6]提出了一种叫KISSME(Keep It Simple And Straightforward Metric)的度量学习算法，该算法将样本特征之间的差向量看作是高斯分布中的一个点，同类样本特征的差向量分布在同一个高斯分布中，而不同样本特征之间的差向量分布在另一个高斯分布中，然后用概率的比值来度量样本之间的距离。文献[7]提出了一种名为PCCA(Pairwise Constrained Component Analysis)的新方法，用于在高维输入空间中从稀疏成对相似/不相似约束学习距离度量，并学习投影到低维空间。然而，这种方法容易过度拟合。在文献[8]中，提出了正则化的PCCA(rPCCA)方法来改进PCCA，通过引入一个正则项来解决这个问题，该正则项使用可得到的附加自由度来最大化类间的边界。文献[9]提出一种名为XQDA(Cross-view Quadratic Discriminant Analysis)的度量算法，该算法在跨视角的训练样本的子空间中用二次线性判别分析方法得到一个度量函数用于跨视角样本的相似度计算。但是文献[9]中直接在原始线性特征子空间中训练得到的相似度度量矩阵，进而得到表示样本之间相似度函数。考虑到原始特征子空间线性不可分的性质，因此通过原始特征子空间直接训练得到的相似度度量矩阵不能准确的描述样本之间的相似性和差异性。

本文提出了一种在核空间学习稠密水平条带特征的度量学习算法。首先，在稠密的水平条带上提取特征，将所有水平条带上的特征串联得到行人特征；然后，通过相应的核函数将原始线性特征映射到非线性核空间中；最后，在核空间中学习得到一个对背景、视角、姿势变化具有鲁棒性的相似度函数。

1 相似度度量函数的学习

1.1 XQDA度量学习算法

文献[9]中提出了一种XQDA的算法，该算法是在Bayesian Face[10]算法和KISSME算法的基础上延伸得到的一种跨视角度量学习方法。度量一对行人的相似度可以表示为式(1)。

(1)

其中，xi,xj分别表示第i个样本和第j个样本的特征向量。同类样本之间的特征向量之差可以表示为ΩI，不同类样本之间的特征向量之差可以表示为ΩE。∑I和∑E分别是ΩI和ΩE的协方差矩阵。

文中利用线性判别分析的方法学习样本数据的子空间W=(w1,w2,…,wr)∈Rdxr，并且同时在r维子空间中学习相似性度量的距离函数。那么距离函数式(1)在r维子空间中可以表示为式(2)。

(2)

根据前面提到的ΩI和ΩE分别服从均值为0，协方差矩阵为∑I和∑E的正太分布，在子空间W中的映射σI和σE也有着均值为0，并且它们的值可以区别代表不同的两个类。因此我们可以在子空间W中用二次线性判别分析方法来优化学习下面的公式(3)来计算相似度。

(3)

其中，σE(W)=WT∑EW，σI(W)=WT∑IW，则式(3)可以表示为式(4)。

(4)

J的值越大，表示样本对(i，j)属于同一个行人的概率越大。

1.2 基于核空间的XQDA学习度量算法

原始特征空间中的特征向量xn通过核函数Φ映射到非线性核空间，则核空间中的特征向量表示为Φ(xn)。核函数映射的过程是求解原始特征空间中的特性向量的内积，如式(5)所示。

k(x,y)=<Φ(x),Φ(y)>

(5)

其中，x，y∈Rd(d表示原始特征空间特征的维度)。把原始特征空间中任一特征向量xp映射到易区分的非线性核空间中得到非线性特征向量kp，如式(6)所示。

kp=[k(x1,xp),k(x2,xp,...,k(xn,xp))]

(6)

(7)

上述流程首先将原始线性特征空间中任一个特征向量xn通过核函数k映射到易区分的非线性核空间中得到非线性特征向量kp，然后在非线性特征的子空间学习得到相似度度量矩阵。在这里常用的核函数有线性核函数、径向基核函数和二次有理核函数。经过后面的实验比较结果验证，本文算法采用径向基核函数。

2 行人图像的特征表示

行人图像特征的描述是行人再识别算法中的一个重要环节，本文采用HSV、YCbCr和Lab三种颜色空间的颜色直方图和SILTP[11](scale invariant local ternary pattern)纹理直方图来描述一张行人图像。每种颜色空间都有各自的颜色描述体系，所以对同一张行人图像的颜色特征描述的侧重点也各不相同。SILTP是著名的LBP(local binary pattern)纹理描述算子的改进算法，LBP算法的缺点是对图像噪声比较敏感，所以SILTP算法还结合了LTP(local ternary patterns)算法取得了对图像噪声和光照变化具有更强的鲁棒性。

我们把一张行人图像归一化为128×48像素，相同行人的目标图像，对应的局部区域在图像的垂直方向上是不会发生较大的变化，不过在实际中行人目标由于姿态和视角的变化可能存在轻微的高度变化。因此，用一个大小为10×48像素大小的矩形作为滑动的水平条带去描述行人图像水平方向的局部细节，水平条带的滑动方向自顶向下，每次滑动的步长为5个像素。在每个水平条带中，分别提取HSV、YCbCr和Lab三种颜色空间中每个通道的颜色直方图和SILTP纹理直方图。这样得到的直方图特征不但对行人图像视角变化具有很好的鲁棒性，而且可以捕捉到行人图像的局部细节特征。图1显示滑动水平条带提取特征的过程。

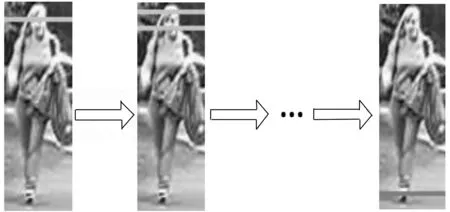
图1 滑动水平条带提取特征示意图

在提取特征的过程，我们考虑到了行人图像的多尺度信息。在不同的图像尺度上，有着不同的图像信息。因此在原始图像128×48像素的基础上进行两次金字塔降采样分别获得64×24像素的尺度图像和32×12像素的尺度图像。在每个尺度上的行人图像重复上述的特征提取过程。最后我们把所有特征级联形成行人图像的特性描述，该特征的维数为9 000维(3*3*16维颜色特征+34维SILTP纹理特征)*(24+11+5水平组)。

不同摄像机中行人视角的变化主要集中在水平方向上，而在垂直方向上并不很明显。因此，该文提取的特征对于水平方向的移动具有一定的不变性。

3 实验结果及分析

本文算法分别在VIPeR[12]数据集和iLIDS[13]数据集上进行大量的实验测试。算法性能的评价准则采用累积匹配特征(Cumulative match characteristic, CMC)曲线来评价算法的性能。给定一个目标行人图像查询库和行人图像候选库，累积匹配特征曲线描述的是在行人图像候选库中搜索待查询的目标行人，前r个搜索结果中包含正确匹配结果的比率。其中，第一匹配率(Rank=1)为真正的识别能力，所以比较重要。但是当Rank值较小时，也是可以通过人眼进行辅助识别查找目标，因此也具有现实意义。实验中，随机选择t对行人图像对作为训练集，余下的行人图像对作为测试集。相机A中的行人图像作为查询目标库，相机B中的行人图像作为候选目标库。每对行人图像，任意选择一张图像加入查询目标库，另一张则加入候选目标库。每个查询目标库与候选目标库中的每张行人图像都要有匹配。为了得到稳定的实验结果，以上过程重复10次，并将10次实验的平均值作为最终的实验结果。

3.1 VIPeR数据集的实验结果

VIPeR数据集是行人再识别领域最常用的且最具有挑战性的数据集之一。它包含了632对行人图像，每对行人图像都是由两个不重叠视角的摄像机在不同的室外环境下获取的。在632对行人图像中存在着许多视角，亮度，背景有着较大变化的图像对。

实验中测试样本集和训练样本集均为316对行人图像。VIPeR数据集上的其他实验，如果没有明确说明测试集和训练集的个数，则都默认为316对行人图像。为了对比本文算法基于不同核函数的算法性能，实验中其他条件都一样。表1给出了该算法基于不同核函数的实验对比结果。

表1 本文算法基于不同核函数的实验结果

从表1可知，本文算法基于径向基核函数的效果最优。为了充分体现本文算法的效果，在后面的实验效果对比中都是基于径向基核函数。图2给出了本文算法与已有行人再识别算法的性能比较的CMC曲线，表2是对应的实验结果的数据。

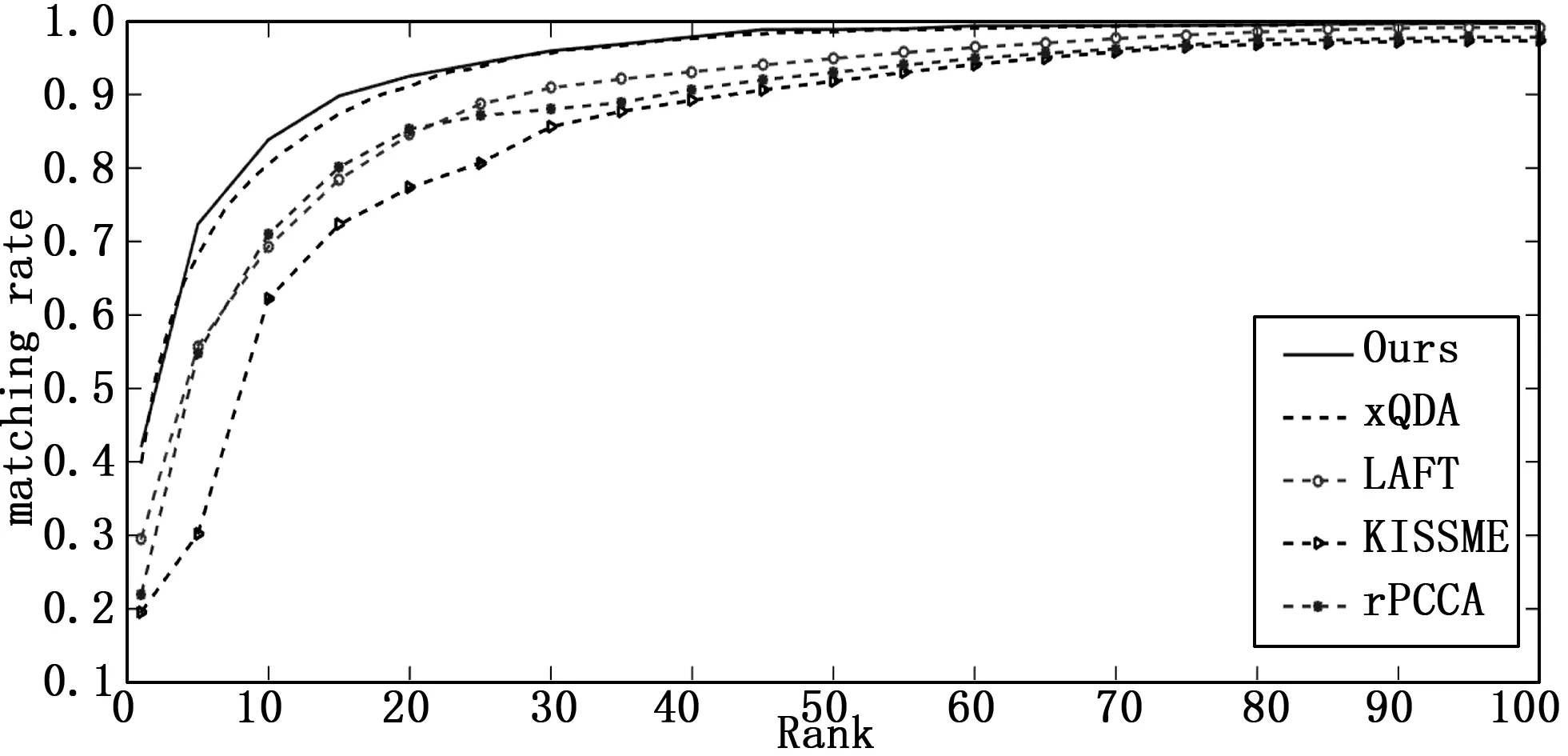
图2 VIPeR数据集上本文算法与已有算法性能对比实验结果

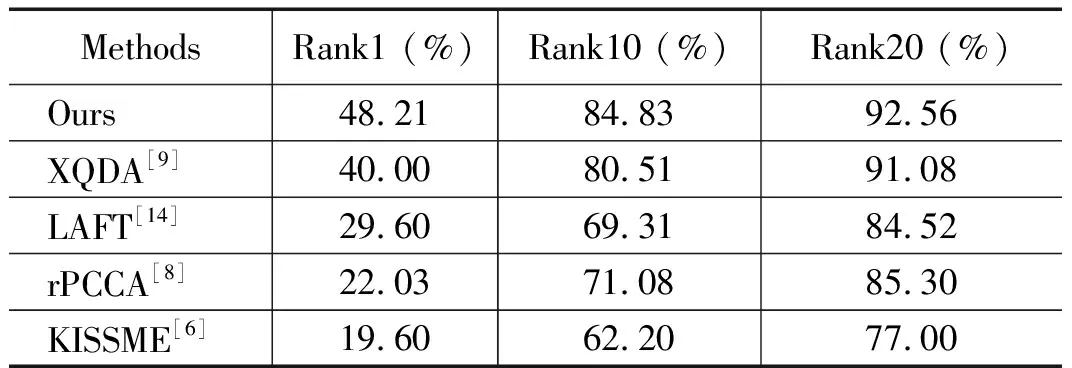
表2 VIPeR数据集上本文算法与已有算法性能对比实验结果(训练集样本规模t=316对图像)

从图2和表2可知，本文算法性能有较大的提升，尤其是Rank1比表中排第二的XQDA算法提升了约8.2%，并且在Rank20内都有着较高的识别率。在一定程度上，本文算法的效果已经能够应用到工程实践中，尤其是在刑事侦查等方面，刑侦人员可以在行人再识别返回的前r个结果中快速搜索出目标行人，大大提高侦查办案效率。

当训练集规模为t=200时，本文算法与已有算法的性能对比结果如表3。

表3 VIPeR数据集上本文算法与已有算法性能对比实验结果(训练集样本规模t=200对图像)

从表3中可知，在只有少量训练样本情况下，本文算法同样优于已有算法。由此可见，本文算法有效的解决了学习相似度度量函数中出现过拟合的问题。

为了说明本文算法的优越性，表4给出了本文算法仅用一种特征情况下与其他算法效果对比。由于表中对比的算法都有HSV颜色空间特征和LBP纹理特征，因此实验中分别选用HSV和LBP作为本文算法提取的特征。

由表4可知，该算法虽然只使用了一种特征，但是效果比其他采用多特征的算法更好。其中，KISSME算法融合了HSV、Lab和LBP等特征，Rank1仅有19.6%。而本文算法只用了HSV颜色特征，Rank1就达到了41.6%。当本文算法用到多特征时，算法的识别率又提升了一些，但是继续增加特征，算法识别率提升的幅度会越来越小，而算法的时间复杂度会越来越高。因此，本文算法在最终的特征选择上只选用了三种颜色空间特征和一种纹理特征。

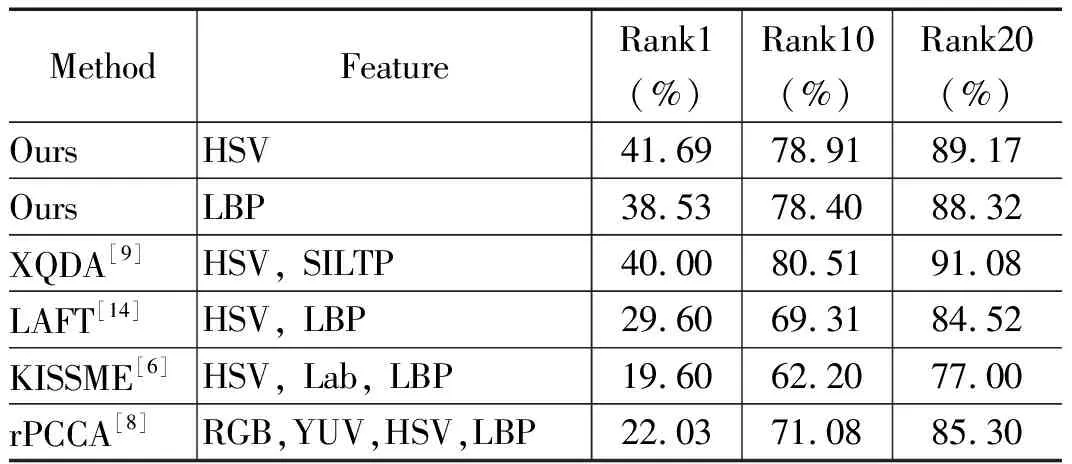
表4 仅用一种特征情况下的本文算法与已有算法性能比较实验结果

3.2 iLIDS数据集的实验结果

iLIDS数据集是在候机大厅中人群密集的场景下采集的。该数据集包含476张图像，图像全部来源于119个行人，其中每个行人的图像从两张到八张不等。该数据集里的行人图像有严重的遮挡和光照变化等问题。实验中对每个行人随机选择两幅图像，这样得到一个具有119对行人图像库。由于iLIDS数据集中图像的尺寸大小不一，所以我们统一把图片的尺寸设置为128×48像素。随机选择59对行人图像作为训练样本集，剩下60对行人图像作为测试样本集。表5给出了本文算法与已有行人再识别算法的性能比较。

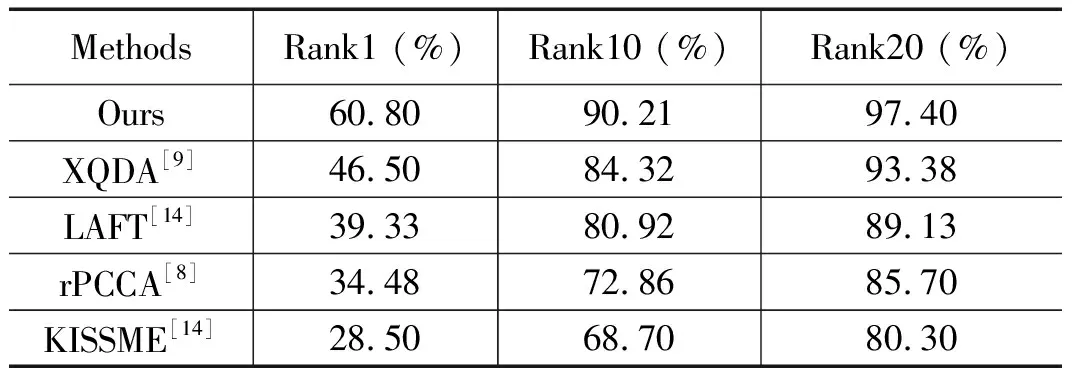
表5 iLIDS数据集上本文算法与已有算法性能对比实验结果

从表5中数据可知，在iLIDS数据集里，本文算法性能明显优于表中的其他算法。其中本文算法的Rank1达到了60.8%，比表中排第二的XQDA算法提升了约14%，Rank10至Rank20也有明显的提升，证明了本文算法的优越性。

4 结论

近几年，行人再识别技术的研究面临着许多问题。在不同摄像机视域下，行人图像的光照、视角和姿态等情况会有所变化，这是研究行人再识别过程中比较棘手的几个问题。目前，基于度量学习的行人再识别算法一般是在原始特征空间学习得到相似度度量矩阵，考虑到原始特征子空间线性不可分的性质，因此通过原始特征子空间直接训练得到的相似度度量矩阵不能准确的描述样本之间的相似性和差异性。，从而导致识别效果较差。对此本文提出了一种在核空间学习稠密水平条带特征的行人再识别算法。由行人再识别的公共数据集VIPeR和iLIDS上的实验结果表明，基于本文算法学习得到有效的相似度函数，识别性能优于已有的行人再识别算法。但本文算法在在行人遮挡较严重时，会因丢失部分行人特征信息而使识别率下降的情况。因此在接下来的工作中将会针对行人遮挡较严重的情况下做进一步研究。