基于GA-LM-BP神经网络的锂离子电池预测研究
,
(海军工程大学 电子工程学院,武汉 430033)
0 引言
锂离子电池具有效率高、放电量少以及自适应性强等优势,目前在电动汽车、新能源发电和储能电站等领域得到了广泛的应用,如何对锂离子电池进行预测已经成为当前电子设备PHM的关键方面。通过分析锂离子电池的状态退化的机理,得到对锂离子电池进行预测的依据。本文针对对传统BP算法的不足,本文采用遗传算法优化网络初始的权值阈值及LM算法的改进型BP神经网络,并应用于锂离子电池的预测研究中。
1 锂离子电池状态退化机理
锂离子电池在结构上可以分为正极、负极和电解质。其中,电解液通常是有机碳酸酯,负极材料是石墨,正极材料是锂铁磷酸盐。锂离子电池的正负极在充放电的过程中进行接收和释放锂离子,并完成相应的能量转换。锂离子的充放电化学反应公式是:
充电过程:正极反应公式:LiFePO4→Li1-xFePO4+xLi++xe-
负极反应公式:xLi++xe-+ 6C→LixC6
放电过程:正极反应公式:Li1-xFePO4+xLi++xe-→LiFePO4
负极反应公式:LixC6→xLi++xe-+ 6C
充电时,电池是将电能转换成化学能,而放电时将化学能转换成电能[1]。在锂离子电池的充放电过程中,内部发生了不可逆的化学反应,从而导致电极上的Li+的流失,使内部电阻提高。这些内部电阻的变化就是反映电池性能退化的主要参数。
实现锂离子电池RUL预测的重要环节就是建立其寿命退化模型。但是在实际应用中能够比较准确的建立电池退化的物理模型是困难的。NASA的PCoE研究中心依据大量的实验数据[2],提出了一个简单可行的电池等效模型,并以此来估计锂离子电池的RUL,等效模型如图1所示。
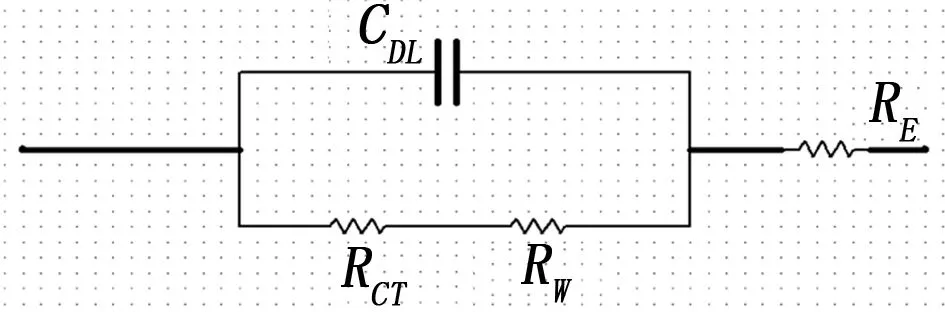
图1 等效模型
其中:CDL表示双电层电容,RCT表示电荷转移电阻,RW表示Warburg阻抗和RE表示电解质电阻。NASA的研究人员对数据分析后发现,RW和CDL对寿命退化所起的作用微不足道,可以忽略,而与RCT+RE成高度的线性关系,并验证了锂离子电池容量和阻抗参数之间成高度的线性相关性。Saha等人提出了如下的经验模型来描述锂离子电池[3]。
Ck+1=ηCCk+β1exp(-β2/Δtk)
(1)
其中:Ck是第k个循环周期的锂离子电池容量,Δtk是两个相邻充放电周期之间的休息时间,β1和β2是电池经验模型的特定参数。ηC是库仑效率,用来表示电池释放的电荷总量与冲入电荷总量之间的百分比。在锂离子电池中,充放电后增加电池的休息时间,就能够使下一次充电周期的电池容量有所增加。
由以上分析不难看出,电池容量会随着锂离子电池的老化而逐渐降低,每次充电的电池容量基本上是逐步远离标称容量的,所以可以利用锂离子电池容量退化来预测剩余寿命。
实验数据来源于美国马里兰大学CACLE开展的锂离子电池退化实验。在实验中,采用的是Arbin BT2000的锂电池实验系统,并以Excel格式保存电池退化的数据,共有两组锂离子电池数据,标准容量分别是1.35 Ah和1.1 Ah。本文采用容量是1.1 Ah的测试数据。整个实验数据在构成上主要是由充电、放电和电池容量等部分,其中充电实验数据包含阻抗数据、充电电压数据和充电电流数据,放电实验数据包含阻抗数据、放电电压数据和放电电流数据,以及相应的环境温度、测试时间等信息。
针对传统BP算法的不足,采用遗传算法优化网络初始的权值阈值及LM算法的改进型BP神经网络,并应用于锂离子电池的预测研究中。
2 GA-LM-BP神经网络建模
BP神经网络的误差后向传播过程是通过一个目标函数最小化完成的,而目标函数是:
(2)
传统上是根据如式(2)的梯度下降法来调整权重系数的。
(3)
权值会顺着与误差梯度相反的方向变化,直到误差达到最小值。这种BP神经网络的训练时间较长,迭代次数也比较多,具有陷入局部最小值的缺点[4]。针对上述问题,本文采用LM算法对网络进行训练,并克服这些缺陷。
2.1 LM-BP神经网络建模
LM(Levemberg Marquardt,LM)算法是了融合高斯-牛顿法和梯度下降法优点的快速算法,既具有快速收敛特性,又具有全局搜索的优势[5]。假设使用ω(k)表示第k次迭代的权值形成的向量,那么新的向量ω(k+1)由下式可以得到:
ω(k+1)=ω(k)+Δω
(4)
神经网络的输入误差指标函数E(ω)表示如下,
(5)
接着,通过最小二乘法求解BP神经网络的误差函数得到调整规则是:
Δ(ω)=-[▽2E(ω)]-1▽(ω)
(6)
▽2E(ω)是输入误差E(ω)的Hessian矩阵,E(ω)是梯度,针对▽2E(ω)进行近似推导,可以得到,
▽(ω)=JΤ(n)e(n)
(7)
▽E2(ω)=JΤ(n)e(n)+S(n)
(8)
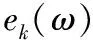
(9)
(10)
其中,修正为高斯—牛顿法是:
Δ(ω)=-[JT(n)J(n)]-1J(n)e(n)
(11)
LM算法可以将高斯—牛顿法改进如下,
Δ(ω)=-[JT(n)J(n)+μI]-1J(n)e(n)
(12)
其中:I是单位矩阵,μ是比例系数,而且大于零。当距离一个解值比较近时,μ值是逐渐递减的,权值调整与高斯—牛顿法相似;当距离一个解值比较远时,μ值是逐渐增加的,权值调整与梯度下降法相似。其的下降速度比梯度法要快很多,并且经实验证明,下降速度比梯度法提高了几十到一百倍,极大地改善了神经网络的性能[6]。
LM-BP神经网络的模型实现步骤如下:
1)首先是确定LM—BP神经网络的训练误差允许值ε,系数β,初始权值μ和阈值ω(0),并令,μ=μ0,k=0;
2)对LM-BP神经网络的输出进行计算;
4)按照式(11)和式(4)计算Δω和E(ω(k));
5)如果E(ω(k))>ε,按ω(k+1)作为权值和阈值计算误差函数E(ω(k+1));否则结束计算。
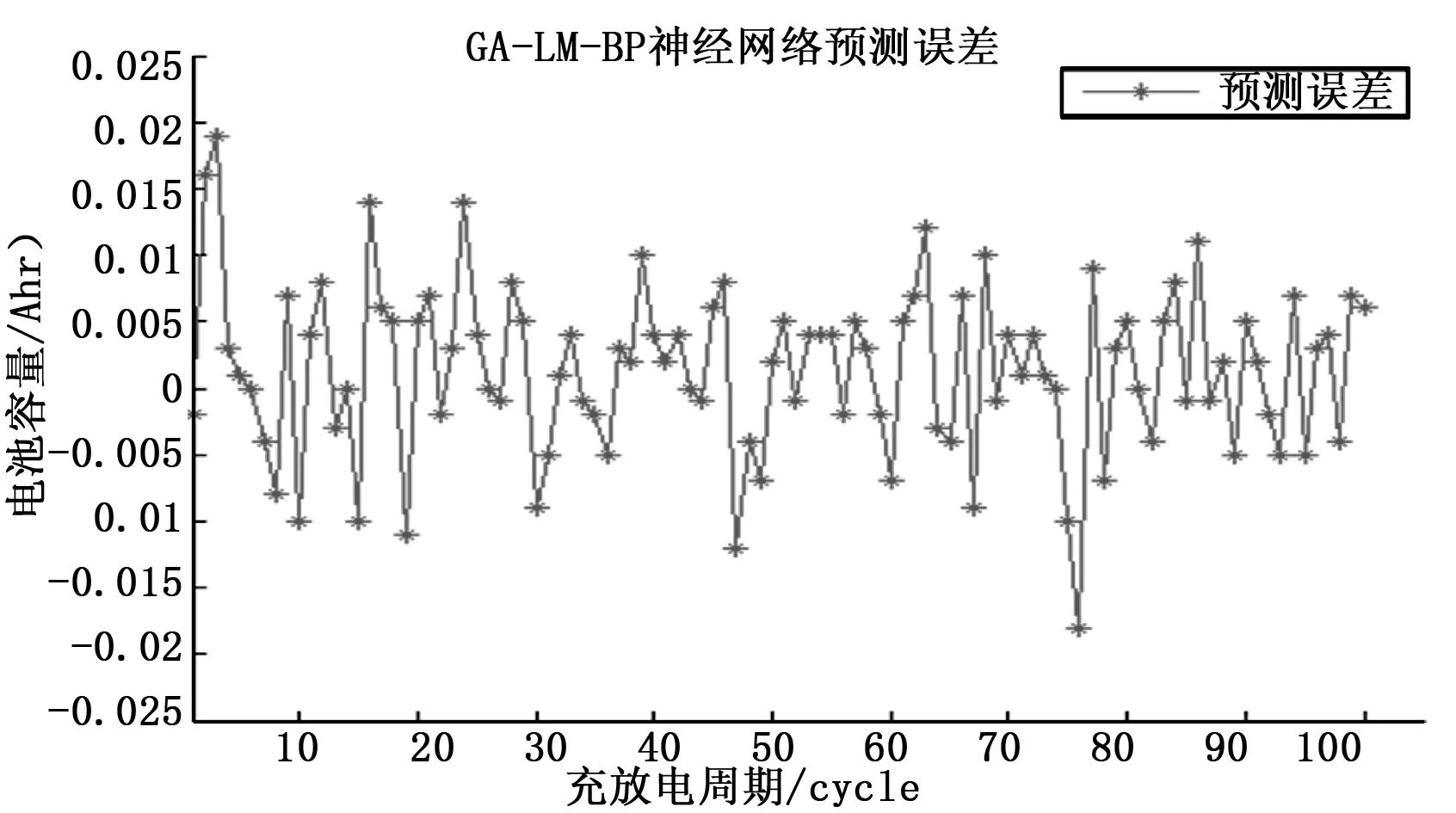
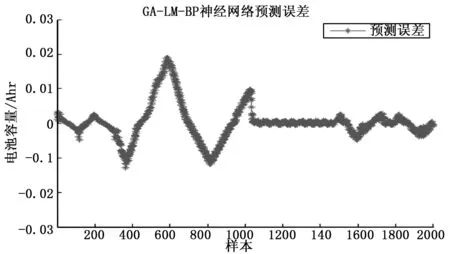
6)如果E(ω(k+1)) 7)结束计算。 BP神经网络的权值和阈值一般是在[-0.5 0.5]之间的随机数,但是这些参数对神经网络的训练效果影响很大,而且是无法准确获取[7]。针对这个问题,本文采用GA优化来得到最佳的初始权值和阈值。GA是利用自然界中适者生存的选择原理,是一种面向全局的优化搜索人工智能算法,且具有鲁棒性强的优势[8]。 GA优化LM-BP网络主要分为三部分:网络拓扑结构的确定、GA优化初始权值和阈值、更新权值和阈值后的网络进行预测。具体的实现流程如图2所示。 图2 GA优化LM—BP神经网络流程 步骤1:确定LM-BP神经网络拓扑结构。一旦确定LM-BP神经网络络的拓扑结构(三层网络结构应用的比较多),初始权值和阈值也就确定了。 步骤2:种群初始化。任意产生LM-BP神经网络的初始权值和阈值Xi=(ωmi,ωip,ai,bp),其中m,i,p分别是三层网络的节点数,创建初始种群PX={X1,X2,…,Xn},n是种群大小,然后使用实数对种群个体进行编码。 步骤3:将LM-BP神经网络训练的误差定义为适应度函数F,染色体的适应度越小,其成为下一代的概率就越大。 (13) 其中:dp是GA-LM-BP在p节点的理想值;yp是GA-LM-BP在p节点的预测值;k表示系数,取值区间是[0,1]。 步骤4:选择操作。利用轮盘赌法形成“交配池”。这样,个体被选择的概率和适应度大小就是成正比的,形式如下: (14) 步骤5:从上面的“交配池”中选择任意两个染色体进行交叉操作。通过比较父、子染色体适应度函数的大小。如果求得的适应度是减少的,则继续保留父染色体,否则就用子染色体替换父染色体。 步骤6:从“交配池”中以相应的概率任意选择一个染色体进行变异操作,生成子染色体。如果子染色体的适应度大于父染色体,则保留子染色体。否则就是保留父染色体。 步骤7:一旦迭代次数达到最大值,就得到最优权值和阈值,否则跳转到步骤3,继续进行优化。 步骤8:采用上面GA优化得到权值和阈值参数对网络的训练样本进行学习,从而得到LM-BP神经网络预测模型。 步骤9:将测试样本集输入到LM-BP神经网络预测模型,对预测准确率进行验证,预测准确率达到要求就结束,否则跳到步骤1进行重复执行。 依据Kolmgorov定理,三层的BP网络就能够满足所有精确性要求实现对连续函数数值逼近[9],本文采取三层网络拓扑结构对锂离子电池的容量进行预测。测试数据采用马里兰大学CACLE的锂离子电池数据,测试数据中包含充/放电压、充/放电流、阻抗、温度和测试时间等信息,这些测试数据都会明显影响到电池的容量。所以把他们都作为神经网络的输入变量。需要预测的电池容量作为的BP神经网络的输出变量。采用黄金优选方法来确定中间隐含层的神经元节点数。BP网络的输入层节点数是m,输出层节点数目是p,则理想的隐含层节点数目i的取值范围是: (5+1+10)=16=b (15) 根据上述分析,确定BP神经网络如图3所示的5-6-1三层结构。 图3 BP神经网络拓扑结构 使用该BP神经网络结构,根据上述的拓扑结构的计算方法,不难得到共有42个权值和阈值,在后续GA的个体编码长度就是42,其中输入层到隐含层是30位,隐含层是6位,隐含层到输出层是6位,输出层数1位,如表1所示,并采用实数对个体进行编码。 表1 初始权值和阈值位数 采用的是Arbin BT2000的锂电池实验系统,并以Excel格式保存电池退化的数据,本文主要是采用容量是1.1 Ah锂离子电池的数据进行训练和测试。 针对三层BP网络的参数进行100次调试,确定迭代次数是100,学习率是0.1,训练目标是0.004%。针对测试数据进行滤波处理,滤除噪声信号,并进行归一化处理。随机选取2000组数据,1900组作为训练数据,用于网络训练,100组作为测试数据,按照设计要求构建BP神经网络预测模型,用于样本的训练学习。再将测试集输入到BP神经网络模型,对输出值进行预测,对于选择的测试数据集,BP神经网络的预测误差如图4所示。 图4 BP神经网络预测误差 由图4不难看出, BP神经网络的整体输出结果还是比较不错的,但是还是存在一定的预测误差,主要是是集中在预测的刚开始阶段,此时主要是用于训练学习的,而且误差还是有点大,最大达到了0.029 7;而到了中后期误差会小很多。 图5 BP神经网络样本预测误差 由图5不难看出,按照给定的BP神经网络结构对训练样本进行学习,整体的预测效果还是不错的,最高误差是0.03。在训练样本数达到1200个以后,预测误差越来越小,并且比较稳定,波动性很小,这就体现出BP神经网络的优势。 针对BP神经网络误差大的缺点,引入前面GA优化LM-BP神经网络进行状态预测。首先确定BP神经网络是5-6-1的三层网络结构,GA个体的编码长度是42位,GA的进化代数是50,种群规模大小是30,采用轮盘赌法交叉操作,交叉概率是0.8,变异概率是0.01,适应度函数是BP网络的预测误差F。按照GA-LM-BP神经网络的建模步骤进行训练学习,GA优化过程中的适应度函数的变化值曲线是随着代数的增加而下降的。如图6所示,表明预测误差越来越小,并且经过50代进化后得到的最优权值和阈值如表2所示。 图6 适应度变化曲线 表2 最优初始权值和阈值 将表2中的最优权值和阈值赋值给BP神经网络,再利用优化后的网络进行训练,并预测整个系统的输出,就可以得到GA-LM-BP网络预测的输出,GA-LM-BP网络预测误差如图7所示。 图7 GA-LM-BP网络预测误差 由图7不难看出,GA-LM-BP神经网络在非线性函数的拟合上比BP神经网络的能力更强,预测误差明显减少,精度提高。 图8 GA-LM-BP神经网络的输出预测误差 由图8不难看出,GA-LM-BP神经网络的输出预测效果更好,预测误差最高是0.019 5,平均误差是0.004 5。通过对比BP神经网络和GA-LM-BP神经网络的预测输出效果,使用了GA优化了初始权值和阈值后在预测结果方面更准确,稳定性提高,预测误差显著提高而且全局收敛性好,达到了比较理想的结果。 利用LM算法融合高斯-牛顿法和梯度下降法优点的快速性,并充分利用遗传算法全局随机搜索强的优势,构建了三层5-6-1型的GA-LM-BP神经网络结构,优化BP神经网络的初始权值和阀值,减少了BP神经网络陷入局部极小值的几率。对锂离子电池数据进行了实验表明,GA-LM-BP神经网络GA-LM-BP神经网络预测结果方面更准确,稳定性提高,预测误差显著提高而且全局收敛性好,实验结果验证了该方法预测的有效性。2.2 GA优化LM-BP神经网络建模
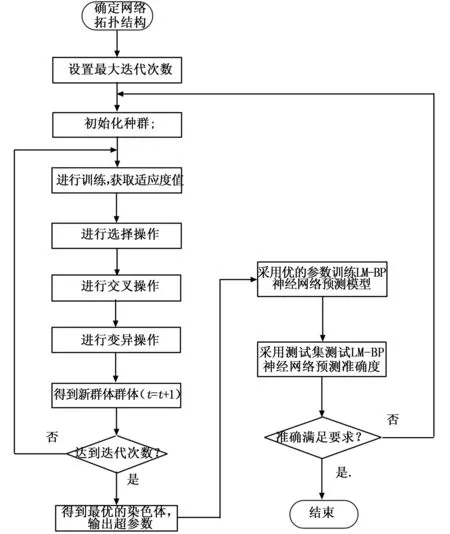
3 基于GA-LM-BP神经网络的锂离子电池状态预测
3.1 确定BP神经网络的拓扑结构
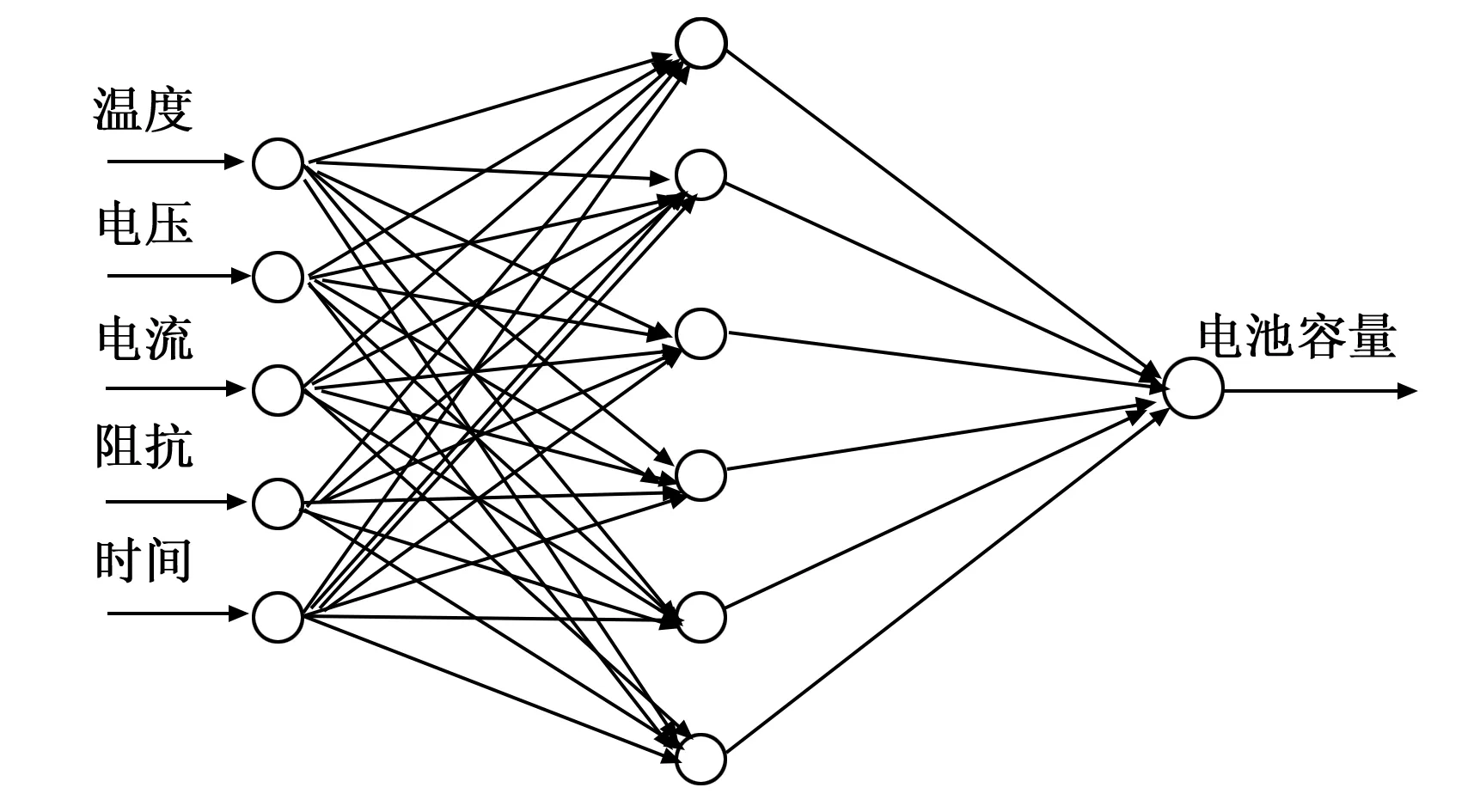

3.2 BP神经网络预测研究
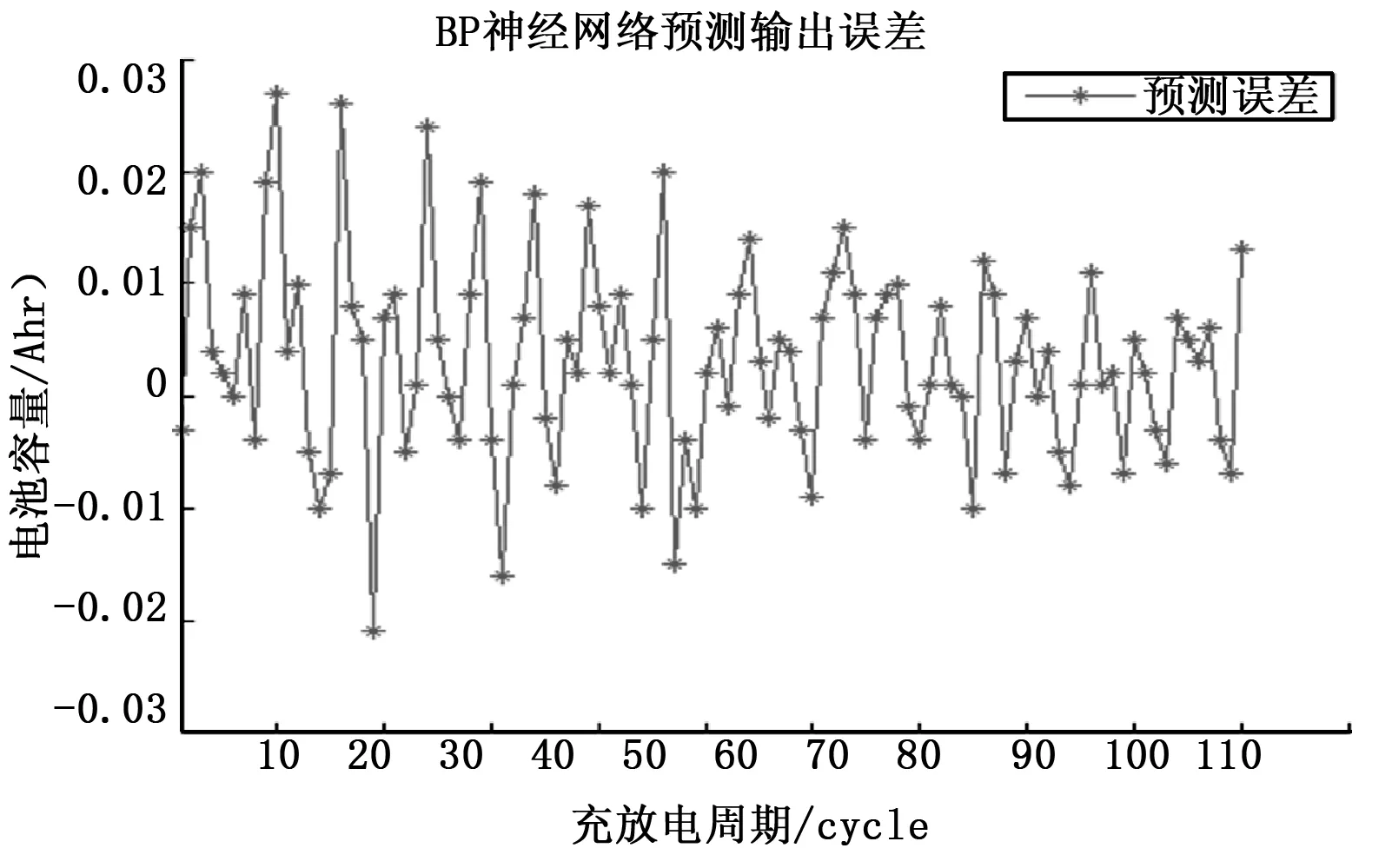
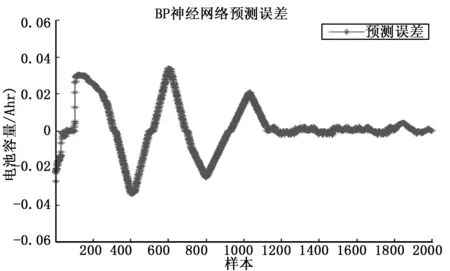
3.3 GA优化LM-BP神经网络的预测研究
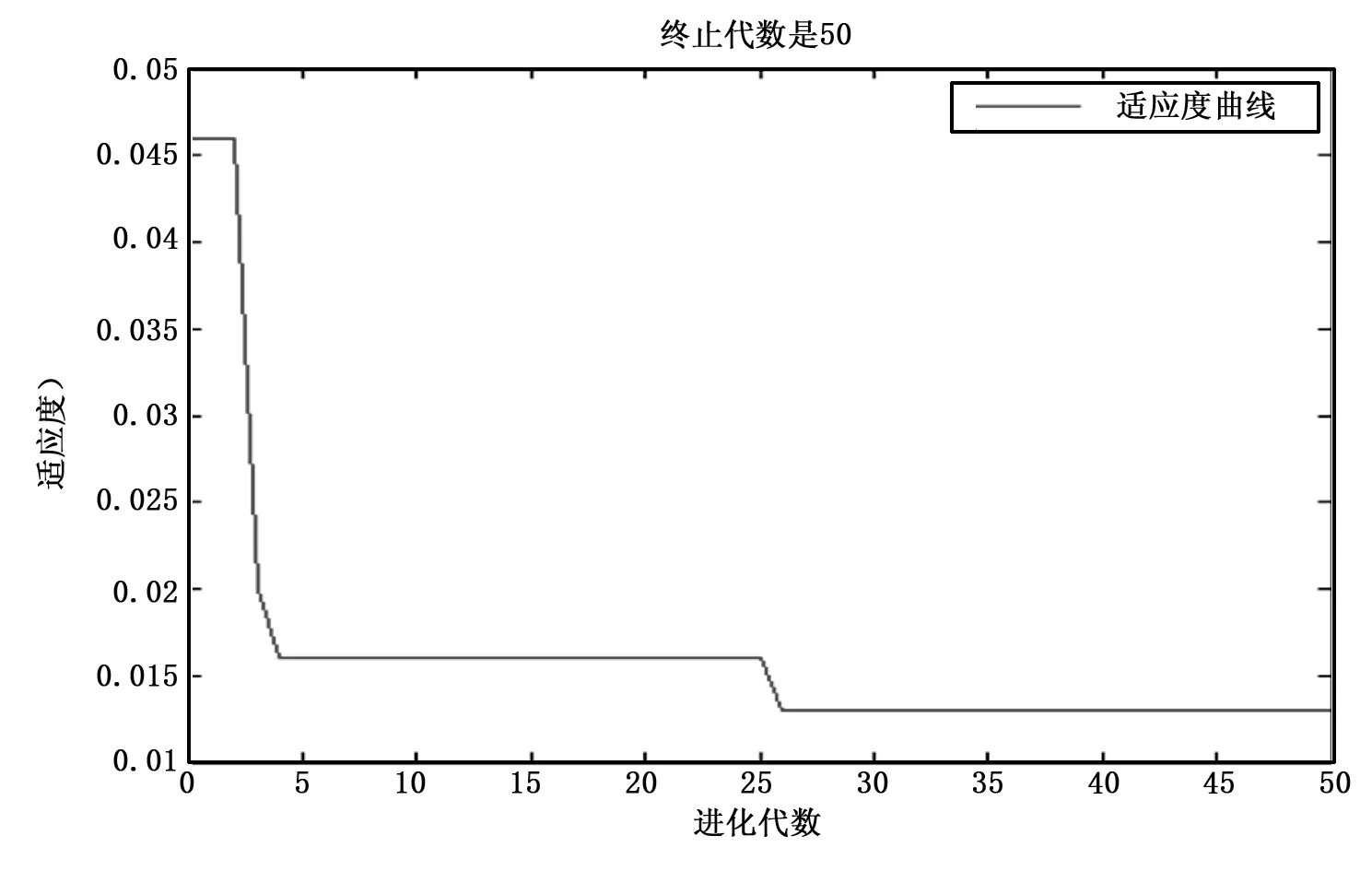
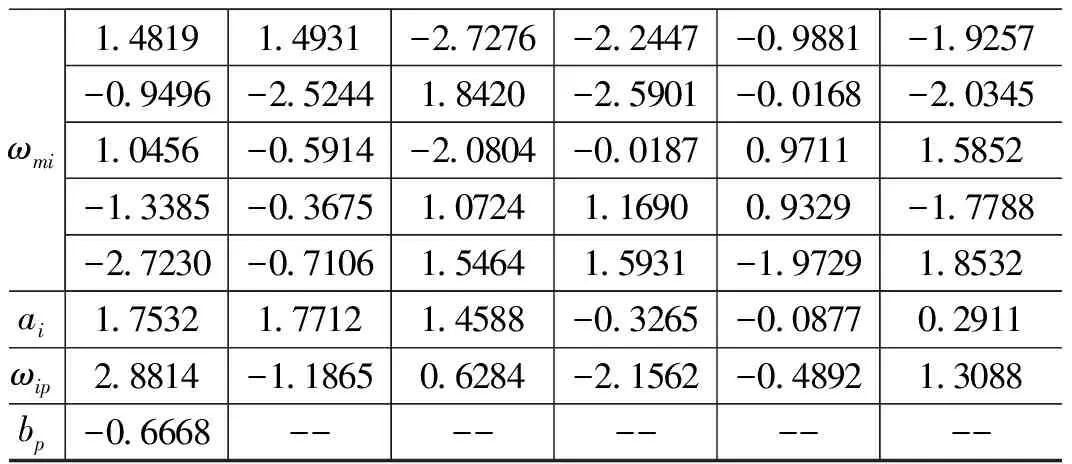
4 小结

