电网电压前馈对柔性直流输电在弱电网下的稳定性影响

郭 琦, 郭海平, 黄立滨

(1. 直流输电技术国家重点实验室(南方电网科学研究院有限责任公司), 广东省广州市510080;2. 中国南方电网公司电网仿真重点实验室, 广东省广州市 510663)

0 引言

近年来柔性直流输电技术快速发展[1],南方电网在广东南澳建设了世界首个多端柔性直流输电工程[2],在云南鲁西建设了世界首个常规直流和柔性直流并联运行的异步联网工程[3-4],国家电网也建设了舟山五端柔性直流、厦门柔性直流[5-6]、张北柔性直流[7]输电工程等极大地提升了中国柔性直流输电技术水平和装备制造水平。由于柔性直流输电采用模块化多电平换流器(MMC),在桥臂含有大量子模块的情况下,具有谐波小、无需考虑交流滤波器的特点[8-14],很少有文献分析其谐波特性,尤其是接入系统为弱交流电网情况下的高频谐波特性[15-17]。实际上,柔性直流输电接入弱交流系统运行时有可能出现高频谐波现象[15,18],本文以云南鲁西异步联网工程2017年4月10日发生的高频谐波谐振事件为例,分析了与高频谐波有关的各个因素,得出了MMC柔性直流电网电压前馈控制环节的不当设计是本次高频谐波谐振主因的结论,提出了在电压前馈控制环节增加滤波环节的高频谐波谐振解决方案,通过实时数字仿真仪(RTDS)仿真试验验证后在现场实施。

1 鲁西“4·10”高频谐波谐振现象

云南鲁西异步联网工程是世界上首个在主网采用柔性直流单元与常规直流单元并列运行进行背靠背联网的工程,其中柔性直流单元输送容量达1 000 MW,直流电压为±350 kV。

2017年4月10日,鲁西站常规直流单元处于停运状态,柔性直流单元单独运行,广西侧交流电网结构如图1所示。事件过程为:广西侧交流电网仅为一回出线(鲁西站到百色站的西百甲线),西马乙线由马窝站空充,广西侧交流系统容量非常低(鲁西站广西侧交流系统的等值三相短路容量小于3.3 GVA)。此时,鲁西站柔性直流单元、百色站、永安站等站点的交流电压电流均可观测到1 271 Hz左右的高频谐振,其中鲁西站网侧电压电流如图2所示。此时,降低柔性直流广西侧无功功率目标值或有功功率目标值,高频谐振电流基本保持不变。最终柔性直流单元跳闸,高频谐振随之平息。

图1 产生谐波时的电网局部接线图Fig.1 Partial wiring diagram of grid when harmonics are generated

以广西侧换流变网侧A相交流电压和交流电流为例,柔性直流单元停运前波形如图2所示,为MATLAB所画时域波形,录波软件分析截图见附录A图A1。

图2 鲁西站广西侧电压、电流及电压谐波Fig.2 Voltage, current and harmonics on Guangxi side

通过对高频谐振过程广西侧网侧相关波形现场录波进行傅里叶分析,发现本次系统产生的电压、电流高频谐振的频率主要为1 271 Hz。

2 高频谐波谐振的机理分析

柔性直流运行时高频谐波有关的因素包括:MMC柔性直流结构特性(如模块电平数[19])、阀控特性(包括子模块电容电压平衡和环流抑制策略[20])、锁相环控制、电压环控制和电流环控制等。由于本次高频谐波谐振的主导频率在1 kHz以上,锁相环控制的响应时间一般在100 ms左右[21],对高频谐波的影响不大。另外,柔性直流输送功率的大小理论上也会影响谐波[15,22],但是经对现场实际波形的分析发现,本次高频谐振事件中柔性直流功率的变化对谐振频率和幅值的影响均不大。因此,此次高频谐波谐振的最主要影响因素定位为柔性直流控制算法(包括电流内环控制和解耦控制部分[15,23]等)、MMC主回路阻抗特性及交流系统谐波阻抗特性,详细分析如下。

鲁西背靠背柔性直流单元的主要控制模式为云南侧控直流电压,广西侧控直流功率,柔性直流单元的控制周期为100 μs。广西侧功率控制的目标是控制向电网注入的电流,其中关键的电流环控制的控制可以简化表示,见图3。

图3 柔性直流电流环控制原理Fig.3 Control principle of flexible DC current loop

图3中iref为电流参考值;v为柔性直流输出电压;L为柔性直流的等值电抗;i为网侧电流;e为网侧电压;T2为电流环延时;T1为前馈电压控制环节的延时;Z(s)为交流电网的谐波内阻抗;s为控制参数;PI表示比例—积分控制器。

将图3的控制框图进行等效变换,得到控制框图如图4所示。

从图2的电流波形来看,电流振荡现象明显。而从图4可以看出,电网电压前馈环节相当于电流环的内环,由图4的控制框图可以推导出电压前馈环节的传递函数F为:

(1)

F的物理意义为电压前馈控制环节对交流电压的控制增益,包括幅值增益和相位偏移。F增益越大,电压前馈对电流环控制造成的扰动也越大,产生高频谐波谐振的可能性就越大。

式(1)中,将s=jω代入可得,当ω=n2π/T1(n=0,1,2,…,∞),此时(1-e-T1s)模值为极小值0;但是当ω=π/T1+(2nπ)/T1(n=0,1,2,…,∞),此时(1-e-T1s)模值为极大值2。

频率公式ω=2πf=2π/T,所以当谐波角频率满足ω=π/T1+(2nπ)/T1(n=0,1,2,…,∞)=2π/T时候,即谐波周期T=2T1/(2n+1)(n=0,1,2,…,∞)时,电压前馈环节会对该谐波信号进行2倍放大。这也就是说,前馈电压的延时T1,会导致f=(2n+1)/(2T1)(n=0,1,2,…,∞) 频率附近电网谐波阻抗的放大(即式(1)中F的增益会增大),这是本次谐波放大的主要原因。由后续的试验得出谐波主要产生在n=0的时候,即容易在f=1/(2T1)附近产生谐波谐振。

如果取消电网电压前馈控制的话,高频谐振出现的可能性就小很多。如果将交流电网侧等效为一个RLC并联等值回路(电容反映广西侧空充西百乙线的效应)。由此,根据高频谐波谐振发生时刻的交流电网等值为Z1(详细参数见附录A图A2),按照式(1)可画出加入电网电压前馈和不加前馈柔性直流系统对电网电压的影响传递函数F的波特图对比,如图5所示,图中A点表示系统为直接前馈,频率为1.15×103Hz,幅值为3.78 dB。

图5 有无电压前馈环节的波特图对比Fig.5 Comparison of Bode diagram with and without voltage feedforward

根据奈奎斯特稳定判据,由于电网电压前馈延时的存在,蓝色曲线在1 150 Hz和1 250 Hz左右对谐波起到了放大作用(对应此时的RTDS仿真结果,其谐波情况见图6和附录A图A3,主要为23次和25次谐波)。

图6 RTDS仿真复现谐波情况Fig.6 Harmonic by RTDS simulation

3 对机理分析的仿真验证

根据上述推导的式(1),柔性直流等效电抗的大小是固定的,因此高频谐波主要由式(1)中电网电压前馈环节的延时环节(1-e-T1s)及系统阻抗Z(s)来决定。根据奈奎斯特稳定判据,当Z(s)和(1-e-T1s)的幅值都很大的时候,就有可能产生高频谐波谐振。

本文仿真采用的试验平台为南方电网仿真重点实验室含鲁西柔性直流实际控制保护系统的闭环RTDS仿真平台,通过分别改变Z(s)和T1来验证原理分析的正确性。

3.1 延时T1固定,改变网络阻抗特性Z(s)

在鲁西柔性直流RTDS试验仿真系统中,由于前馈电压延时T1是由硬件本身特性决定的,为验证方便,首先通过改变电网等值谐波阻抗的方式来对上述原理进行验证。根据鲁西柔性直流广西侧电网接线结构,马窝站空冲西马乙线,线路中产生对地电容C,在RTDS中,可构造电网等值模型见图7。

图7 RTDS本次试验用柔性直流结构和电网模型Fig.7 RTDS simulation model of flexible DC structure and grid

改变图7中R1,R2,L1,C,L2等参数,就可以灵活地调节系统的阻抗,本文目前主要是通过调节C和R1,构造了4种不同的交流电网等值谐波阻抗网络,通过4种不同电网等值阻抗网络的RTDS试验,测量广西侧电网谐波的情况,阻抗网络参数及试验结果详见附录A。

可以看到,在Z1,Z2和Z3阻抗特性差别非常大的情况下,产生谐波的频率没有太大变化,主要还是在22次和23次左右,这也验证了式(1)中(1-e-T1s)项的作用,主要在f=1/(2T1)处产生谐波,反过来能推断动态性能测试系统(DPT)系统的前馈电压延时大概在434～454 μs之间。

在不同的电网谐波阻抗特性情况下,传递函数F的相角稳定裕度差别很大,当相角稳定裕度太小时,系统容易产生谐波谐振;当相角裕度为负时,系统必定产生谐波谐振(详见附录A)。

3.2 网络阻抗特性Z(s)固定,改变延时T1

由第2节的分析可知,系统容易在f=1/(2T1)处产生谐波,当增加前馈电压延时T1后,谐波谐振频率会降低。由于预估的前馈电压延时在434～454 μs,如果通过在RTDS模型的电压输出环节增加100 μs的延时,那么前馈电压控制环节的总延时将相应增至534～554 μs,原来22次和23次谐波将变为18次和19次谐波,原来对应的19次谐波谐振频率也会降低。通过RTDS仿真验证了上述推导,T1延时增大100 μs后,在不同电网阻抗特性下的试验结果如附录B所示。

本节通过不同的试验,分别独立地改变Z(s)和T1,证明了原因分析的正确性和准确性,即前馈环节延时T1主要影响产生谐波的中心频次f=1/(2T1),电网阻抗Z(s)的大小主要决定是否可能产生谐波谐振。

4 抑制谐波谐振的解决方案

由于谐波谐振的产生是由于控制系统中电压前馈环节的延时引起,不引入前馈环节而将前馈值固定是一种解决方案,但是这可能会对系统的抗扰动性能造成一定的影响。比如电网系统的电压往往不是额定的,那么固定值的前馈就有可能在固定前馈值附近解锁成功,但是实际运行时一旦电网电压偏离了固定值,则有可能过流导致解锁失败,低电压穿越、功率阶跃等动态特性都有可能受到影响。

本文提出的一种解决方案是将前馈电压进行恰当的滤波后再进行前馈,这样就能避免谐波谐振的产生,也能避免对系统动态特性造成大的影响。本文在RTDS送出到控制保护装置的电网电压中加二阶带通滤波器来实现,通带中心频率采用50 Hz,阻尼系数ξ分别为0.1, 0.707, 0.9时的频谱特性如图8所示。

图8 二阶带通滤波器设计Fig.8 Design of second order bandpass filter

5 解决方案的仿真验证和现场实施

5.1 谐波治理解决方案验证

增加RTDS自带的二阶带通滤波器(ωn=100π,ξ=0.1),电压前馈环节系统的波特图如图9所示。

图9 系统波特图对比Fig.9 Bode diagram comparison of the system

可以看到加入滤波后,系统在f=1/(2T1)附近频率和不加前馈环节基本一致,系统稳定性增强。

前馈电压环节加入滤波后,通过RTDS仿真试验验证前面所有试验中产生谐波谐振的现象均会消失。以Z4网络结构为例,加入前馈电压环节滤波后,即使在前馈电压环节再加入800 μs的延时,也不再出现高频谐波谐振的现象。

表1 有无前馈滤波环节的试验结果比对Table 1 Test results comparison with and without feedforward and filter loop

5.2 对其他功能的影响(解闭锁、低穿越、功率阶跃)

在前馈电压环节加入滤波后,在RTDS中测试了低电压穿越、解闭锁及功率阶跃等试验,发现前馈电压环节加入滤波前后对系统的动态特性几乎没有太大影响,甚至对相关性能起到了优化作用。以解闭锁为例,初步对比如下。

在Z1阻抗网络下,加入前置滤波前后,系统解锁时的相关波形对比见图10(a);加入前置滤波前后,有功功率阶跃响应的对比见图10(b)。

图10 系统解锁时的相关波形Fig.10 Relevant waveforms when system is unlocked

从图10(a)可以看到,加入前馈电压环节后,解锁冲击电流的峰值从1 700 A左右降低到了1 200 A左右,加入前馈电压环节后冲击电流更小些;从图10(b)可以看到,加入前馈电压环节后,功率阶跃响应基本一致。

5.3 现场实施效果

在前馈电压环节加入滤波后,在现场进行了实施。以低电压穿越为例,方案实施后低电压穿越成功,如图11所示。

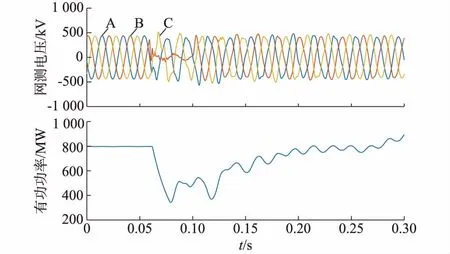
图11 低电压穿越波形Fig.11 Waveforms under low voltage ride-through

6 结语

通过对“4·10”广西侧谐波的特征进行分析,从鲁西背靠背柔性直流单元控制原理出发,推导了反映柔性直流对电网电压控制增益的传递函数,包括电压前馈环节控制传递函数、柔性直流谐波阻抗和交流系统谐波内阻抗等关键环节。通过对该传递函数的谐波稳定性分析,得出了前馈环节时延与系统阻抗在特定工况下,如换流站附近带有空充线路或者容性负载可能产生高频谐波谐振的规律,并经过了RTDS仿真验证。

同时本文还提出了在柔性直流电网电压前馈环节增加滤波环节进行高频谐波谐振抑制的措施,并通过RTDS仿真进行了验证,试验结果表明,完善后的柔性直流电网电压前馈控制逻辑可以有效抑制类似“4·10”的电网高频谐波谐振现象。该优化措施在鲁西背靠背工程的柔性直流单元得到了实施,为同类高频谐波谐振事件的处理提供了有益的参考。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。