基于储能实时修正双环控制的微电网能量管理方法

贾 科, 林瑶琦, 陈奕汝, 毕天姝, 刘搏晗

(1. 新能源电力系统国家重点实验室(华北电力大学), 北京市 102206; 2. 国网浙江省电力公司电力科学研究院， 浙江省杭州市 310014； 3. 国家电网交流建设公司, 北京市 100052)

0 引言

优化利用电网中各类能源发电是解决能源与环境问题的方法之一。然而微电网中可再生能源(renewable energy source,RES)出力(光伏、风电)具有间歇性和波动性,且与负荷需求呈不对等分布,给能源的本地高效利用带来挑战[1-3]。因此,利用储能系统协调能量供给和负荷需求的能量管理十分重要[4-12]。目前,能量管理方法主要分为启发式能量管理算法和模型预测控制(MPC)算法两大类。

启发式能量管理算法能在一定时间和空间范围内给出最优可行解。文献[13-15]以系统运行成本最小为目标函数,分别采用模糊控制、遗传算法实现系统能量流的优化控制。但上述算法都采用了日前控制的思路,需要根据RES预测出力预设储能系统运行模式,受预测误差影响较大。文献[16-18]采用启发式规则和粒子群优化(particle swarm optimization,PSO)算法相结合的方法优化储能充放电,提升算法实用性。但此类算法计算时间长且易陷入局部最优,不适用于运行复杂的系统。

MPC算法通过模型预测、滚动优化和反馈校正来解决有限时域开环问题。文献[19]提出一种基于模型预测控制的风储协调运行方法,可以解决风电间歇性出力功率波动问题,但未考虑储能对用户负荷削减的作用。文献[20-21]建立了考虑储能系统、电动汽车、可控分布式发电设备等的能量管理模型,有效降低了预测误差对系统运行成本和负荷削减的影响。但算法没有考虑对微型燃气轮机(简称微燃机)排烟的利用,未实现系统整体能源利用最优。

上述文献中提出的能量管理方法几乎都依赖于精确的RES和负荷预测数据,受预测误差的影响较大,难以应对电网中快速增长的随机、冲击负荷(如电动汽车等)。此外,在大多数能量管理方法中,储能元件是作为一种辅助元件,运行在满足其物理特性的约束条件下,而没有考虑其负荷削减作用。对此,本文提出一种基于预测数据实时修正的储能充放电算法,可以减小预测误差对算法控制带来的影响;同时,在调节用户负荷需求时,采用冷热电联产(combined cooling， heating and power,CCHP)方式和储能系统充放电控制相结合的方法,协同控制微燃机出力和储能的充放电功率,利用优化算法,构成双环协同控制,实现微电网能量的经济最优管理。该方法综合了启发式算法简单易行的特点和MPC修正误差的优点,负荷削减效果较好,可以减小持续增长的电动汽车等冲击负荷对于电网的影响。

1 微电网能量管理优化模型

本文研究微电网模型包括光伏、风机、微燃机、储能系统和负荷。光伏和风机运行于最大功率跟踪控制(不参与系统优化协调)。储能系统主要存储风、光的剩余能量用于削减高峰负荷。微燃机与储能系统协同参与能量管控。本文所提双环控制的外环是协调CCHP方式和储能系统,使供电成本最小,其内环在于利用储能实时修正实现最大负荷削减。

算法以系统可控供电成本最小为最终目标函数。因此,目标函数由微燃机供电成本CMT和主网供电成本Cb构成[22],如下式所示:

C=min(CMT+Cb)

(1)

式中:C为单位测量间隔内系统可控供电成本;主网供电成本Cb中包含低电价时主网向储能系统的充电成本。

储能成本越低,本文所提基于预测数据实时修正的算法对比于其他能量管理算法的优势越明显。考虑到随着新能源大规模并网,特别是部分地区明确要求储能配备,这势必将促进储能技术飞速发展及储能成本降低。基于对未来储能成本将进一步降低的判定,本文暂且不将储能成本纳入目标函数中。

1.1 微燃机供电成本

微燃机供电成本CMT由燃料成本Cf和发电成本Ce两部分组成[23],即

CMT=Cf+Ce=(pfVfuel+pePMT)Δt

(2)

(3)

式中:pf为燃气价格;Vfuel为单位时间内耗气量;Qfuel为燃料热值(与微燃机出力有关,见附录A表A1);λLHV为低位燃料热值(15 ℃,41.9 MJ/m3);pe为微燃机运行价格;PMT为微燃机出力;Δt为采样间隔时长(本文选为10 min)。

微燃机制冷功率PMT.cold和制热功率PMT.heat与微燃机出力PMT呈正相关关系。微燃机排烟通过热交换机可提供热功率。供热功率与微燃机出力关系如式(4)所示[24],系数θ计算方法如式(5)所示。

PMT.heat=θPMT

(4)

(5)

式中:ηhr为热耗率,其值为常数,依据微燃机型号而定;ηte为能源热效率;ηex为热交换机效率。

微燃机排烟通过溴化锂吸收式制冷机可提供冷功率。微燃机运行时,会产生一定温度和流速的排烟,数据如附录A表A1所示。根据制冷机的制冷特性,一定温度和流速的排烟通过制冷机产生冷功率,数据如附录A表A2所示。由于表A1和表A2中都是离散数据,因此本文采用拉格朗日二次插值方法计算微燃机的连续制冷功率PMT.cold。

由于用户用于调节室温的冷/热负荷需求具有明显的季节性,故微燃机不同时提供制冷和制热功率。冰箱、茶壶等一些对冷/热负荷需求较少的家用设备将通过电能直接供给。

1.2 运行约束条件

微电网中能量管理约束条件分储能系统充放电约束和微电网负荷需求平衡约束两方面。储能系统约束条件涉及储能容量、充放电功率和荷电状态(SOC);微电网负荷需求平衡涉及储能系统、光伏、风电、微燃机、主网与冷、热、电负荷平衡。

1)储能系统储能容量、充放电功率和SOC范围约束

储能系统储能容量Est不超过其极限值,如式(6)所示。

Est∈[Est.min,Est.max]

(6)

式中:Est.max为储能系统容量上限值,一般取储能系统的额定容量;Est.min为储能系统容量下限值,由最大放电深度决定[25]。

储能系统充放电功率Pst不超过其额定值,且受双向DC-DC变换器额定功率约束[26],如式(7)所示。

(7)

式中:Pst和Pst.e分别为储能系统充放电功率和额定功率;Pdde为双向DC-DC变换器额定功率;ηdd为双向DC-DC变换器效率。

为了防止过度充放电对储能系统造成损害,储能系统SOC必须限制在其最大、最小荷电量之间,如式(8)所示。

S∈[Smin,Smax]

(8)

式中:Smax和Smin分别为储能系统SOC的上、下限值。

储能系统的储能状态以能量E为描述单位,充放电控制过程则以功率P为描述单位。为描述E与P之间的数值关系,引入一个中间变量E′:

(9)

2)微电网负荷需求平衡约束

微电网中,储能系统、光伏、风电、微燃机根据用户负荷需求协调运行。其中冷(热)负荷需求主要由微燃机制冷(热)提供[27]。若用户冷(热)负荷需求得不到满足,则由光伏、风电、向主网购电通过空调制冷(热)的方式来补偿。负荷需求平衡约束条件如式(10)所示。

(10)

式中:Pc为用户剩余负荷需求功率;Ppv和Pwind分别为光伏和风电出力;Pb为主网供电功率;Pcold,Pheat,Pe分别为剩余冷、热、电负荷需求,由光伏、风电出力、主网供电和储能系统承担;PD.e,PD.cold,PD.heat分别为用户的电、冷、热负荷需求;α和β分别为制冷、制热系数(COP),为空调消耗单位功率所能获得的制冷、制热功率。

2 储能系统的充放电控制策略

储能系统充放电控制策略在目标函数寻优中起着综合协调能源系统削峰效果和经济性的作用。本文提出的基于预测数据的实时修正方法具体分为两步:①在每天初始根据当天预测负荷需求、RES预测出力计算储能系统当天的预充放电功率;②在实时运行中以储能系统的预充放电功率为参考值,根据实际负荷需求、RES实测出力计算实际充放电功率。该方法可以减小数据预测误差对负荷削减效果的影响。由于社区微电网中用户冷、热负荷需求具有明显的季节性且微燃机提供冷、热功率原理相似,因此,本文以夏季用户冷负荷需求最大的情形为例，具体阐述储能系统控制策略。

2.1 储能系统预充放电功率计算

当微燃机提供的制冷功率可以满足用户冷负荷需求时,储能系统只用于调节电负荷需求;反之,储能系统需要综合调节剩余冷负荷需求(将冷负荷需求值转换为由空调制冷提供等值冷负荷所需的电功率值)和电负荷需求。

首先,计算预测剩余功率Psp,判断储能系统运行模式。Psp为用户电负荷预测值、剩余冷负荷需求预测值之和与RES(光伏和风电)预测出力值之差,如式(11)所示。

Psp(i)=PD.e(i)+Pcold(i)-(Ppv(i)+Pwind(i))

(11)

式中:i为采样点。

其次,根据Psp值和阶梯电价划分,将储能系统运行模式分为以下三种情况。

1)当Psp为负(充电)时,若同时处于低电价时段,主网向储能强制充电。该充电功率受限于电池的额定功率、容量和电池SOC上限。

2)当Psp为正(放电)且处于低电价时,主网向储能系统强制充电。该充电功率满足第1种情况中限制。

3)当Psp为正且处于高电价时,储能系统处于放电模式。

其中,第3种情况需进行预放电功率的计算。在每天初始点先计算出当天储能系统中可用于调峰的预总功率Pava,作为计算预放电功率的约束值。该值为当天预测剩余功率负值部分(微电网系统供能大于负荷需求部分)和储能系统初始时刻自身可释放的功率之和,如式(12)所示。在计算实际充放电功率时,根据实际负荷需求情况控制微燃机的实际出力,将其纳入储能系统实际可释放功率中,以实现微燃机的经济运行。

[Est(144(d-1)+1)-SminEst.e]×3 600

(12)

式中:d为天数;Psp.neg为Psp负值部分;Smin是为了保证储能系统能长期稳定运行而设定的最小极限值;Est.e为储能系统额定储能容量；144(d-1)+1为每天初始点序列号(本文采样点采用连续编号方式,采样间隔为10 min,因此每天共有144个采样点)。

(13)

(14)

2.2 储能系统实际充放电功率计算

在储能系统实际充放电过程中,引入参数ΔP,用于表征储能系统能多用于负荷调节的功率。由于在计算预充放电功率时,未纳入微燃机出力对负荷削减的作用,故在计算完每天的预充放电后,若是储能系统SOC不会达到最小极限值,仍有剩余可用储能。因此,利用已得预充放电后储能系统当天高电价期间SOC最小值Smin′,计算这一部分剩余可用的功率ΔP,如式(15)所示。

ΔP(144(d-1)+1)=(Smin′-Smin)Est.e×3 600

(15)

此时,需由储能系统调节的实际剩余功率Psp′为用户电负荷实际值、剩余冷负荷需求实际值之和与光伏、风电、微燃机实际出力值之差,如式(16)所示。

Psp′(i)=PD.e′(i)+Pcold′(i)-(PMT′(i)+

Ppv′(i)+Pwind′(i))

(16)

式中:PD.e′为实际电负荷需求;Pcold′为剩余冷负荷需求实际值;PMT′,Ppv′,Pwind′分别为微燃机、光伏、风电实际出力。

储能系统实际充放电计算过程与预充放电功率计算过程类似,前两种情况一样。第3种情况下计算有所区别:将根据实测数据实时修正Pst,计算得到实际放电功率Pst′,也是本文所提算法的重要步骤。

第3种情况为当Psp′为正且处于高电价时,储能系统处于放电模式。在该情况下,若Psp′大于Psp,可增加储能系统的Pst′;相反,则可减少Pst′。储能系统增加或减少Pst′的计算方法具体分为以下两步。

1)若Psp为负则储能系统Pst′为:

(17)

2)若Psp为正则Pst′为:

(18)

在每一次计算完储能系统的实际充放电功率后,都需要重新校正ΔP的值。

1)若Psp为负:由于在计算储能系统预充放电功率时,Pava没有包含微燃机的出力,只包含了Psp负值部分,而在实际情况中,微燃机出力也能作为一部分储能补给。故校正ΔP如式(19)所示。

ΔP(i)=ΔP(i-1)-(Pst′(i)-Psp(i))

(19)

2)若Psp为正:ΔP的校正量为储能系统实际充放电功率与预充放电功率之差,如式(20)所示。

ΔP(i)=ΔP(i-1)-(Pst′(i)-Pst(i))

(20)

2.3 双环控制的微电网能量管理方法

在2.1节和2.2节对储能系统预充放电功率和实际充放电功率计算介绍基础上,通过图1展示基于储能实时修正双环控制的微电网能量管理方法的总体构思(图中A为连接符号)。

首先采用PSO算法[28]计算总体目标函数,寻找微燃机的最优出力值以综合协调微燃机出力、储能系统充放电和主网供给功率,这构成外环控制。PSO寻优算法的输入是微燃机出力的限值,输出是微燃机的最优出力值和目标函数的最优值。

图1 基于预测数据的实时修正算法流程Fig.1 Flow chart of real-time modification algorithm based on predicted data

该算法会随机产生一组粒子,一组中每一个粒子代表微燃机的一个可行出力值。粒子将跟踪两个极值:一个是粒子本身迄今为止找到的最优解;另一个是整个群体迄今为止找到的最优解,粒子的优劣将由目标函数决定。一组中每一个粒子相继进入PSO算法中嵌入的储能控制算法,得到相应的储能充放电功率和主网需承担的负荷,并计算目标函数值。将该组中每一个粒子得到的目标函数值进行比较,得到粒子本身最优解。之后,对粒子按一定速度进行数值增减得到一组新的粒子,重复上述步骤,得到相应的粒子本身最优解,并与上一组粒子本身最优解进行比较,得到群体最优解。如此重复,直至满足设定的最优精确度(相邻优化解之间的差值),即得到了微燃机的最优出力值和储能系统的最优充放电控制。

其次,针对储能系统充放电控制,称之为内环控制,共分两步:①在每天的初始点利用预测数据计算储能系统当天的预充放电功率(具体在2.1节中阐述);②根据实时数据修正预充放电功率以得到实际充放电功率(具体在2.2节中阐述)。

3 实验验证与对比

本文使用了英国诺丁汉大学“新能源住房系统”中4台3 kW风机和4台3 kW光伏系统的实测数据。电负荷数据和冷负荷数据皆由拉夫堡大学设计的CREST负荷用电模型生成[29]。阶梯电价曲线参考浙江电网峰谷电价标准,数据如附录A表A3所示。所选微燃机额定功率为30 kW,其运行成本相关数据(选取平均值)如附录A表A4[23]所示。储能元件选用5个20 kW·h/5 kW的Li-ion电池。由于Li-ion电池SOC在0.2～0.8之间时内阻较小且稳定,可以获得良好的功率特性[4,30],有利于电池长时间的工作,故设定电池工作SOC的上下限值(Smax和Smin)为0.8和0.2。用4 kW电动汽车(额定容量20 kW·h)模拟冲击负荷[31-33],并将冲击负荷随机加入特定时间内。

图2所示为光伏和风电3 d(72 h)的典型功率曲线。图中蓝色虚线为光伏出力,在每天正午左右达到峰值;绿色实线为风电出力,在每天清晨和深夜达到峰值。图3所示为用户电负荷和冷负荷需求(将冷负荷需求根据制冷能效比转换成所需电功率的数值,下同),在傍晚至深夜间达到峰值。图4所示为模拟电动汽车充电的冲击负荷曲线,与电负荷需求峰期时间一致。

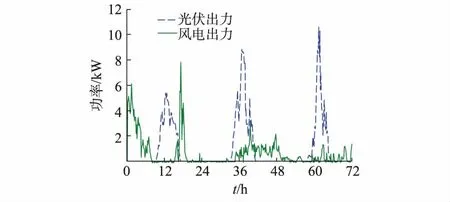
图2 光伏和风电输出曲线Fig.2 Photovoltaic and wind power output curves

图3 用户电负荷和冷负荷需求曲线Fig.3 Demand curves of consumer electrical load and cooling load

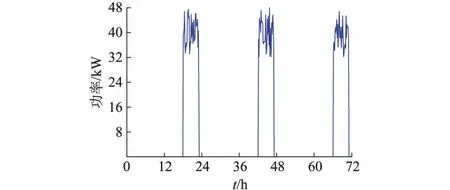
图4 电动汽车充电曲线(冲击负荷曲线)Fig.4 Charging curve of electric vehicle (impact load curve)

比较图2至图4可得,RES输出功率和用户负荷需求特性大致呈逆向分布。因此,利用储能装置对RES和负荷进行管理与调节,能最大限度地实现能源的本地利用和削减冲击负荷的目标。

为了凸显所提算法在削减负荷峰值方面的优越性,本文将该算法与固定阈值算法和自适应算法的运行结果进行比较分析。固定阈值算法[34]利用RES和负荷预测数据计算电池固定放电阈值Pthr(等于预测剩余功率总和的平均值)。在实际运行中,当实际剩余功率大于放电阈值且处于高电价时,电池放电调节负荷。自适应算法(AIT)[35]是一种根据电池前一天充放电情况(Pthr和充放电功率等参数)、电池当前SOC来实时调整电池当前时刻放电阈值和放电功率的方法。将这两种方法的运行结果与本文提出的基于预测数据实时修正方法的结果进行比较,如图5、图6所示。为了使结果对比明显,截取了其中一日的数据曲线图进行放大分析。

图5 经调节后的用户电负荷需求曲线Fig.5 Demand curves of electrical load after being dispatched

图6 供电成本曲线Fig.6 Power supply cost curves

图5所示为经调节后的用户负荷需求曲线。深蓝色虚线、绿色实线、红色实线分别为经固定阈值法、AIT和本文所提算法调节后新的负荷需求(包括电负荷和冷负荷需求)。从图中可知,三种方法都在不同程度上削减了负荷需求。其中,AIT和固定阈值法对电池的能量分配较为均匀,降低了对负荷峰值(43～47 h内)的调节效果。尤其对固定阈值法来说,其对预测数据精确性的依赖性大,调节冲击负荷能力有限。

本文所提算法相较于以上两种方法,虽然并未较好地削减需求较小时段内的负荷,但在削减负荷峰值(有冲击负荷出现的情况)时效果十分明显,缓解了电动汽车充电对电网的冲击影响,防止断路器因瞬时过负荷跳闸,保证电网和电池运行稳定性。

图6为三种算法的系统供电成本曲线。可知,在负荷需求较低的时段内,固定阈值法和AIT比本文所提算法供电成本低,而在负荷高峰期(电动汽车充电期间),本文所提算法比其他两种算法供电成本低(尤其是在43～45 h内)。这就更加证实了本文所提算法在应对冲击负荷时经济性更好,也从侧面体现出用户将会得到更多利益。

夏季7至9月是一年中电负荷和冷负荷需求高峰期,利用这段时间的负荷数据,分别采用上述三种算法进行长时间运行(共运行90 d)。为了比较出本文算法在应对冲击负荷时的经济性优势和冲击负荷削减优势,表1总结了电动汽车充电期间的结果。由该表可知,本文所提算法在电动汽车充电期间的负荷削减率达到74.24%,供电成本为19 654.7元,而其他两种方法的负荷削减率相对较低且供电成本较高。可见,本文算法在应对冲击负荷时不仅有经济上的优势,还有负荷削减效果上的优势。

表1 电动汽车充电时段电负荷削减结果比较Table 1 Results comparison of load shaving during electric vehicle charging period

将图5、图6和表1结合分析可得,AIT在平均分配电池储能上有较大的优势,但无法起到尽量削减冲击负荷的效果。相比于AIT算法和固定阈值算法,本文所提算法在处理冲击负荷情况中,不仅能较大程度地削减负荷,也体现出较好的经济性。当大规模电动汽车接入电网时,尽可能削减冲击负荷的优势对系统的健康稳定运行具有重要的意义。

4 结语

本文提出了一种基于预测数据实时修正的储能控制算法,考虑了电动汽车的充电负荷及CCHP的负荷调节作用。该算法首先利用预测数据计算出电池预充放电功率作为参考值,再根据实测数据,实时修正电池实际充放电功率。该算法不仅可以快速响应负荷变化(如电动汽车充电时产生冲击负荷的情况),而且具有一定的经济优势。通过实测数据验证分析显示,与固定阈值法和AIT相比,本文提出的储能控制方法不受储能系统放电阈值的影响,应用更灵活。此外,在应对冲击负荷时也有比较明显的削峰效果和经济优势。本文微电网中只考虑了光伏、风机、微燃机的供能及CCHP的运行方式,未来还可以进一步增加能源利用方式,考虑生物质能、氢能等新型能源的利用和储热等运行方式,建立综合能源模型,促进环境和经济的协调发展。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。