电力系统半线性与全线性最优潮流模型
卫志农, 朱梓荣, 赵静波, 刘建坤, 孙国强, 臧海祥
(1. 河海大学能源与电气学院, 江苏省南京市 211100; 2. 国网江苏省电力公司电力科学研究院, 江苏省南京市 211103)
0 引言
最优潮流(optimal power flow,OPF)计算于20世纪60年代由法国学者Carpentier[1]首次提出,是保证电力系统安全经济运行的重要手段[2-3]。然而,交流最优潮流(alternating current optimal power flow,ACOPF)模型具有很强的非线性特征,且其变量间的耦合十分紧密,这导致该模型的计算效率较低,无法满足大规模系统的在线实时计算需求。因此,寻找合适的线性化OPF模型显得尤为重要[4-8]。直流最优潮流(direct current optimal power flow,DCOPF)是目前求解速度最快的线性化OPF模型。但由于该模型忽略了网损,且不考虑电压幅值和无功功率的影响,导致其计算误差较大,无法获得完整的调度信息,存在一定的应用瓶颈[9-11],因此研究更精确的线性化模型具有重要的现实意义。
近年来,国内外众多学者对OPF的线性化模型展开了大量研究。文献[12]在DCOPF模型基础上,通过追加无功功率的方式对系统有功平衡方程进行修正,有效提高了DCOPF的精度,但该模型依旧未考虑网损因素的影响。文献[13]将线路损耗以变量的形式引入有功平衡方程中,并利用损耗特性对其增加约束,从而有效改善了系统的潮流分布。文献[14]在直流模型线路两端引入等效对地电阻,将线路有功损耗等效为两端电阻的损耗,从而有效模拟了线路损耗因素对系统的影响,但该模型仍然没有考虑无功功率和电压幅值的影响。文献[15]和文献[16]对不同阻抗比下的功率平衡方程进行拟合,分别提出一种计及电压幅值和无功功率的线性化潮流模型,有效提高了潮流计算的精度,丰富了可展示信息。但两种模型都在一定程度上弱化了线路两端的电压幅值差异,因此在进行OPF计算时,无功调度信息的误差较大。文献[17]利用泰勒级数展开的方法对系统功率平衡方程进行线性化处理,同时考虑了无功功率和电压幅值对系统的影响,但该模型基于热启动环境,操作点的选取会直接影响模型的计算精度。
基于此,本文首先对功率平衡方程中的三角函数项进行多项式拟合,再利用系统的运行特性将电压幅值和相角解耦,然后对其进行不同程度的泰勒级数展开,最终得到一种解耦的半线性化模型和一种全线性化模型。针对半线性化模型,本文从交流模型线路有功损耗公式出发,对现有网损等值负荷求解方式进行改良,提出一种基于改进网损等值负荷的DCOPF模型以为其提供良好的操作环境。而对于全线性化模型,本文将操作点代入循环中迭代更新,从而消除该模型对操作环境的依赖性。文章采用收敛性较好的原—对偶内点法(primal-dual interior point method,PDIPM)对各模型进行求解,结果表明,本文所提的几种模型能兼顾高效性和精确性,具有较高的应用价值。
1 半线性化OPF模型
本节提出一种电压相角线性但幅值非线性的OPF模型,由于模型中残留部分非线性项,因此线性化并不完全。为方便叙述,本文将此模型定义为半线性化模型,后续小节将对此模型进行详细推导。
1.1 ACOPF模型
ACOPF是一个典型的非线性规划问题,其标准形式包括目标函数、等式约束和不等式约束三个部分。本文选用常用的发电费用作为OPF的目标函数:
(1)
式中:ng为发电机个数;a2i,a1i,a0i为第i台发电机耗费特性参数;PGi为第i台发电机有功出力。
等式约束主要包括各节点的功率平衡方程:
(2)
式中:k∈i表示发电机k与节点i相连;PDi和QDi分别为节点i的有功负荷和无功负荷;Ui为节点i的电压幅值;θij=θi-θj为节点i和节点j的电压相角差;Gij和Bij分别为导纳矩阵第i行第j列元素的实部和虚部;nb为系统的节点个数。
同时,不等式约束主要包括:
(3)
式中:QGi为第i台发电机的无功出力;PLi和QLi分别为第i条支路的有功和无功潮流;nL为系统的支路条数;下标-和上标-分别为各变量的下限和上限。
1.2 电压幅值相角解耦及线性化处理
从ACOPF的标准模型可以看出,其非线性特征主要体现在节点功率平衡约束和线路潮流约束中,因此对线路潮流进行线性化处理是提高模型求解效率的关键。设i,j为线路L两端节点的编号,则线路潮流可写为:
(4)
式中:Pij和Qij分别为节点i流向节点j的有功功率和无功功率;gij和bij分别为线路的电导和电纳。
由于式(4)中存在大量三角函数项,导致电压幅值和相角的耦合比较紧密,不利于模型的线性化处理,因此需对其进行等效替换。根据系统线路两端的相角差通常在-π/6到π/6之间[16]的特性,本文利用MATLAB拟合工具箱对其进行拟合,从而得到以下等效关系:
(5)
为方便后续表述,令C1=0.97,C2=0.49。
同时,由于UiUj≈1,因此可得以下近似:
(6)
将式(5)和式(6)代入式(4)中可得:
(7)
式(7)中电压幅值和相角已完全解耦,但仍包含各变量的二次项,二次项的存在一定程度上会影响模型的求解效率,因此减少或去除模型中的二次项是提高模型求解效率的关键。目前对于二次项的线性化处理常采用泰勒级数展开的方式,但这需要在某一理想的操作点上进行,因此采用这一方法需要为其提供良好的操作环境。DCOPF仅通过相角表示系统平衡方程,具有求解速度快的优点,只要提高其计算精度即可提供良好的相角操作点。因此本文将式(7)中的相角二次项进行线性化处理,以减轻其非线性程度。为此,将θij的二次项进行泰勒级数展开,取其一阶项,并忽略截断误差,可得以下近似:
(8)
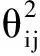
将式(8)代入式(7)中,可得:
(9)
此时,式(2)可变换为:
(10)
至此,电压相角线性但幅值非线性的半线性化模型就已表述完毕,而其所需的相角操作点信息将在第2节中进一步说明。
1.3 基于改进网损等值负荷的DCOPF模型
本文采用网损等值负荷直流模型为半线性化OPF模型提供相角操作点。该模型最早由文献[18]提出,文献[14]将其应用到OPF领域,附录A给出该模型的简述,其具体推导过程可参见文献[14]和文献[18]。上述文献均利用线路的有功功率和视在功率的关系近似描述线路损耗,该方法在等效过程中涉及线路视在功率幅值与有功功率幅值比例因子的计算。由于该参数在迭代过程中是一个不断变化的量,而上述文献将其设为定值,一定程度上会影响网损等值负荷模型的计算精度。基于此,本文从交流模型出发,重新推导线路有功损耗的计算公式,以求提高该模型的计算精度,从而为半线性化OPF模型提供更为良好的相角操作环境。由式(4)可得,交流模型中线路i-j的有功损耗Ploss,ij可表述为:
(11)
将式(5)代入式(11)中可得:
(12)
式中:Uij=Ui-Uj为线路两端的电压幅值差。
由于电力系统在运行过程中节点电压一般都保持在1.0(标幺值)左右,因此线路首末端电压幅值差的数值较小。而经过大量的算例验证,也可得Uij≪θij,因此可忽略式(12)中的Uij项,此时,式(12)可写为:
(13)
因此,基于改进网损等值负荷的DCOPF模型的约束条件可表述为:
(14)
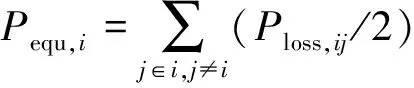
2 全线性化OPF模型
虽然1.2节将系统功率平衡方程中的电压幅值和相角解耦,并对其中相角二次项进行了线性化处理,在一定程度上提高了模型的求解效率。但将其应用在小系统OPF问题时对计算效率的提升并不明显,因此本节将对其中残留的幅值二次项进一步线性化处理,从而得到一种约束条件完全线性的OPF模型,为方便叙述,本文定义该模型为全线性化模型。
2.1 类热启动方式下的线性表达式
热启动方式[19]是指将电力系统日内调度的前一断面历史数据或者现行断面的潮流等类型的数据作为非线性项的泰勒级数展开的操作点。热启动方式下OPF模型的求解过程始终围绕所选取的操作点进行,因此,操作点的质量将直接影响计算结果的精度。由于目前缺乏快速而有效的提供幅值操作点的方法,本文借鉴热启动方式的思想,将每一次迭代所得结果作为下一次迭代所需的操作点,本文将这种处理方式定义为类热启动方式。此时,只需任意选择第一次迭代的操作点,随着迭代的进行,操作点不断更新,操作环境的质量也不断得到优化。采用这一方式,可有效消除模型对于操作环境的依赖性,从而避免操作点选择不得当而引起的计算误差和收敛性变差等问题。
基于上述类热启动方式,第k次迭代时有以下近似关系:
(15)
式中:θij,k-1,Ui,k-1,Uj,k-1分别为各变量第k-1次迭代所得结果。
将式(15)代入式(7)中,可得:
(16)
此时,式(2)可变换为:
(17)
2.2 操作点更新机制
因为线性化处理破坏了系统变量之间的固有关系,所以不存在最优操作点的概念,如果在整个求解过程中一直不停地更新操作点,反而会使算法的收敛性变差,增加模型求解所需承受的时间代价。因此,寻找合适的时机停止更新操作点有利于进一步提高模型的求解效率。为此,本文对所选用算法作相应的适应性分析。
本文采用PDIPM对模型进行求解,该算法的收敛判据是其对偶间隙Gap小于某一设定阈值,因此Gap能有效反映出当前结果与最优值之间的差距。而Gap可由式(18)求得[20]。
Gap=lTz-uTw
(18)
式中:l,u和z,w分别为PDIPM求解过程中引入的松弛变量和拉格朗日乘子。
以Polish 2736节点系统为例,附录B给出PDIPM在求解该系统ACOPF问题时Gap的变化过程(无可争议地,PDIPM在求解其他类似优化问题时,也具有相似的收敛特性)。从中可以看出,仅通过前几次迭代,该算法就将Gap快速收缩,此后Gap的变化趋势逐渐趋于平缓。这说明PDIPM在前几次迭代中就将目标函数快速收敛到最优值附近,而在后续求解过程中,每次迭代对目标函数的影响逐渐减小。此时,迭代对操作环境的改善作用也逐渐变弱,如果继续更新操作点,只会增加算法的计算成本。因此,当Gap的变化趋势趋于平缓时,停止更新操作点,既有利于获得良好的操作环境,也不会给算法造成过大的时间负担。
为了量化“平缓”的定义,本文根据PDIPM的收敛特性,定义当连续两次迭代所得的Gap之间的变化量小于第1次迭代时Gap的1%时,Gap的变化趋于“平缓”。由直线y=0.01x的斜率和PDIPM前几次迭代Gap的变化趋势易知,上述定义下Gap的变化趋势已足够平缓。同时,附录C给出PDIPM在求解OPF问题过程中,当Gap满足上述“平缓”条件时,目标函数与最优值之间的误差,进一步验证了本文对于“平缓”定义的有效性。此时,该模型的求解流程图如附录D所示。
至此,基于类热启动环境的全线性化模型及其操作点更新机制就已表述完毕。
3 算例分析
本文采用PDIPM对各模型进行求解,在MATLAB 2014a平台上实现算法编程。为验证各模型的有效性,本文对IEEE 300节点系统、Polish 2383节点系统、Polish 2736节点系统和一个8304节点大系统进行算例测试。为了方便表述,本文将ACOPF模型定义为AC,DCOPF模型定义为DC,文献[14]提出的基于网损等值负荷的直流模型定义为M1,本文1.3节所述基于改进网损等值负荷的直流模型定义为M2,文献[17]提出的基于热启动环境下的线性化OPF模型定义为M3,本文1.2节所述半线性化OPF模型定义为M4,本文2.1节所述全线性化OPF模型定义为M5。
为了保证测试环境的统一性,本文在求解各模型时,均采用相同的稀疏技术和收敛精度,以避免算法上的差异导致测试结果的不准确。
3.1 改进网损等值负荷直流模型校验
为验证M2为M4提供相角操作点的能力,本文先对其计算精度进行验证。表1给出AC,DC,M1和M2的计算结果,其中相对误差指的是该模型与AC模型之间的相对误差。由表1可知,M1和M2可有效提高DC模型的计算精度。同时,由于M2更精确地表述了线路损耗的近似公式,该模型成功将计算误差控制在了0.5%以内。

表1 直流类模型计算精度对比Table 1 Calculation accuracy comparison of DC-type models
而相对于目标函数,调度人员更关心OPF计算结果中的调度信息。同时,由于上述模型通过相角表述系统的平衡方程,调度信息的准确性间接反映出相角操作点的质量。因此表2给出上述模型的发电机有功出力情况,其中误差是指各模型与AC模型结果之间的误差。从中可以看出,M2有效改善了系统的潮流分布,提高了调度信息的准确度,既可以为M4提供良好的相角操作点,同时又具备成为独立的OPF模型投入实际应用的条件。
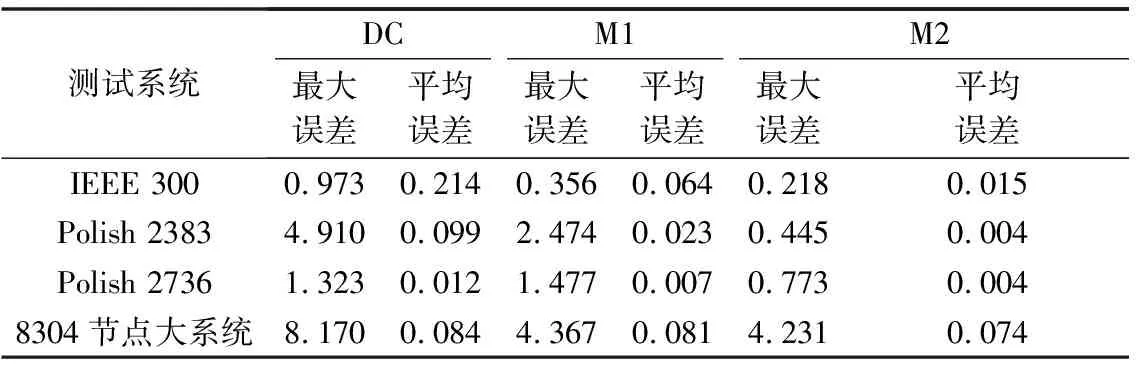
表2 直流类模型调度信息(发电机有功出力)对比Table 2 Scheduling information (generator active power) comparison of DC-type models
3.2 热启动类模型校验
M3,M4和M5均属于热启动类OPF模型,这一类模型对操作点的要求较高,操作点的质量会直接影响计算结果的精度。为验证各模型的精度和其对操作点的依赖性,本文分别选用系统的当前潮流和常用的平启动值(即电压幅值设为1.0(标幺值),电压相角设为0°)作为操作点对M3和M5进行校验,M4采用M2所得结果作为操作点。为方便叙述,本文定义潮流操作环境下的M3和M5分别为M31和M51,平启动操作环境下的M3和M5分别为M32和M52。
表3给出上述模型的计算结果,其中相对误差是指该模型与AC模型之间的相对误差。从中可以看出,对于绝大多数系统,M31均保有较高的精度,但M32的计算误差均超过1.5%,对于Polish 2383节点系统,其计算误差甚至达到了4.9%,这说明M3的计算精度与操作点的质量密切相关。而对于8304节点大系统,无论是以当前潮流还是平启动值作为操作点都无法为M3提供足够良好的操作环境,从而导致M31和M32在求解该系统OPF问题时无法有效收敛,这进一步说明了M3对操作环境的质量具有很强的依赖性,因此该模型的实际应用具有一定的局限性。

表3 热启动类模型计算精度对比Table 3 Calculation accuracy comparison of hot-start models
M4保留了功率平衡方程中的电压幅值二次项,因此较好地拟合了系统功率平衡方程与电压幅值之间的关系,而得益于M2为其提供的良好操作环境,该模型在求解各系统OPF问题时,均将计算误差控制在了0.5%以内。对于对操作点要求较高的8304节点大系统,该模型仍能有效收敛,且保有较高精度。因此结合本文所提模型M2,模型M4满足实际工程应用对计算精度的要求,具有较高的实用价值。
M5通过对操作点迭代更新的方式对操作环境进行了优化,因此无论是M51还是M52,在求解各模型的OPF问题时,也都将计算误差控制在了0.5%以内。同样对于对操作环境依赖性较高的8304节点大系统,M5也能有效收敛,且计算精度高,满足实际工程应用要求。从结果可以看出,M51和M52的结果基本一致,这说明2.2节对于“平缓”的定义是合理且正确的,该处理方式有效消除了M5对操作点的依赖性,扩大了模型的应用范围,使其具有较高的实用价值。
虽然目标函数可在一定程度上反映模型的精确程度,但无法有效表征系统无功调度信息的准确度。由M2可知,有功调度信息与电压相角的关联性较大,因此仅通过相角即可有效表述。不同于有功调度信息,无功调度信息需要由电压幅值和相角同时决定,所以发电机的无功出力可间接反映出系统状态变量的准确度。因此表4给出各模型解出的无功出力与AC模型所得结果之间的误差(本文采用的基准功率为100 MVA),为了更直观且清晰地展示各模型间的差异,附录E给出发电机数较少的IEEE 300节点系统的无功出力情况。可以看出,M4和M5较M3具有更高的精度,而由于M4保留了电压幅值的二次项,其无功调度信息较M5更为准确,与AC模型所得结果基本一致。虽然M4和M5所得结果中有极个别发电机的无功出力与交流最优解间的误差较大,但这并不会破坏系统的交流特性,附录F对这一结论进行了详细的分析验证。同时,M4和M5较好地解决了热启动类模型对操作点依赖性高的问题,且对8304节点大系统仍保有较高精度,因此,较M3具有更广泛的应用范围。

表4 热启动类模型调度信息(发电机无功出力)对比Table 4 Scheduling information (generator reactive power) comparison of hot-start models
3.3 各模型的计算效率对比
除了计算精度,计算效率也是评估线性化模型质量的重要指标之一。因此图1给出各模型在求解不同系统时所需的计算时间和迭代次数。
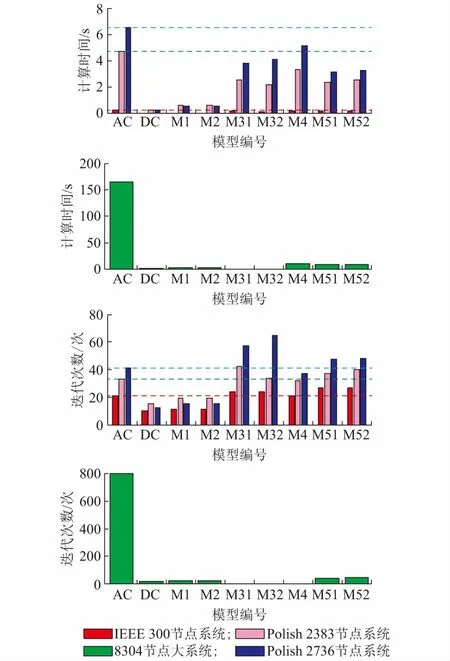
图1 不同模型所需计算时间和迭代次数对比Fig.1 Comparison of calculation time and iterations for different models
需要说明的是,图1中M4的计算时间未考虑操作点获取所需时间,因此其总耗时需要加上M2的计算时间。由图1可以看出,得益于MATLAB强大的计算能力和稀疏技术的应用,AC模型在求解大多数系统的OPF问题时,均能在50次迭代、7 s内有效收敛。但对于本文测试的8304节点大系统,AC模型需迭代796次,收敛用时约为165 s,远远超出了在线应用对于计算效率的要求,因此本文对线性化OPF模型的探究具有重要的现实意义。
在几种线性化模型中,由于DC模型对系统功率平衡方程做了大量简化,因此其迭代次数最少,计算效率最高,且对节点数较少的小系统该模型对效率的提升也十分明显。M1和M2的迭代次数和计算时间基本一致,由于这两个模型中都残留有非线性部分,因此其迭代次数和计算时间都略多于DC模型。但即便如此,其对OPF计算效率的提升仍然十分显著,即使是8304节点大系统,仍将计算时间控制在了2 s以内,相对AC模型减少了99%。
M3和M5在处理小系统OPF问题时,两者的计算效率基本相同。但对于大系统,例如Polish 2736节点系统,由于操作点的质量较差,M3的计算效率要略低于M5。而对于8304节点大系统,M3无法收敛,M5则仍能在50次迭代以内有效收敛,其计算时间较AC模型缩短了95%。
由于M4中残留有电压幅值二次项,因此在求解小系统OPF问题时,其对计算效率的提升并不明显,加之需要M2为其提供操作环境,该模型在求解IEEE 300和Polish 2383及Polish 2736节点系统的OPF问题时,相较AC模型只能缩短15%左右的时间。但对于8304节点大系统,M4对幅值和相角解耦处理的效果得以有效体现,将计算时间缩短到了12 s,相较AC模型减少了93%。
3.4 各模型的综合评述
3.1节至3.3节对各模型的计算精度和计算效率进行了详细的对比,基于上述结果,本节对各模型作简要评述。AC模型保留了系统全部特性,在求解小系统OPF问题时速度较快,因此当系统节点数在300以内时,可直接采用AC模型进行求解。DC模型虽然求解速度快,但其计算结果误差较大,调度信息不准确,因此无法投入实际应用。M2有效改善了网损等值负荷模型的计算精度,且并未因此影响其求解速度,故较M1具有更高的实际应用价值。M3通过泰勒级数展开的方式对三角函数进行线性化处理,因此其拟合程度较本文更高,但也正因为如此,其对操作点的依赖性很强,从而导致结果不够理想,若能快速为其提供更为良好的操作环境,该模型将具有很高的实用价值。M4和M5都对模型进行了解耦处理,有效提升了求解速度,且两者的计算精度都较高,具有较高的实用价值。但由于M4中仍残留非线性部分,因此在处理小系统OPF问题时,M4在提高求解效率方面略显乏力。相对的,由于M5对模型进行了全线性化处理,因此其计算精度较M4更低,因此,在实际应用过程中,对于两者的选用需对计算效率和精度作一定权衡。
4 结论
针对ACOPF计算效率低的问题,本文提出3种线性化OPF模型,通过对IEEE 300节点系统、Polish 2383节点系统、Polish 2736节点系统和一个8304节点大系统的算例测试,可以得到以下结论。
1)本文改进了网损等值负荷模型中等值网损的求解方式,从而有效提高了模型的计算精度,使其即可为本文所提半线性化模型提供良好的操作环境,也可成为独立的线性化OPF模型投入实际应用。
2)本文所提解耦的半线性化模型和全线性化模型包含完整的调度信息,计算精度高,求解效率较快,有效解决了热启动类模型对操作环境依赖性高的问题,具有较高的实用价值。但对于两者的选用需在求解效率和计算精度之间作一定权衡。
未来可进一步研究线性化模型在N-1校验、机组组合、预防/校正控制等方面的应用,以进一步体现线性化模型的优势。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

