基于Sobol’法的孤岛微电网潮流全局灵敏度分析
何 琨, 严 正, 徐潇源, 王 晗
(电力传输与功率变换控制教育部重点实验室(上海交通大学), 上海市 200240)
0 引言
微电网是一种集分布式电源(distributed generator,DG)、分布式储能(distributed storage,DS)、负荷、变流器和继电保护装置等于一体的小型低压发配电系统[1]。交流微电网有并网运行和孤岛运行两种模式[2]。对于并网运行的微电网,当所接入的大电网故障时,可进入计划外孤岛运行,提高了微电网的供电可靠性;同时,微电网也可主动脱离大电网孤岛运行,有利于获取更好的效益。近年来,风电、光伏发电[3-4]等可再生能源接入微电网的比例逐步提高,并且考虑到微电网中的负荷随机性强[5],源荷不确定性对孤岛微电网运行状态及潮流分布的影响愈加显著,评估输入变量对微电网状态的影响,辨识影响系统状态的关键因素,对提高微电网运行控制水平具有重要价值。
概率潮流(probabilistic power flow,PPF)[6]是一种有效的电力系统不确定性分析方法,其能全面考虑随机因素的影响,获得节点电压和线路潮流的概率分布和统计数字。孤岛微电网与传统输电网相比具有显著差异,采用传统牛顿—拉夫逊(Newton-Raphson,NR)法计算潮流时可能会出现雅可比矩阵奇异的情况[7]。目前,针对孤岛微电网潮流计算,文献[8]将下垂控制节点等效为PQ节点,并采用Gauss-Seidel法求解,但收敛速度慢;文献[9]考虑微电网的下垂特性,利用牛顿信赖域法,通过计算二阶海森阵求解微电网潮流模型,计算量大。由于微电网的源荷不确定性会使其运行状态复杂多变,潮流分布与预设运行状态偏差较大,因此需采用鲁棒性和收敛性更强的孤岛微电网概率潮流计算方法。
针对微电网潮流的不确定性,灵敏度分析能定量分析输入随机变量对系统输出的影响,辨别影响系统状态的关键因素。灵敏度分析包括局部灵敏度分析(local sensitivity analysis,LSA)和全局灵敏度分析(global sensitivity analysis,GSA)。LSA用于分析参数变化对系统输出的局部影响,在电力系统中已得到广泛应用。文献[10]通过逐次线性化思路,建立了潮流无功优化的灵敏度模型,并采用对偶线性化求解以简化计算;文献[11]以梯度为基础,提出一种基于直接求导法的断面潮流定向控制方法,且满足不同潮流目标变动的定向要求。LSA的主要缺点是要求输入变量变化范围较小,且一般适用于线性模型。GSA基于输入随机变量的概率分布,适用于非线性、非单调的复杂系统,分析输入变量的单独作用及交互作用对系统输出的影响。目前GSA在电力系统中应用较少,文献[12]采用多元回归法,引入粗糙集理论与D-S证据理论,对负荷预测的经济、社会、气候等因素进行灵敏度分析;文献[13]基于傅里叶幅度灵敏度检测法,分析了影响系统频率和阻尼的关键因素。但这些方法只定性分析了输入对系统输出的影响程度。Sobol’法[14]是数学家Sobol提出的一种基于方差的GSA方法,其将系统输出方差分解为由各输入变量所决定的方差之和,从而定量分析输入变量对系统输出的影响。
本文计及微电网的源荷不确定性,基于有功—频率/无功—电压(P-f/Q-U)的下垂控制策略,构建了综合控制下的孤岛微电网概率潮流计算模型,并采用自适应LM(Levenberg-Marquardt)算法求解潮流方程。进一步,提出了基于Sobol’法的孤岛微电网潮流GSA方法,用于评估输入随机变量对潮流分布的影响。通过对33节点孤岛微电网进行算例仿真,分析了可再生能源的不确定性对微电网潮流的影响,准确辨识影响系统状态的关键输入变量,验证了所提方法的有效性。
1 孤岛微电网的概率潮流模型
传统的电力系统潮流计算中,通常将节点分为PQ,PV和平衡节点;而综合控制下的孤岛交流微电网不含平衡节点,由下垂控制的DG调节系统的频率和电压。本文考虑微电网中DG和负荷的不确定性,建立综合控制下的孤岛微电网概率潮流模型。
1.1 孤岛交流微电网潮流模型
1)孤岛微电网模型
孤岛交流微电网中,DG装置可处理为PQ节点、PV节点和下垂控制节点3种类型[15]。考虑滤波器、变压器等感性元件及虚拟阻抗方法的应用,逆变器型DG接入时,线路等效阻抗呈感性[16]。因此,本文下垂控制节点采用P-f/Q-U的控制策略,其下垂特性曲线如附录A图A1所示。由此可得孤岛微电网中下垂控制节点i的功率方程为:
(1)
式中:PGi和QGi分别为节点i流入系统的有功和无功功率;npi和nqi分别为节点i的有功、无功下垂增益;f0和U0i分别为节点i的空载频率和空载输出电压幅值;f为系统的运行频率;Ui为节点i的节点电压幅值。
根据孤岛交流微电网系统的频率和电压允许的调节范围,DG节点i的下垂增益满足:
(2)
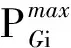
综合控制下的孤岛交流微电网中,系统频率一般不稳定在工频,需考虑负荷节点电压和频率对负荷模型的影响[17],其负荷节点有功和无功功率与节点电压、频率之间的关系可参考文献[18]。孤岛交流微电网安全稳定运行时,其频率偏差在系统允许的波动范围内对线路参数的影响很小[16],因此,本文假定线路参数不随系统运行情况而变化。
2)孤岛微电网潮流方程
综合PQ,PV及下垂控制节点的功率方程,建立孤岛交流微电网的潮流方程如下:
(3)
式中:U为节点电压幅值向量;θ为未知节点电压相角向量;PGi和QGi分别为节点i处DG或DS装置输出的有功和无功功率;PLi和QLi分别为节点i处实际的有功和无功负荷;Pi和Qi分别为节点i的注入有功和无功功率;SPQ,SPV,SD分别为微电网中PQ,PV及下垂控制节点集合。
可将式(3)表示为如下紧凑形式:
F(x)=0
(4)
式中:x=(f,U,θ)。
当PV节点或下垂控制节点的输出功率超过给定限额时,将转化为PQ节点,功率保持在限定值。
进一步,考虑到模型中的DG有功功率PGi和无功功率QGi、负荷有功功率PLi和无功功率QLi的不确定性,待求的解x也具有概率特征。因此,称式(4)为综合控制下的孤岛微电网概率潮流模型。
1.2 源荷不确定性
本文计及孤岛微电网中DG出力与负荷的不确定性,进一步研究源荷不确定性对系统潮流的影响。对于可再生能源发电,采用非参数估计建立其概率分布;对于负荷,采用正态分布描述其不确定性。
1)DG出力的不确定性
可再生能源发电受到天气、时节等环境因素的影响,其出力具有间歇性和波动性,常用的参数模型,例如威布尔分布和Beta分布[19],不一定能准确描述其实际的概率模型。核密度估计(KDE)[20]是一种非参数估计方法,根据输入变量的样本拟合其概率密度函数(PDF),能更为准确地描述随机变量的分布特性。
假设随机变量x的N个样本为{x1,x2,…,xN},则x概率密度函数的核密度估计为:
(5)
式中:h为带宽;K(·)为核函数,且满足式(6)所示条件。
(6)
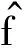
(7)
由式(5)和式(7)可知,核密度估计得到的随机变量的累积概率分布为:
(8)
式中:Φ(x,xi,h)为期望为xi、标准差为h的正态分布的累积分布函数(CDF)。
通过核密度估计得到风速和光照强度的概率密度函数和累积分布函数;然后采用基于拉丁超立方采样(LHS)的蒙特卡洛模拟(MCS)对风速和光照强度进行采样;最后根据文献[21]获得风电和光伏出力样本。
2)负荷的不确定性
本文中假定系统负荷的功率因数不变,负荷有功功率的波动呈正态分布:
(9)
通过设置不同的标准差σi构造不同程度的负荷波动,并利用基于LHS的MCS得到具有随机波动性的负荷样本。
2 自适应LM算法
相比于传统电网,孤岛微电网具有以下特性:①网架结构呈辐射状且常为开环运行;②系统线路分支众多且线径较细,导致线路R/X较大;③在对等控制或综合控制下[1],系统无平衡节点,由下垂控制的DG调节频率和电压[22]。针对孤岛微电网的潮流计算,本文采用具有较强收敛性和鲁棒性的自适应LM算法求解式(4)的潮流方程。在传统LM算法的基础上,引入自适应阻尼因子,保证在迭代过程中雅可比矩阵始终非奇异,且能根据当前迭代情况调整迭代方向和迭代步长,有效求解包括“病态”情况在内的潮流方程。自适应LM算法[23]具有收敛范围广、对初值不敏感、鲁棒性强等优点,即使在潮流方程无解的情况下也能给出最小二乘解,为后续系统调整提供参考。LM算法主要步骤如下。
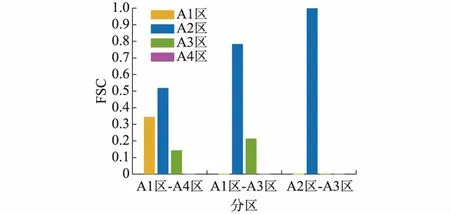
步骤1:设初始迭代次数g=1,收敛精度ε,最大迭代次数G,初始自适应因子α1,常量α1>m>0,0 步骤2:对潮流方程F(x)=0左侧在当前迭代点xg处一阶泰勒展开,即F(xg+1)=F(xg)+J(xg)dg,其中dg=xg+1-xg为迭代步长。 步骤3:通过优化问题求解迭代步长,可表示为: dg=-(J(xg)TJ(xg)+μgI)-1J(xg)TF(xg) (10) 式中:μg为阻尼因子;dg包括步长值和方向。 步骤4:自适应阻尼因子的选取原则为μg=αg‖F(xg)‖,其中αg>0为自适应因子,其调整方式取决于当前迭代步的有效性。 步骤5:引入评价指标rg来判别当前迭代的有效性,评估F(x)实际与预期下降量的比值,即 (11) 步骤6:如果rg>p0,则接受当前步长,更新迭代点xg+1=xg+dg,并按式(12)调整自适应因子。 (12) 步骤7:如果‖J(xg)TF(xg)‖<ε或达到最大迭代次数G,则迭代结束,输出当前迭代点,否则g=g+1,并返回步骤2。 Sobol’法是一种定量评估系统GSA的方法,基于方差研究单个输入变量或多个输入变量之间相互作用对系统输出的影响,其基本理论如下。 假设x=[x1,x2,…,xk]为定义在Ωk上的独立输入变量,不失一般性,Ωk可表示为: Ωk=(x|0≤xi≤1;i=1,2,…,k) (13) f(x)为平方可积函数,基于函数的高维模型(HDMR)表示,可将其分解为2k个子函数之和[24]: (14) 式中:fi=fi(xi),fij=fij(xi,xj),f12…k=f12…k(x1,x2,…,xk),其他高阶分解项可以此类推;f0为常数。 对于函数f(x),存在下述定理。 定理1:对于独立的输入变量,当基于式(14)的分解项fi…j满足式(15)时,式(14)的分解唯一,即 (15) 式中:1≤i1<… (16) 且所有分解项均可由函数f(x)的积分形式得到: (17) 式中:x~i表示除xi以外的输入变量集;x~(ij)表示除xi和xj以外的输入变量集。 对分解式(14)平方并积分可得: (18) 则函数f(x)的总方差为: (19) 偏方差为: (20) 因此可得: (21) 则定义输入变量的灵敏度如下: (22) 根据灵敏度系数的定义可将式(21)改写为: (23) 式中:一阶灵敏度系数(FSC)Si(1≤i≤k)表示输入变量xi对系统输出的主要影响,Si越大,表明xi的不确定性对系统输出的影响越大;二阶灵敏度系数Sij(1≤i 在实际应用中,描述系统传递关系的解析函数f(x)通常较为复杂,而系统的输入变量和输出结果相对易于得到。Sobol’法的一个显著优点是,当无法获得函数分解的解析式时,可采用MCS计算式(19)、式(20)的积分,这一思想拓展了基于Sobol’法的GSA在实际工程中的应用范围。 (24) 式中:xs为输入变量第s次采样值;x(~i)s为除xi以外的其他输入变量的第s次采样值;xis为输入变量xi的第s次采样值。 进一步可得出xi的FSC和TSC估计值为: (25) 本文建立了综合控制下孤岛微电网的概率潮流计算模型,并提出了基于Sobol’法的GSA方法,通过基于LHS的MCS,实现对系统频率、节点电压及系统潮流的全局灵敏度分析,辨识影响系统输出的重要输入变量,具体流程如图1所示。 图1 孤岛微电网概率潮流GSA流程Fig.1 Flow chart of GSA for probabilistic power flow in islanded microgrids 本文在IEEE 33节点的网架结构基础上接入4个DG和1个DS装置,构成的33节点孤岛交流微电网系统如附录B图B1所示。该系统包含4个分区,系统的基准电压为12.66 kV,基准容量为1 MVA,基准频率为50 Hz,各节点处所接负荷类型参见文献[26]。其中,4个DG包括2个风机、1个光伏和1个燃气轮机。风速和光照强度的原始数据为中国西部某地一年的统计数据;2个风机的额定容量分别为800 kW和1 000 kW,风机的切入风速、额定风速、切出风速分别为3,15,20 m/s;光伏阵列面积为4 000 m2,光电转换效率为14%;风机和光伏均采取就地无功补偿的方式,且保持功率因数恒定;假定本算例中DS处在放电状态,处理为PQ节点;燃气轮机作为下垂控制节点,用于调节系统的电压与频率。其参数设置:Umax和Umin分别为1.06和0.94(标幺值),fmax和fmin分别为1.004和0.996(标幺值),有功、无功功率的下垂增益分别为0.005 56和0.08(标幺值);系统的基准总负荷为3.55+j1.979(标幺值),负荷波动满足正态分布,期望为原始数据,标准差为期望的1%。 对于系统的某一稳定运行状态,当考虑微电网负荷波动时,结合MCS对具有随机波动的负荷进行20次采样,并分别采用NR法和自适应LM方法进行潮流计算,两种算法的潮流计算结果相同,其收敛速度如附录B图B2所示。 由于综合控制下孤岛微电网内不存在平衡节点,且系统线路的阻感较大,因此,进一步增大线路的阻感比,并设置不同的初值以测试算法的鲁棒性和收敛性。当线路阻感比为初始值的5倍且节点电压相角初值为0.08、电压幅值初值为1时,NR法出现大量不收敛情况,而自适应LM算法仍然收敛,两种算法的收敛特性如附录B图B3所示。通过对比可知,自适应LM算法对初值依赖度低,具有更强的收敛性,适用于孤岛微电网的概率潮流计算。 通过MCS得到样本容量为50 000的风电与光伏的输入样本,采用自适应LM算法进行潮流计算,分析各个输入变量针对不同输出结果的灵敏度。 1)系统频率 由于系统频率是判别孤岛微电网是否稳定运行的重要指标,因此有必要分析各输入变量针对系统频率的全局灵敏度。风机1、风机2,以及光伏对系统频率的FSC的收敛情况如图2所示,FSC和TSC的具体数值如表1所示。 图2 输入变量对系统频率的FSCFig.2 FSCs of input variables with respect to system frequency DGFSCTSC风机10.345 10.350 2风机20.515 30.515 9光伏0.139 30.140 2 由图2可知,孤岛微电网的系统频率受风机2出力不确定性的影响最大,其次为风机1,受光伏出力不确定性的影响最小。由表1可知针对系统频率,风机和光伏的FSC之和为0.999 7,十分接近1,同时,对于每一个可再生能源DG,其TSC略大于FSC,表明可再生能源发电的交互作用对系统频率影响很小,系统频率的概率分布主要由各输入变量单独作用决定。因为FSC与TSC相差很小,所以本文主要以FSC作为辨识系统关键因素的指标。 2)节点电压幅值 可再生能源出力针对下垂控制节点(节点38)电压幅值的FSC如附录B图B4左侧所示。下垂节点的电压幅值受各DG出力不确定性的影响由大到小分别为风机2、风机1、光伏。针对系统频率和下垂节点电压幅值,可再生能源出力的FSC排序相同。这是因为在本算例中风机和光伏的功率因数相同,因此下垂节点的有功、无功出力受到可再生能源DG出力影响程度的排序相同,因此对于系统频率与下垂节点电压幅值,3台DG的FSC排序一致。 进一步,针对节点12的电压幅值,3台可再生能源DG的FSC如附录B图B4右侧所示。对比DG出力对于下垂节点与节点12电压幅值的FSC可知,在孤岛微电网中,不同节点的电压受到各个DG出力随机性的影响不同。节点12接近风机1,相较于其他节点,其节点电压幅值的概率分布受风机1出力随机性的影响最大,其次为风机2,受光伏出力随机性的影响较小。 3)线路潮流 对于A3区中线路5-6的有功和无功功率,可再生能源DG的FSC如附录B图B5所示。由图可知,线路5-6的有功和无功功率的不确定性主要受风机2的影响,其次为光伏,受风机1出力不确定性的影响基本为0。并且针对同一条线路的有功和无功功率,各个DG的FSC基本相等。 3台可再生能源DG对于A1区中线路11-12传输的有功和无功功率的FSC如附录B图B6所示。可知风机1的FSC接近于1,而风机2和光伏的FSC接近于0。这是因为线路11-12接近风机1,其传输的有功和无功功率的波动基本只受风机1出力不确定性的影响。 进一步,设置如下3种情况,以验证基于Sobol’法的FSC用于辨识系统关键因素的有效性。case1:3台DG出力均为随机变量;case2:风机1出力为随机变量,风机2和光伏出力分别取其概率分布的均值;case3:风机1出力取其概率分布的均值,风机2和光伏出力为随机变量。针对以上3种情况,得到线路11-12传输有功功率的CDF如图3所示。可知,当仅考虑重要输入变量(case2)时,其结果与考虑所有随机输入变量(case1)的CDF基本一致;反之仅考虑不重要的随机输入变量(case3)时,其CDF与case1相差很大。因此,基于Sobol’法计算得到的FSC能有效地辨识出影响系统输出变量概率分布的重要输入随机变量,进而有利于减少电力系统随机问题的输入变量维度,提高计算效率。 图3 不同情况下有功功率的累积分布Fig.3 Cumulative distributions of active power for different scenarios 根据附录B图B1所示的微电网分区,考虑分区内DG出力的随机性及负荷的波动性,分析区域联络线上的潮流受分区源荷不确定性的综合影响。对于3条区域联络线传输的有功功率,各个分区内DG和负荷不确定性的FSC如图4所示。 图4 各分区随机变量对联络线潮流的FSCFig.4 FSCs of random variables with respect to power flow of tie-lines 由图4可知,不同区域联络线传输的有功功率受各分区内源荷不确定性的影响程度不同,A4区不存在可再生能源DG,负荷波动对各条联络线传输有功功率的概率分布基本没有影响。A2区内的源荷不确定性是影响各条联络线传输有功功率概率分布的关键因素;A1区内的源荷不确定性主要影响了A1区和A4区之间联络线上传输的有功功率。 本文针对综合控制下的孤岛交流微电网潮流,计及DG出力和负荷波动的不确定性,建立基于自适应LM法的孤岛微电网概率潮流计算方法,提出了评估输入随机变量影响的GSA方法,并应用于33节点孤岛微电网系统。主要结论如下。 1)针对孤岛微电网的潮流计算,与NR法相比,自适应LM方法在收敛范围和初值敏感性方面有一定的优势。 2)不同位置、不同类型、不同容量的DG对系统频率、节点电压、线路潮流的影响不相同,Sobol’全局灵敏度系数准确辨识了影响孤岛微电网状态的关键因素和非关键因素。 3)对于待研究的系统输出指标,如果某输入随机变量的灵敏度系数很小,则表明该变量的不确定性对结果的影响近似为零,可考虑将其取为固定值,从而降低系统变量维数,简化模型。 GSA能够辨识孤岛微电网运行中关键的不确定性因素,进而对系统关键DG节点增加储能装置或加强监控管理,有利于增强系统运行的稳定性。下一步工作会进一步考虑如何提高GSA方法的计算效率,并且进一步分析GSA的实际应用。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。3 基于Sobol’法的全局灵敏度分析
3.1 Sobol’法
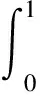
3.2 基于MCS的全局灵敏度系数计算
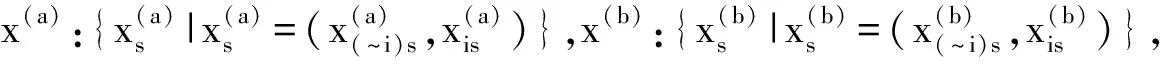
4 孤岛微电网潮流的全局灵敏度分析流程
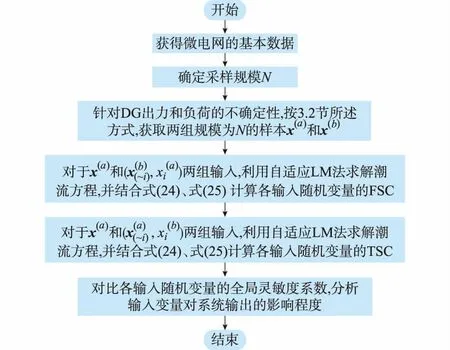
5 算例分析
5.1 算例数据
5.2 自适应LM算法
5.3 DG出力不确定性的全局灵敏度分析
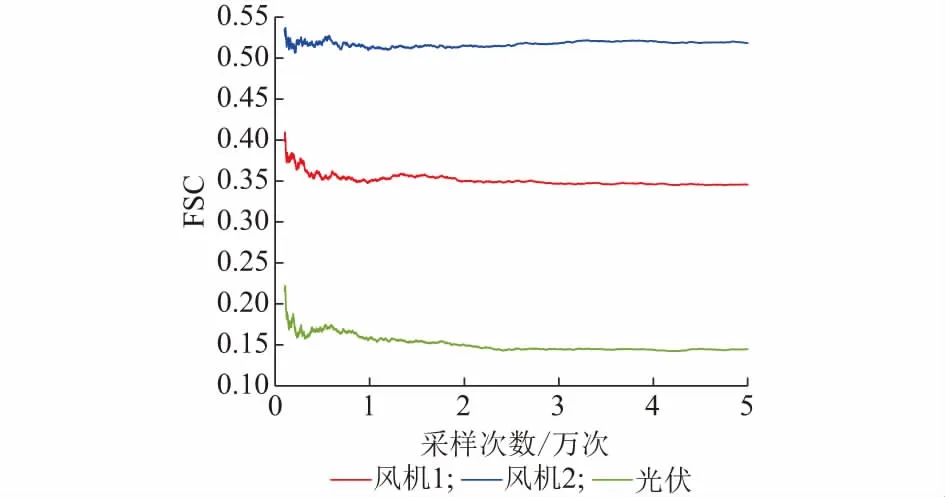
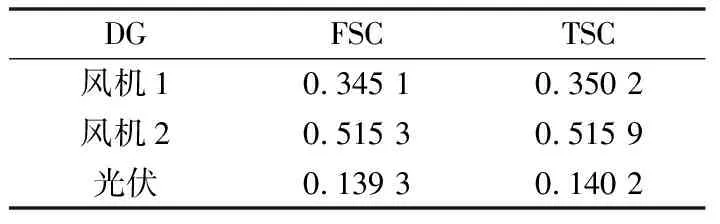
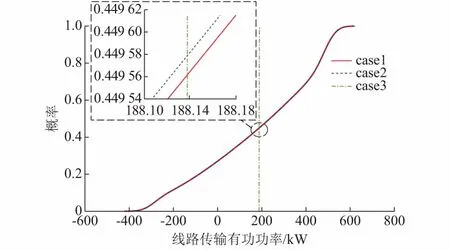
5.4 分区内源荷不确定性的全局灵敏度分析
6 结论

