抑郁症患者正性情绪加工脑电样本熵异常研究

朱嘉诚 李颖洁 曹 丹 唐莺莹

(1. 上海大学通信与信息工程学院生物医学工程研究所，上海 200444;2. 上海交通大学医学院附属精神卫生中心脑电影像室，上海 200072)

1 引言

抑郁症是由各种原因引起的、常见的情感障碍疾病，主要临床表现为与情绪相关的行为及认知等活动异常[1]。研究表明，抑郁症患者的情绪认知存在一定偏差[2-3]。传统的脑电线性分析研究发现，与正常人相比，抑郁症患者不同频段中脑电功率的激活都存在异常[4]。但是，脑电作为典型的非线性时间序列[5]，传统线性分析的稳定性和敏感性等均不尽如人意[6]。近二十年来，非线性分析方法逐步被应用到脑电分析中，例如“熵”就是测量复杂度的一个典型指标。Aftanas等应用非线性分析方法研究了受试者在不同情感刺激(正性、中性和负性)下的变化情况, 认为非线性分析相比线性分析对情感处理的细微方面更敏感[7]。但目前基于熵的抑郁症脑电研究还存在一些问题，其中一个突出的问题是已有研究普遍关注的是全频段的特性[8]。然而，这些全频段的复杂度特性结果却不统一。例如，有研究发现相比于正常人，抑郁症患者的脑电复杂度下降[9]。另一些研究却得出了相反的结论，认为由于抑郁症患者负性情绪偏向导致脑电复杂度增加[10]。所以，需要更细致的研究。

为了解决或规避全频段脑电复杂性结果不统一的问题，我们尝试关注不同频段脑电的复杂度。通常我们通过基于傅里叶变换的方法来获取脑电某频段信号，但是传统的傅里叶变换要求系统必须是线性的，同时数据必须严格具有周期性或平稳性[11]。针对非线性系统，黄鄂等人在1998年提出了希尔伯特-黄变换[12]，一种自适应的时频分析方法[13]。他们通过一种经验模式分解(empirical mode decomposition， EMD)方法，将复杂的信号分解为一些线性和平稳的分量。研究表明，对于诸如脑电信号、心电信号这类非平稳，非线性的信号希尔伯特-黄变换有更好的应用效果[14-15]。提取的特征是否可以用于机器自动分类是检验特征鲁棒性的一个有效方法。大部分的脑电信号分类研究在脑电特征提取时会选用信号的常规统计特征，如能量和功率谱密度。然而研究表明，针对大脑不同的活动，各脑区的活跃程度也不同[16]。而从不活跃的脑区中提取的特征，会包含许多冗余信息，从而可能影响脑电信号特征的分类结果。

同时，熵的具体计算方法也有很多种，它们各有特点。例如，研究表明近似熵可以作为脑电信号的一个特征来区分不同的脑部活动状态[16]；K-S熵允许通过信息生成率来分类不同状态下的脑电活动[17]，但容易受到噪声影响，同时计算量大[18]；样本熵是由Richman等人在2000年提出的一种描述时间序列复杂度的度量参数[19]。相较于近似熵，样本熵具有更好的精确度和鲁棒性；同时样本熵对于丢失数据不敏感，计算速度快。

针对抑郁症患者在情绪加工中的脑电非线性特异性问题，本研究中我们采用希尔伯特-黄变换对原始脑电数据进行滤波获取各频段脑电，然后选取有特异性的脑电频段计算样本熵，进而分析比较抑郁症患者的情绪加工与正常人之间的差异。最后再根据这些具有明显差异的特征值分类正常人与抑郁症患者，检验分类效果。

2 材料和方法

2.1 受试者

本实验中，我们将受试者分成实验组和对照组。实验组中包括抑郁症患者16名，其中男性6名，女性10名，平均年龄为37.75±14.19岁，平均受教育年限为12.06±2.91年，均为右利手。抑郁症患者来自上海市精神卫生中心的门诊病人，均符合中国精神障碍分类与诊断标准(CCMD-3)，无狂躁史；对照组中包括健康受试者14名，其中男性4名，女性10名，平均年龄为40.86±12.29岁，平均受教育年限为11.54±3.75年，均为右利手，没有任何神经或精神病史。经过统计检验，两组人在年龄和受教育年限上无统计学差异(见表1)。所有患者均未服药或未服药至少一个月，包括对照组的所有受试者都无药物史和酗酒史，视力正常或者矫正视力正常。在实验前，所有受试者都经过了焦虑自评量表(self-rating anxiety scale，SAS)、抑郁自评量表(self-rating depression scale，SDS) 和汉密尔顿抑郁量表(Hamilton depression scale，HAMD) 的评定，对照组的评分在正常范围内，表明无精神疾病，如表1所示[20]。所有受试者在实验前均签署了知情同意书，实验结束后均给予受试者适当的报酬，实验经过了上海市精神卫生中心人类伦理委员会的批准。

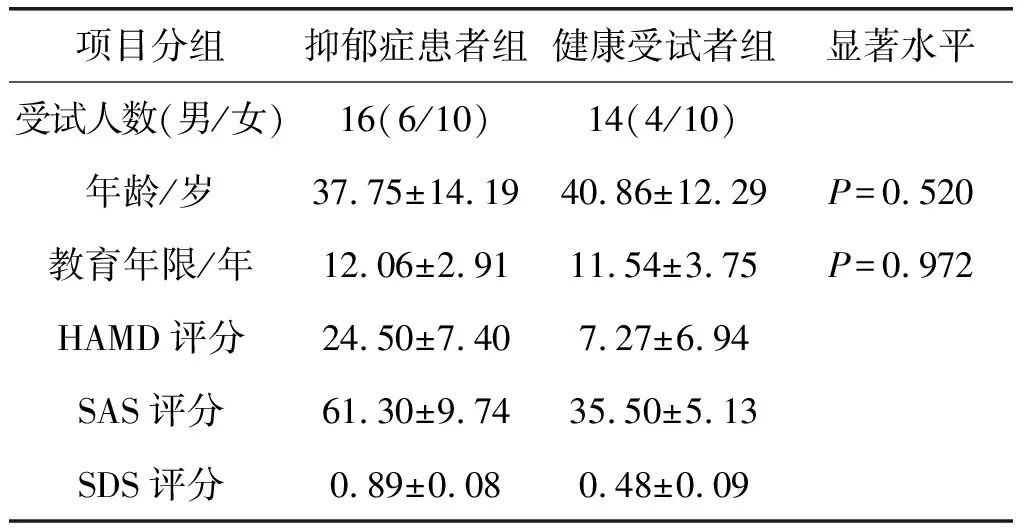
表1 受试者自评量表

2.2 实验范式

本实验是根据Williams等人的心理物理实验构建的[21]一个电生理的情绪面孔空间检测任务。刺激图片来源于Ekman情感数据库[22]，同一个人脸分别有三种情绪(积极的，消极的和中性的)，每张面孔均没有头发、眼镜、胡子，或其他面部配饰。所有图片都使用Adobe Photoshop软件编辑并转换为灰度图片。刺激图片中，同一个人的六张面孔，其中五张为中性表情，另一张为带有情绪的面孔(积极或消极)。这张情绪面孔随机地出现在六边形的六个顶点上。整个实验包含4组，每组包含144张刺激图片(即72个积极情绪，36个消极情绪，36个中性情绪)，每张刺激图片呈现时间为1500 μs，紧接着出现1000 μs的刺激间隔，此时电脑屏幕上呈现白色“+”号。然后，在屏幕中央单独出现固定十字时，呈现1000 ms的刺激间隔(ISI)。实验中的事件序列如图1所示。实验采用Go-Nogo范式，实验程序由美国PST(Psychology Software Tools)公司的E-Prime 1.0软件编写。

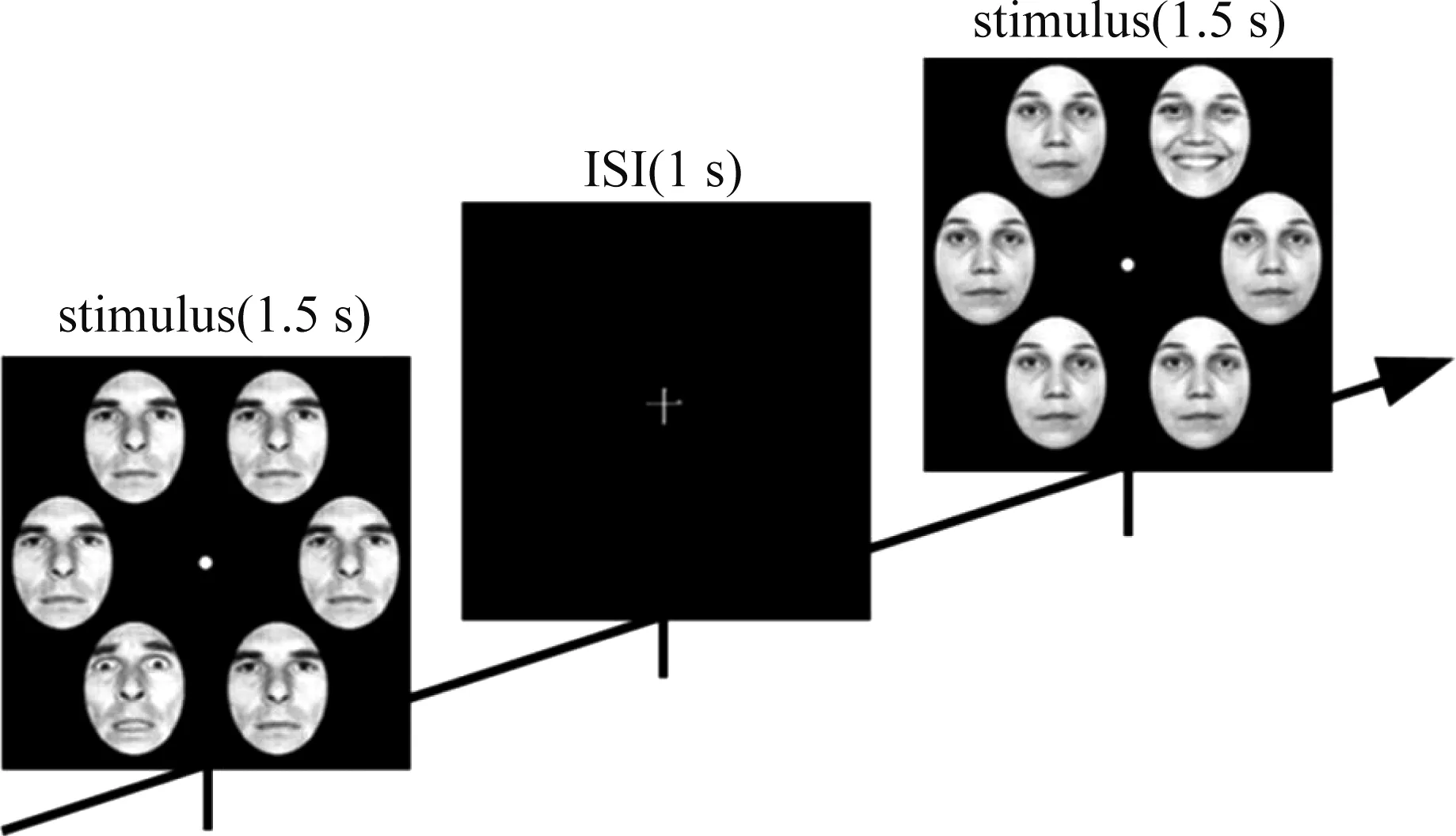
图1 实验范式Fig.1 Experimental paradigm

实验过程中，受试者舒适地坐在距离17英寸液晶显示屏80厘米处，指示他们看着屏幕中央的”十”号，所有受试者被要求尽快尽准确的判断是否有目标面孔出现并做按键反应。如果看到正性表情的面孔，要求他们按键“1”；如果看到负性表情的面孔，要求他们按键“5”。每组实验之间有1分钟的休息时间，整个实验需要大约30分钟。

2.3 数据采集与预处理

实验数据采集设备为德国Brain Productions(BP)公司的64 导高密度的脑电检测仪; 记录软件采用该公司研发的Vision Recorder系统; 数据预处理采用Vision Analyzer系统。本实验从覆盖整个头皮的64个电极中去除了损坏的电极，最终选择了59个电极，：Fp1，Fpz，Fp2，AF7，AF3，AF4，AF8，F7，F5，F3，F1，Fz，F2，F4，F6，F8，FT7，FC5，FC3，FC1，FC2，FC4，FC6，FT8，T7，C5，C3，C1，Cz，C2，C4，C6，T8，TP7，CP5，CP3，CP1，CPz，CP2，CP4，CP6，TP8，P7，P5，P3，P1，Pz，P2，P4，P6，P8，PO7，PO3，POz，PO4，PO8，O1，Oz和O2，具体位置如图2所示。数据记录以鼻尖为参照，脑电信号的采样频率为1000 Hz，电极与头皮间的接触阻抗保持在5 kΩ以下。

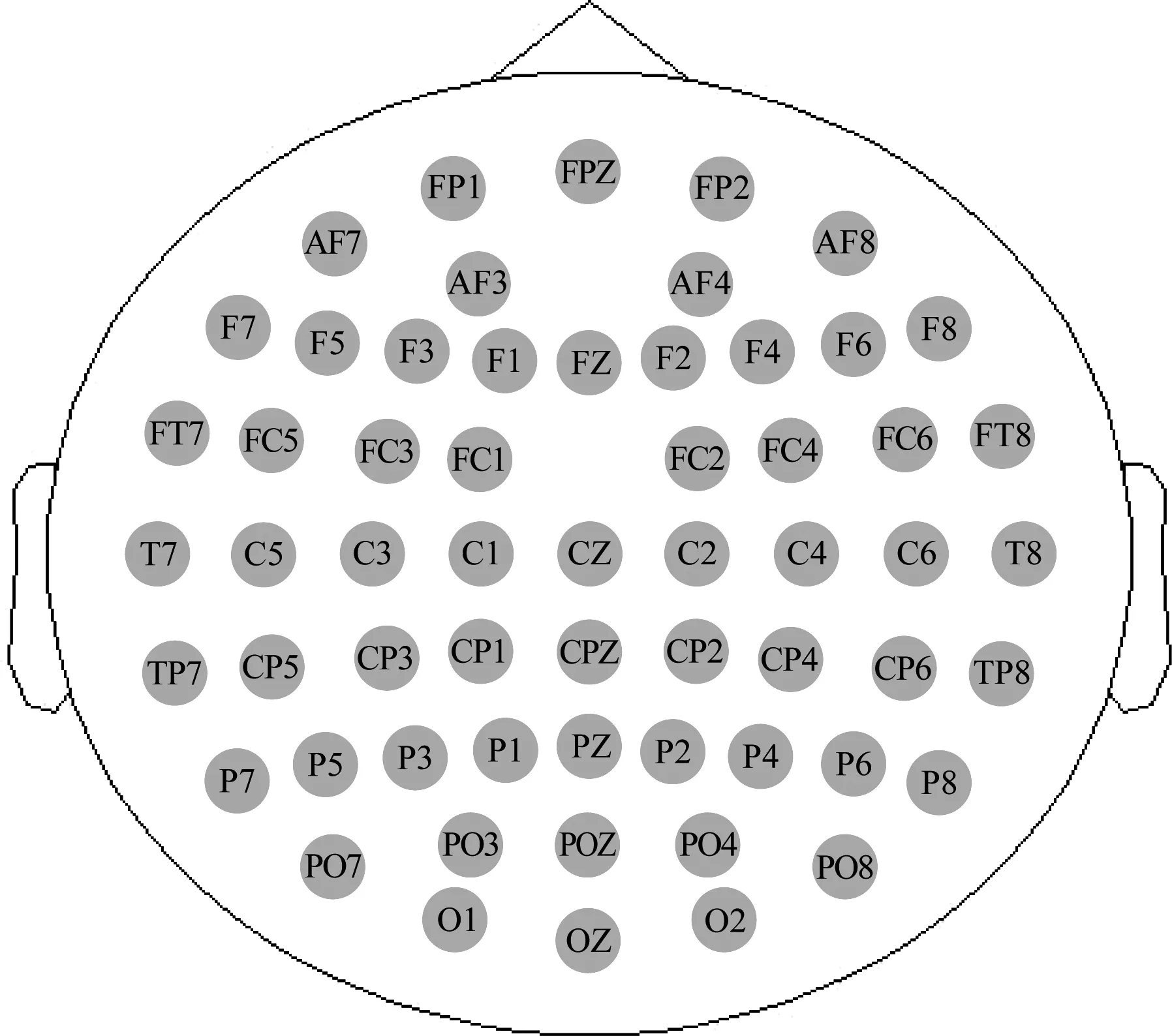
图2 脑电电极位置图Fig.2 Electrode location

经过下面的预处理，我们便获得了干净的脑电信号：(1)使用BP公司的Vision Analyzer系统的眼电校正算法，将眼电伪迹去除；(2)对去除伪迹的数据进行0.05和100 Hz的带通滤波；(3)将数据从刺激发生前200 μs到刺激后1000 μs进行分段，并且进行基线校正；(4)剔除伪迹大于100 μV 的数据段。最后将数据导出进入后续分析。

2.4 信号分析处理

2.4.1 希尔伯特-黄变换

希尔伯特-黄变换包含两个步骤：经验模态分解和希尔伯特变换(Hilbert transform，HT)。通过EMD将信号分解成有限个内在模分量(intrinsic mode functions，IMF)和一个残余信号，然后对得到的各个IMF分量进行希尔伯特变换。计算流程如图3所示。

图3 希尔伯特黄变换的流程图Fig.3 Hilbert-Huang transform flowchart

本文中，设xi(t),(i=1,2,3,…,59)代表单个电极上的脑电信号，首先找到xi(t)的极大值和极小值，通过拟合，得到其上包络Uix(t)和下包络Lix(t)，以及上下包络的均值mi1(t)。然后，从xi(t)中减去均值mi1(t),得到第一个分量hi1(t)。

要判断hi1(t)是否是一个真正的IMF分量，需要满足两个条件：(1)hi1(t)的极值点包括极大值和极小值，与过零点的数目相等，或不超过1个。(2)均值线的均值要趋于0。

如果不满足这两个条件，再次重复上述步骤直至其满足条件。最终得到的hi1k(t)可以被认为是第一个IMF分量C1。然后将xi(t)中减去C1，从而得到残余信号ri1(t)。重复计算，直至将最后的IMF分量分离出来。

因此，xi(t)可表示成以下公式(1)：

(1)

其中，rin(t)表示最终的残余信号，EMD分解的终止条件是当残余信号是一个单调函数，即找不到极值点时，分解完成。因此它是一个常数或者单调函数，表示了单通道脑电信号xi(t)的趋势变化。

通过EMD分解得到有限多个IMF分量后，第二步是对每一个IMF分量做希尔伯特变换，来找到信号的幅值-时间-频率分布，也称为希尔伯特谱。

首先，对每个IMF做希尔伯特变换，表示为公式(2)：

(2)

(3)

解析信号的实部为各个IMF信号，虚部为经过希尔伯特变换后的信号。其中，ak(t)表示IMF分量ck(t)的瞬时幅值，ϑk(t)表示IMF分量ck(t)的瞬时相位。

从而，可以得出各个IMF分量ck(t)的瞬时频率的公式(4)：

ωk(t)=dθk(t)/dt

(4)

根据上述希尔伯特-黄变换的理论，我们在实验中计算得出了各个IMF分量的瞬时频率后，将单通道脑电信号划分成了四个频段，分别是：δ(1～4 Hz)、θ(4～8 Hz)、α(8～13 Hz)、 β(13～30 Hz)，应用于后续的数据分析处理。

2.4.2 样本熵

样本熵是根据近似熵的算法进行改进得出的，本文用SampEn(m,r,N)来表示，其中N表示序列的长度，r表示相似容限，m表示维数。具体计算过程如下：

首先，将原始单通道脑电信号序列按特定顺序组成一组m维的矢量：

X(i)=[x(i),x(i+1),…,x(i+m-1)],

i=[1,N-m+1]

(5)

定义X(i)与X(j)之间的距离dij为两者对应元素中差值的最大值：

dij=max0-m-1|x(i+k)-x(j+k)|

(6)

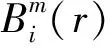
(7)

然后再对i做平均，记为Bm(r)

(8)

把维数m加一，变为m+1，重复上述公式(5)～(8)，得到Am(r)。

因此，最终的样本熵定义为：

(9)

从公式(9)可以发现，样本熵的值与参数m,r,N的选择有关，根据文献[23]，在本研究中我们选取的参数值为N=Xi(t),m=2,r=0.2SD，按照此参数值计算得到的样本熵具有较为合理的统计特性。

2.5 统计分析

本实验采用软件SPSS 22.0进行统计分析，运用重复测量方差分析方法。组内因素为面孔表情(正性/负性)，脑区域(额区/中央区/顶区/枕区)，脑半球(左/右); 组间因素为组别(抑郁症组/正常组)。若存在交互效应，则进行简单效应分析。统计结果P值若小于0.05，则认为存在显著性差异；如果P值在0.05到0.10之间，则认为存在差异性趋势。

2.6 分类器选择

本文针对小样本数据，选择支持向量机、K-近邻算法、决策树算法作为分类器，根据统计分析得出明显差异的样本熵特征送入分类器进行分类，比较各分类器对于本数据集的应用效果。

本数据集包括16名抑郁症患者和14名正常人，以2/3的样本作为训练集，1/3的样本作为测试集，最终19个样本作为训练集，11个样本作为测试集。

支持向量机(SVM)的核心思想是通过使用核函数将低维空间线性不可分的样本转化为高维特征空间使其线性可分，并在特征空间中构建出最优分割超平面。它在很大程度上解决了过拟合、非线性和维灾等问题。

K-近邻算法(KNN)通过计算不同特征值之间的距离作为各个样本之间的非相似指标，一般使用欧氏距离。它的分类思路是如果一个测试样本与特征空间中的K个最相似(即欧氏距离最近)的样本中的大多数属于某一类别，则该样本也属于这个类别。该算法需要已知训练集中数据和标签，并且不需要训练模型，具有计算量小的优点。

决策树算法一般由两个步骤来实现，首先通过训练集进行训练来生成一个决策树，进而建立决策树结构。然后通过使用生成的树来实现对输入的测试样本进行分类，对输入的测试样本，从根节点位置依次测试样本的属性，通过对比选择合适的树支，直到到达某个叶结点，从而得到该测试样本的类别。

3 结果与分析

3.1 抑郁症患者β脑电样本熵结果异常

已有研究表明，β频段与外部刺激和情绪认知反应显着相关[24]。具有高比例β频段的人思考快速，感到兴奋，并处于高认知功能状态[25]。在我们的研究中，尽管做了全频段的分析，但最终我们的发现集中在β频段上。具体地， 针对16名抑郁症患者和14名健康受试者在β频段的样本熵数据，分别进行均值和标准差的计算，并进行比较分析。结果显示，抑郁症患者呈现出显著低于正常人的脑电样本熵。样本熵的值反映了脑电信号的随机性[17]。样本熵越高，代表神经动力学的规律性越小，随机性越大[26]。研究表明，相比于情感障碍的患者，正常人的脑部活动具有不规则性[27]，和更高的复杂性[28]。重复测量方差分析显示，β活动呈现出显著的区域主效应(F=14.390，P=0.001)，以及区域与组的交互效应(F=4.533，P=0.024)。进一步固定区域做简单效应分析，对于健康对照组，不同情绪刺激影响下的脑电样本熵具有差异性趋势(顶区F=4.257,P=0.060，枕区F=3.898,P=0.070)，正性情绪刺激和负性刺激相比，诱发出更高的脑电样本熵。但对于抑郁症患者组的脑电样本熵没有显著差异，这也证实抑郁症患者对不同情绪的认知功能存在缺陷。表2给出了相关的简单效应分析结果。

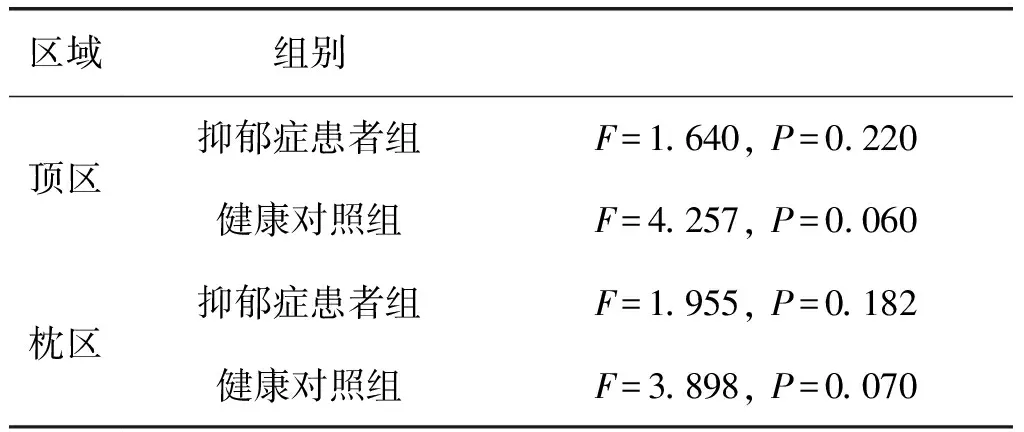
表2 不同脑区的脑电样本熵的组间差异

同时，分析发现，在正性面孔刺激下，显示出区域的主效应(F=17.483，P=0.001)，以及区域与组的交互效应(F=6.832，P=0.002)。分别对各脑区进行进一步分析，发现在大脑的中央区的脑电信号样本熵上具有显著组间差异(F=13.477,P=0.001)，与正常人相比，抑郁症患者在大脑的中央区的脑电样本熵更低。(参见表3)。可见抑郁症患者中后部脑区情绪加工确实存在异常[29-31]。

表3 正性情绪刺激下的组间差异

我们的研究结果表明抑郁症患者对于正性情绪的加工出现了异常。许多研究表明，抑郁症对负性情绪有认知偏向[19]，抑郁症患者更容易对负性情绪进行加工，对于负性情绪面孔的认知优于正性情绪面孔[32]。在我们的研究中表现在其脑电样本熵上明显低于正常人，证实了抑郁症患者认知正性情绪刺激的能力低于正常水平。

3.2 分类结果

通过希尔伯特黄变换，首先得到每个电极的样本熵，根据左额区(F3,F7)、右额区(F4，F8)、左中央区(C1,C3)、右中央区(C2,C4)、左顶区(P3,P7)、右顶区(P4,P8)、左枕区(O1)和右枕区(O2)，将同一区域的电极样本熵做平均，从而得到8个区域、4个频段、2种情绪任务共64个样本熵特征向量。经过重复测量方差分析得出抑郁组与正常组在β频段具有明显差异，于是选择β频段上各脑区的样本熵特征，一共16个。将全频段64个特征与β频段16个特征分别送入三种分类器中，识别准确率如表4所示。

本研究的结论表明，抑郁症患者与正常人脑电样本熵存在显著差异，可见脑电样本熵是一种潜在的可用作抑郁症患者分类的度量指标。根据表4的结果可见，通过本文统计分析后得到的具有明显差异的特征值对分类准确率的提升有很大的帮助。统计结果表明所筛选出的β频段各脑区样本熵特征在两类人群中具有明显差异，此结论极大地消除了脑电信号中大量的冗余信息，为分类识别提供了更准确的特征，同时降低了训练模型和分类的计算时间。本研究结果还显示对于小样本量的数据集，支持向量机算法相比K近邻、决策树算法具有更好的识别准确率，计算时间更短。能够在保证降低误诊率的同时，极大节省计算机辅助诊断的等待时间。

此外，我们还比较了基于小波变换提取的样本熵与基于希尔伯特黄变换提取的样本熵的分类效果。本文选取db5小波函数对整段脑电信号进行分频处理，根据各脑区的划分，得到16个样本熵特征。分类结果如表5所示。

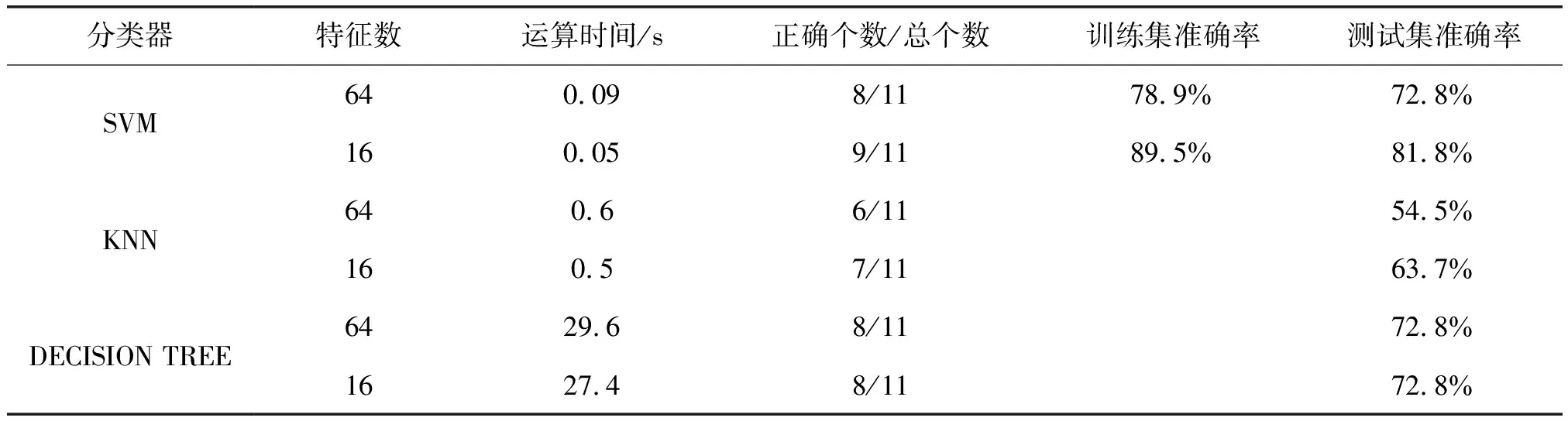
表4 基于不同特征数的分类结果

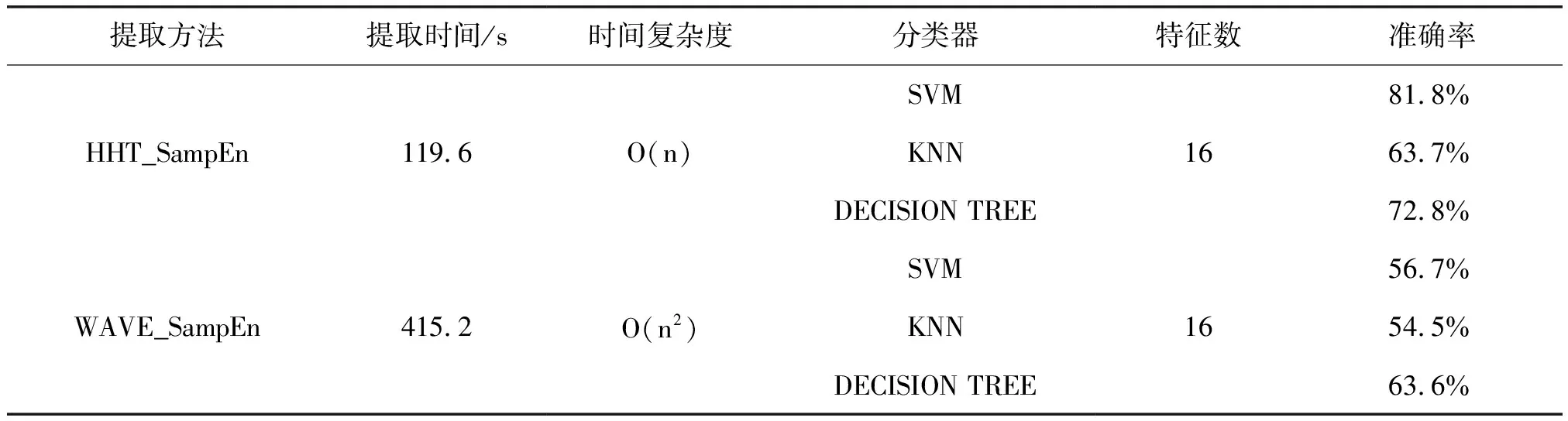
表5 基于不同分频方法的分类结果

从表5结果得出，基于希尔伯特黄变换的提取特征的方法时间复杂度远远小于基于小波变换的方法，在同等运行条件下的实际运算时间也更短。同时结合希尔伯特黄变换和样本熵的分类准确率也远高于小波变换结合样本熵的分类准确率。本研究结果一定程度证明了希尔伯特黄变换能够保留更丰富的脑电信号的非线性复杂度特征，刻画出脑电信号的局部信息。

4 结论

本研究结果显示抑郁症患者在做正性情绪刺激任务下，在大脑中央区上具有低于正常对照组的样本熵，提示抑郁症患者在正性情绪的加工上存在缺陷，为抑郁症的发病机制提供了电生理证据。此外，本文所应用的基于希尔伯特黄变换的样本熵特征，经过本实验验证，可以有效区分正常人与抑郁症患者，在深入研究的基础上，有望用于抑郁症患者的分类识别，为医生诊断抑郁症提供一种可行的辅助方案。