面向事件相关电位成分的稀疏字典构建方法

李海峰 丰 上 马 琳 徐睿峰 徐忠亮

(1. 哈尔滨工业大学计算机科学与技术学院，黑龙江哈尔滨 150001； 2. 哈尔滨工业大学(深圳)，广东深圳 518055； 3. 东北林业大学信息与计算机工程学院，黑龙江哈尔滨 150040)

1 引言

事件相关电位(Event-related potential, ERP)指的是在特定的感觉、认知或运动事件后，在头皮观测到的大脑电反应[1]。一般而言，ERP可以指任何对应某种刺激的固定的电生理反应。ERP提供了一种评估大脑功能的非侵入手段。ERP可以通过采集脑电图(electroencephalography，EEG)来获得。EEG包含了近千个同时进行的脑部活动的电信号，其中跟刺激或事件有关的大脑活动所占比例很小，因此为了能够清晰的获得大脑对刺激的响应，需要对原始EEG信号做处理之后才能获得ERP波形[2]。最常用的是叠加平均法，实验过程中同样的刺激重复多次，把每次采集到的EEG波形进行叠加平均，使得随机的大脑活动在信号中占比逐渐降低，最终获得ERP的波形。

叠加平均法的前提假设是与事件相关的电位波动在多次观测中会保持一致，而噪声也可以近似为零均值高斯随机过程[2]。叠加之后，噪声的能量逐渐降低，而ERP波形会保持一致。这样做的问题是，许多与认知状态有关的信号成分会在叠加过程中被消耗掉[3]。如果有一种能够单次刺激之后获得的EEG数据中提取ERP波形的方法，就可以避免有关的信号成分被损耗，同时通过分析ERP波形随着时间的变化，可以分析认知状态随着实验进行是否有波动[4]。

随着信号处理技术的进步，越来越多的研究开始将重点放在EEG信号或ERP波形的稀疏分解上[5- 6]。稀疏分解的方法非常适用于非稳态、包含成分有限的信号，例如语音信号和EEG信号[7]。利用稀疏分解方法，每段EEG数据可以算作一帧，利用已知字典就可以求解每帧数据的稀疏表示系数[8]。获得系数之后，既可以在便携设备上实现EEG数据的压缩传输[9]以及伪迹祛除[10]，也可以利用系数实现ERP波形的单次提取和识别[11]。

K-SVD字典学习算法[12]是目前最广泛应用的，能够给出相对严格意义的稀疏解的稀疏分解算法。K-SVD是一种字典学习算法，用于通过奇异值分解方法创建用于稀疏表示的过完备字典。 K-SVD是k-means聚类方法的一种推广，它通过在基于当前字典的稀疏编码输入数据之间迭代交替工作，并且更新字典中的原子以更好地适合输入数据。Zhang等[13]利用K-SVD算法获得的字典，实现了车辆驾驶员的警觉度检测；Nagaraj等[14]把患者的EEG信号使用K-SVD算法进行字典求解和稀疏建模，实现了癫痫发作的实时检测。

但是利用K-SVD进行EEG信号分解时，由于初始字典原子常用稳态信号，很难获得能够准确描述非稳态EEG信号的原子，EEG信号中的成分，尤其是ERP相关成分，极易混杂在大量字典原子中。为了解决上述问题，实现将EEG信号分解为具有实际意义的，可以用于EEG信号按事件分帧之后的单次ERP成分提取的稀疏分析方法，本文提出了将稀疏性能评价指标用于稀疏字典构建过程中作为迭代训练过程中的约束条件，结合成熟的K-SVD算法，最终训练出包含完整ERP波形的稀疏字典。

本文在第2节介绍基于稀疏性能约束的稀疏字典训练方法，在第3节介绍基于这个方法对一个公开EEG数据集的ERP波形进行稀疏分析的操作步骤，在第4节展示了利用这一方法获得的结果。结果表明，本方法可以有效的将ERP成分提取到稀疏字典原子中。

2 基于稀疏性能约束的稀疏字典训练方法

2.1 稀疏性能指标

信号的稀疏建模是通过将字典D=[d1|d2|…|dM]∈RN×M中的原子dk进行线性组合,对信号y∈RN进行表示的过程，如式(1)所示。

y=DA+e

(1)

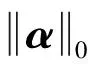
(2)

(3)

字典学习的过程是对一个训练集Y={yi|i=1,2,…,p}，训练字典D，并通过该字典求解问题P0或P(0,ε)，得到每一个yi对应的稀疏模型Ai=(Ai1,Ai2,…,Ain),令线性表示yi=DAi+ei中的误差ei最小。为了求解这一问题，用l1范数代替l0范数作为约束条件的稀疏字典求解目标函数可以表述为：

(4)

(5)

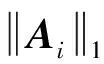
(6)

公式(6)中αij，αik表示系数向量αi的第j、k个元素。该指标与重构的相对误差能量呈现显著的正相关关系。

训练样本的SPI指标由该样本的稀疏重构系数矩阵计算得出，可以在任何现有字典训练算法基础上独立进行，因此从理论上讲，现有算法都可以通过将SPI作为约束条件，使之具备从根本上优化重构矩阵稀疏性能、并进一步减小误差的能力。

2.2 利用稀疏性能约束的K-SVD算法

K-SVD算法的求解模型基于l1范数，通过对重构系数向量绝对值之和的限制来实现稀疏求解。K-SVD算法的约束条件如(7)所示。

(7)

通过这样一个约束条件，把NP难的l0范数求解转化为一个针对重构误差的凸优化问题。在建模初始阶段，一部分样本可能由较多的成分组成，导致字典初始化不够充分，而导致重构系数能量趋于分散时，l1范数难以使这些重构系数能量趋于聚拢、实现稀疏，进而在整个学习过程中，稀疏字典都无法有效的针对这些样本进行学习，不能提取这些样本的真实成分，只能使用更多的现有成分进行拟合；这直接导致了上文所提现象的产生，即算法倾向于给出由更多与成分不相等的原子，而非完整成分构成的稀疏解，从事件相关电位分析的角度来看，无法提取出能够更精准描述ERP波形的字典原子，也就是说EPR波形会分布在较多的字典原子中，这些样本未能有效参与到字典的学习过程中，没有做到将样本帧分解为具有实际意义的信号源。

原始K-SVD 算法的约束条件为重构信号与原始信号的误差，我们将SPI加入到目标函数中，如公式(8)，使SPI是否足够小也作为一个字典训练阶段的约束条件，当训练进行过程中，同时优化，如果SPI达到了一个极小值，即迭代过程中变化可以忽略时，则停止训练。如果SPI已经不发生明显变化，根据SPI的定义，说明样本的完整成分已经集中在几个原子之中，对于ERP样本来说，代表ERP波形的主要成分已经包含在字典原子波形中。

(8)

SPI作为约束条件的物理意义是指，在代表特定成分语境下，能量在字典原子中的集中程度。与LASSO不同之处在于，SPI考虑到了同样L1范数下，稀疏分布的不同情况。加入了SPI的稀疏约束项，比传统LASSO更精密。

3 方法验证

3.1 数据集选取

本文选取了一个公开的EEG数据集。该数据集记录的是基于听觉P300的拼写器的测试数据。该数据集由Höhne等人[16]于2010年公开。实验数据由若干个trial组成，每个trial包括9个声音刺激，每个刺激之间间隔120 ms。实验数据包含两种刺激：目标刺激和非目标刺激，比例为1∶8。在原数据集中，代号为nw的被试顺利的完成了实验中的全部trial，同时原论文中，nw的EEG数据分类准确率最高。所以本文选取原始数据集中代号为nw的被试数据作为示例。

3.2 数据预处理

第1步：分帧。

本文介绍的方法需要在分帧之后的数据上进行。本文按照数据集的实验设计进行分帧。以每个声音刺激事件发生的时间作为分帧的时间起点，选取之后的800 ms作为帧长，分帧时间终点就是每个声音刺激呈现之后的第0.8 s，舍弃trial之间的脑电数据。帧长的选取与原数据集论文的ERP分析相一致，即与声音刺激有关的ERP成分波形出现在800 ms以内。显然，这样的分段会产生比较多的重叠。这一点会在后文中的聚类结果体现出来。采样率为150 Hz时每帧包含120个数据点。

第2步：能量归一化。

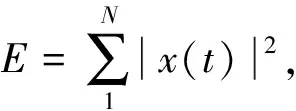
第3步：聚类分析。

作为一种稀疏分解算法，本方法获得的字典必然是过完备的，很多字典原子会具有相似的性质或者波形。因此在获得稀疏字典之后，下一步需要对字典原子进行聚类操作。考虑到本方法是一种非监督分析方法，字典原子的种类是未知的，因此本文选取利用自组织映射网络进行非监督聚类，来找到字典原子分类个数的极大值。

本方法中，字典原子时域向量直接作为自组织网的输入层，训练获得网络经过训练之后，再次将字典原子送入，即可获得聚类结果。

4 结果

4.1 稀疏性能指标

稀疏性能指标SPI的结果如图1所示。可以看出，SPI会随着实验进程发生变化，表明SPI可以在一定程度上代表EEG的变化。

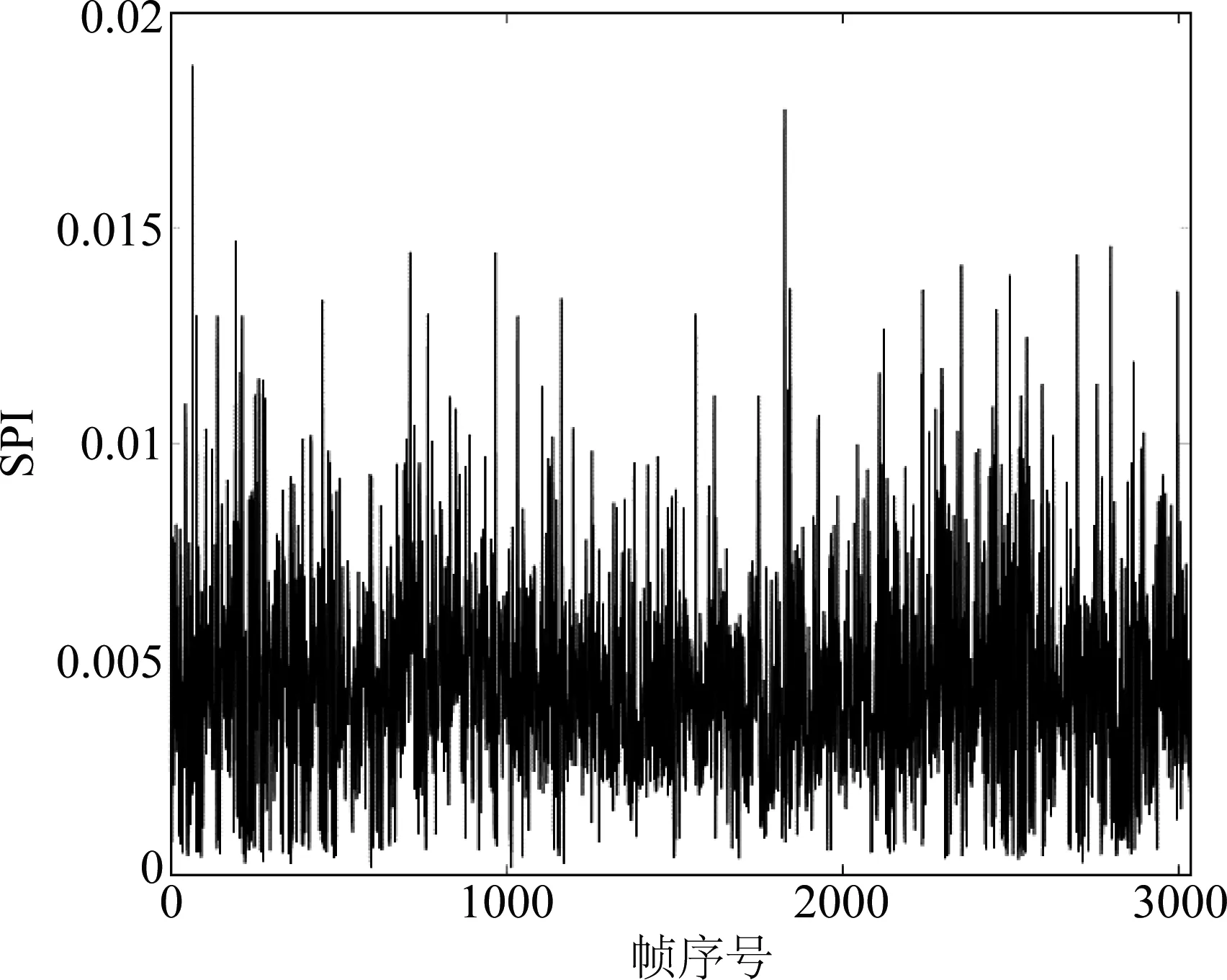
图1 每帧的SPI。横坐标为按时间排序的帧序号Fig.1 SPI of every frame. Horizontal axis is frame index ordered by time course

4.2 原子聚类结果

图2为SOM聚类之后，每类包含的样本数。可以发现字典原子聚类之后，绝大多数原子都聚集在10类中，原子之间时域上的相似性被很好的发掘出来。

4.3 原子聚类后波形

图3为每个类中的原子的平均波形和叠加平均后的目标刺激ERP，可以看出，有4个原子类都体现出了目标ERP波形，而且样本数据中由于分帧和实验设计产生存在的具有相位延迟的ERP波形也被提取出来。我们计算了叠加平均后的ERP波形与原子波形之间的互相关。结果显示，图3(b)中的原子波形与ERP波形在0相差时相关性最强，达到0.8，图3(c)中的原子在有相位延迟的情况下达到了0.6。互相关结果说明本文的方法达到了提取ERP波形为字典原子的目的。

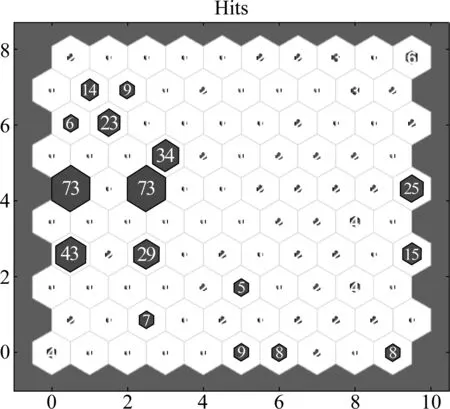
图2 SOM聚类命中图Fig.2 SOM hits diagram

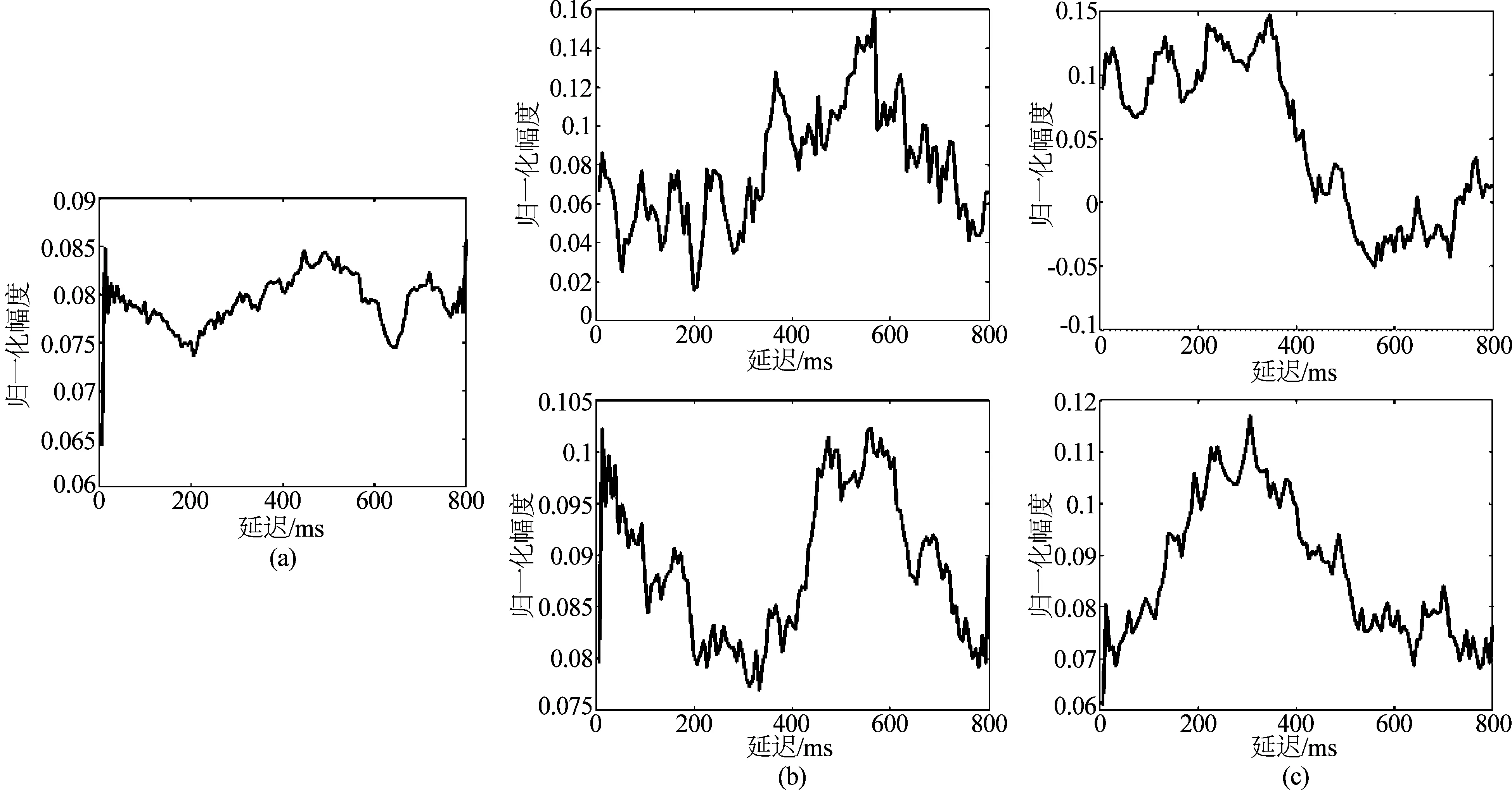
图3 (a)所有目标刺激的叠加平均后ERP波形,(b)与ERP波形接近的字典原子类平均波形,(c)与ERP波形有相位延迟的字典原子类平均波形Fig.3 (a) Averaged target ERP waveform, (b) Averaged ERP-like waveform of dictionary atoms clusters, (c) Averaged phase-delayed ERP-like waveform of dictionary atoms clusters

4.4 基于稀疏表示系数的样本分类结果

为了验证本方法的有效性，我们利用对分帧之后的脑电数据分解获得的稀疏表示系数进行原数据集论文中所述BCI识别操作。我们使用了513维的分类特征，其中包括512维的稀疏表示系数和一维的SPI。样本标记分为两类，一类是该帧起点播放的是目标刺激，另一类是该帧起点播放的是非目标刺激。我们选取了SVM作为分类器进行二分类识别。总共3303帧样本中，二分类准确率为78%。该发布数据集的论文中，使用了来自全部64个通道的数据，获得了80%准确率。而本方法只使用了1个通道的数据也获得了近似的结果。

5 结论

本文设计了一种新的EEG信号稀疏分解方法来提取事件相关电位中的有效成分，并通过在公开数据集上的实际应用，证明该方法是有效的。

与基于匹配追踪的稀疏分解方法相比，本方法训练得到的稀疏字典具有明显的生理学上的含义，可以更精准可信地利用稀疏系数来表示EEG信号中所包含的信息。在本文中也通过实验证明，仅仅通过单通道EEG数据求解字典和系数，即可实现单次ERP提取。

本方法中，字典原子的长度与信号帧等长，训练过程也是以信号帧为单位进行，因此不同的分帧方法会对结果产生影响。这一点在前文结果展示部分有所体现：不同的延迟的ERP波形会训练出多种不同延迟的字典原子。因此本方法在应用时会受到实验设计与分帧方法的双重影响。

而对于分帧方法的依赖使得用本方法分析任意的EEG数据时难以获得稳定的结果。而对于事件相关电位的研究来说，如果以事件开始的时间作为基准点，只需选取一个固定的帧长就可以获得稳定的分帧结果，因此本方法应用在ERP研究时通过选取一个固定的帧长度即可在不同来源数据之间获得稳定的结果。