改进CSP算法的联合特征优化法

张学军 黄婉露 黄丽亚 成谢锋

(1. 南京邮电大学电子与光学工程学院，江苏南京 210023;2. 南京邮电大学射频集成与微组装技术国家地方联合工程实验室，江苏南京 210023)

1 引言

脑机接口(Brian Computer Interface, BCI)通过大脑神经活动产生的信号控制外部设备，例如：机械手臂、轮椅等[1-2]。通常BCI设备包含信号采集、预处理、特征提取、特征分类、信号转换、反馈控制外部设备等基本元素[3]。根据信号采集过程中使用传感器的类别，BCI系统可以分为：侵入式和非侵入式两种。

非侵入式BCI系统由于其低损害性和高便捷性受到研究者们的青睐，其采集的信号多为低损耗、高时间分辨率的脑电图信号[4]。采集到的脑电信号中会包含眼电伪迹、心电伪迹和肌电噪声等，需要通过信号预处理去除不相关信号分量保留有用信息。在特征提取过程中，经过预处理后的信号更容易形成高判别性的特征集，常用的有：时域特征集[5]、频域特征集[6]、时频特征集[7]、自回归特征集[8]、空间特征集[9]等。为了使分类器更有效地解码使用者的大脑意图并且将其转换为可以控制外部设备的输出信号，一部分提取到的特征被用于训练分类器，进而增强分类器的性能[10]。目前，基于EEG(Eectroencephalogram, EEG)的BCI系统面临诸多挑战，发掘有效的特征提取方式、改进机器学习技术，使之能够提高BCI系统的时频分辨率、空间分辨率、鲁棒性以及在线适应能力。因此，不断改进信号处理方法、模式识别技术以及优化分类器在该领域地位举足轻重[1]。

特征提取算法的优劣将直接影响模式识别结果的准确性，是BCI系统中至关重要的环节。常用的特征提取方法可分单一域和混合域两类，其中，单一域又可以分为时域、频域、空域。空域分析法例如传统的公共空间模式(Common Spatial Pattern, CSP)分解，能够在一定程度上提高信噪比，文献[11]中运用CSP算法进行运动想象任务的脑电信号特征提取。然而，脑电信号包含大量信息，复杂程度较高，仅仅在单一域分析并不能很好地表征信号的特征。因此，YANG Banghua等[12]提出结合小波包分解(Wavelet Package Decomposition, WPD)和CSP的方法提取运动想象脑电信号。文献[13]结合频域和空域，提出稀疏时频段下的共空间模式算法，该算法能够在时频段上自动地选择具有判别性的特征。

传统的CSP算法产生一个空间滤波器，其性能取决于频率，一般需要设置一个大范围的频带或手工选择一个特定的频率范围。为了解决这个问题，文献[14]提出了滤波器组公共空间模式算法，用于自主执行重要时间-空间特征的选择。Pavel Merinov等人[15]将上述的滤波器组扩展运用到神经网络中，基于特征创建线性分类器，从而解决特征的优化问题。文献[16-17]提出加权正则化CSP算法，该算法根据每位被试的实验数目进行加权，计算每个通道的有效系数，减少不需要的通道。文献[13,18]中提出增强型CSP特征提取，利用频率互补特征映射选择制约频带间的相关性，从多层分解的频带中提取CSP特征，最后采用卷积层与各子采样层交替的卷积神经网络(Convolutional Neural Networks, CNNs)层次结构进行深度学习和深层分析，达到模式分类的目的。文献[20]综合近年来的研究热点，改进CSP滤波器，提出结合经验模式分解(Empirical Mode Decomposition, EMD)和CSP 的特征提取算法。

本文基于文献[20]提出基于CSP的联合特征优化方案：首先运用S变换(Stockwell Transformation, ST)对CSP空间滤波器进行改进，改进后的CSP算法称为基于S变换改进的CSP算法(Common Spatial Pattern based S transform, CSPS)。然后将CSPS分别结合总体经验模式分解(Ensemble Empirical Mode Decomposition, EEMD)、双谱特征两个方面提出特征提取优化方案，分别构建EEMD-CSPS、双谱-CSPS特征。最后进行特征降维，并采用支持向量机(Support Vector Machine, SVM)、线性判别分析(Linear Discriminant Analysis, LDA)分别进行模式识别，其中SVM选取不同内核参数进行调整。实验数据分析结果表明，综合时间复杂度和分类正确率后，采用双谱-CSPS进行特征提取，LDA算法进行特征分类的结果，相较于文献[20]提出的改进算法有了较为明显的提高，在BCI竞赛数据集中，本文算法提高约4.73%，最大增量为7.23%，平均系统响应时间从0.19 s缩短到0.12 s；在实验数据集中，本文算法提高5.67%，最大增量为6.08%，平均系统响应时间为0.22 s。

2 数据集描述

本文采用两个数据集：BCI Competition 2008 data sets 2b的竞赛数据[13]和本实验室获取的实验数据，前者在文献[20]中已经做了详细描述，下面主要介绍实验室自采数据集。

实验数据集采用本实验室Neuroscan系统采集，包含3位被试的EEG数据。3位被试均为男性，平均年龄25岁，右利手，有正常或者矫正正常视力，为了描述方便并与BCI竞赛数据作区分，现将三位被试编号为：A01、A02、A03。所有被试均坐在扶手椅上，坐姿要求端正，注视前方电脑屏幕，屏幕距离双眼水平距离约为1 m。数据集被试编号如表1所示。

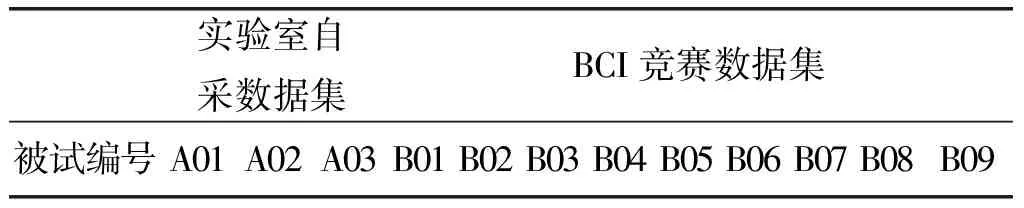
表1 各数据集列表

如图1所示，每个被试数据采集过程分为三段，每段间隔2分钟，用于被试调整姿势、精神放松。每段实验中包含20组想象任务，每个小组任务持续时间约为7 s，具体流程如图2所示。

图1 实验总体分段图Fig.1 The diagram of experiment sections

实验范式包括四个阶段，在思维任务阶段被试进行左右手想象运动中，想象左右手握拳、打开运动。

实验范式涉及两种提示：“→”表示想象左手运动，“←”表示想象右手运动，任务标签“1”表示左手运动；任务标签“2”表示右手运动。

被试准备阶段：从第0 s开始，0～2 s为放松状态，屏幕全黑，在此期间，被试者不进行任何想象任务，处于闭眼放松状态。

提示阶段：第2 s时，屏幕中央显示“+”，同时伴有提示声音，提示被试者准备进行想象任务，此时被试者睁眼，注视“+”；第3 s时，屏幕中央随机出现“→”“←”(左右)箭头提示符号，符号显示0.5 s后消失。

思维任务阶段：符号消失后，被试随即闭眼，集中注意力按照箭头方向进行肢体运动想象任务，想象任务时间持续3.5 s。

放松阶段：实验结束，休息10～15 s，进入下一轮实验。

每一类范式的实验分为3组，第1组为训练组，后两组为测试组，一共进行300次实验，所有试验均在一天内完成。在10～20系统中，C1、C3、C5、FC3、CP3、C2、C4、C6、FC4、CP4覆盖了位于大脑中央前回的感觉运动皮层区域，所以本实验采集12个通道的信号，包括：左半球C1、C3、C5、FC3、CP3和右半球的C2、C4、C6、FC4、CP4以及参考电极Cz和VEO，其中VEO用以记录眨眼动作，以便预处理中更好地去除眼电伪迹。

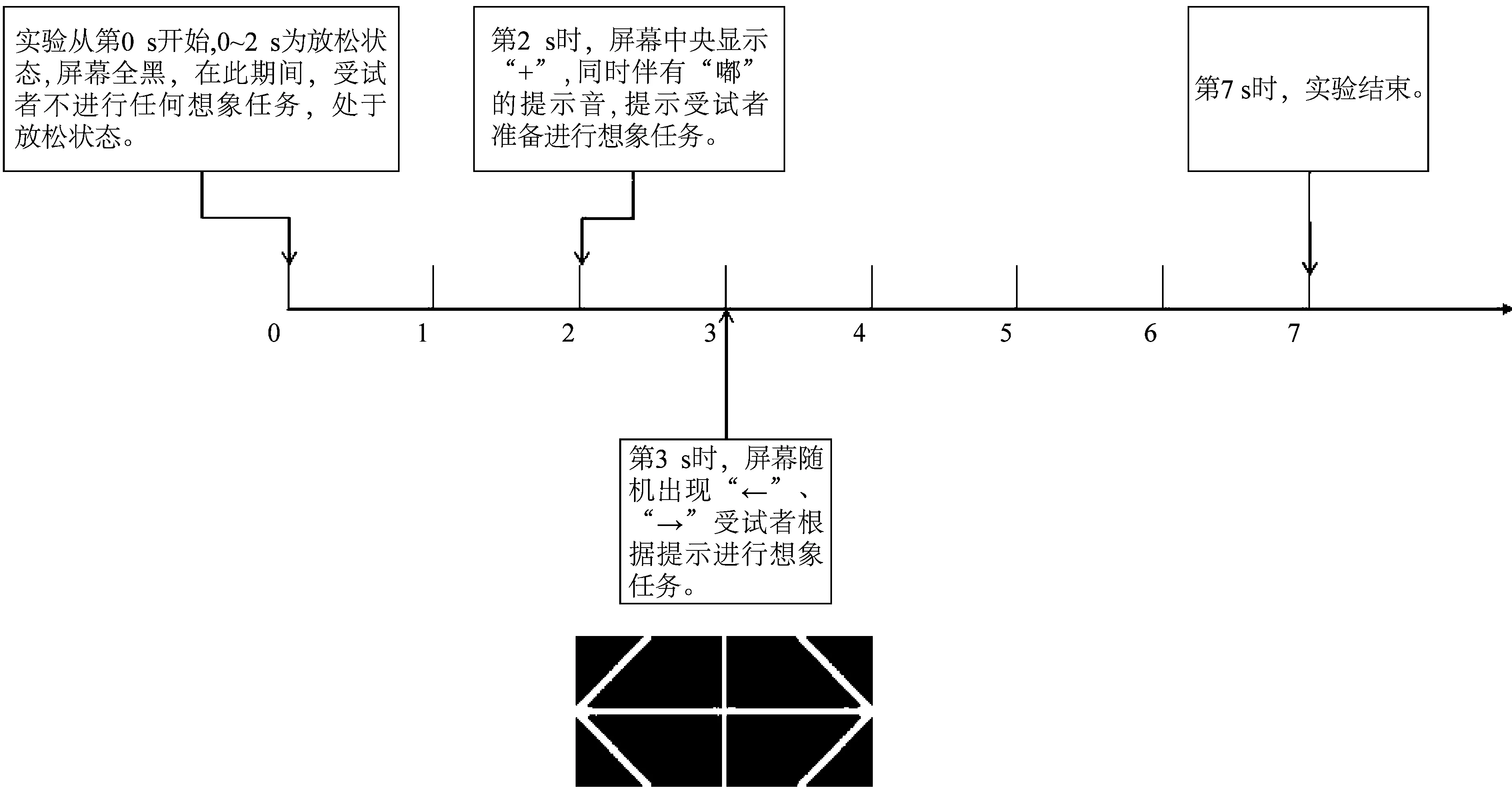
图2 实验设计时序图Fig.2 The diagram of experiment operation

3 基于S变换的空间滤波器

3.1 S变换

S变换由R.G.Stockwell在1996年提出，是一种具备频率独立分辨率的时频表示方法[3]。一方面，该算法发展了小波函数，具有相位因子，可以对小波变换进行“相位校正”，各频率分量的相位谱与原始信号保持直接的关系，另一方面，S变换在短时傅里叶变换(Short-Time Fourier Transformation，STFT)的基础上，采用宽度与频率倒数成正比的高斯函数作为窗函数进行分析，改善窗宽固定的缺陷[19]。

(1)连续S变换

在连续的S变换中，信号函数x(t)∈L2(R)的一维连续S变换定义为

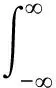
(1)

S变换的反变换为：

(2)

S变换本质上是由傅里叶函数加窗后得到。窗函数以τ为中心，标志出函数在变换时时间轴上的位置。窗函数与频率f相关，窗的宽度随着f不断变化，比STFT的固定窗宽有了明显的改善作用。同时S变换中相较于原始的小波变换采用相位因子ej2πfτ进行相乘运算，能够实现小波函数的相位校正。S变换综合了短时傅里叶变换和小波变换的优点，改进了二者的不足，是一种具有良好操作性能的时频分析方法。

从式(1)中可以看出，S变换由x(τ)e-j2πfτ和|f|e-πt2f2卷积而成。对两个部分分别进行傅里叶变换，即可得到频域上的S变换表达式：

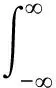
(3)

(2)离散S变换

实际采集的脑电信号往往是离散的电信号，要从这些信号中提取左右手想象的特征信号，需要对采集信号进行离散数据的S变换。

在频域的S变换表达式(3)中，令t=ΔT，f=mΔF，α=pΔF，可以得到离散的S变换表达式为：

(4)

其中，ΔT代表采样时间间隔，而ΔF指出了抽样频率。

S变换步骤为：

步骤1 采集脑电信号，得到一组离散的时间序列值x(kT)，(k=0,1,…,N-1)，其中T为采样间隔，N为采样点数。

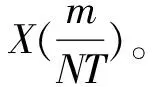
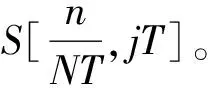
快速S变换结合了FFT和时域卷积的优点，使在短时间内得到一个准确地S变换结果，对于工程应用有着极为显著的优势。

3.2 基于S变换的公共空间滤波器成分选择算法

基于S变换的公共空间滤波器成分选择算法步骤为：

步骤1 将滤波后的信号经过EMD得到各固有模态函数(Intrinsic Mode Functions, IMFs)。

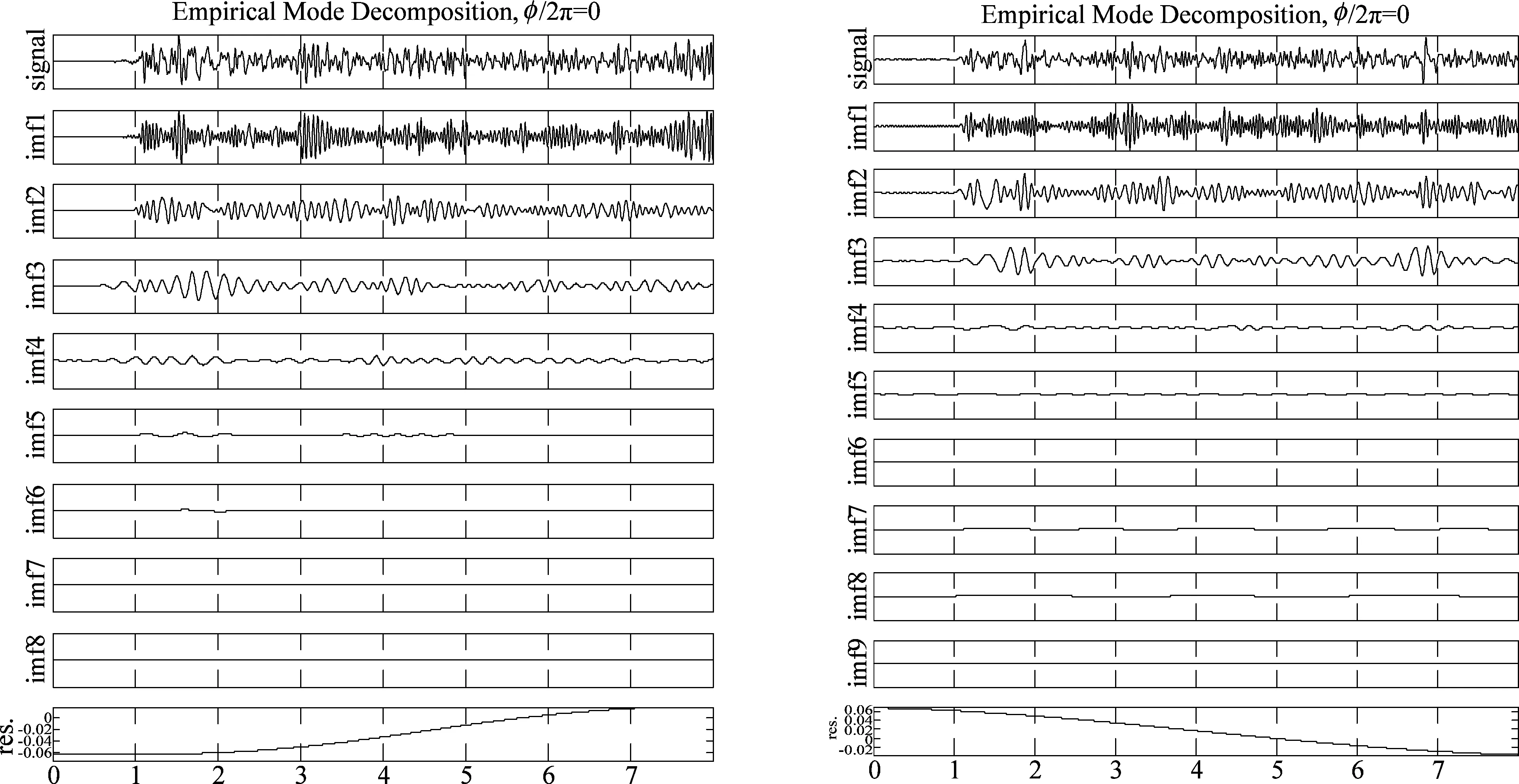
图3 受试B01右手想象运动信号EMD分解图(左图：C3通道，右图：C4通道)Fig.3 EMD of B01 right-hand motor imagery in one trial(Left:C3 channel, Right:C4 channel)

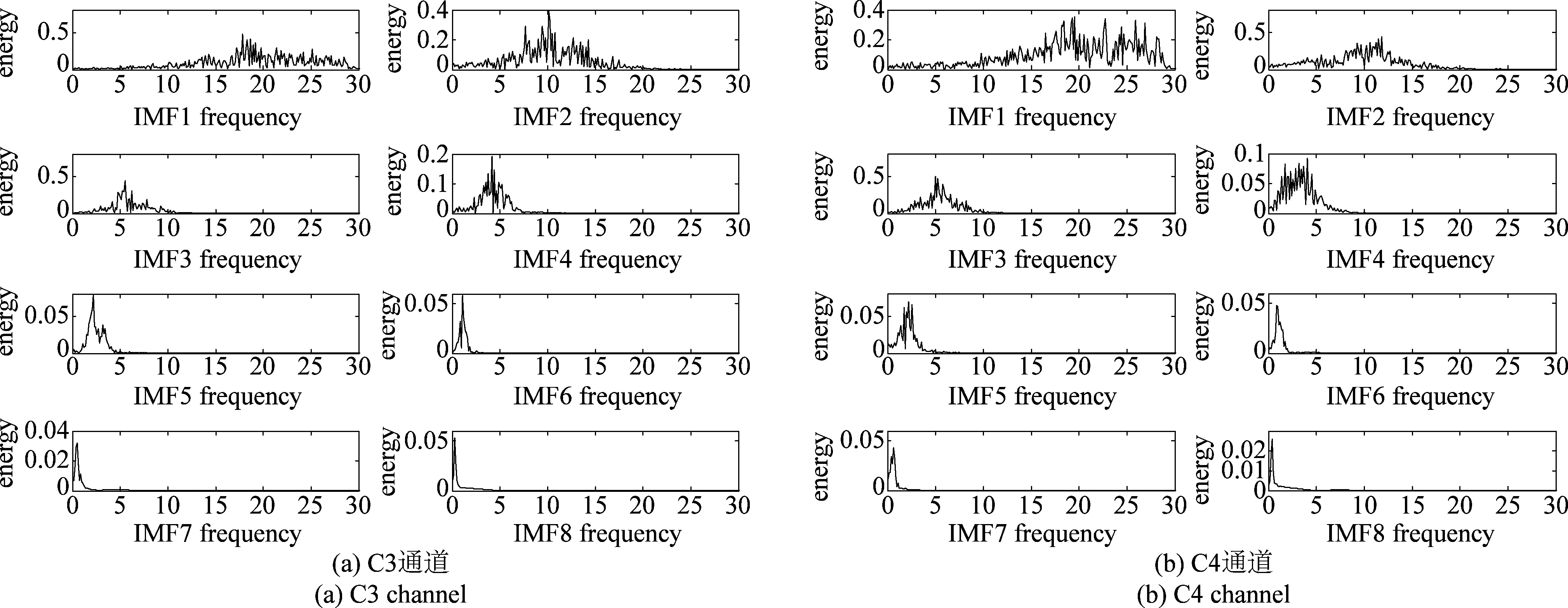
图4 想象右手运动前8阶IMF分量能谱图Fig.4 IMF power spectrum of right-hand motor imagery

步骤3 对G1和G2向量矩阵分别进行CSP分解，具体过程见文献[20]，其中采用S变换进一步优化CSP滤波器W，成分选择算法的步骤为：

a)使用对EEG信号进行EMD时采用的结合CSP算法的特征提取过程进行计算，选取所有的特征向量组成空间滤波器W；

c)计算Data2中六个通道数据的S变换谱值，其中包含C3通道前三阶IMF分量和C4通道前三阶IMF分量，选取每组训练集中不同类别之间S变换值差异最明显的前三对分量对应的特征向量，构成新的滤波器W′。

步骤4 对Data1用滤波器W′进行再次滤波，滤波后的数据为Data3。

步骤5 最后通过SVM进行分类。

3.3 特征有效性验证

图5为单次trial的C3、C4通道脑电信号在CSP滤波后进行S变换得到的能谱图，横轴为一个trial包含的2000个采样点，时长8 s，纵轴为频率。颜色的深浅表示电极信号的活跃度，即能量大小。由图可见，一方面，S变换谱明暗分明，表明在进行运动想象思维任务时间范围内信号特征较为活跃(图中亮色区域)，在运动想象间歇期信号特征较弱(图中暗色区域)；另一方面，在进行左右手想象运动时，C3通道活跃的位置对应C4通道处于低活跃度状态，符合想象运动中的时间相关同步/去同步现象(Event-Related Synchronization/Event-Related Desynchronization, ERS/ERD)。

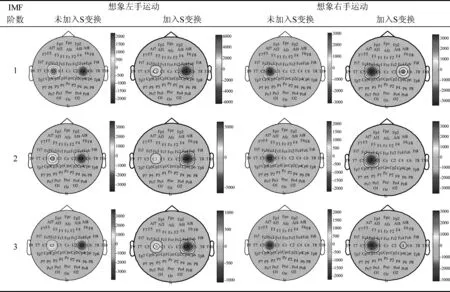
为进一步验证该特征的有效性，将文献[20]中改进CSP滤波后特征的脑地形图与加入S变换后特征的脑地形图进行比较。表2为加入S变换前后，被试B01单次trial的脑电信号EMD分解后前三阶IMF分量经过CSP滤波后特征的脑地形图，一方面，加入S变换前后的脑地形图均表现出与运动想象中时间按相关同步/去同步特征相符合的通道活跃性，加入S变换前后得到的特征均可以有效表征出“源”的空间位置信息。另一方面，值得注意的是，在S变换前后特征差异明显度的表征上，由表2中进行想象左手运动时得到的C3、C4通道特征，在进行S变换后的能量差异更加明显。值得一提的是，在其他8位被试中，也发现了同样的现象。由此可以推测，在进行S变换后，特征的判别性增强，下文将通过特征分类的结果来证实该推断。

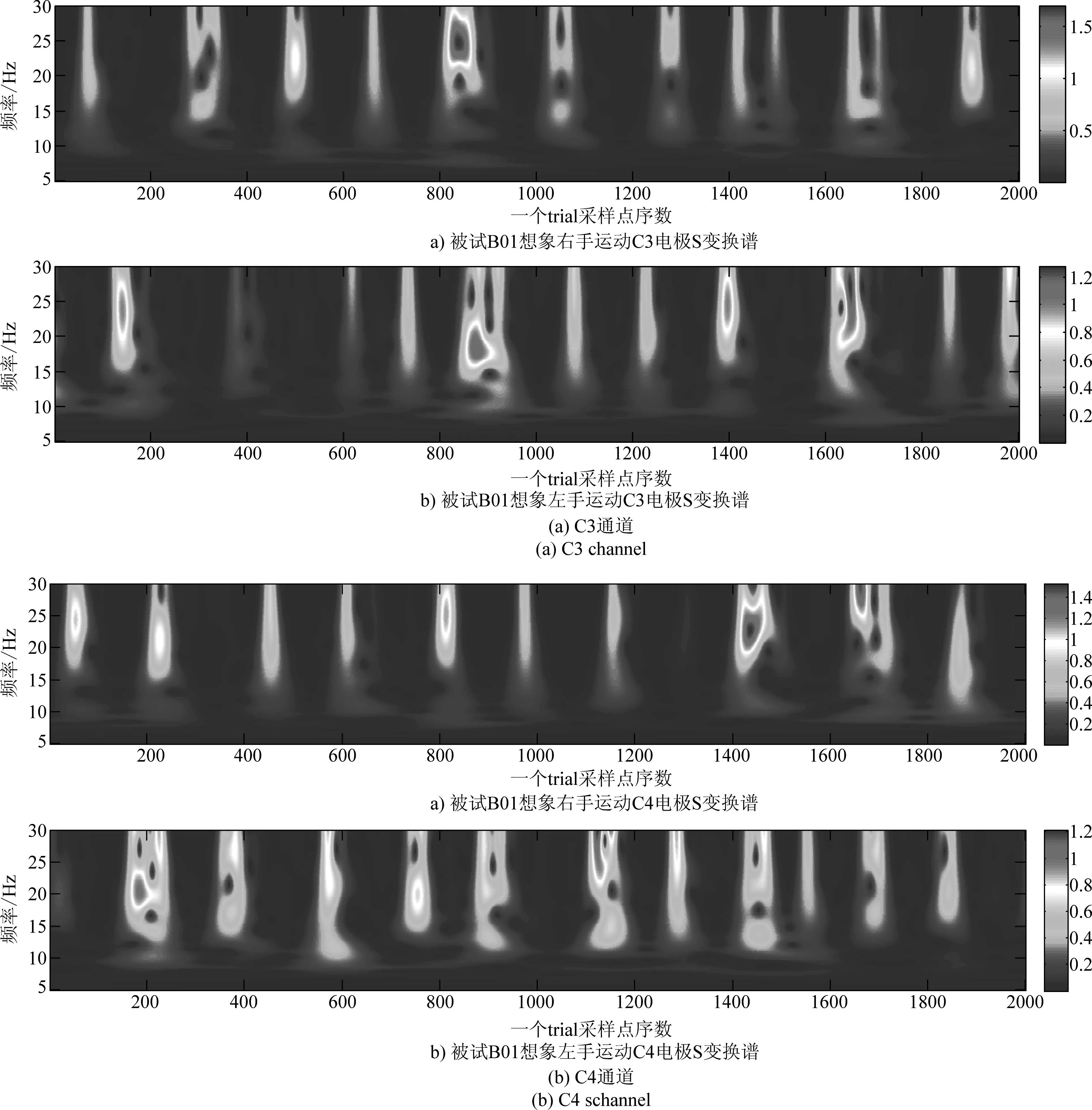
图5 被试B01单次S变换频谱图Fig.5 S-transform spectrogram of B01 in one trial

4 CSP的联合特征

4.1 优化方案

方案1 在文献[20]提出的改进CSP滤波器成分选择算法基础上，结合CSP和EMD的特征提取方法，获得EMD-CSP特征。

方案2 在方案1的基础上，加入S变换优化滤波器的特征提取方法，获取EMD-CSPS特征。

方案3 在方案2的基础上，将EMD算法部分换成EEMD，获取EEMD-CSPS特征。

方案4 在方案2的基础上，将EMD算法部分换成双谱估计，获取双谱-CSPS特征。

4.2 EEMD-CSPS联合特征

(1)EEMD

EMD具有模态混叠现象，主要表现为两个情况：一个IMF中包含差异极大的特征时间尺度、相近的特征时间尺度分布在不同的IMF[21-22]。为了克服模态混叠问题，Wu等人提出了EEMD，即总体平均经验模式分解法[23-24]。

EEMD在原始信号的基础上加入分布在整个时频空间的高斯白噪声，则原始信号和噪声重构成一个“总体”。加入的噪声与被滤波器分离得到的不同尺度分量一致，当信号加在这些一致分布的白色背景噪声上时，不同尺度的信号便会自动映射到合适的参考尺度上。由于高斯白噪声零均值的特点，在平均后包含的剩余噪声越小，结果就越接近真实值[25]。

具体的EEMD步骤如下：

步骤1 确定总体平均的次数K，本文设K为25。

步骤6 重复步骤2至5，直到i等于K。

(5)

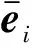
(2)EEMD-CSPS特征提取过程

在S变换后的算法基础上，我们将CSP算法结合EEMD算法，构成新的EEMD-CSPS联合特征，并与EMD-CSP算法进行比较，探究分类性能的改善情况。

具体EEMD-CSPS联合特征提取优化方案步骤为：

步骤1 将滤波后的信号经过EEMD分解得到各固有模态函数(IMF)，其中迭代次数设置为100。

步骤2 通过计算每个IMF的能量谱筛选在μ节律和β节律(5～28 Hz)的振荡模态，将多个IMF看成新的多通道信号。

步骤3 对多通道信号通过CSP分解，通过CSP算法滤波后数据进行S变换，在不同类别状态下S变换谱的差异选取空间滤波器的构造成分，构造新的空间滤波器，获取特征向量组。

步骤4 采用支持向量机(SVM)分类器对特征进行分类。

(3)EEMD-CSPS的频段筛选

原始信号经EMD和EEMD变换后得到如图3、图6(a)所示的IMF分量，选择竞赛数据中被试B01第一个trial中想象右手运动信号为例，每一个IMF分量代表一种振荡模式，包含了相应的频域信息。选取前8阶IMF分量，求能量谱。图6(b)为想象右手运动C4通道前8阶IMF分量的信号能谱图。可以看出，在5～28 Hz内，IMF1-IMF4的能量较为集中，IMF5-IMF8则可能为低频高能量的肌电信号。由此，选取IMF1-IMF4问题进一步CSP特征提取；另外，结合图3、图6，比较EMD和EEMD结果可见，采用EEMD得到的IMF信号能量更强，受噪声干扰较小，各模态更加清晰。

4.3 双谱-CSPS特征

(1)双谱分析

双谱作为阶数最低的高阶累积量谱，是三阶累积量的二维傅里叶变换，现在已经被广泛运用于信号处理，应用范围涉及雷达、通信、振动分析、电磁学、生物医学、天文学等多个领域。

对于平稳随机信号x(t)，令k=3,x1=x(t),x2=x(t+τ),x3=x(t+τ),可得随机信号x(t)的3阶距为：

m3x(τ1,τ2)=E{x(t)x(t+τ1)x(t+τ2)}

(6)

零均值随机信号的三阶矩和三阶累计量相等：

c3x(τ1,τ2)=m3x(τ1,τ2)=E{x(t)x(t+τ1)x(t+τ2)}

(7)

由式(7)可以看出，平稳随机过程的三阶累计量中只有τ1，τ2两个变量。则K阶累积量谱即为K阶累计量的K-1阶傅里叶变换。由此可得：双谱即为三阶累积量的二维傅里叶变换，对式(7)进行二维傅里叶变换可得双谱函数：

(8)

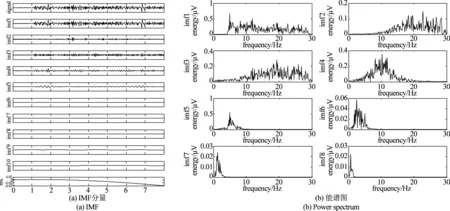
图6 想象右手运动C4通道前8阶IMF分量和能谱图Fig.6 IMF and its power spectrum of C4 right-hand motor imagery

双谱一般为复数，并且是周期函数，具有如下的对称性：

Bx(ω1,-ω1-ω2)=Bx(-ω1-ω2,ω1)=

Bx(ω2,-ω1-ω2)

(9)

(2)双谱估计

双谱估计分为直接法和间接法，直接法跟功率谱估计中的周期图法相似，即首先计算数据的傅氏变换，然后做频域相关，具体步骤为：

步骤1 设数据集({x(k)},k=1,2,…,N，分成K段，每段有M个样本，记作：xi(0),xi(1),…,xi(M-1),i=1,2,…,K，分段可设重叠，当不存在重叠区域时，N=KM。

步骤2xi(n)为第i段样本数据，对每段数据进行傅里叶变换，可得：

(10)

步骤3 计算DFT系数的三重相关，即得到每段数据的双谱估计：

Xi(-λ1-λ2-i1-i2)

(11)

式中，0≤λ2≤λ1，λ1+λ2≤fs/2，Δ=fs/N0,fs为采样频率，N0和L1需要满足关系式：M=(2L1+1)N0。

步骤4 对上一步的结果求平均，即为样本数据的双谱估计：

(12)

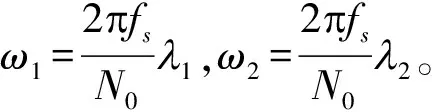
5 特征识别过程优化

5.1 SVM的内核参数优化

文献[20]详细地介绍了SVM的工作原理，并且采用线性、惩罚因子C=7的支持向量机对提取的滤波特征分类，核参数γ和误差惩罚因子C是影响SVM性能的主要参数。γ的取值影响空间变换后的数据分布，惩罚因子C则决定了支持向量机的收敛速度及推广能力，本文从改变惩罚因子参数和引入核函数两个方面来优化SVM的参数模型。

(1)参数选择

惩罚因子C选择：7、7.5、8、8.5、9、9.5、10 七个值，采用BCI2008竞赛数据集进行分析，通过比对分类正确率和系统分类时间两个维度，筛选出C的最优参数区间为[9,10]。

(2)核函数选择

基于惩罚因子C取值在[9,10]，对BCI2008竞赛数据集分别采用线性、多项式、径向基三种核函数实验发现，采用线性内样的SVM分类正确率最高。不同参数下，分类正确率虽然存在差异但整体差别较小，在竞赛数据集分类正确率在93%～96%之间，实验数据集分类正确率则在82%～86%之间变化。

5.2 LDA

LDA寻找某一向量使得Fisher准则达到极大值，在该投影方向上，类间离散度最大、类内离散度最小，称此方向为最佳投影方向，训练样本在最佳方向投影后，得到最强的分离性。

本文将在联合特征优化的基础上，采用LDA分类方法对所提取的联合特征进行分类，并与参数优化后的SVM分类结果比较。

6 结果与分析

本节分别从加入S变换改进CSP算法、构建关于CSP的联合特征、特征识别过程三个角度结合对BCI竞赛数据集和实验数据集进行比较，并将分类正确率和分类识别时间作为优化方案的评判标准，探究各方案的有效性并选择最优方案。

6.1 改进CSP滤波器优化结果与比较

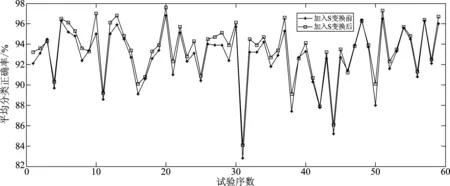
图7 被试B01加入S变换前后单次trial分类正确率比较Fig.7 The classification accuracy of B01 in one trial with/without S transform

B01B02B03B04B05B06B07B08B09平均值未加入S变换92.7693.4589.4693.3791.490.4493.8889.7192.2691.86加入S变换93.4693.7590.2693.8792.891.5494.1890.9193.1692.66平均增量0.70.30.80.51.41.10.31.20.90.8

下面采用基于S变换的改进空间滤波器对实验室自采实验数据进行处理，采用未优化的SVM进行特征分类的结果如表4所示：加入S变换后，3位实验被试的想象运动信号分类结果均有所提高，表现为与BCI竞赛数据集基本相同的规律，值得关注的是，实验数据集的增量比BCI竞赛数据集的增量大。由此，进一步证实加入S变换的优化方案具有可行性和有效性。在下文的优化方案中，默认采用加入S变换改进后的CSP空间滤波算法进行特征处理。

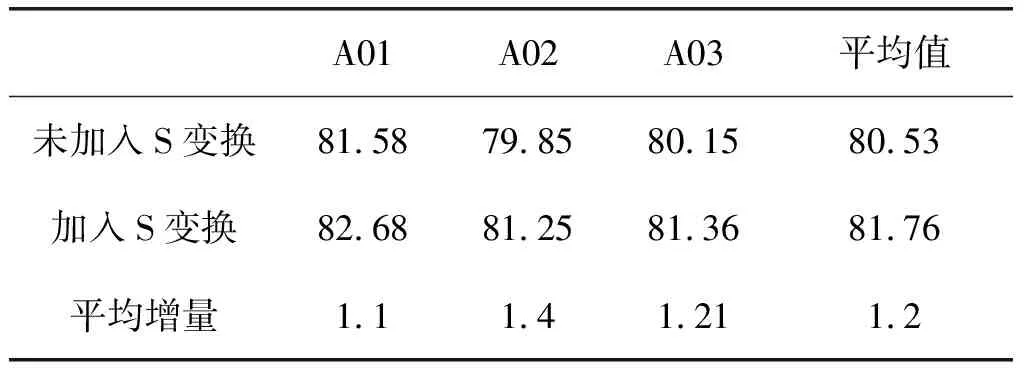
表4 3位被试S变换前后所有试验平均分类正确率对比表(实验室自采数据集)

6.2 CSP联合特征提取算法比较

下面对4.1节的4种优化方案从分类正确率和时间复杂度两个方面进行比较。

(1)分类正确率

图8、表5分别为4种方案下，BCI竞赛数据中被试B01单次trial和9位被试所有试验，采用未优化的SVM进行特征分类的平均分类正确率，可以看出方案4整体的分类正确率要高于其他3个方案；结合表4中9位被试在4种方案下具体的正确率和方案4分别与其他3个方案之间比较的所得的正确率增量值，可以看出方案4在方案3的基础上，又将正确率均值提高了1%；另外，与表5中方案3的优化效果相比，方案4所得到的准确度增量更多，其中，与最初方案1的分类结果相比，增量均值约2.6%；此外，结合图表，我们可以发现，该方案在被试B03和被试B08，较方法1分别提高了3.6%和4.1%；较方法2分别提高了2.6%、2.9%，较方法3分别提高了1.1%、1.7%。因此，初始分类结果不理想的被试运用该方法获得的优化效果更明显，即优化方案对分类正确率较低的被试效果更好。

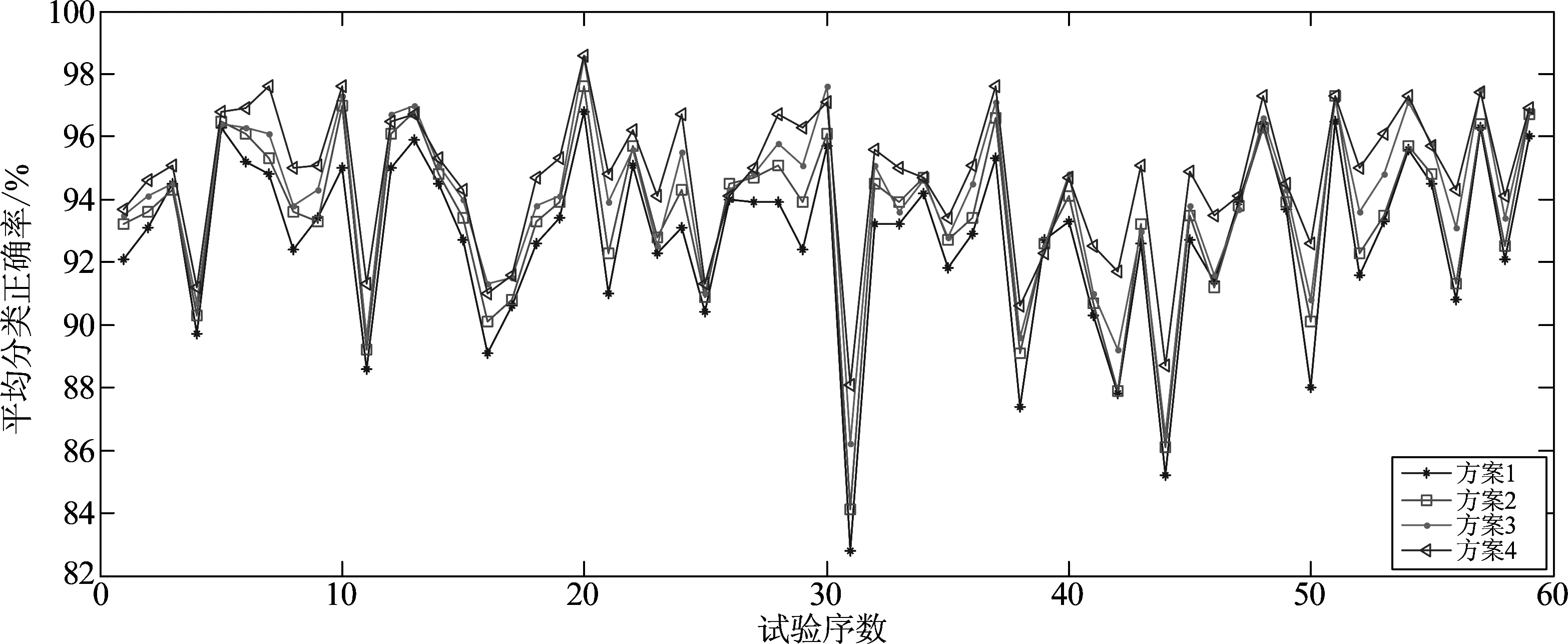
图8 被试B01 4种方案单次trial分类正确率比较Fig.8 Classification accuracy of B01 in one trial with 4 different methods

方案1分类正确率方案2分类正确率方案3分类正确率方案4分类正确率方案4与方案1增量方案4与方案2增量方案4与方案3增量B0192.7693.4693.8894.782.01.30.9B0293.4593.7594.2595.351.91.61.1B0389.4690.2691.9693.063.62.81.1B0493.3793.8794.1795.271.91.41.1B0591.4092.8093.6094.703.31.91.1B0690.4491.5492.8494.143.72.61.3B0793.8894.1894.3894.680.80.50.3B0889.7190.9192.1193.814.12.91.7B0992.2693.1693.9694.362.11.20.4平均值91.8692.6693.4694.462.61.81.0

表6为实验室自采数据集中3位被试4种方案下的正确率数值(采用未优化的SVM进行特征分类)和方案4分别与方案1、方案2、方案3的增量值，可以看出第4种方案与其他3个方案的比较增量较为明显，其中，最高增量均值为4.3%(与方案1相比)，被试A02的分类正确率增量最大，与方案1相比增加4.9%，与方案2相比增加3.5%，与方案3相比增加1.7%，进一步验证了在竞赛数据集分析中得到的推断：优化方案对分类结果较低的被试优化效果越明显；与表5相比，该方法在处理实验数据集时的优化效果更为明显。

(2)时间复杂度

时间复杂度主要衡量系统分类过程所耗费的时间。表7所示为4种特征方案下两类数据集进行特征分类的响应时间对比，由表可见，无论是竞赛数据集还是实验数据集，方案4都具有最短的响应时间和最小的响应时间偏差(方案1竞赛数据集和实验数据集的响应时间偏差分别为：0.0089，0.0133；方案4竞赛数据集和实验数据集的响应时间偏差分别为：0.0059，0.0111)。

6.3 特征识别过程优化结果与比较

下面运用LDA分类方法对所提取的联合特征进行分类，并与参数优化后的SVM分类结果比较，如表8所示。

表6 3位被试4种特征提取方案所有试验的平均分类正确率和增量对比

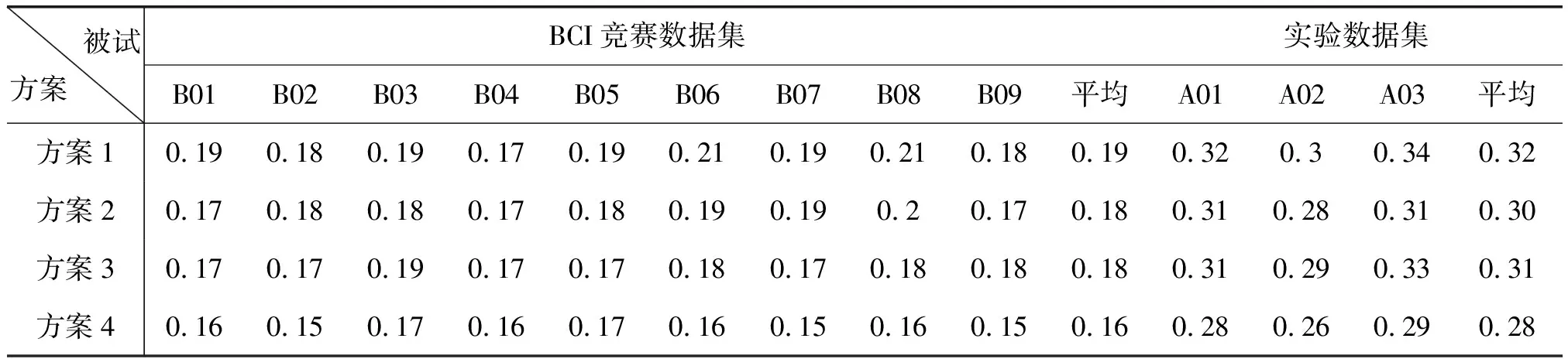
表7 4种特征提取方案下系统响应时间对比

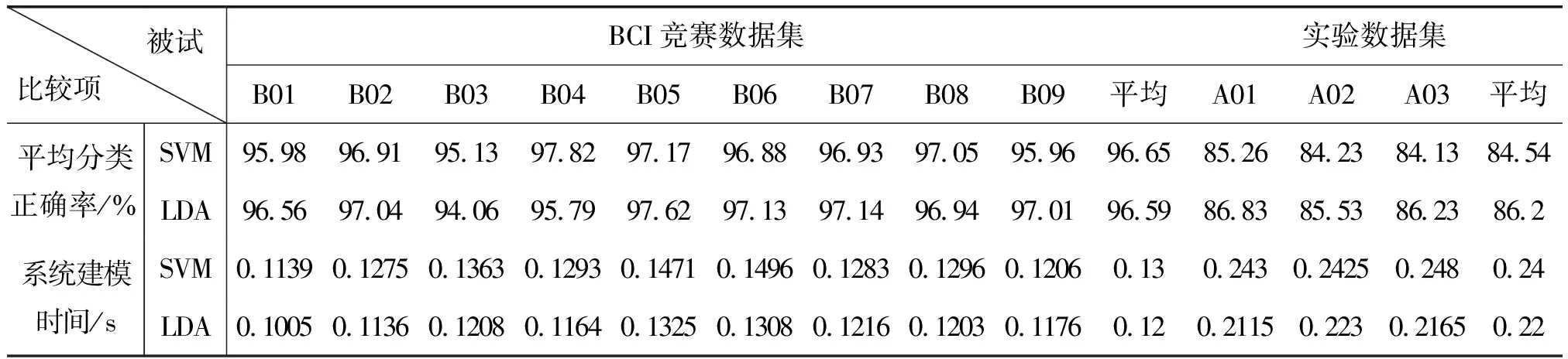
表8 2种分类方法分类正确率和系统响应时间对比

除B03、B04两位被试外，其余10位被试的分类结果中，LDA的分类正确率更高，说明LDA对该特征的分类效果要优于SVM。进一步结合表8分析可得：在竞赛数据集分类效果原本已经较优的情况下，LDA的平均分类正确率高出SVM结果约1%；在实验数据集中，LDA算法优势更加明显：在分类正确率均值高出SVM分类器约1.7%的同时，系统响应时间降低了0.02 s，此外，对于原本分类正确率较低的实验数据集，LDA对分类性能的提升较竞赛数据集更加明显。因此，在分类正确率稳定性差不多的情况下，LDA所用的系统建模时间要短于SVM，平均减少约0.01 s。

7 结论

本文对文献[20]提出的改进特征提取方法进一步优化，采用自采实验数据集和BCI竞赛数据集进行特征提取和分类识别。从CSP滤波器优化、联合特征优化以及识别过程优化三个方面，探究特征优化的有效性。实验结果表明：S变换优化CSP滤波器后，构建的基于双谱-CSPS的联合特征结合LDA分类器的识别方法，获得较高的分类正确率和较低的系统建模时间，在实验数据集中平均分类正确率达86.20%，响应时间0.22 s，在竞赛数据集中平均分类正确率达96.59%，响应时间0.12 s。本文实验数据集分类正确率普遍低于竞赛数据集，说明实验设计和信号处理方面还有提升的空间。