脑电信号成分稀疏分析范式及其可行证明

岳 琪 徐忠亮 马 琳 李海峰

(1. 东北林业大学信息与计算机工程学院，黑龙江哈尔滨 150040;2. 哈尔滨工业大学计算机科学与技术学院，黑龙江哈尔滨 150001)

1 引言

自1993年被Mallat和Zhang提出以来，稀疏分解(压缩感知)技术作为一种可靠的信号处理与传输方法，在包括EEG的各类时变信号、各类图像的分析和处理及故障诊断领域得到了广泛的应用[1-5]。该方法可以通过学习得到样本集相关的稀疏字典及样本对应的稀疏系数向量，以实现对信号内在成分结构的解析，去除噪声成分[6]，并得到不依赖待处理信号的事先假设(如FFT的短时时不变假设，ICA的独立性假设)、且具有相对较高的稳定性(相对EMD产生的模态混叠[7]及端点效应等[8])的分解结果。

稀疏分解算法的典型应用涵盖图像、音频等多类信号的压缩存储[9]，对统计独立噪声的消除[10]，信号分析相关的事件或成分探测[11]，基于信号探测阵列的信源方向或阵元位置校正[12]等。 在以上这些应用领域中，信号压缩存储与去噪更多依赖信号样本集的整体统计特性，对成分分析精度要求不高；但在信号成分分析相关的应用、特别是EEG信号的解析中，稀疏分解算法经常只能得到比真实成分更零散的原子基底，从而无法得到精密的分析结果。类似的现象也在ICA、EMD等算法中呈常态出现，体现为不同成分间线性相关部分互相包含[7- 8]，而非呈现为完整、单一成分的波形。这种情况大大影响了EEG分析的效率与精准度，严重限制了对其进行成分分析的效果。由于篇幅所限，本文不对ICA、EMD等算法进行深入讨论，只对稀疏分解算法进行分析和探讨。

目前最广泛应用的稀疏分解算法以K-SVD字典学习算法[13-14]、OMP回归分析算法等为代表，其求解模型基于l1范数，通常把l1范数视为一个稀疏约束条件，将l0范数求解转化为一个针对重构误差的凸优化问题进行求解。这样的求解方式会带来一些问题，即当一部分样本初始稀疏建模的系数能量由于各种原因趋于分散时，l1范数难以使这些样本的重构系数能量趋于聚拢、实现稀疏，稀疏字典也无法提取这些样本的真实成分；这直接导致了上文所提现象的产生，即算法对这些样本给出的稀疏解与真实成分不符，对它们的成分提取和分析是失败的。

事实上，若能将l0范数有效的连续化，并纳入稀疏求解模型中，重构系数能量分散的情况将会得到极大的改善。在之前的工作中，我们观察到了l1范数求解模型影响奇异样本重构结果的一些实验现象，对其进行了初步解释，并提出了一个可用于对样本内部成分分布情况进行度量的稀疏性能评价指标SPI(Sparse performance index)；在本文中，我们将对该指标进行更新，讨论它作为一个连续的优化对象代替离散的l0范数约束项的可能性，并对包含该指标(或其他l0范数的近似替代)的求解范式进行探讨，论证其在脑电信号分析的实际应用中，令字典基底有效拟合训练样本集中实际成分的可能性。

2 改进的稀疏性能评价指标(SPI)与其替代l0范数约束项的可能性

使用字典D对样本yi进行稀疏分解，有以下通用表示：

yi=Dai+e

(1)

式中D={d1,d2,d3,…,dM}，每个原子dj长度为L；yi=(yi1,yi2,yi3,…,yiL)T，ai=(ai1,ai2,ai3,…,aiM)T表示第i个样本及其重构系数向量；ei=(ei1,ei2,ei3,…,eiL)T表示该分解结果的重构误差。包含l0范数的稀疏分解问题已被证明是一个NP难问题，故在实际应用中通常使用l1范数代替l0范数，此时稀疏分解迭代求解模型可以表示为：

(2)

(3)

实际计算中通常把l1范数视为约束条件，以把该NP难问题转化为凸优化问题进行求解。然而引言中已经提到，这种近似求解模式会导致不同样本的初始及最终稀疏模式不同，对其进行分解的效果不一。为了准确度量单一样本分解结果的稀疏性能，我们提出了重构系数向量的稀疏性能指标SPI[15]，利用系数能量分布对稀疏性能进行度量。经过参数和值域调整，该指标被重新定义如下：

(4)

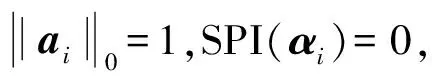
(5)

(6)

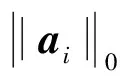
相对于传统模型，该模型多了一个优化对象即SPI指标，包含该指标的双目标优化模型不是凸模型，需要使用模拟退火等全局竞争性优化方法进行求解。这会带来一定的计算资源消耗的提升，但相对于单纯以误差作为优化对象的传统算法，将能有效防止稀疏度的过度增长和稀疏模型的碎片化，从而得到更稀疏、原子更接近样本集内真实成分的解。接下来，我们将对优化模型的收敛域及字典原子收敛情况进行讨论，并通过实验进一步验证这一观点。

3 包含l0范数或其近似约束项的稀疏求解问题的最终收敛域

在本节中，我们将对满足稀疏性假设，即每个单一样本恰好具有τ个实际非零成分(τ<0.05M)的充分完备的样本集，根据其建模稀疏度τ′与实际稀疏度τ的相对关系，分三种情况讨论其稀疏分解模型。

为了便于讨论，不妨假设真实成分之间的差异都显著大于成分的随机震荡。不妨设：

(7)

1.当τ′=τ，探讨误差期望Eei的极值：对随机部分ri的复原误差期望，任意两两线性无关的向量组都是相等的；故当误差期望Eei取得极小值，即系统收敛至τ′=τ情况下的全局极小时，样本的确定部分必然能被τ′维向量组线性表示，即有：

(8)

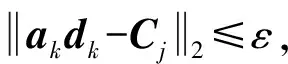
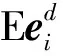
(9)

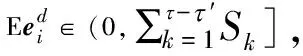
(10)

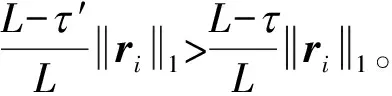
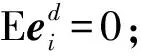
(11)

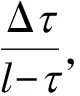
综上所述，对于一个由误差期望Eei与稀疏度限制τ构成的双目标等权值优化问题，在τ′=τ处事实上生成了一个对该问题组合最优解的吸引子。该吸引子处不仅可以得到误差-稀疏限制双目标组合优化问题的最优解，还可以得到盲源分离问题的一组较精确的基底，用于样本集内或集外同质信号的分析。接下来，我们将通过仿真与实际信号的分解实验来证明这一观点。

4 实验结果与分析

4.1 SPI指标与奇异样本分布的相关性

在该部分实验中，我们将对真实脑电信号进行稀疏分解，并将不同样本帧根据其稀疏性能指标进行排序，根据其误差分布探讨其内部成分的分布与传统方法分解结果的问题。实验数据来自柏林工业大学的听觉数字ERP脑电数据集[16]，降采样至150 Hz，共30000帧长120采样点的EEG数据，512维字典12稀疏度进行分解。实验结果如图1所示。

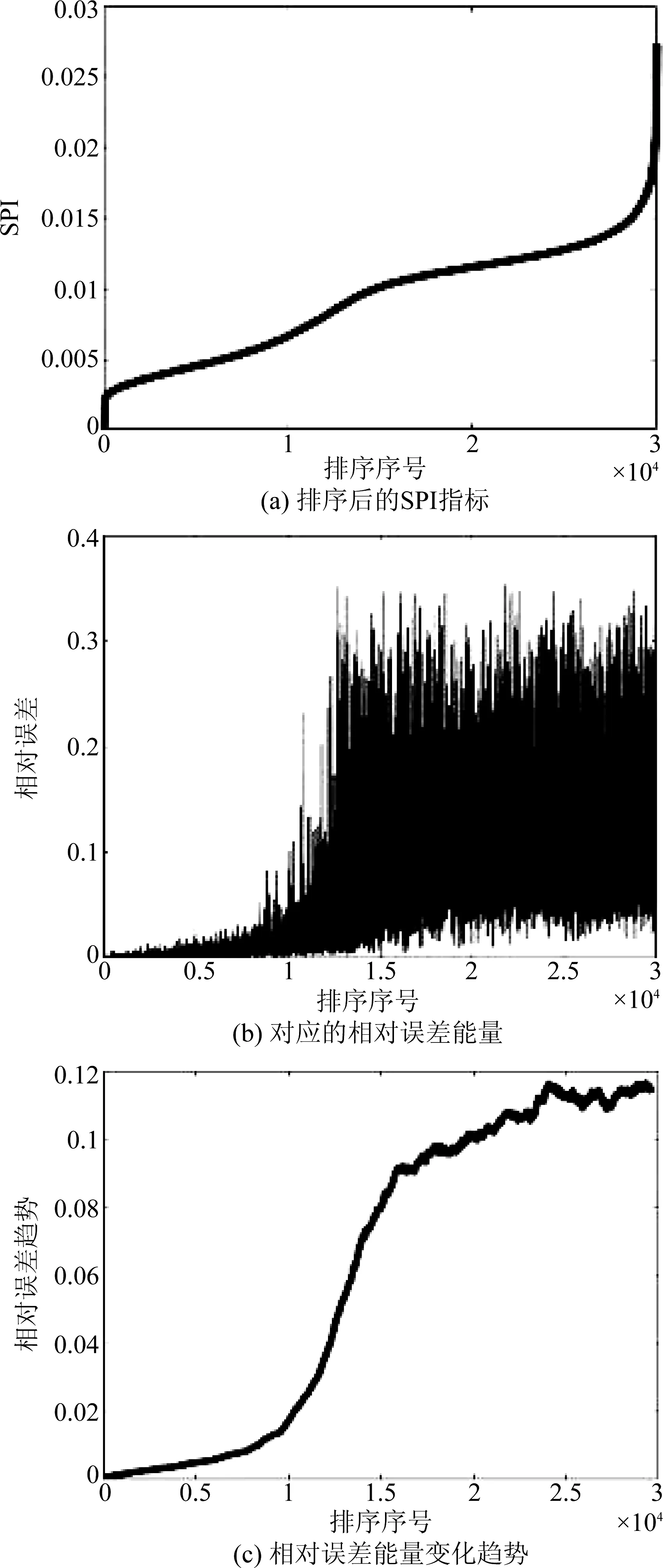
图1 EEG信号与SPI指标相关的分析结果Fig.1 EEG signal analysis results related to SPI

可以看到，当分解结果中的实际SPI达到一定阈值并开始快速上升时，对应的平均误差能量也开始快速上升，表明稀疏性能较差的样本复原效果也较差。在这部分样本中相对误差能量分布范围非常广泛，其中误差相对较低的部分尚可以解释为样本本身复杂程度更高从而导致误差稍高；然而大量的样本相对误差能量超过了15%，这只能解释为这些样本无法在字典中精确匹配到相称的原子，且这一现象在整个学习过程完成后都未消失，意味着传统优化范式学习得到的字典在对部分样本(稀疏性能最好的33%)进行针对性学习的同时未能兼顾其余样本，从而造成大量稀疏性能较差样本的复原效果也差、对其进行的成分分析也没有实际意义。

4.2 包含SPI的优化能量函数在稀疏度限制域上的分布情况

在该部分实验中，我们首先构建了256×320维的人工信号基底集,由5～32 Hz的方波、正弦波、三角形波、高斯/Hanning窗函数及这些波形的低频移相信号、高频幅度调制信号构成。使用这些基底集构建训练样本集，每个训练样本由不同强度的τ个字典基底构成，添加能量相当于训练样本2%～5%的白噪声形成人工训练样本集。对该样本集在不同稀疏度限制下进行多次重构，统计其重构误差、分别以l0范数和SPI作为稀疏约束的能量函数分布情况和两个稀疏约束的相关关系。包含误差与稀疏限制的能量函数方面，我们将误差与稀疏约束分别归一化至0～1区间并相加作为该能量函数的值以确保二者在优化过程中等效。实验结果如图2～图4所示。

图2 τ=3时对分解效果的平均统计结果Fig.2 Average statisticaltatistical results of the decomposition results at τ=3

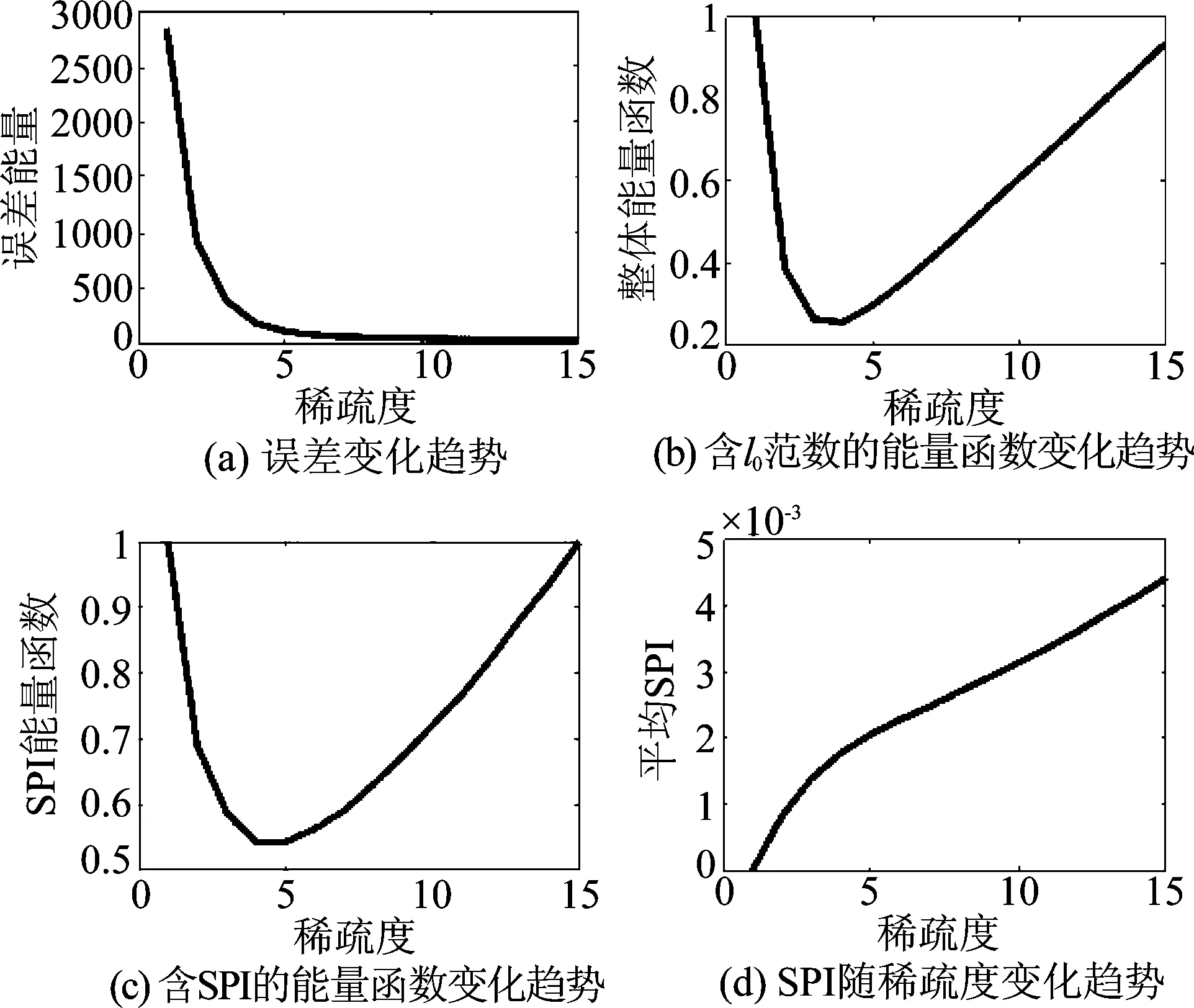
图3 τ=4时对分解效果的平均统计结果Fig.3 Average statisticaltatistical results of the decomposition results at τ=4

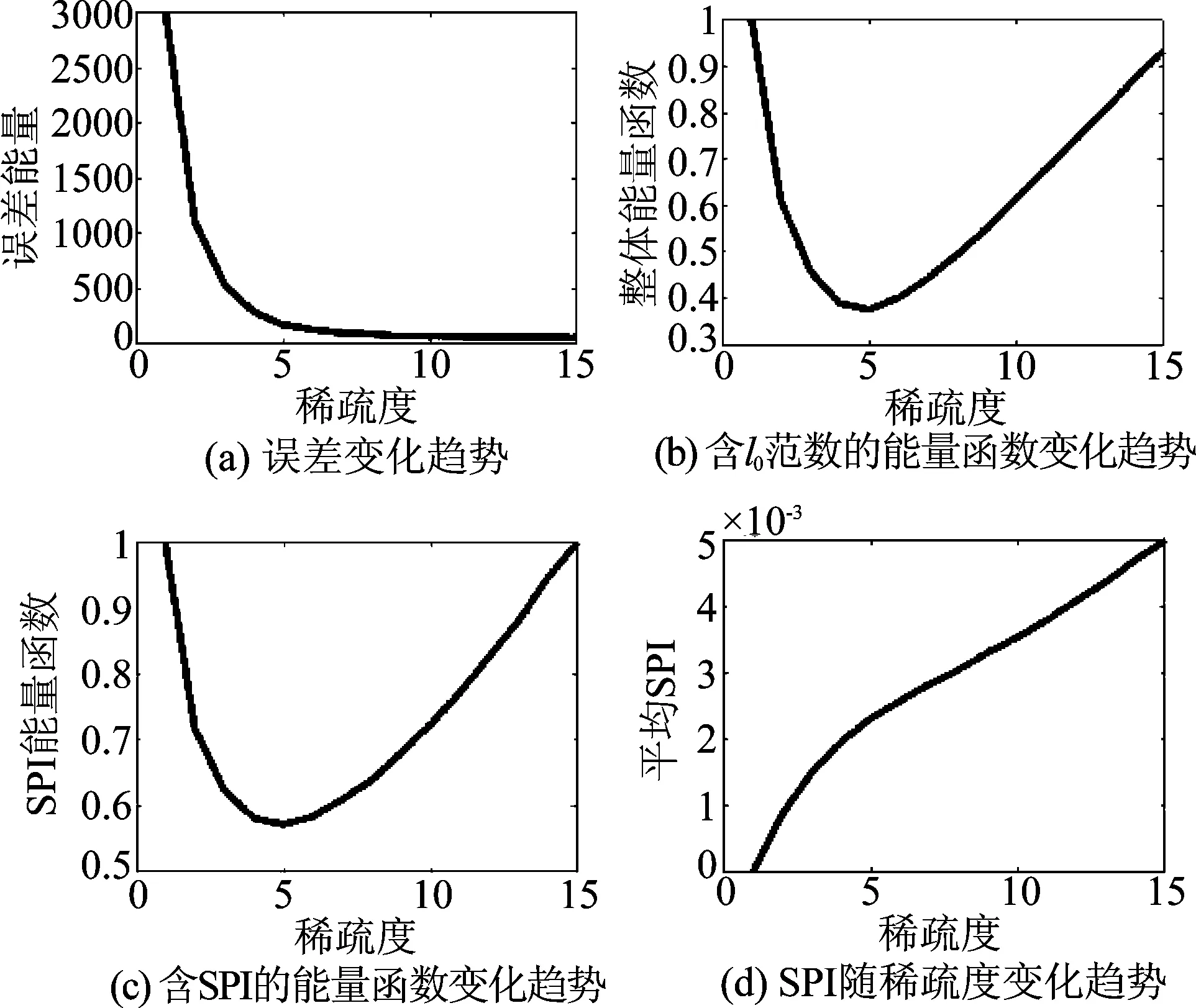
图4 τ=5时对分解效果的平均统计结果Fig.4 Average statisticaltatistical results of the decomposition results at τ=5

可以看到，包含l0范数和SPI的能量函数基本相同，且吸引子同样较精确地存在于真实成分数处；l0范数(即真实稀疏度)与平均SPI近似线性相关，证明了二者在优化过程中基本等效。当稀疏限制τ不断提升，模拟信号中的成分之间产生相关的可能性也更大，从而无法精确保证样本中有τ个独立的真实成分，使实验的直观结果失去意义，故模拟实验的稀疏度限制到τ=5为止。

结果表明随稀疏度提升，重构误差单调降低，而结合稀疏度与SPI的能量函数值在τ附近得到最低点，事实上在样本集内部实际不相关成分数处形成了一个吸引子；若以该能量函数作为优化目标，系统最后必收敛于该位置，得到与信号真实不相关成分数目相同的分解结果。相对的，传统范式的优化对象即误差会在优化过程中不断趋向于降低，从而使稀疏建模的稀疏度增大至算法允许的极限，一方面使字典原子波形无法逼近真实成分、另一方面也使建模的稀疏性能变差。接下来，我们将使用真实EEG信号进行同样的验证。实验采用的数据集与第一部分相同，实验结果如图5所示。

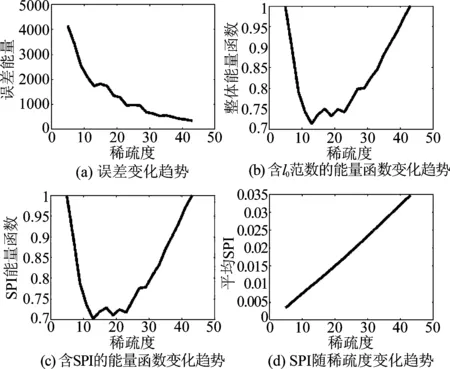
图5 ERP相关脑电信号分解结果的平均统计结果Fig.5 Average statisticaltatistical results of the ERP related EEG signals

可以看到，实际EEG信号中，两个能量函数依然存在着显著的吸引子；事实上，考虑到该EEG数据集的性质(ERP诱发实验)，吸引子存在的位置(12，19)应分别与静息及诱发波时段的真实独立成分数量比较接近。同时，在稀疏度限制接近真实情况时，平均SPI指标与真实稀疏度呈现相当严格的线性相关关系，验证了在真实情况下用SPI指标来实现l0范数近似求解的可靠性。同时，传统范式优化对象(误差)的趋势与模拟实验并无差别，有力地证明了两个范式在对样本集拟合能力方面的差异性。

在本部分实验中，我们使用模拟信号及真实EEG信号验证了稀疏指标(绝对稀疏度或SPI)与误差的联合能量函数中吸引子的存在，并且验证了其与真实成分数量的相关性，同时通过分别包含l0范数和SPI的能量函数的形态以及二者的直接相关性证明了SPI与l0范数在优化过程中的等效性，这些事实可以为我们的观点提供有力支持，即结合误差与l0范数或SPI构成的稀疏求解范式与传统范式存在着显著的收敛域差异，可以有效地避免建模中稀疏度不受控增长及由此导致的字典原子和样本系数模型散碎化，使分解算法收敛于样本集真实成分的分布、实现接近该分布的信号解析。同时SPI作为l0范数的一个有效连续近似，能够替代l0范数作为稀疏约束项，从而实现任意步长的稀疏-误差联合优化——同时也是l0范数问题的更精确的近似求解过程。

5 结论

本文面向EEG成分分析的实际需要，给出了经过改良的稀疏性能评价指标SPI，利用该指标进行稀疏分解中的奇异样本分析，并对其作为l0范数的近似约束项的可能性进行了理论分析，在传统稀疏优化范式基础上给出了利用该指标进行稀疏字典学习及稀疏建模的范式并探讨了该范式的收敛情况。实验证明，稀疏性能评价指标SPI与重构误差结合，可以较好地鉴别不同类别训练样本集中的奇异样本，同时加入了SPI指标的稀疏分解求解范式可以较好地逼近训练样本集中的实际成分数量，并对训练样本集的真实成分进行更可靠的拟合。在对以SPI指标作为近似l0范数约束项的稀疏求解范式进行可靠的工程实现后，可以在训练样本充足的情况下对EEG成分进行解析，提取脑电信号真实成分波形并发现可能的未知诱发信号，并基于训练所得稀疏字典进行同质信号的解析，对EEG及其他复杂时变信号的处理及分析具有相当程度的价值。