基于Wiener强度退化过程的机械零部件可靠性灵敏度分析*

李 臻，尚 伟

(1.四川交通职业技术学院 汽车工程系，成都 611130；2.东北大学 机械工程与自动化学院，沈阳 110819)

0 引言

在机械设计中，可靠性计算的应用已经对机械零部件的强度设计、失效研究、材料选择等部分产生了较多的有益影响，对提高结构设计效率起到重要作用，其计算结果也成为评价产品质量的重要依据。同理在机械部件和系统维护的过程中，可靠性设计对系统的运行开发和维护都有重要指导意义。

1956年Birnbaum[1]提出的应力-强度干涉模型，成为现代可靠性设计的经典理论模型。经过60年的发展，许多学者都在此基础上进行了大量的研究和发展，并推导出更多的计算模型。其他统计方法和力学方法如矩方法、摄动法也应用到可靠性分析中来[2-6]。

随着研究的深入，静态的可靠性设计方案已经不能满足复杂的使用情况的要求，人们需要考虑更多的因素以描述精确的可靠度表达式，对产品的可靠性评估也更加苛刻。将时间因素引入可靠性分析，计算时变可靠度，考虑强度退化因素成为其中一个研究方向。

在应力-强度模型基础上计算时变可靠性的方法主要有3种：将应力描述为随机过程、将强度描述为随机过程、将应力与强度都描述为随机过程。

机械产品的可靠性灵敏度分析能够在计算结果中体现产品的随机因素对系统可靠性的影响水平大小，从而在设计过程中能够通过干预这些敏感因素来提高整体的可靠性[7-9]，因此在可靠性设计和可靠性优化过程中分析可靠性灵敏度是必要的。

本文的结构设计先对通用的考虑强度退化的可靠性模型进行推导，然后使用螺栓为研究对象进行理论的应用，在计算中得到其可靠度及可靠性灵敏度数值并进行分析，以提高其可靠性。

1 可靠性计算与验证可靠性设计理论

可靠性分析是通过由功能函数的概率分布来求出功能函数的失效概率，而功能函数的统计规律是由基本随机变量的统计规律决定的。

结构的功能函数(状态函数)用式(1)表示：

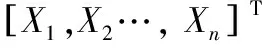
(1)

式中，R表示强度向量，S表示应力向量，X表示随机变量，n表示随机参数数量。

一次二阶矩方法[10]是将非线性的功能函数展开成线性功能函数，计算出动能函数的统计特性。进而得到可靠性指标，可以求出可靠度。

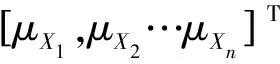
(2)

则功能函数的均值和标准差为：

μZ=gX(μX)

(3)

(4)

功能函数gx(x)对基本随机变量X求一次偏导数得到：

(5)

由式(3)和式(4)计算可靠性指标如式(6)所示：

(6)

可靠度为：

(7)

失效率为：

Pf=1-R

(8)

式中，Φ代表标准正态分布函数。β与可靠度在数值上是对应的，在物理意义上也有对应关系。具体表现为β的大小与可靠度成正比关系。蒙特卡洛设计(Monte Carlo simulation)[11]的基本理论是建立在概率论大数定律基础上的，使用这种方法得到的可靠度结构比较精确。用其计算结果与其他方法对比可以进行误差的矫正。设抽样组数为N，每组随机变量计算得到的功能函数值为Zi，Zi≤0的次数为L，则在大批抽样之后，结构的可靠性由下式计算：

(9)

R=1-Pf

(10)

2 Wiener退化过程建模

产品的性能退化过程本质上是一个随机过程，且产品的性能退化是由很多微小损失量的累积所造成的均匀而平缓的退化过程，假设用Wienner过程描述产品的强度退化，可以保证强度退化的随机性，在采用一元 Wiener 过程建模中，退化量逐渐变大，即产品强度只能是逐渐减小的，保证了强度退化的单向性，并且具有良好的计算分析性质，因而成为目前基于性能退化的可靠性建模与分析中最基本、应用最广的模型之一[12-15]。一元 Wiener 过程适用于在时间历程一系列微小增量的损伤累积进行建模，例如机械零件的疲劳、腐蚀和裂纹扩展等。

产品性能的退化是一个均匀且缓慢的过程，是由大量的微小的损失量逐渐累积造成的。Wiener过程是目前工程实际中应用最为广泛的退化过程模型，能够描述多种典型产品的退化失效过程，如机械零件的疲劳、腐蚀和裂纹扩展等，在保证退化过程的单调性的同时且易于编制程序进行分析计算。

如果具有独立增量的连续时间随机过程{X(t),t≥0}初始值为0，且在任意时刻服从均值为0，方差为t的正态分布则称为标准Wiener过程，即：

(1)X(0)=0

(2) 对于任意两个不重叠的时间段[t1,t2]和[t3,t4]，增量X(t2)-X(t1)与X(t4)-X(t3)相互独立。

(3)X(t)～N(0,t)

相应的，带有漂移的Wiener过程可以表示为：

X(t)=at+bβ(t)

(11)

其中，a是漂移系数，b是扩散系数，{β(t),t≥0}是标准的Wiener过程。与标准Wiener过程围绕0点做随机运动不同，带有漂移的Wiener过程增加了趋势项at，可以用来描述产品性能退化的单调过程。因此，如果用X(t)表示t时刻的强度退化量，则在t时刻的均值和方差为：

E[X(t)]=at

(12)

Var[X(t)]=b2t

(13)

且由于时刻t～t+Δt之间的增量ΔX服从正态分布，增量ΔX可能大于、等于或小于0，因此一元Wiener过程不是严格的单调退化过程，但是当漂移参数a和扩散参数b相比较大时，从总体趋势上看退化过程仍然可以近似看作单调过程[16]。

3 可靠性灵敏度分析

可靠性灵敏度定义为失效概率Pf对基本随机变量的分布参数的偏导数，它定量地反映了随机变量的分布参数对于结构失效概率的影响程度，根据可靠度R或者失效概率Pf的计算公式以及可靠性指标β与随机变X量的函数关系，结构失效概率对参数均值和方差的灵敏度计算公式可以表示为：

(14)

(15)

(16)

可靠度指标对基本随机向量的均值与标准差的偏导数为：

(17)

(18)

于是，随机向量对失效概率Pf可靠性灵敏度的最终解为：

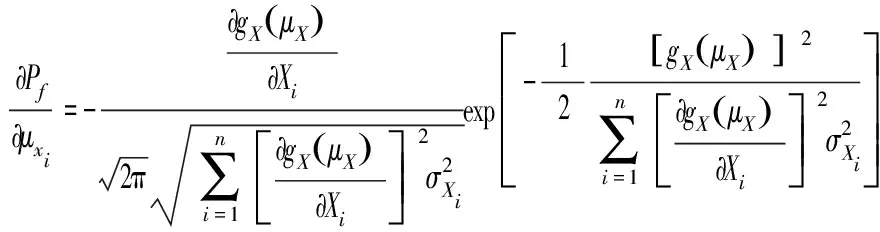
(19)

(20)

相对应的，根据可靠度与失效概率的关系，随机向量对可靠性灵敏度可以表示为：

(21)

(22)

4 算例

以螺栓为具体算例，螺栓参数在表1中给出，带漂移的一元Wiener过程的参数为a=0.003，b=0.04，螺栓的可靠性模型为应力强度干涉模型，分别用r随机变量函数表示螺栓的许用剪切强度和工作应力，其工作应力表示为：

(23)

式中，P为螺栓承受的剪切载荷；d为螺栓的截面直径；N为剪切面数。

其强度退化量表示为：X(t)=at+bβ(t)

(24)

式中，a为漂移参数；b为扩散参数。

其状态函数为：

g(X)=r-σ

(25)

式中，r为螺栓许用剪切强度，基本随机变量为X=(r,P,d)T。

表1 螺栓参数

使用一次二阶矩方法对此模型进行可靠性及可靠性灵敏度分析计算。

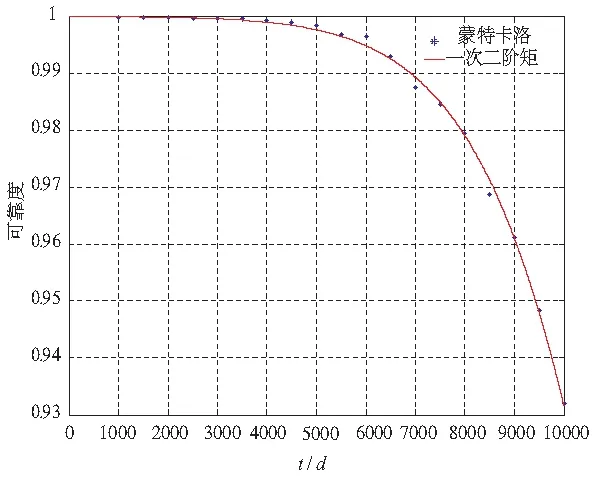
图1 强度退化得螺栓可靠度曲线

可靠度计算结果如图1所示，从图中可以看出，与Monte Carlo方法计算的螺栓强度退化结果相比，两种算法得到的计算结果非常接近，一次二阶矩方法具有很高的计算精度，用此方法计算强度退化的可靠度结果可以接受。

图2 强度退化得螺栓方差灵敏度曲线

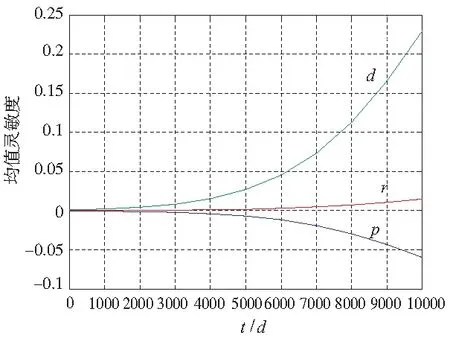
图3 强度退化得螺栓均值灵敏度曲线

图2、图3分别为螺栓可靠度对其承受的剪切载荷p，螺栓截面直径d、螺栓的许用剪切强度r的均值和方差的灵敏度曲线，从图中可以看出，基于Wiener退化过程螺栓的可靠度具有以下特点：①可靠度对螺栓直径的均值最为敏感，其次是螺栓所承受的剪切载荷的均值，并且为负值，最不敏感的是螺栓初始许用强度的均值；②可靠度对所有参数的方差灵敏度都是负值，影响水平顺序依次是螺栓承受的剪切载荷，螺栓的直径以及螺栓的许用强度；③灵敏度的绝对值都是随时间变化逐渐增大；④若想提高螺栓的可靠度，主要是增大螺栓直径的均值，并且减小螺栓直径的方差，或者减小螺栓承受的剪切载荷的均值。

5 结论

本文通过使用带漂移参数的Wiener过程描述强度退化过程，在传统的应力-强度模型中加入随机过程的数学方法，可以对由于材料内部结构的变化导致的机械零件失效进行数学定量描述。使用Wiener过程能够描述个体差异，并且一般不会给模型参数的估计带来过多的困难。以螺栓为实例演示所述方法，可以推广到更多的机械部件和机械系统中，本文采用的可靠性和可靠性灵敏度计算方法，能很好的在设计初期预测产品的使用寿命、强度退化情况，以及产品设计参数对产品整体可靠性及强度退化的影响，以利于发现产品设计参数的潜在缺陷。

(1)本文以应力强度干涉模型为基础，采用Wiener随机过程描述结构的强度退化过程，使用一次二阶矩方法计算了机械零部件的时变可靠性并进行了可靠性灵敏度分析。并将结果与蒙特卡洛模拟方法进行对比，显示其准确性。

(2)以螺栓为例，假设螺栓强度退化服从Wiener随机过程，进行了时变可靠性计算及灵敏度分析。从灵敏度分析结果中可以看出在螺栓的可靠性设计中，可以通过增大螺栓截面直径、提高许用强度或者是减小螺栓承受的剪切载荷来实现提高螺栓的可靠性。灵敏度分析结果为螺栓的设计提供了理论依据。