基于“翻转课堂”的“概率论与数理统计”课程教学研究

王婧

摘 要 基于翻转课堂教学法的研究，结合“概率论与数理统计”课程教学实践，通过对现有的教学模式加入提问题-讨论-解答的环节，提高学生自主学习、分析问题和解决问题的能力，并且以随机变量函数的分布教学为例，说明翻转课堂在教学中的应用。

关键词 翻转课堂 概率统计 教学研究

中图分类号：G424 文献标识码：A DOI：10.16400/j.cnki.kjdkz.2018.04.060

Abstract Based on the research of flipped classroom teaching methods， combining with the course teaching practicing about the theory of probability and mathematical statistics， through to the existing teaching mode to join questions-discussion-answer link， improving the students' autonomous learning， problem analysis and problem solving skills， and take an example for the distribution of random variable function teaching which is illustrating the application of reverse classroom in the teaching.

Keywords flipped classroom； probability and statistics； teaching and research

0 引言

随着现代科学技术的突飞猛进，概率论与数理统計越来越受到人们的重视与青睐，如生物统计，数理经济等学科都离不开它，概率论与数理统计是理工科各专业大学生的必修课之一，它的概念较抽象，知识点较多，实际应用广泛，但是学生普遍反映不好理解，而现有的教学，由于课堂时间有限，还是以“老师讲，学生听”为主要教学形式，大部分学生都处于被动学习的地位，久而久之，自然也就失去学习兴趣，积极主动性不高。基于这门课程的重要性，需要引入新的教学方法，激发学生的学习兴趣，调动学生的主观能动性。

翻转课堂由“Flipped Classroom”英译而来，是通过重新调整学生课堂内外的时间，将学习的决定权由教师转移到学生的一种新的教学模式。在这种教学模式下，教师可以不占用有限的课堂时间来讲解内容，学生可以在课前和课后自主学习，借助互联网技术观看教学视频，还能在网络上与同学讨论，拓展了学生学习知识的途径和方法。为学生课前的学习创造物质条件，引导学生利用互联网资源成为关键，因此，随着教师角色的变化，教师如何引导学生将课前学习的知识点在课堂上进行表达成为关键，引导学生提出问题，进而分析讨论，最后引导学生自主解决问题。此前已有关于此类问题的讨论，如参考文献[1]-[8]，本文在此基础上，进行适当拓展，将翻转课堂加入到“提出问题——讨论问题——解决问题”的模式中。

1 翻转课堂教学法的特点及其实施过程

1.1 翻转课堂的特点

翻转课堂实现了教师从注重知识的讲授到关注学生的发展的转变，尤其是教学视频的引入，传递给学生关键问题，引导学生自我思考，自我寻求知识，提高学生发现问题、解决问题的能力。与传统教学的区别是：学习时间更灵活自由，学生可以随时观看老师制作的视频和课件，并可反复观看，以巩固所学知识；教师不再是一味地讲解，学生不再一味地听讲记笔记；学生观看视频后，有相应的小测验，并对自己所学知识有所反馈；课堂上，教师更注重的是问题的讨论，学生自主发言，发现问题，解决问题。

1.2 翻转课堂教学步骤

（1）课前准备，教师在课前录制视频，将本节课的知识点、重点问题、难点问题均列举出来，讲解清楚，学生通过观看视频，了解本节课的知识点，把疑难问题记录下来，以便在课堂上讨论。

（2）课堂讨论、答疑，学生首先通过视频将疑难问题提出来，大家共同讨论，最终由教师答疑解惑并加以总结。将课堂上一味的讲授转换为针对性的辅导，提高学生的自主学习能力。将课堂教学转变为“提出问题——讨论问题——解决问题”的新模式。

（3）课后测评，通过对所学知识进行小测试，既可以测评学生对于知识的掌握程度，又可以对视频讲解的不足加以优化，更新教学视频，使得学生可以“温故而知新”。

2 翻转课堂教学实例

通过对翻转课堂教学法的学习，将其引入“概率论与数理统计”课程教学中，为此选取了随机变量函数的分布教学为例：

例：设随机变量X具有概率密度，求 的概率密度。

（1）课前准备阶段，通过教师制作微视频：包括基本概念，基本知识点，重点，难点的讲解，使学生能够很好地掌握，理解本节知识。

回顾离散随机变量分布→离散随机变量函数的分布；（此分布是比较容易理解）

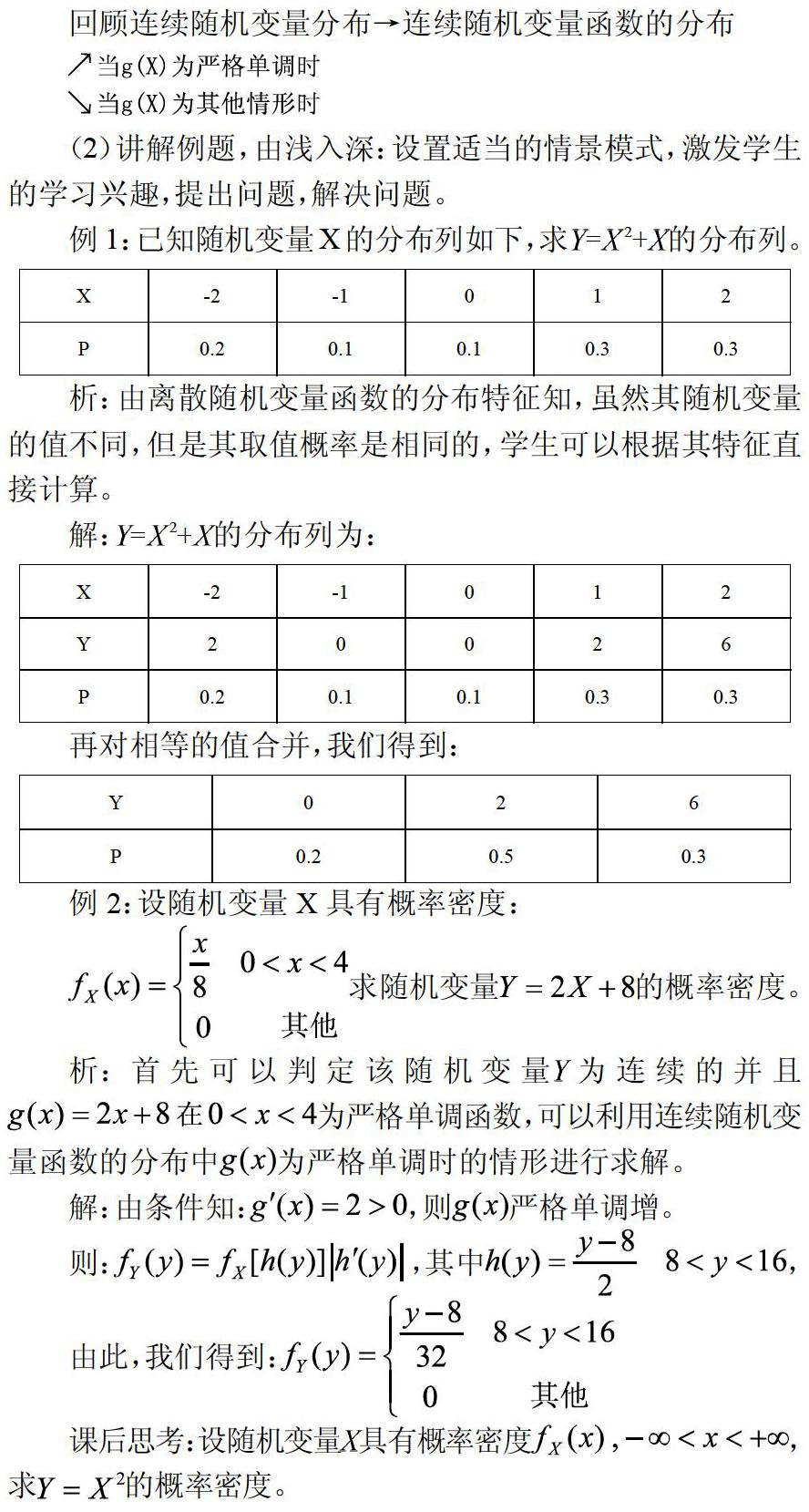
回顾连续随机变量分布→连续随机变量函数的分布

由此，我们得到：

课后思考：设随机变量具有概率密度，求的概率密度。

（3）总结，学生看完例题1、2的讲解可以自由讨论，查找疑惑，课上进行解答，同时留有思考题，让学生自由发挥，开放思想，进行解答，提高课堂利用效率。

3 结语

通过翻转课堂在“概率论与数理统计”教学中的实践应用，我们发现，学生在学习中的主动作用体现出来，学生学会学习，学会思考。不仅提高了教师的教学效果，也激发了学生的主观能动性。因此，翻转课堂可以解决现有的教学问题，但在今后的教学工作中还需要不断努力，对翻转课堂加以优化。

参考文献

[1] 宁桂英，莫京兰，黄秋和.翻转课堂在《概率论与数理统计》教学中的应用研究[J].教育教学论坛，2017（36）：167-168.

[2] 杨洪，丁艳清，朱桂英.“翻转课堂”教学法在《概率论与数理统计》课程中的实践[C].深化教学改革·提升高等教育质量，2015.

[3] 刘静，刘宏伟，李斌.基于MOOC的"概率论与数理统计"翻转课堂研究[J].工业和信息化教育， 2017（1）：43-45.

[4] 张玲玲，黄建华，黄立宏.基于微课的概率论与数理统计翻转课堂教学模式实践[J].高教学刊， 2017（8）：61-62.

[5] 廖楚越.概率论与数理统计的翻转教学[J].课程教育研究，2016（8）：145-145.

[6] 武萌，尹亮亮，刘晓霞.基于教学翻转模式的概率论与数理统计教学改革探索[J].科学大众：科学教育，2015（11）：148-149.

[7] 王子龙，高歌.古典概型的翻转课堂设计[J].知识文库，2017（1）.

[8] 赵攀.概率论与数理统计教学改革探讨[J].九江学院学报（自然科学版），2012.28（3）：121-122.