基于多线性强化材料模型的轧机轴承有限元分析
李万嘉,王景华,邓四二,3,4,张文虎
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.洛阳轴承研究所有限公司,河南 洛阳 471039;3. 西北工业大学 机电学院,西安 710072;4. 辽宁重大装备制造协同创新中心,辽宁 大连 116024)
四列圆柱滚子轴承常用于轧钢机架的轧辊颈、滚筒和轧压机中,常工作在超高载荷的环境中并伴随着频繁冲击,会出现轴承接触应力过大导致的轴承早期失效。通常采用滚子素线修形和加工合适空心度的方法降低滚动轴承接触应力,并采用表面处理方法提高滚道表面硬度从而改善轴承的抗冲击能力[1]。故有必要分析滚子素线修形、滚子空心度及滚子和滚道硬化层深度对滚子与滚道接触应力及塑性应变的影响。
国内外学者对轴承接触应力做了大量研究,文献[2]分析得出轴承滚道硬化层深度不够会导致轴承过早失效;文献[3]分析了滚动轴承滚道表面硬化层深度与其承载能力的关系;文献[4]建立了非线性随动强化模型,并由试验及有限元法证明了该模型可以准确预测材料在百万次级循环载荷作用下不同硬化层中的塑性应变;文献[5-9]分析了材料缺陷引起局部应力及应变过高的机理,并分析了载荷、滚子修形、缺陷位置及缺陷尺寸对疲劳特性的影响;文献[10]建立了航空发动机用滚动轴承的有限元分析模型,分析了载荷对轴承接触应力、接触角及变形的影响;文献[11]建立了球轴承有限元模型,分析了径向载荷、表面曳引力以及沟曲率半径对裂纹扩展的影响;文献[12]通过建立滚动轴承的混合模型,分析了存在表面缺陷时滚动轴承滚道的接触应力及接触角等;文献[13]分析了四列圆柱滚子轴承的接触应力、变形及径向刚度,得到了该轴承刚度随径向载荷的变化规律;文献[14]通过选用双线性等向强化模型和双线性随动强化模型,分析了不同变形本构关系材料模型的低速轴承在2种工况下的应力分布状况;文献[15]给出了4种不同圆柱滚子修形素线时沿滚子素线方向的应力分布;文献[16]采用工程对数凸型对滚子素线参数进行优选设计,避免了边缘效应,使滚子和内圈的应力下降;文献[17]建立了滚子受力平衡方程,分析了滚子空心度、外载荷、轴承转速及滚子个数对刚度的影响;文献[18]基于Hertz接触理论对空心滚子轴承进行了有限元分析,并对轴承空心度进行了优化设计。
上述研究的材料模型大部分采用线弹性材料,并未考虑轴承的表面硬化及材料塑性的影响。鉴于此,基于ANSYS建立大型四列圆柱滚子轴承有限元分析模型,选用多线性强化材料塑性应变模型,分析硬化层深度、滚子素线修形及滚子空心度对轴承最大接触应力及最大塑性应变的影响。
1 有限元模型
以某轧机用四列空心圆柱滚子轴承为例分析,轴承结构如图1所示,其主要结构参数见表1。
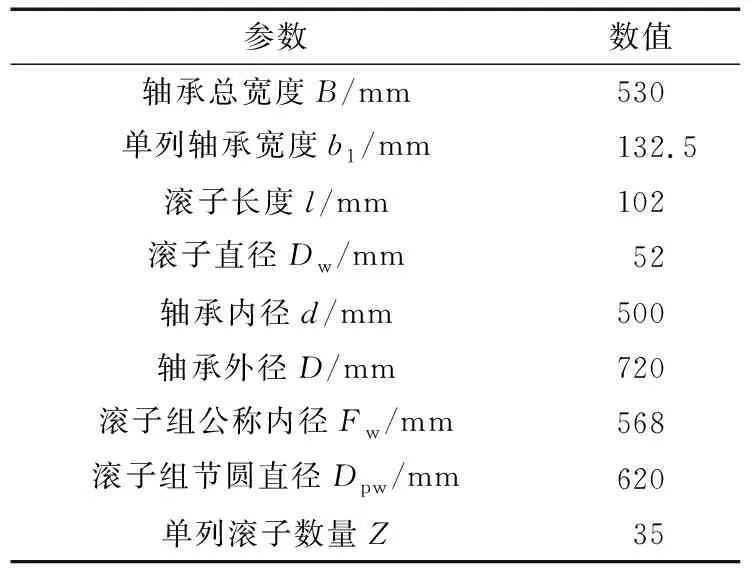
表1 主要结构参数Tab.1 Main structural parameters
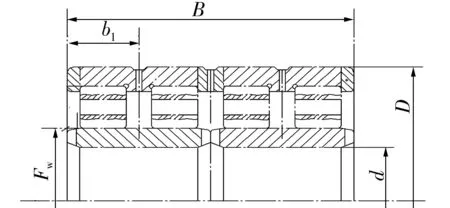
图1 四列圆柱滚子轴承Fig.1 Four row cylindrical roller bearing
1.1 模型建立
该轴承尺寸较大,为提高计算效率,在仿真分析时仅取受载最大的滚子与内、外圈滚道接触部分的一半建模,其模型如图2所示。为使网格划分合理,需要对模型进行切分,不同切分方法网格划分不同,从而导致相同载荷下分析结果略有不同。在此将内、外圈滚道以及滚子由表面到内部每1 mm切分一层,共10层,如图3所示。该切分方法可分别定义每一层的材料,在分析硬化层深度的影响时不需要再根据层深重新切分,减小了由模型切分不同而造成的误差。

图2 有限元模型Fig.2 Finite element model

图3 切分模型Fig.3 Segmentation model
1.2 材料模型
该轴承材料模型有2类:1)硬化层材料模型;2)芯层材料模型(除硬化层之外的材料)。材料参数见表2,E为弹性模量,σy为材料屈服极限,K为材料强度极限,n为应变硬化系数,ν为泊松比。

表2 材料模型参数Tab.2 Parameters for material model


图4 应力-应变曲线Fig.4 Stress-strain curves
1.3 网格划分与载荷约束
采用六面体网格进行网格划分,对接触部位网格进行局部细化,整体网格划分如图5a所示,局部细化网格如图5b所示,单元数为107 412,节点数482 387。固定外圈外表面,在截面处施加对称约束,在内圈内表面施加径向载荷。

图5 网格划分Fig.5 Meshing
2 仿真分析
2.1 滚子修形方式对滚子最大接触应力的影响
滚子和滚道硬化层深度为0,空心滚子内径Dwi为13.5 mm,空心度为26%。滚子素线为2种形状,三段修形如图6a所示,对数修形如图6b所示。
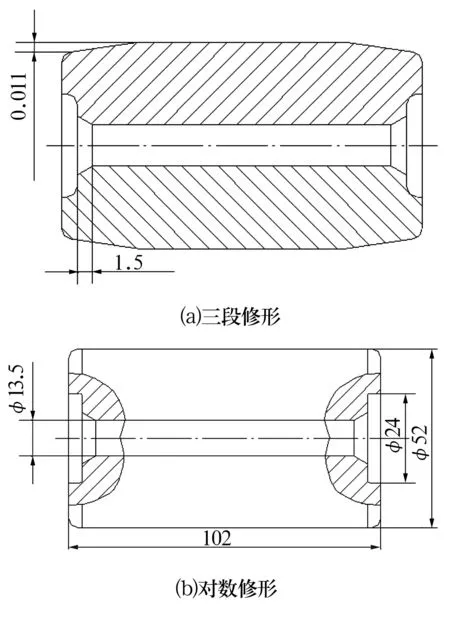
图6 不同滚子素线修形Fig.6 Different generatrix profiling of roller
对数修形素线方程为
(1)
凸度近似值为
式中:x为滚子长度方向的坐标,在滚子中心处x=0;Q为滚子与滚道之间的法向接触载荷;b为接触半宽;K0=2.81×10-6mm2/N。
单个滚子所承受的极限载荷为400 kN,极限载荷下2种素线修形下的滚子接触应力如图7所示。由图可知:三段修形滚子最大接触应力达到了4 822.6 MPa,远远大于材料的屈服极限;对数修形滚子最大接触应力明显较小,最大值为4 195.2 MPa,最大接触应力降低了13%。下述分析均以对数修形滚子作为研究对象。
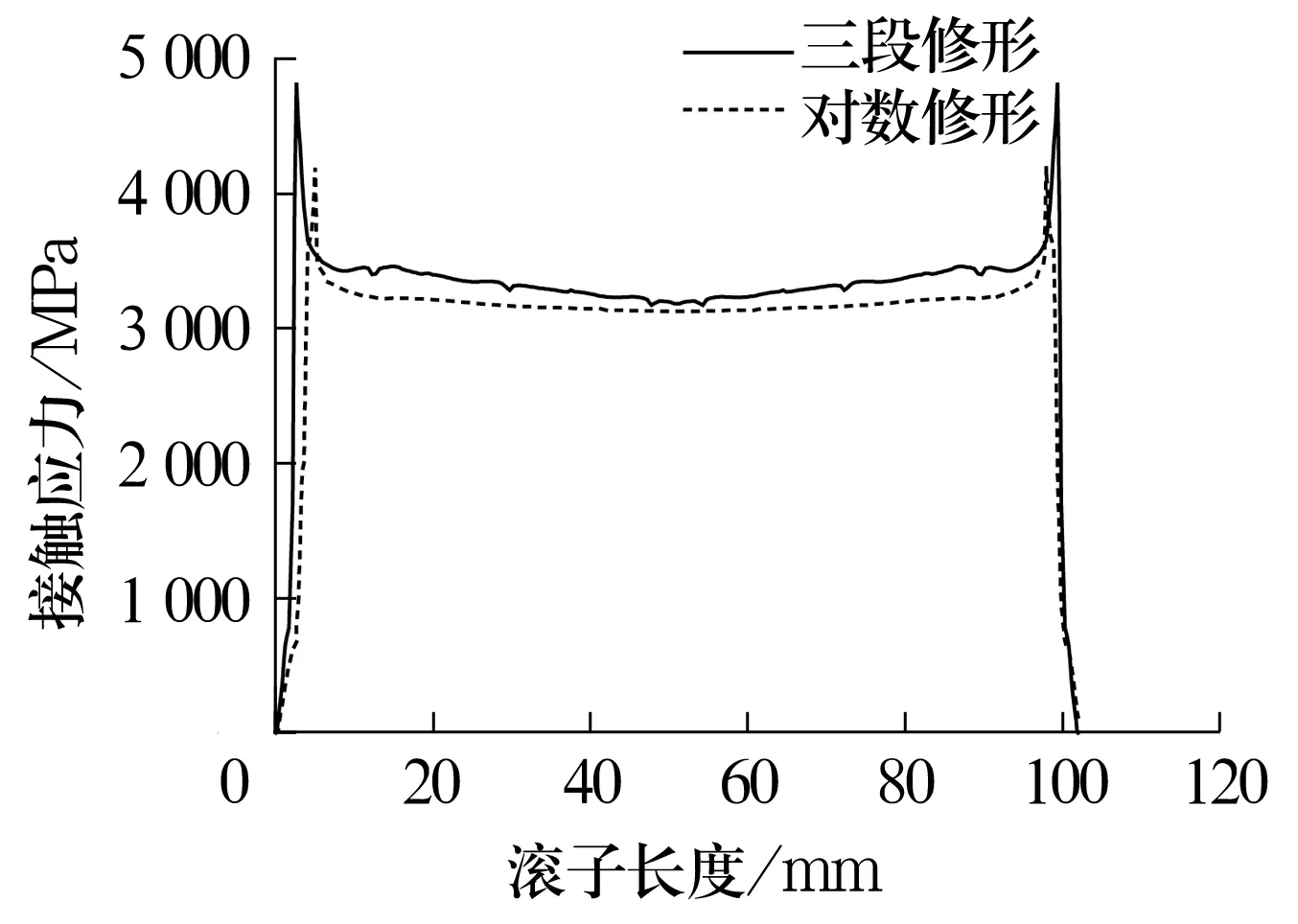
图7 极限载荷下2种滚子修形的最大接触应力Fig.7 Maximum contact stress of two profiling methods for roller under limit load
2.2 内滚道硬化层深度对最大接触应力和最大塑性应变的影响
根据接触关系可知,滚子与内滚道的接触应力大于滚子与外滚道的接触应力,因此仅分析内滚道硬化层深度对滚子与滚道最大接触应力和最大塑性应变的影响。在滚子硬化层为0 mm,空心度为26%,且为对数修形时,极限载荷作用下内滚道硬化层为0~10 mm时滚子与内滚道的最大接触应力和最大塑性应变分别如图8和图9所示。从图中可以看出:滚子与内滚道的最大接触应力随内滚道硬化层深度增加先快速增加后缓慢增加,在硬化层达到4 mm时最大接触应力趋于平稳;随内滚道硬化层深度增加,内滚道最大塑性应变先快速减小,后缓慢减小,在硬化层达到7 mm后内滚道最大塑性应变趋于平稳;滚子最大塑性应变先快速增大后缓慢增大,在硬化层达到7 mm时最大塑性应变趋于平稳。这是由于滚道硬化层深度不断增加,滚道的硬度也逐渐变大,而滚子的硬度没有改变,因此同样的载荷下,滚道的塑性应变降低而滚子的塑性应变变大,同时使得滚子及滚道的最大接触应力增大;载荷不变的情况下,当滚道硬化层达到一定深度后,滚道的塑性应变发生在滚道硬化层中,此时继续增加硬化层深度,滚子及滚道的塑性应变以及最大接触应力都保持不变。综合考虑,滚道的硬化层深度为7 mm时最为合适。
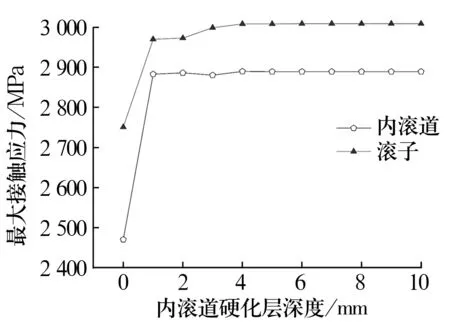
图8 最大接触应力随内滚道硬化层深度的变化曲线Fig.8 Variation curve of maximum contact stress with hardened layer depth of inner raceway
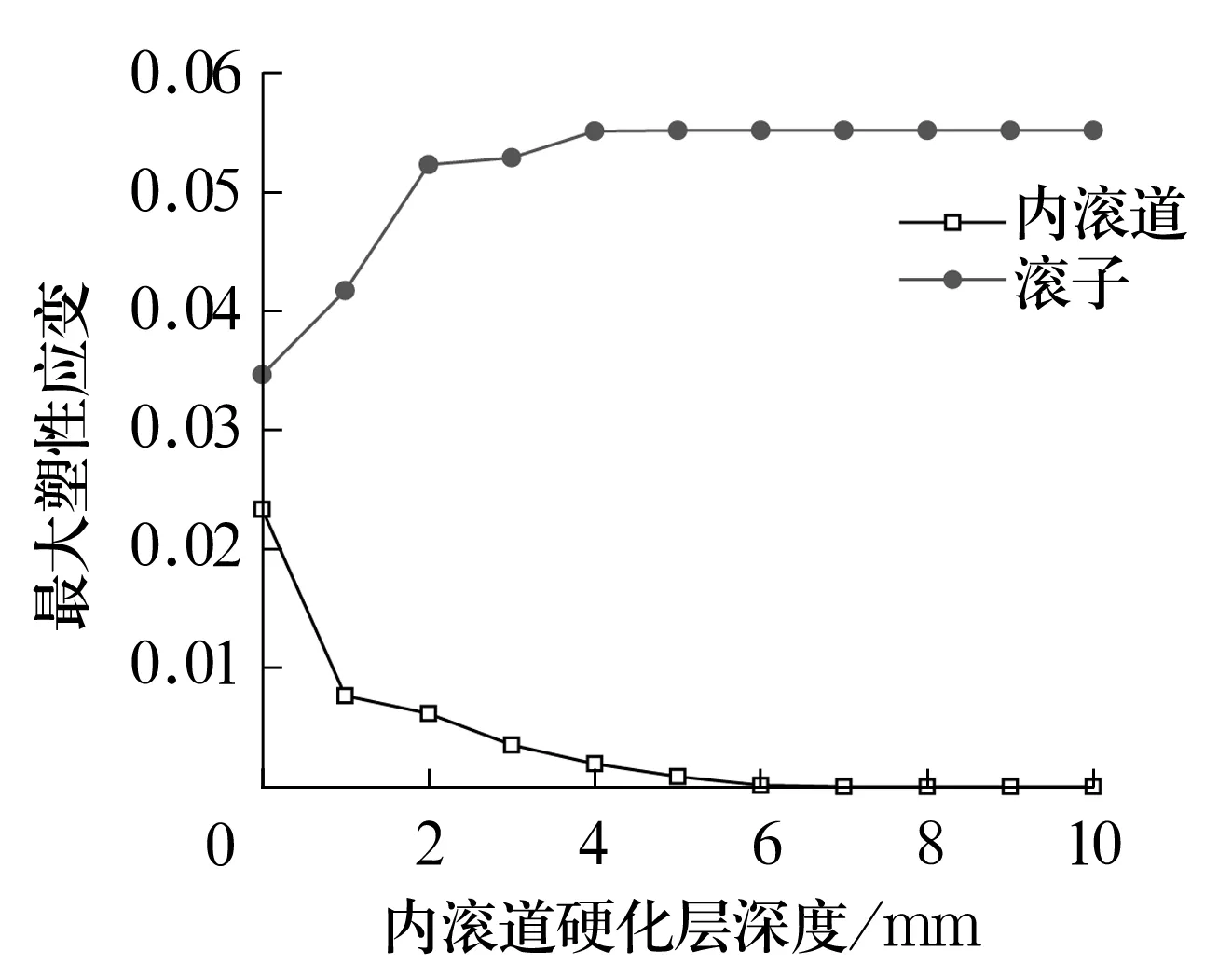
图9 最大塑性应变随内滚道硬化层深度的变化曲线Fig.9 Variation curve of maximum plastic strain with hardened layer depth of inner raceway
2.3 滚子硬化层深度对最大接触应力和最大塑性应变的影响
在内滚道硬化层为7 mm,滚子空心度为26%,且为对数修形时,极限载荷作用下滚子硬化层为0~10 mm时滚子与内滚道的最大接触应力和最大塑性应变分别如图10和图11所示。从图中可以看出:滚子和内滚道的最大接触应力随滚子硬化层深度增加先快速增加而后缓慢增加,在硬化层达到3 mm时最大接触应力趋于平稳;随滚子硬化层深度增加,内滚道最大塑性应变缓慢增大,滚子硬化层为3 mm时内滚道的最大塑性应变趋于平稳;滚子最大塑性应变先快速减小而后缓慢减小,同样在滚子硬化层达到3 mm时最大塑性应变趋于平稳。这是由于随着滚子硬化层深度的增加,滚子硬度逐渐变大,而此时内滚道硬度小于滚子,故在同一载荷下滚子塑性应变减小而内滚道塑性应变增大,同时使滚子、内滚道的最大接触应力增大;在载荷不变的情况下,当滚子硬化层达到一定深度后,滚子的塑性应变发生在滚子硬化层中,此时若继续增加硬化层深度,滚子和内滚道的塑性应变及最大接触应力均保持不变。当滚子硬化层深度为3 mm时,能满足抗冲击能力要求,继续增大硬化层深度,其加工成本较高,故滚子硬化层深度3 mm最佳。

图10 最大接触应力随滚子硬化层深度的变化曲线Fig.10 Variation curve of maximum contact stress with hardened layer depth of roller
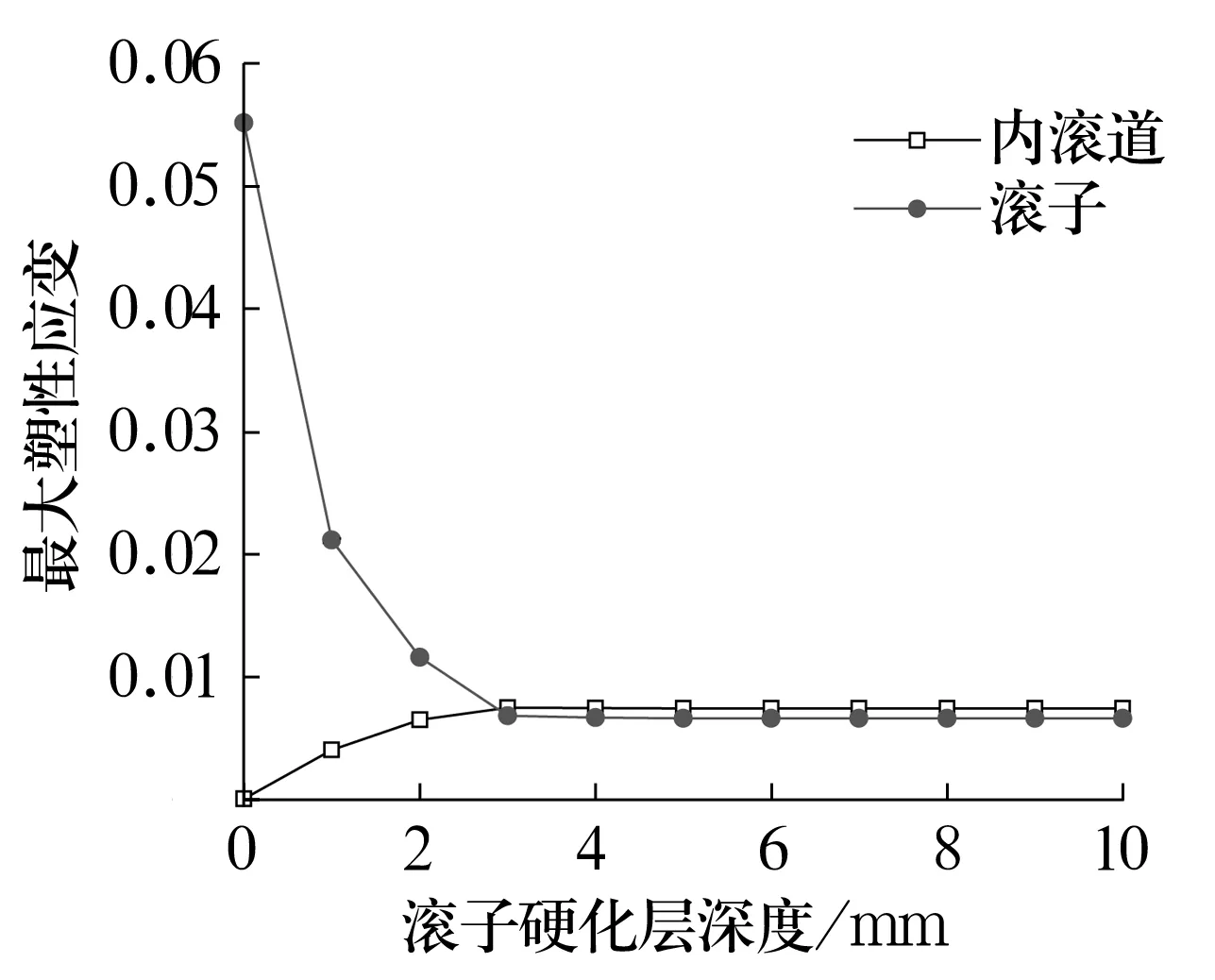
图11 最大塑性应变随滚子硬化层深度的变化曲线Fig.11 Variation curve of maximum plastic strain with hardened layer depth of roller
2.4 滚子空心度对滚子最大等效应力和最大接触应力的影响
在滚子和滚道硬化层深为0 mm,且滚子为对数修形时,分析在极限载荷下滚子空心度分别为10%,20%,30%,40%,50%,60%,70%,80%时滚子的最大接触应力和最大等效应力,结果如图12所示。滚子空心度分别为10%,30%,50%,70%时滚子的等效应力云图如图13所示。
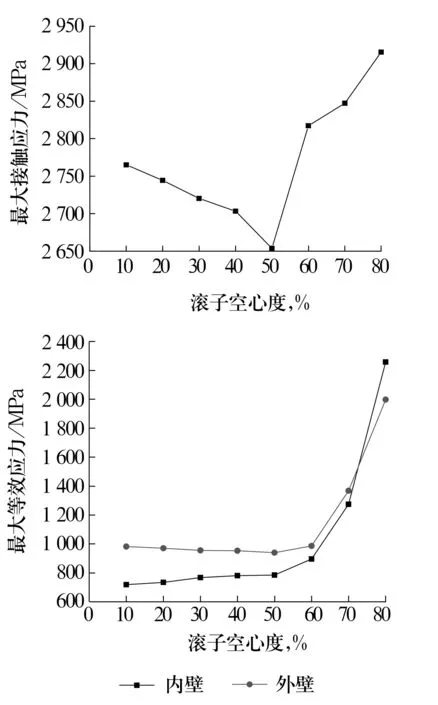
图12 空心度对滚子最大接触应力和最大等效应力的影响Fig.12 Influences of hollowness on maximum contact stress and maximum equivalent stress of roller

图13 不同空心度下滚子的等效应力云图Fig.13 Equivalent stress nephogram of rollers with different hollowness
从图中可以看出:滚子的最大等效应力随空心度增大,逐渐由接触位置转移到滚子内壁位置;当空心度小于50%时,滚子内壁最大等效应力随空心度的增大而缓慢增大,滚子外壁最大等效应力随空心度增大而缓慢减小;当空心度大于50%时,滚子内(外)壁最大等效应力随着空心度的增大而迅速增大,滚子内壁的最大等效应力逐渐大于滚子外壁的最大等效应力。当空心度小于50%时,滚子的最大接触应力随空心度增大而不断减小;当空心度大于50%时,滚子最大接触应力随空心度增大而不断增大。这是由于对数修形的滚子随空心度增大滚子与内滚道的接触半宽增大,最大接触应力减小,此时的最大接触应力发生在滚子两端;然而随空心度进一步增大,滚子两端的最大接触应力逐渐减小,即所谓的边缘效应逐渐降低,当空心度大于50%时,滚子最大接触应力由两端转移到了滚子中心部位,接触应力会逐渐升高。故最佳空心度为50%。
3 结论
建立了大型四列圆柱滚子轴承有限元模型,选用多线性强化材料塑性应变模型,通过仿真分析得出如下结论:
1)采用滚子素线对数修形,滚子接触应力降低了13%。
2)随内滚道硬化层深度增加,内滚道最大塑性应变先快速减小而后缓慢减小,在硬化层达到7 mm时,滚道最大塑性应变趋于平稳;滚子最大塑性应变先快速增大而后缓慢增大,同样在硬化层达到7 mm时,其最大塑性应变趋于平稳;而滚子和内滚道的最大接触应力先快速增加而后缓慢增加,在硬化层达到7 mm时,其最大接触应力趋于平稳。故内滚道硬化层深度最优为7 mm。
3)随滚子硬化层深度增加, 内滚道最大塑性应变先快速增大而后缓慢增大,在滚子硬化层达到3 mm时,内滚道最大塑性应变趋于平稳;滚子最大塑性应变先快速减小而后缓慢减小,同样在滚子硬化层达到3 mm时,其最大塑性应变趋于平稳;而滚子和内滚道的最大接触应力先快速增加而后缓慢增加,在硬化层达到3 mm时,其最大接触应力趋于平稳。故滚子硬化层深度最优为3 mm。
4)当空心度小于50%时,滚子内壁最大等效应力随空心度增大而增大,滚子外壁最大等效应力随着空心度增大而减小,滚子最大接触应力随空心度增大而减小;当空心度大于50%时,滚子内(外)壁最大等效应力随空心度增大而迅速增大,滚子最大等效应力由外壁逐渐转移到内壁,滚子最大接触应力随空心度增大而增大。故滚子最优空心度为50%。

