多瓦预载荷调整对核主泵轴系临界特性的影响
王祥,张帆,史朝阳,袁小阳
(西安交通大学 现代设计及转子轴承系统教育部重点实验室,西安 710049)
核主泵即核反应堆循环冷却剂泵,作为核岛内唯一高速转动的设备,其运行状况决定整个反应堆的安全性和稳定性[1]。核主泵等重大核电设备的转子系统均采用可倾瓦轴承支承。文献[2]对AP1000核主泵水润滑可倾瓦导轴承进行了性能仿真分析;文献[3]计算了CAP1400立式屏蔽电动机的上下径向轴承载荷、定转子环域水对转子动力学的影响;文献[4]通过模态分析和谐响应分析研究了陀螺效应对大型屏蔽电动机泵转子系统的临界转速和质量不平衡响应的影响;文献[5]通过Dyrobes软件计算了立式核主泵转子部件的一阶临界转速和振型。
我国在滑动轴承的流体动力润滑理论和转子动力学研究方面起步较晚,而国外学者已开展较多研究。文献[6]推导出了广义Reynolds方程;文献[7]基于可倾瓦块摆动频率和轴颈转动频率相同的假设,同时不考虑瓦块惯性、支点变形及支点摩擦力,提出了常规 8 系数的概念;文献[8-9]对可倾瓦轴承的常规 8 系数进行了计算和识别;文献[10-11]采用有限单元法对转子系统模态振型、固有频率、临界转速以及不平衡响应等问题进行了研究。
预载荷系数是可倾瓦轴承重要的结构设计参数,对其静动特性有重要影响,表征了轴承孔直径、轴颈直径、轴承间隙之间的关系[12]。文献[13]研究了可倾瓦轴承不同瓦块单独或组合调整预载荷对轴承动特性的影响规律,提出了改善可倾瓦轴承稳定性的“多瓦预载荷优化调整技术”,并以某五瓦可倾瓦轴承为例,详细介绍了瓦块预载荷计算和调整的方式;文献[14]分析了预载荷对屏蔽电动机主泵中上径向水润滑轴承静动特性的影响;文献[15]研究了预载荷调整在不稳定低频振动中的应用;文献[16]提出了一种混合型预载荷分布的可倾瓦轴承。对于高速轻载的透平机械,轴承的预载荷系数一般取0.2~0.5;对于载荷较重的汽轮发电机组,轴承的预载荷系数则常取0.5~0.7[17]。但对于核主泵转子系统,导轴承的预载荷系数是否越大越好,如何进行多瓦预载荷调整才能更好地控制轴系横向振动的临界特性,国内外学者的研究相对不足。
现针对高可靠性立式轴系的横向振动问题,以四瓦水润滑导轴承为研究对象,以多瓦预载荷调整为出发点,分析预载荷系数对导轴承静动特性的影响,同时采用模态分析方法计算2种典型的瞬态工况下轴系的一阶弯曲临界转速及模态振型,以期为核主泵水润滑导轴承的设计研究提供理论参考。
1 理论与模型
1.1 基本理论
直角坐标系下用于可倾瓦轴承性能分析的广义Reynolds方程为
(1)
式中:U为轴颈表面切向速度;V为轴颈表面径向速度;p为液膜压力;h为液膜厚度;r为轴颈半径;μ为润滑介质的动力黏度;Kx,Kz为流态系数。
在假设轴颈无偏斜的前提下,将瓦块的变形等效为一维梁变形,则热弹性变形方程可表示为
(2)
式中:R为瓦面的曲率半径;Δ为瓦面热弹径向变形量;φ为瓦上各点周向位置;M为瓦块弯矩;EI为抗弯刚度;q为瓦块轴向中分面上力分布;A为瓦块横截面面积;GA为抗剪刚度;α为瓦块热膨胀系数;ΔT为瓦面与瓦背温差;Hb为瓦块厚度。
固定参考系中用于转子动力学计算的通用方程为
(3)
1.2 模型建立
采用SOLIDWORKS软件建立某核主泵轴系的三维实体模型,如图1所示,轴系由转轴、上下导轴承、上下飞轮、叶轮组成。其中,转轴材质设置为不锈钢,飞轮材质设置为重金属钨合金,叶轮材质设置为钨。该轴系模型的整体质量约为19.55 t,极转动惯量约为2 577.46 kg·m2;单个飞轮的质量约为3.22 t,极转动惯量约为857.52 kg·m2。叶轮的质量约为2.95 t,极转动惯量约为383.52 kg·m2。上、下导轴承均为四瓦水润滑可倾瓦轴承,其主要结构运行参数相同,直径为416 mm,宽度为391 mm,瓦块数为4,额定转速约为1 500 r/min,支点系数约为0.5。
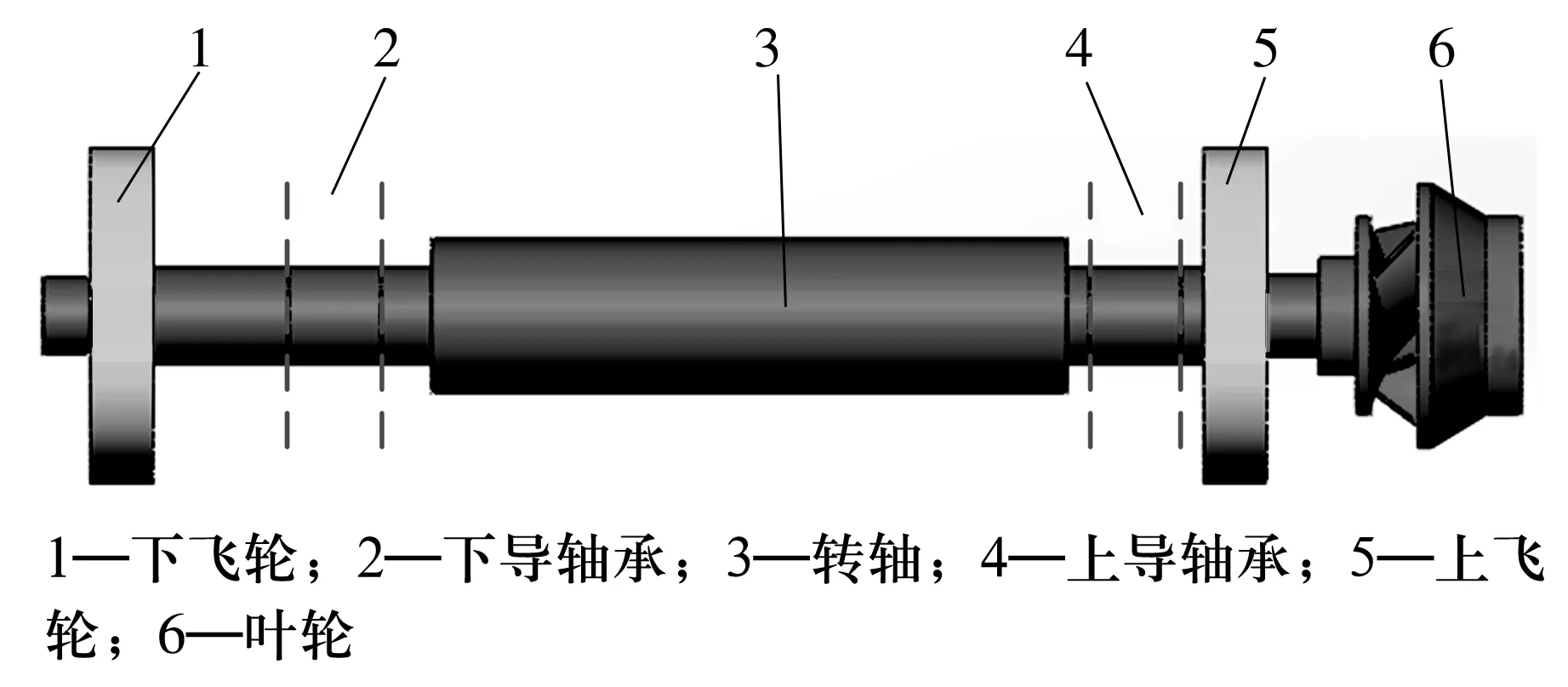
图1 核主泵轴系三维实体模型Fig.1 3D solid model of nuclear main pump shafting
在ANSYS中对轴系进行有限元建模和弹支模态分析。其中,转轴采用基于Timoshenko梁理论的BEAM188单元模拟,转轴的弹性模量为1.93×1011Pa,泊松比为0.31,密度为7 750 kg·m-3,上下导轴承采用二维弹簧阻尼单元COMBI214模拟,上下飞轮、叶轮采用结构质量单元MASS21模拟。
可倾瓦导轴承的载荷作用在其支点上时为瓦面承载,作用在支点间时为瓦间承载。对于所研究的立式转子系统,导轴承所承受的径向载荷的方向沿周向不断改变,同时上、下导轴承的支点位置周向错开45°,增加了轴系临界特性的求解难度。为此,选取2种典型的瞬态工况(表1)进行计算。

表1 2种典型的瞬态工况Tab.1 two typical transient operating conditions
工况1和工况2的区别是上、下导轴承的承载方式不同,例如:工况2下核主泵轴系的有限元模型如图2所示,图中F1,F2分别为上、下导轴承所受载荷。工况1和工况2虽不能完全代表轴系工作状态,但有重要的参考意义。

图2 工况2下核主泵轴系有限元模型Fig.2 Finite element model of nuclear main pump shafting under operating condition 2
对于四瓦可倾瓦导轴承(图3),单个可倾瓦块的预载荷系数δi的定义为
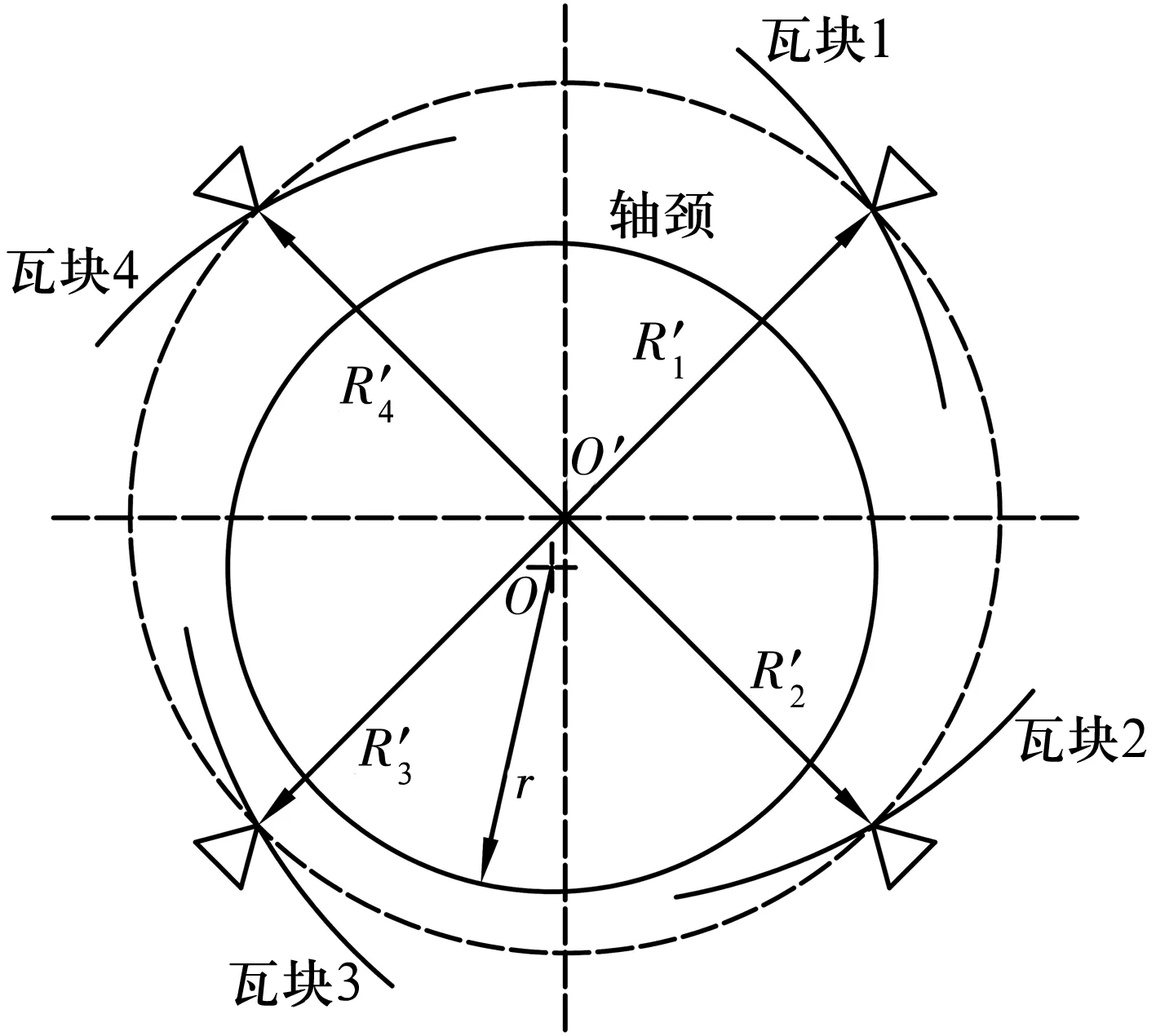
图3 四瓦可倾瓦导轴承结构简图Fig.3 Structure diagram of four-pad guide bearing
(4)
c=R-r,

2 多瓦预载荷调整对轴承静动特性的影响
由于均布四瓦可倾瓦导轴承支承的立式转子系统转动时的对称性,在进行多瓦预载荷调整时需保持每对轴承各瓦块的预载荷相等。针对额定转速、定值载荷条件下的上导和下导轴承,考虑瓦面承载和瓦间承载2种承载方式,通过同时改变4块可倾瓦块的预载荷系数,分析多瓦预载荷调整对轴承静动特性的影响。本计算案例中,上、下导轴承在不同承载方式下的载荷大小略有不同,导致其静动特性的变化趋势一致但具体数值略有差别。
在进行可倾瓦轴承性能求解时,采用有限差分法对Reynolds方程进行离散。程序语言为VB语言。模型为非等温模型并计入热弹变形效应,将瓦块简化为一维悬臂梁来分析热效应和弹性变形对轴承润滑性能的影响。可倾瓦轴承润滑性能包括静特性和动特性:静特性采用最小水膜厚度、平均温升、流量和功耗进行表征;动特性采用主刚度和主阻尼进行表征。
2.1 多瓦预载荷调整对轴承静特性的影响
导轴承的最小水膜厚度和平均温升随预载荷系数的变化曲线如图4所示(其中空心符号表示最小水膜厚度,实心符号表示平均温升),其流量和功耗随预载荷系数的变化曲线如图5所示(其中空心符号表示流量,实心符号表示功耗)。由图4可知:最小水膜厚度随预载荷系数的增大而减小,且减幅逐渐增大;平均温升随预载荷系数的增大而增大,且增幅逐渐增大。由图5可知:流量随预载荷系数的增大而减小,且减幅逐渐减小;功耗随预载荷系数的增大而增大,且增幅逐渐增大。造成上述结果的原因为:增大可倾瓦块的预载荷系数,则减小了其安装间隙和瓦块摆角(由图3可知),在二者的耦合作用下液膜厚度减小。可倾瓦轴承的最小液膜厚度应取所有瓦块中的最小值。由(1)式可知,液膜厚度减小,影响广义Reynolds方程的计算,进而影响液膜压力场、温度场的迭代求解,最终引起轴承静动特性的改变。
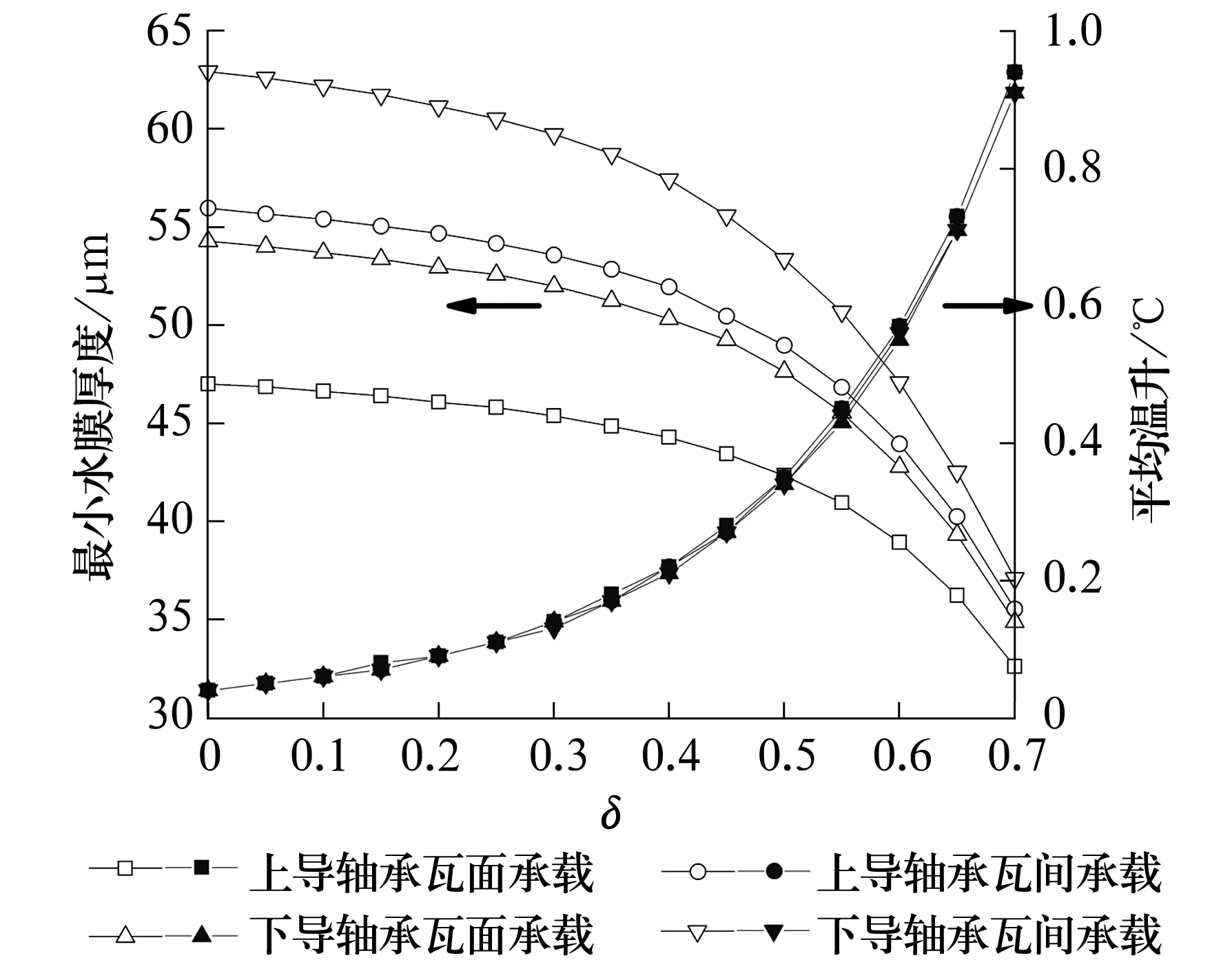
图4 最小水膜厚度和平均温升随预载荷系数的变化曲线Fig.4 Variation curve of minimal water film thickness and average temperature rise with preload factor
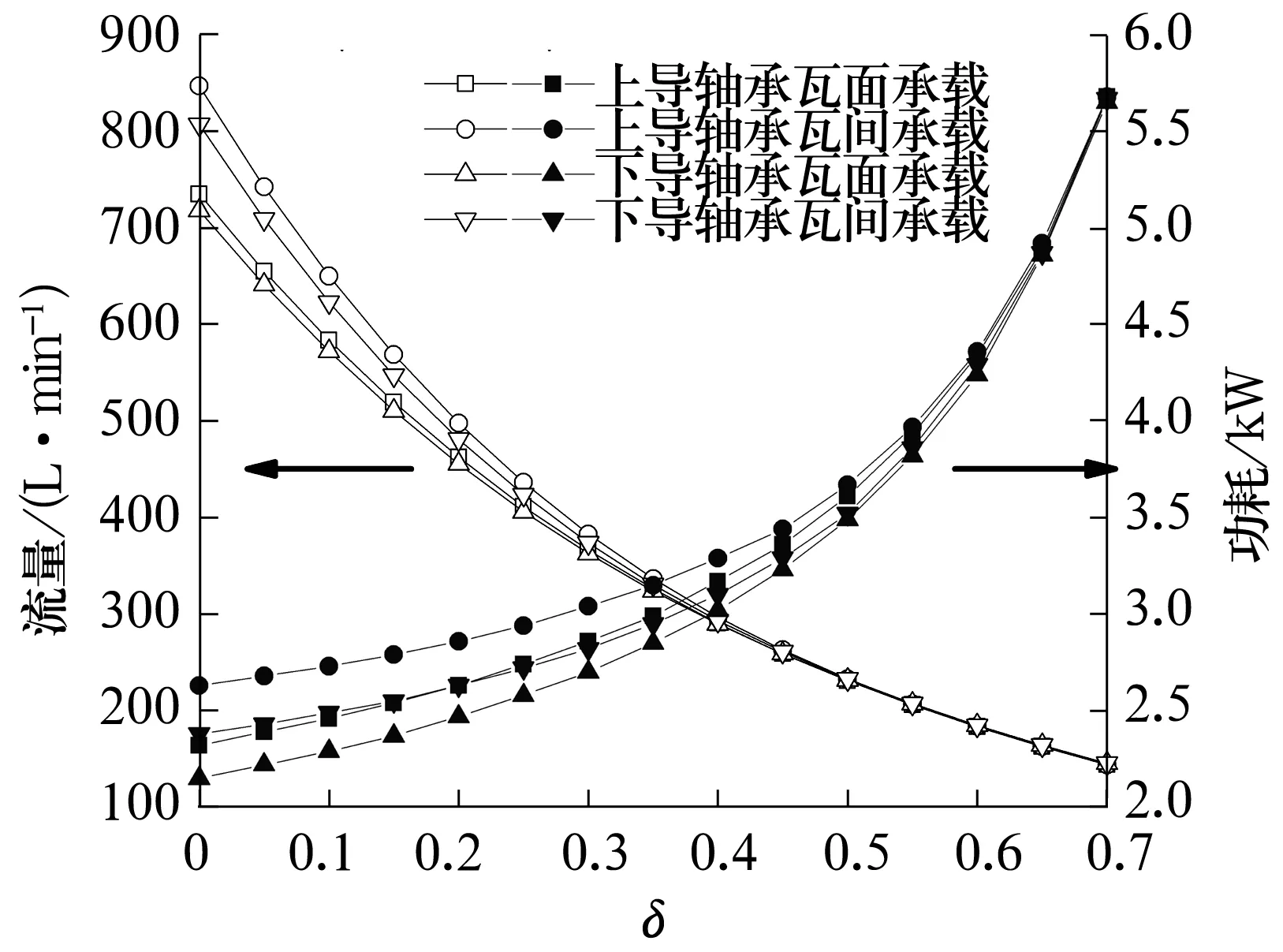
图5 流量和功耗随预载荷系数的变化曲线Fig.5 Variation curve of flow rate and power consuniption with preload factor
2.2 多瓦预载荷调整对轴承动特性的影响
上、下导轴承的主刚度和主阻尼随预载荷系数的变化曲线分别如图6和图7所示。由图可知:无论是采用瓦面承载还是瓦间承载,上、下导轴承的主刚度和主阻尼均随预载荷系数的增大而增大,且增幅逐渐增大。这是因为单个可倾瓦块的液膜力及刚度阻尼随预载荷系数的增大而增大,而可倾瓦轴承的刚度阻尼由各瓦块的刚度阻尼线性叠加得到。
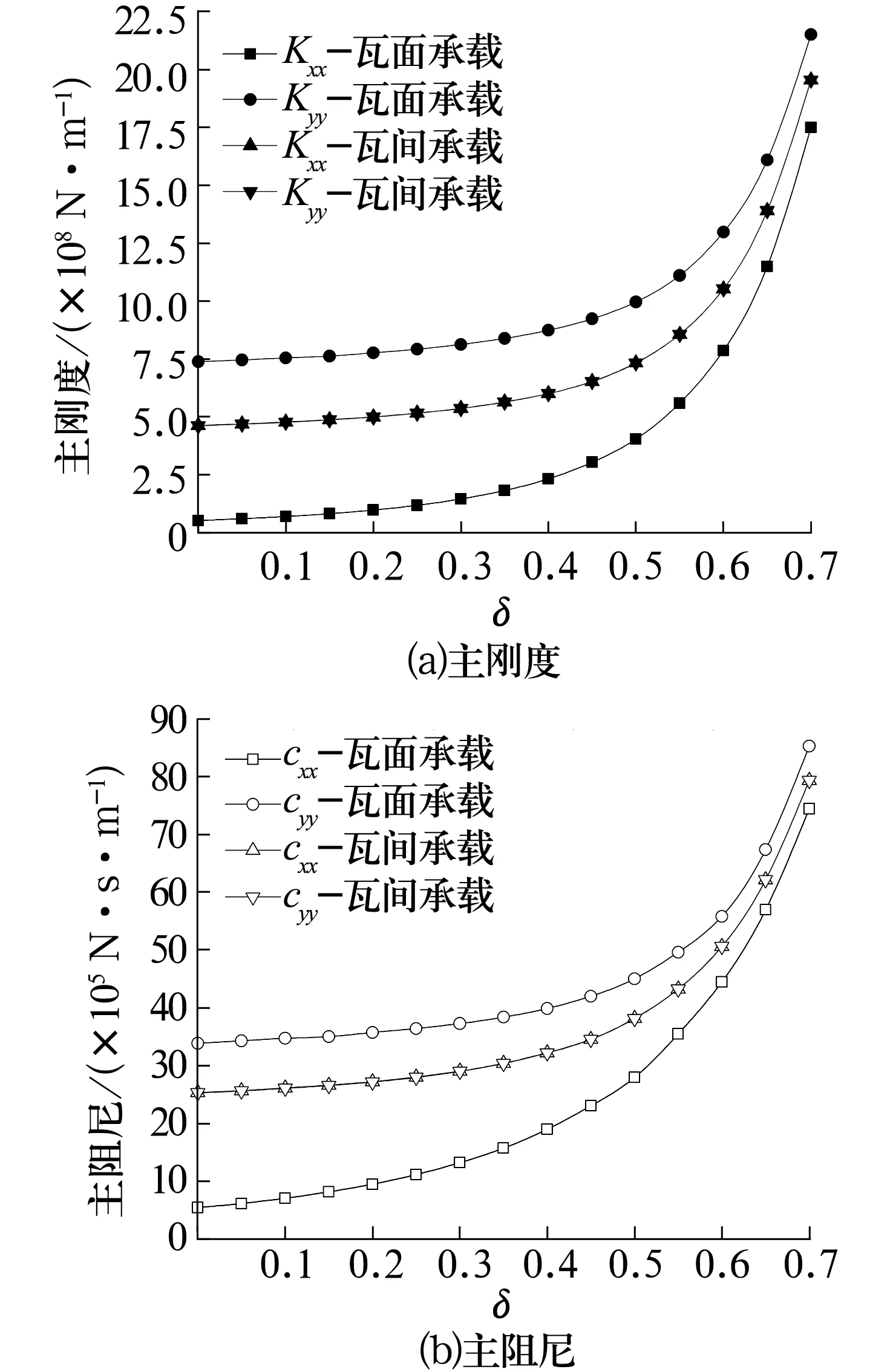
图6 上导轴承的主刚度和主阻尼随预载荷系数的变化曲线Fig.6 Variation curve of main stiffness and main damping of upper guide bearing with preload factor

图7 下导轴承的主刚度和主阻尼随预载荷系数的变化曲线Fig.7 Variation curve of main stiffness and main damping of lower guide bearing with preload factor
3 多瓦预载荷调整对临界特性的影响
3.1 多瓦预载荷调整对模态振型的影响
为了对比分析多瓦预载荷调整对轴系模态振型的影响,将该核主泵轴系三维实体模型由SOLIDWORKS软件导入到ANSYS Workbench中进行自由模态分析。采用自动网格划分(图8),单元总数为3 282,共有7 825个节点。

图8 网格划分Fig.8 Meshing
自由模态分析中前6阶模态的固有频率接近于0,可视为刚体模态,真正意义上的一阶模态是从自由模态分析中的第7阶模态开始的。在对核主泵轴系模型进行自由模态分析时不施加任何载荷,不考虑阻尼和陀螺效应,设置求解模态为11阶,求解后得到自由状态下的一阶弯曲振型如图9所示。
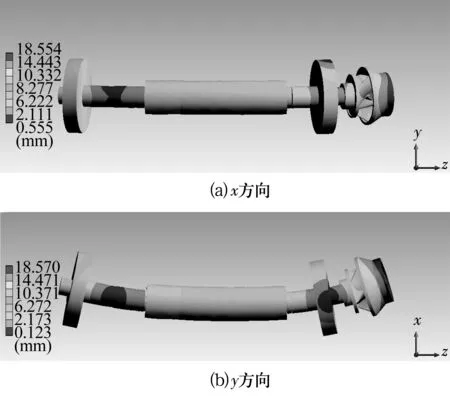
图9 自由状态下一阶弯曲振型Fig.9 First-order bending mode under free state
由图9可知,叶轮处的总变形量最大,设计和分析时需重视叶轮的强度。自由状态下核主泵轴系的一阶弯曲固有频率约为41.29 Hz。
针对额定转速、定值载荷、弹支状态下的核主泵轴系,以工况1为例,重点研究多瓦预载荷调整对模态振型的影响。在ANSYS中设置模态提取方法为QR阻尼法,同时考虑陀螺效应;对转轴上的所有节点施加轴向的位移约束和绕轴线的旋转约束,同时限制轴承节点处所有方向上的自由度。以不同预载荷系数下导轴承的常规8系数作为自变量,对核主泵轴系进行模态分析,求解结束后,结合动画演示得到轴系各阶模态振型。文中只针对轴系一阶弯曲临界问题进行探讨,即只考虑转轴的弯曲振动,不考虑其刚体运动以及转轴的扭转振动。
x方向一阶弯曲模态振型随预载荷系数的变化曲线如图10所示。需要指出的是,文中借鉴文献[10]中图6的数据处理方法,以预载荷取值为0时的转轴中间节点处位移为基准,将所有位移值同时除以该基准,得到各节点处量纲一的相对位移。由图可知,增大预载荷系数可以减小叶轮和下飞轮处的弯曲程度,但会增大转轴中间段的弯曲程度。当预载荷系数取值为0,0.2,0.4时,振型较为一致;当预载荷系数增大到0.6时,振型已有较大偏移。该振型的具体形状与转子的尺寸和轴承的布置情况有关。

图10 模态振型随预载荷系数的变化曲线Fig.10 Variation curve of mode shape with preload factor
3.2 多瓦预载荷调整对临界转速的影响
针对变转速、变载荷、导轴承的预载荷系数取0.3时的核主泵轴系,以工况1为例,描述轴系临界转速的获取方法。首先,以不同工作转速下导轴承的常规8系数作为自变量,对轴系进行模态分析,得到各工作转速对应下的有阻尼固有频率;然后,以工作转速为横坐标,以转速形式的有阻尼固有频率为纵坐标,以过原点的1:1辅助线表示转子工作转速与其有阻尼固有频率相等,交点即为x方向和y方向上的一阶弯曲临界转速,分别为Ωx=2 600.45 r/min,Ωy=5 628.03 r/min(图11)。
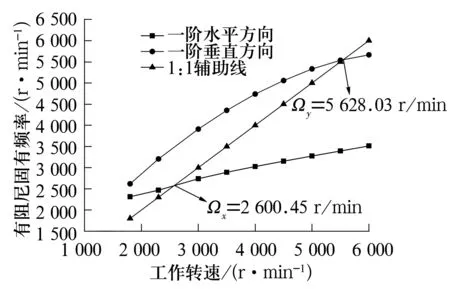
图11 有阻尼固有频率随工作转速的变化曲线Fig.11 Variation curve of damping natural frequency with working speed
考虑到核主泵轴系额定转速只有1 500 r/min,因此只针对Ωx进行研究。Ωx随预载荷系数的变化曲线如图12所示。由图可知:工况1下,当预载荷系数从0增大到0.2时,Ωx略有下降,降低约0.88%;当预载荷系数从0.2增大到0.4时,Ωx缓慢上升,最大提高1.36%;当预载荷系数从0.4增大到0.5、从0.5增大到0.6时,Ωx迅速升高,分别提高了28.06%,48.12%。工况2下,当预载荷系数从0增大到0.1时,Ωx略有下降,降低约0.60%;当预载荷系数从0.1增大到0.4,Ωx缓慢上升,最大提高1.34%;当预载荷系数从0.4增大到0.5、从0.5增大到0.6时,Ωx迅速升高,分别提高了9.42%,27.05%。这是因为当预载荷系数为0~0.4时,导轴承刚度阻尼的增幅较小;当预载荷系数超过0.4时,其刚度阻尼随预载荷系数的增大而迅速增大。

图12 Ωx随预载荷系数的变化曲线Fig.12 Variation curve of Ωx with preload factor
此外,与工况1相比,工况2下的Ωx总是更高一些,这与上文所述2种工况的定义有关。因此,以工况1和工况2作为边界条件来分析轴系一阶弯曲临界转速随预载荷系数的变化。当预载荷系数取值为0~0.4时,临界转速约在2 591.56~3 746.91 r/min;当预载荷系数增大到0.6时,临界转速约在4 990.72~5 263.04 r/min。
现定义同一预载荷系数时2种工况下Ωx的差值为Δx,Δx随预载荷系数的变化曲线如图13所示。由图可知:当预载荷系数为0~0.4时,随预载荷系数的增大,Δx变化不大,均在1 100~1 200 r/min;当预载荷系数超过0.4后,随预载荷系数的增大,Δx急剧减小。
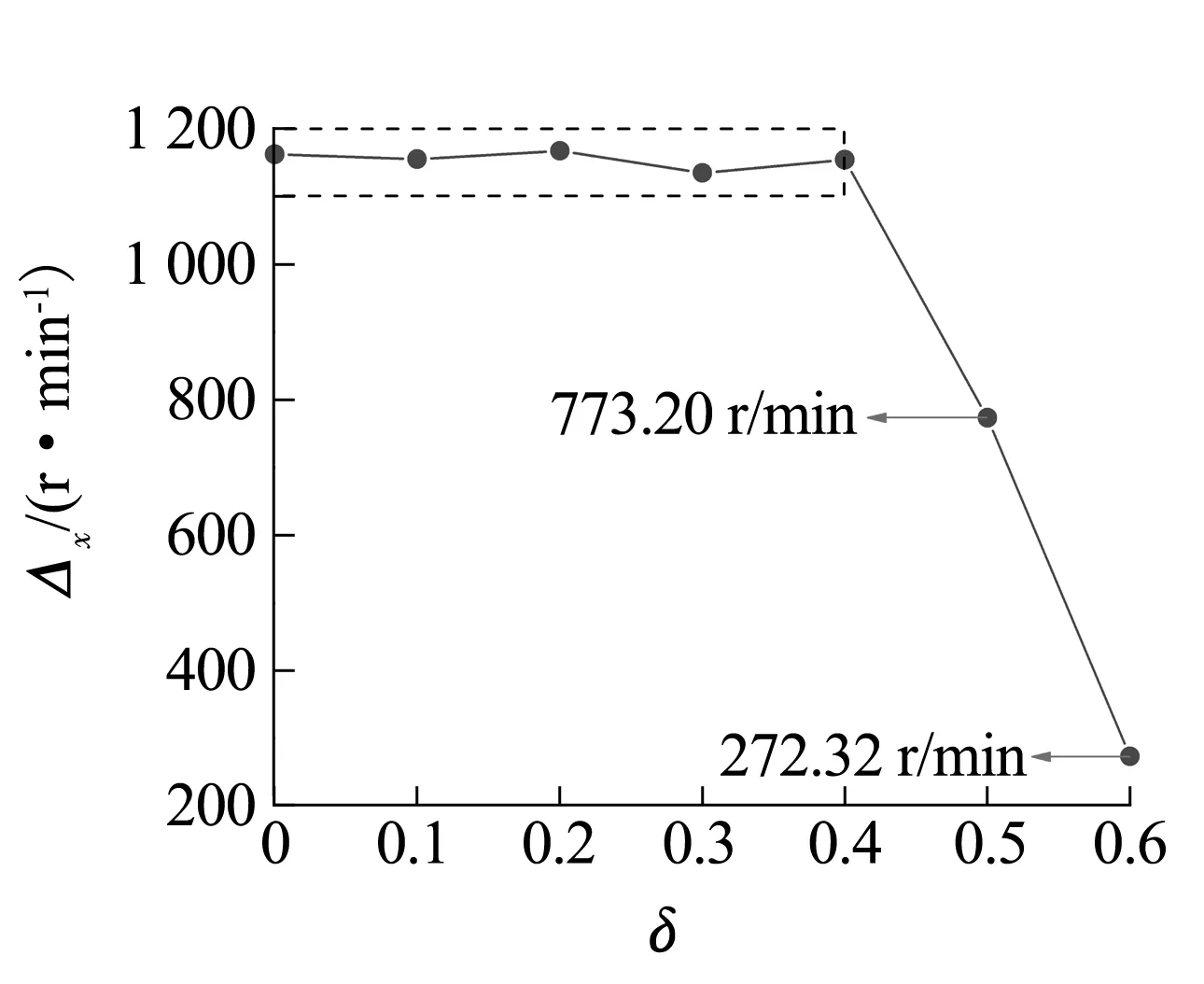
图13 Δx随预载荷系数的变化曲线Fig.13 Variation curve of Δx with preload factor
4 结论
1)从技术操作的角度来考虑,当预载荷系数取0时,有利于轴承安装;从转子动力学的角度来考虑,增大预载荷系数可以减小叶轮和下飞轮处的弯曲程度,提高轴系临界转速;从摩擦学的角度来考虑,当预载荷系数增大至超过0.6时,将导致最小水膜厚度急剧下降而平均温升和功耗迅速升高。因此,对于核主泵转子系统,导轴承的预载荷系数并非越大越好,应根据侧重点的不同进行合理的多瓦预载荷调整,以确保轴系各项性能最优。
2)针对立式核主泵轴系中上、下导轴承的支点位置周向错开45°的问题,采用2种典型瞬态工况作为边界条件来评估轴系临界转速的计算方法,为同类型泵的理论分析提供了重要的参考经验。
3)对于该类型核主泵转子系统,当导轴承的预载荷系数取值超过0.4时,增大预载荷系数可使临界转速迅速增大,同时可使临界转速的范围迅速减小。

