基于Dirichlet过程混合模型的滚动轴承运行状态识别

瞿家明，周易文，王恒，黄希

(南通大学 机械工程学院，江苏 南通 226019)

如果能够在轴承运行过程中及时检测其性能退化的程度、跟踪早期故障，可以有针对性地组织生产和设备维护，有效防止异常失效的发生。

针对滚动轴承的状态监测和退化评估的研究集中在神经网络模型[1]、支持向量机[2]、支持向量数据描述[3]、流形学习[4]等基于数据驱动的方法，但这些方法均无法实时显示数据对应的退化状态阶段。隐马尔科夫模型(Hidden Markov Model,HMM)具有状态隐含、观测序列可见的双重随机属性，很好地描述了设备运行过程中的衰退状态与观测到的征兆信号(如振动、转速和位移等)之间的随机关系，在滚动轴承性能退化评估与预测中得到了广泛应用[5-7]。但HMM在定义和学习过程中需要预设设备所经历的状态数，而实际应用中由于缺乏相应的先验知识，并不能准确地给出模型的退化状态数，限制了HMM的应用场合[8]。

在滚动轴承运行过程中，状态需要随着监测数据的更新而不断更新，如何有效地利用监测数据实现运行状态数的自动识别还需要深入研究。因此，提出了一种基于Dirichlet过程混合模型(Dirichlet Process Mixture Model，DPMM)的状态识别算法，并通过实例验证其有效性和可行性。

1 DP混合模型

Dirichlet过程(Dirichlet Process，DP)是一种典型的非参数Bayes模型[9]，主要用于非参数问题中的先验分布，DP可以拟合任意类型的概率分布，且与多项式分布互为共轭分布，因此在观测值的基础上，DP后验分布便于分析与计算。近年来，DP模型已成为机器学习、文本处理和自然语言处理领域中的研究热点，广泛应用于各种聚类问题的研究中[10-12]。

1.1 DP的定义

假设G0是测度空间Θ上的随机概率测度，参数α为正实数[12]。对于测度空间Θ的任意有限划分A1,A2,…,Ar，若存在如下关系

(G(A1),G(A2),…,G(Ar))～

DDir(αG0(A1),…,αG0(Ar))，

(1)

则G服从由基分布G0和参数α组成的Dirichlet过程，即

G：GDP(α,G0)，

(2)

式中：DDir表示Dirichlet分布。

1.2 DP的构造

在实际应用中往往采用不同形式的构造实现DP的应用。截棍构造(Stick-Breaking Construction，SBC)可以用于独立构造服从DP的随机样本[13]，其设有2个参数：聚集参数α、基础分布G0。随机概率质量πk可以通过如下方式构造：对长度为1的棒在比例β1处切割，并将切掉的这部分长度赋值给π1，而后对剩余长度为(1-β1)的棒在其比例β2处切割, 并将切掉的棒的长度赋值给π2，然后按照相同的方式对剩余的棒在比例βk处切割,并将切掉的棒的长度赋值给πk，记为πk：GEM(α)，如图1所示。

图1 SBC示意图Fig.1 Diagram of SBC

随机概率分布G构造为

(3)

其中，随机概率质量πk通过以α为参数的β分布产生，随机原子序列θk从基础分布G0抽样。

与SBC类似，中国餐馆过程(Chinese Restaurant Process,CRP)构造如下[13]：设中国餐馆内可以容纳无限多张桌子，所有桌子上都贴上标签1,2,…,K，进入餐馆的顾客可以挑一张桌子坐下。θi被比作第i个进入餐厅的顾客，而不同的φk值表示餐桌。第1个顾客以概率1就座于一张新桌子，第i个顾客以概率mn/(n-1+α)就座于一张已坐下mn个顾客的旧桌子，n为进入餐馆的顾客总数；或以概率α/(n-1+α)就座于一张新桌子，即K增加1，而φk:G0,θi=φk，如图2所示，圆圈代表桌子，方框代表进入餐馆的顾客。

图2 CRP构造示意图Fig.2 Construction diagram of CRP

从Dirichlet过程的构造可以看出, 无论哪种方式, 均体现了其良好的聚类性质。

1.3 DPMM

DP表现了良好的聚类性质，但其只能将具有相同值的数据聚为一类，如果2组数据不相等，不管两者间的相似性多强，利用DP均无法实现聚类，因此就需要引入DPMM[13]。在DPMM中，DP作为参数的先验分布存在，假设观测数据为xi，其分布服从

(4)

式中：F(θi) 为观测数据xi服从以θi为参数的分布；当G服从Dirichlet分布时，该模型称为Dirichlet过程混合模型。

2 基于DPMM的滚动轴承状态数识别算法研究

基于DPMM的滚动轴承状态数识别算法流程如图3所示，其具体步骤如下：

图3 基于DPMM的滚动轴承状态识别算法流程Fig.3 Flow chart of algorithm for state recognition of rolling bearing based on DPMM

1) 对轴承振动数据进行特征提取；

2) 随机初始化DPMM的参数，即初始聚类数目N、迭代次数M和聚集参数α；

3) 构造观测序列，使其服从Gaussian分布或多项式分布；

4) 观测序列分布参数服从Gaussian-Wishart分布或DP分布；

5) 通过截棍过程、中国餐馆过程构造获得Dirichlet先验分布；

6) 通过Gibbs抽样实现参数后验更新，当某个类簇中元素个数为0时，N减1，继续迭代步骤5～6，待聚类数目稳定时停止迭代，获得轴承最终运行状态数N。

将轴承观测数据作为DPMM的输入，记为o1,o2,…,on，则

(5)

假设观测序列服从Gaussian分布O～Nd(μ,S)，其参数服从共轭分布Gaussian-Wishart分布μ,R～Wd(m,S)，每个分布都具有相同的超参数和各自的参数。其中，轴承数据任意分组，维数为d，均值为μ，均方差为S，相关系数为R；轴承数据服从分布参数的维数为v，均值为m，均方差为S，相关系数为r。

假设观测数据服从Gaussian分布，即

(6)

多组数据似然函数为

p(O丨μ,R)=(2π)-nd/2|R|n/2·

(7)

参数服从Gaussian-Wishart分布，即

p(R)=2-vd/2π-d(d-1)/4|S|v/2|R|(v-d-1)/2·

(8)

(9)

(10)

根据Bayes公式，观测数据及其分布参数的联合概率可以表示为似然函数与参数先验的乘积，也可表示为后验分布与边缘函数的乘积，即

p(μ,R,O)=p(O|μ,R)·p(μ,R)=

p(μ,R|O)·p(O)。

(11)

观测数据和分布参数的联合概率为

(12)

利用Gibbs采样实现后验参数的更新

(13)

轴承观测数据的边缘概率为

(14)

由(12)，(13)和(14)式推导出后验分布公式为

(15)

(9)式与(15)式具有相同的分布形式，对比可知后验分布的更新意味着超参数(r,v,m,S)的更新。在(14)式中，需要计算Γ项的比率以及|S|和|S″|的值。为简化计算，假设更新前后v不变，将(14)式进行Γ项扩展得

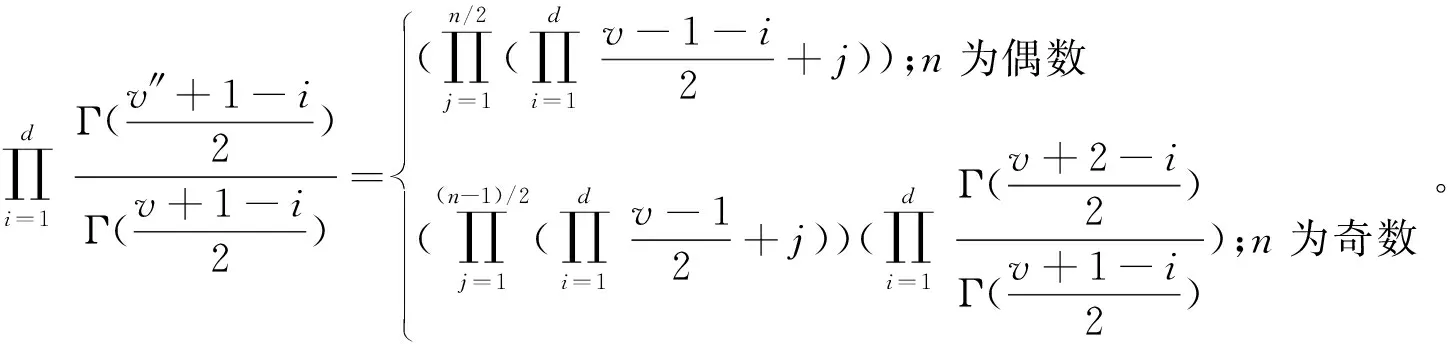
(16)

通过Gibbs采样实现参数后验更新，在每个类簇中每次增加(或减少)1个观测序列，利用Cholesky分解更新S的值，然后根据新的参数值计算每个类簇的似然概率。在迭代过程中，不断更新每个类簇的均值和方差，若类簇中的值为空，则类簇总数减1，否则将继续迭代更新。DPMM算法不依赖于训练样本，而且随着观测数据的变化，模型结构能够自适应调整，从而实现动态聚类，自动识别轴承的运行状态。

3 实例研究

为验证DPMM算法的有效性与可行性，对滚动轴承状态监测数据[14]进行验证和分析，选择负载0 kW，转速1 797 r/min下SKF6205-2RS型轴承的振动加速度数据。采用电火花加工对轴承进行破坏，故障直径分别为0.177 8，0.355 6，0.533 4和0.711 2 mm，轴承基本参数及其运行状态分别见表1和表2。将轴承正常状态数据和4种人为制造的状态数据分别取容量相同的样本相互连接作为观测数据。

表1 试验轴承技术参数Tab.1 Technical parameters of test bearing

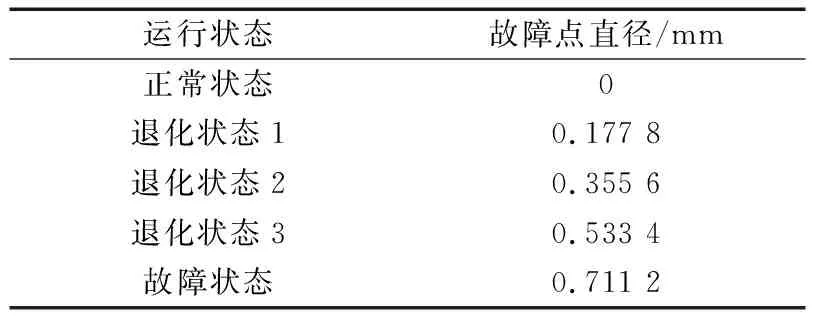
表2 滚动轴承运行状态划分Tab.2 Partition of operation states of rolling bearing

在DPMM算法中，设初始聚类数N=100，聚集参数α=20，迭代次数M=300，取轴承峭度指标作为观测数据构造观测序列服从Gaussian分布，参数服从Gaussian-Wishart分布，通过SBC和CRP分别构造DP过程。基于DPMM的滚动轴承运行状态识别结果如图4所示，经过300次的迭代，聚类结果趋于稳定且收敛到5，与已知的滚动轴承状态数(表2)相一致，说明DPMM模型能够有效识别滚动轴承运行状态，为轴承退化评估与寿命预测提供了一种新方法。

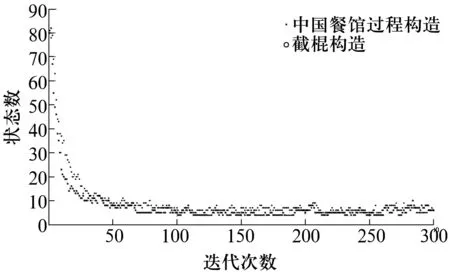
图4 基于峭度指标的轴承运行状态数识别结果Fig.4 Recognition result of number of operation states of bearing based on kurtosis index

聚集参数α不同取值时的聚类结果如图5所示，从图中可以看出，无论参数α的初始值如何选取，该模型聚类结果均能收敛到相同的值。进一步分析特征值的选择对识别结果的影响，取轴承均方根作为观测数据，其他参数不变，基于DPMM的运行状态数识别结果如图6所示。

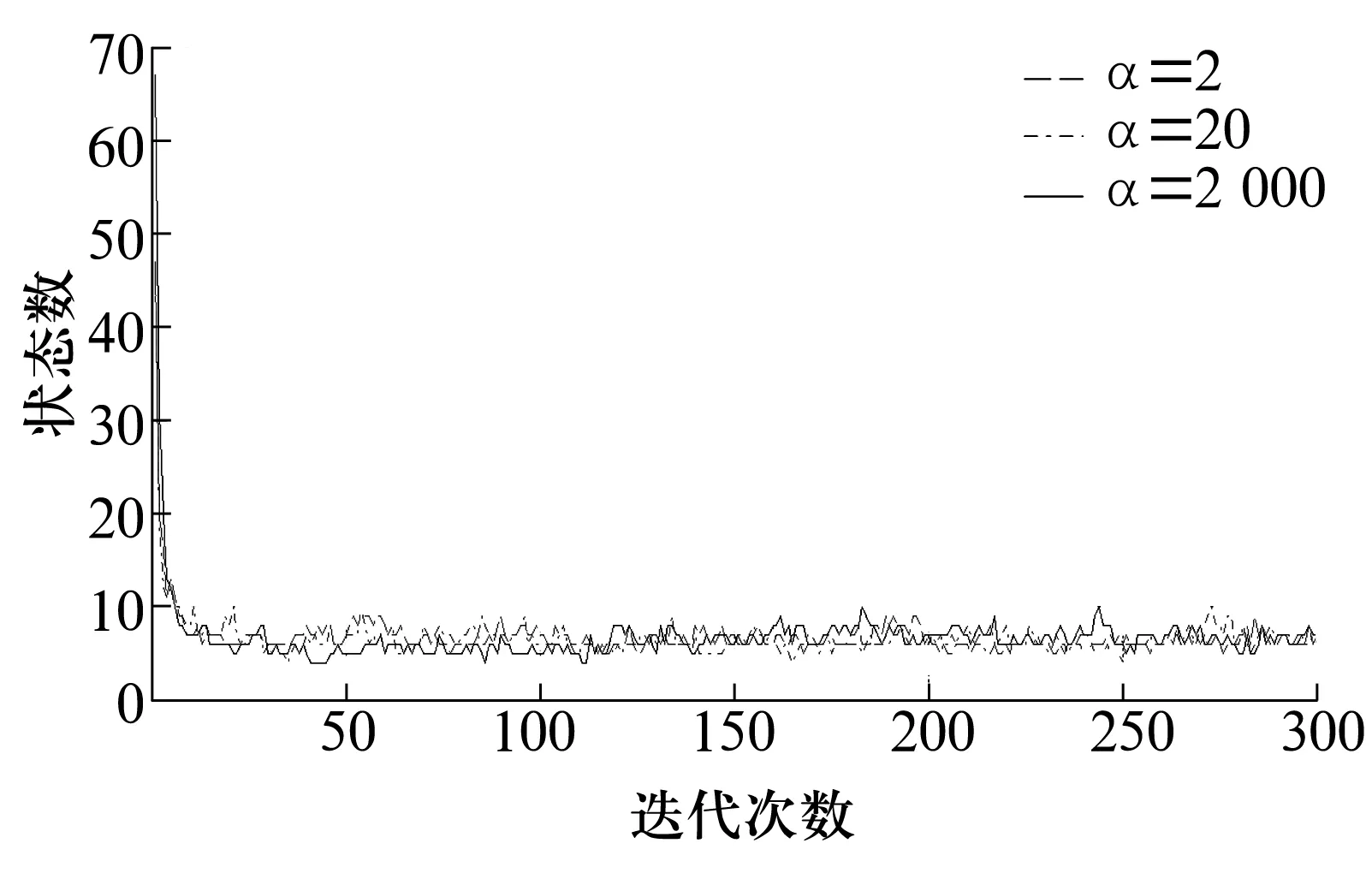
图5 不同α值的聚类结果Fig.5 Clustering results of differentα

根据图4及图6的结果，对峭度指标和均方根分别获得滚动轴承运行状态数进行统计分析，获得其概率直方图(图7)，从图中可以看出，状态数聚类为5的概率最大，可以认为最终状态数为5。

图6 基于均方根的轴承状态数识别结果Fig.6 Recognition result of number of states of bearing based on RMS

图7 状态数聚类结果概率直方图Fig.7 Probability histogram of clustering results of number of states

综合分析可得：构造方法不影响结果的稳定性，参数α不同取值时均能快速实现聚类，结果稳定。DPMM算法对于参数的预设没有要求，也不依赖滚动轴承特征值、聚集参数等初始参数的选择，具有很强的适应性和稳定性。

4 结束语

故障诊断算法中退化状态数的确定一直以来依靠的是设备维护的经验。这对于算法实现设备退化过程描述和观测数据的处理带来了一定的困难。DPMM抛开传统经验，利用数据自身的特性进行聚类，为进一步分析设备退化过程以及每个阶段的退化研究提供了一种新的方式。

初始参数的选择是模型训练的难点，其影响着模型收敛的速度和准确性。DPMM引入了Bayes聚类算法，从另一个角度实现了参数需要人为预先设定的问题，从数据分析的角度也有利于模型的收敛速度和准确性，解决了模型参数预设的问题。另外，DPMM能够随着数据变化实现自适应调整，避免了故障诊断过程中数据变化而模型不变进而可能出现的预测错误，具有一定的研究价值。