弹流润滑条件下的深沟球轴承径向刚度及油膜厚度分析
杨杰,买买提明·艾尼,2,王晓亮,武园园,王国建
(1.新疆大学 机械工程学院,乌鲁木齐 830049;2.西安交通大学 结构强度和振动国家重点实验室,西安 710049)
深沟球轴承摩擦因数小、极限转速高,且非常耐用,无需经常维护,常应用于精密仪表、变速箱、电动机中,是该类机械的重要传动部件。深沟球轴承径向刚度直接影响着转子的动力学特性,故有必要对其径向刚度进行研究。文献[1-8]均有关于轴承的径向刚度的计算,但计算均基于Hertz接触理论,轴承处于干摩擦状态,未考虑油膜润滑的影响。文献[9]通过试验证明了润滑油膜会影响深沟球轴承的刚度;文献[10]基于流固耦合法对滚动轴承的刚度进行分析;文献[11]阐述了弹流润滑会对滚动轴承接触刚度产生影响。鉴于此,考虑油膜润滑的影响建立深沟球轴承综合径向刚度数学模型,并基于C++编写计算轴承径向刚度的程序,分析轴承载荷、转速以及润滑油黏度对轴承径向刚度的影响。
1 深沟球轴承径向刚度数学建模
在润滑油充盈时,深沟球轴承的钢球被油膜抬起,外圈刚度由钢球与外圈沟道的Hertz接触刚度和油膜刚度串联组成,内圈刚度由钢球与内圈沟道的Hertz接触刚度和油膜刚度串联组成。滚动轴承的综合刚度由内、外圈刚度串联而成[12]。
1.1 Hertz接触刚度
滚动轴承的接触刚度指轴承内外圈产生单位位移所需的外载荷,仅受纯径向载荷且无径向游隙的深沟球轴承,如图1所示,在“偶压”状态下,钢球最大载荷Qmax与径向载荷Fr之间的关系为[13]40-42
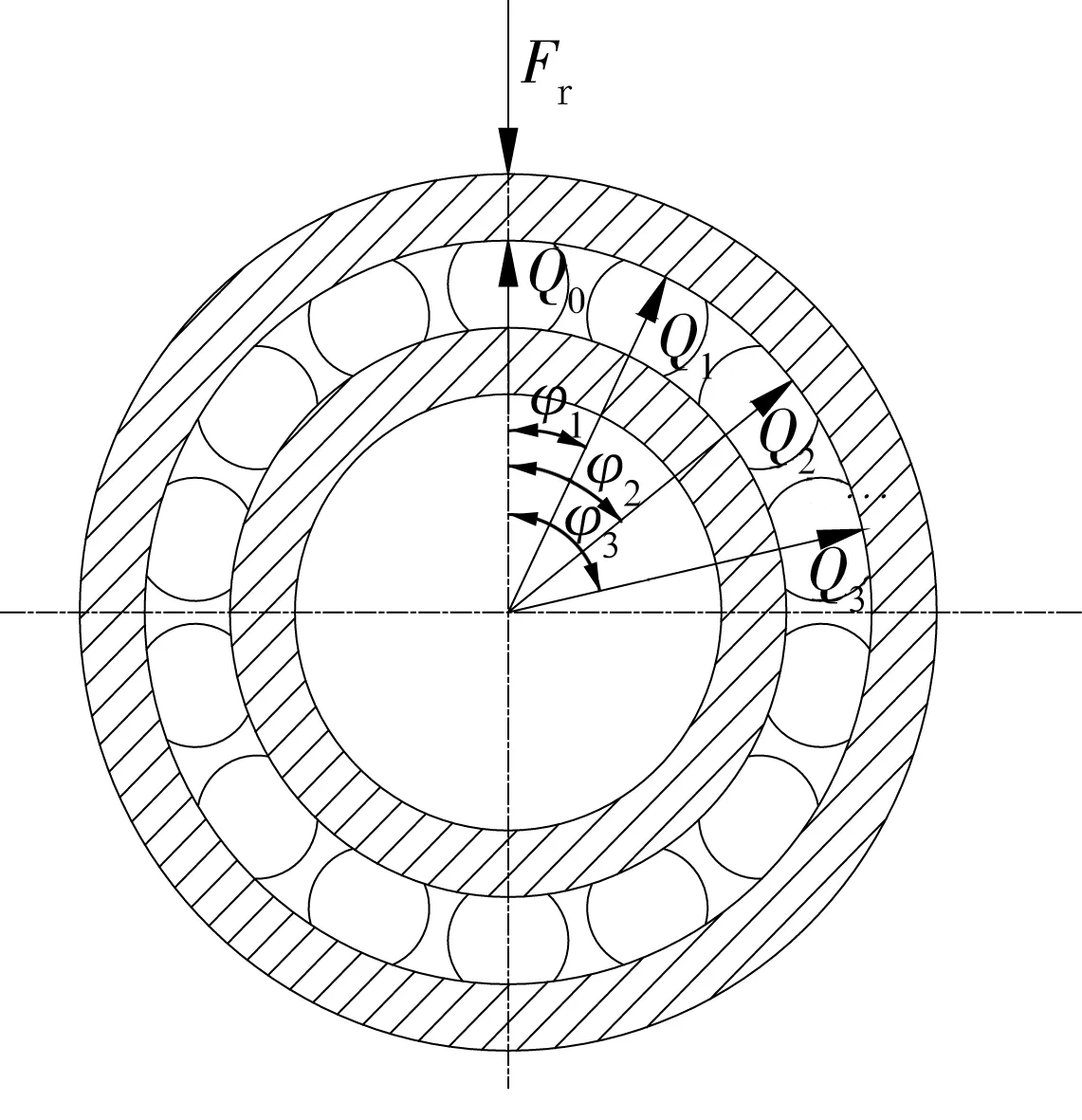
图1 深沟球轴承的径向载荷示意图Fig.1 Diagram of radial load of deep groove ball bearing
(1)
式中:Z为钢球数量;φj为钢球的方位角。
在纯径向载荷作用下,深沟球轴承仅在径向方向产生位移,其径向位移可用最大接触载荷处套圈法向弹性变形表示,即
(2)
γ=Dw/Dpw,
式中:ν1,ν2分别为钢球与套圈材料的泊松比;E1,E2分别为钢球与套圈材料的弹性模量;F(e),E(e)分别为第一类和第二类完全椭圆积分函数;e为椭圆参数;Qmax为套圈最大接触载荷。对于内圈,±取+,对于外圈,±取-;Dw为钢球直径;Dpw为球组节圆直径;f为套圈沟曲率半径系数。
根据文献[13]10-13可知椭圆参数为
e=(1-1/k2)1/2,
(3)
k=1.033 9(Ry/Rx)0.636 0,
对于内圈,±取+,对于外圈,±取-。第一类和第二类完全椭圆积分函数为
F(e)=1.527 7+0.601 3ln(Ry/Rx),
(4)
E(e)=1.003+0.596 8(Rx/Ry)。
通过(1)~(4)式可得
(5)
由(5)式可得钢球与套圈沟道的Hertz接触刚度为
(6)
1.2 弹流润滑油膜刚度
大多数滚动轴承工作在润滑状态,深沟球轴承工作时钢球与沟道之间会充满润滑油,接触区域会处于弹流润滑状态(EHL),且弹流引起的油膜刚度会对轴承的刚度产生重要影响。
Hamrock-Dowson采用数值计算法得出等温椭圆接触的点接触中心油膜厚度[14],将中心油膜厚度量纲一化为
(7)
G=αE′,
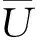
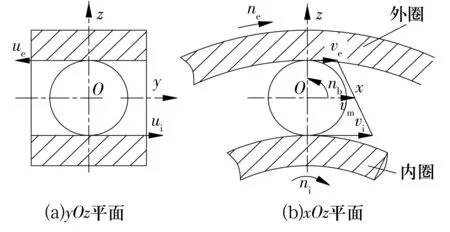
图2 钢球与内外圈接触表面速度Fig.2 Surface speed of contact between steel ball,inner and outer rings
假设深沟球轴承外圈固定,内圈旋转,钢球与内圈沟道的接触点在x,y方向的速度分别为ui,vi,钢球与外圈沟道的接触点在x,y方向的速度分别为ue,ve。
外圈固定,则外圈转速ne为0。钢球公转速度为
(8)
式中:ni为内圈转速。
由于钢球的自转,钢球与内、外圈沟道接触点的速度相同,即
(9)
则钢球与内、外圈沟道接触点的平均速度为
(10)
由(7),(10)式可得中心油膜厚度为
(11)
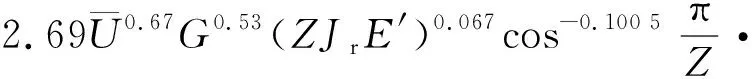
钢球与套圈沟道接触的油膜刚度为
(12)
1.3 深沟球轴承综合径向刚度
轴承内、外圈刚度分别为
(13)
轴承刚度由内、外圈刚度串联得到
(14)
2 计算流程
轴承综合径向刚度受转速、润滑油黏度及载荷的影响。基于C++编写计算轴承径向刚度的程序,流程图如图3所示。主要步骤如下:
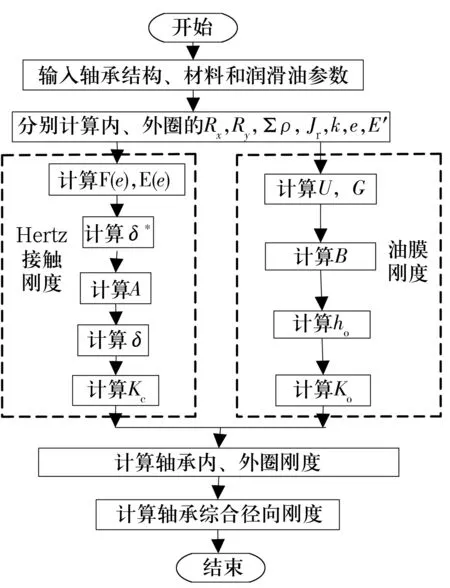
图3 轴承综合径向刚度计算流程图Fig.3 Flow chart for calculation of synthetical radial stiffness of bearing
1)输入轴承结构、材料和润滑油参数;
2)分别计算钢球与内、外圈接触的Hertz接触刚度和油膜刚度;
3)内、外圈径向刚度由钢球与套圈沟道接触的Hertz接触刚度和油膜刚度串联而成,计算内、外圈径向刚度;
4)轴承综合刚度由内、外圈刚度串联而成,计算轴承综合径向刚度。
3 实例分析
以深沟球轴承6003为例分析,其主要结构参数见表1。润滑油黏度为0.02 Pa·s,黏压系数为2.3×10-8Pa-1。内外圈和钢球材料均为GCr15,其材料参数为:弹性模量为207 GPa,泊松比为0.3。

表1 主要结构参数Tab.1 The main structural parameters
3.1 径向载荷对轴承综合径向刚度和油膜厚度的影响
在分析深沟球轴承时,忽略转动过程中温度对轴承刚度的影响。在转速为5 000 r/min-1,润滑油黏度为η=0.02 Pa·s,黏压系数α=2.3×10-8Pa-1时深沟球轴承的综合径向刚度和中心油膜厚度随径向载荷的变化如图4所示。由图可以看出,随径向载荷增大轴承刚度增大。在载荷为0~1 700 N时,轴承的综合径向刚度和中心油膜厚度分别急剧增大和减小,当载荷超过1 700 N时,两者均变化缓慢。
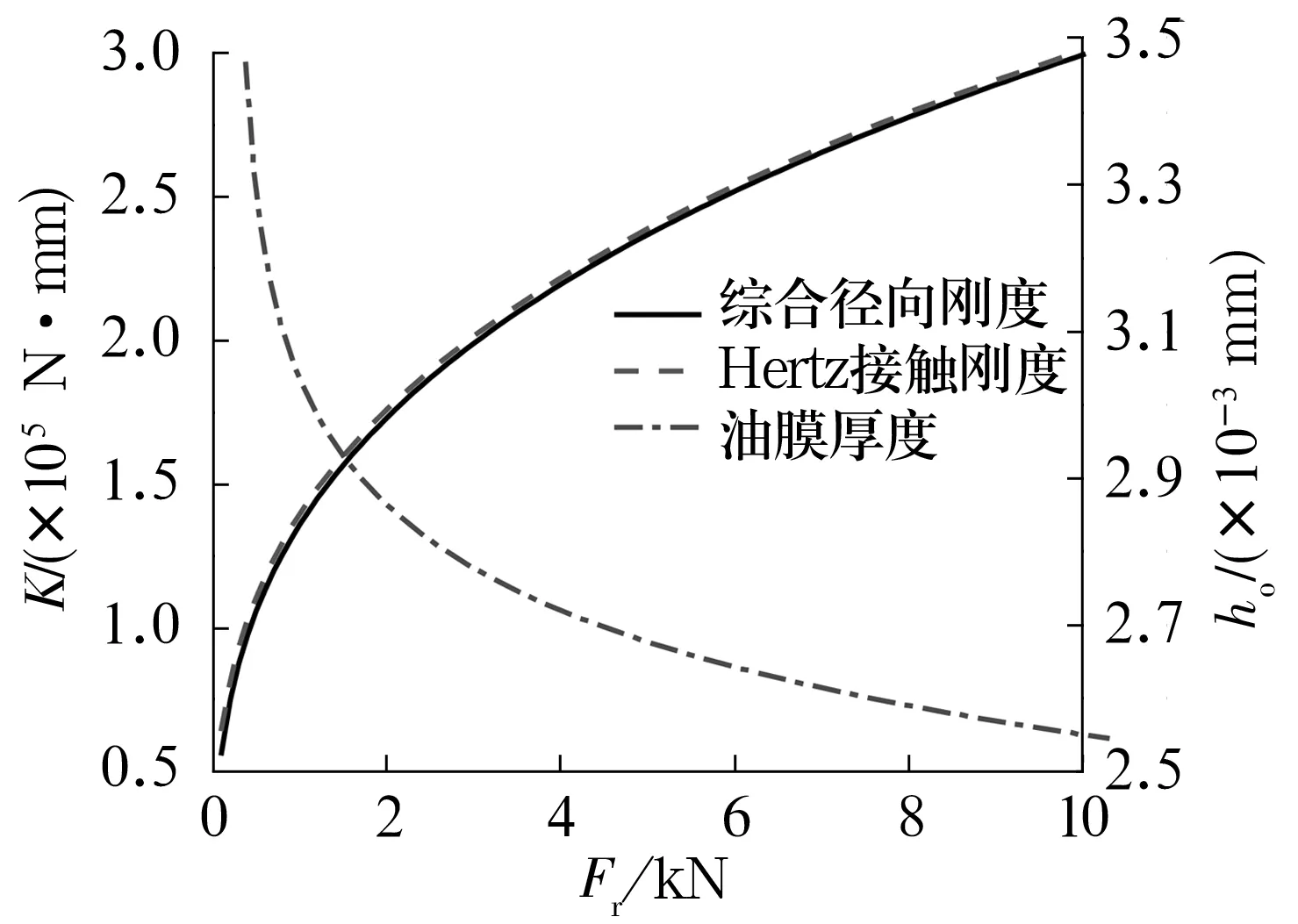
图4 径向载荷对轴承综合径向刚度和油膜厚度的影响Fig.4 Effect of radial load on synthetical radial stiffness and oil film thickness of bearing
在考虑油膜情况下,轴承的综合径向刚度略小于单纯Hertz接触刚度。为便于分析,定义接触刚度与综合径向刚度之差为刚度差ΔK,其随径向载荷Fr的变化如图5所示。由图可以看出,载荷小于1 kN时,刚度差变化较大,油膜对轴承刚度影响较大;载荷大于1 kN时,油膜对轴承的刚度影响小。
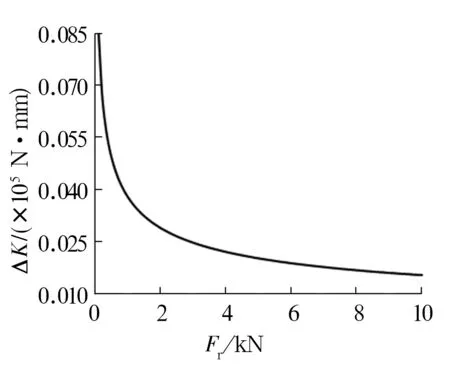
图5 径向载荷对轴承综合径向刚度差ΔK的影响Fig.5 Effect of radial load on synthetical radial stiffness difference of bearing ΔK
3.2 转速和润滑油黏度对轴承综合径向刚度和油膜厚度的影响
在径向载荷Fr=1 kN的情况下,转速和润滑油黏度对深沟球轴承综合径向刚度和油膜厚度的影响如图6所示。由图可以看出,转速接近0时,润滑剂黏度对轴承的综合径向刚度和油膜厚度影响较小,随转速增大,轴承的综合径向刚度和油膜厚度分别呈减小和增大趋势。转速越大对二者的影响越大;相同转速下随润滑油黏度增大,轴承的综合径向刚度减小,而油膜厚度增大。
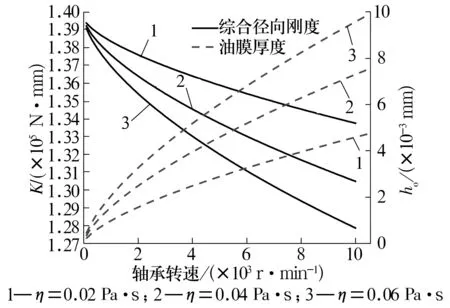
图6 转速和润滑油黏度对轴承综合刚度和油膜厚度的影响Fig.6 Effect of rotational speed and viscosity of lubricating oil on synthetical stiffness and oil film thickness of bearing
4 结束语
考虑油膜润滑的影响建立了深沟球轴承综合径向刚度数学计算模型,分析了径向载荷、转速、润滑油黏度对轴承综合径向刚度的影响。结果表明:径向载荷、转速、润滑油黏度均会对轴承径向刚度产生重要影响,在分析轴承运动学特性时应考虑润滑油的作用,而不应只考虑干摩擦的状态。分析结果可为该类轴承的设计提供参考。

