Hertz点接触参数的工程计算方法
杨咸启,荣超,邹星波
(1.黄山学院,安徽 黄山 242700;2.安徽日飞轴承有限公司,安徽 铜陵 244000)
在球轴承零件受力分析时,需考虑2个零件的相互接触力,该接触力通常为Hertz点接触应力分布。Hertz点接触是指在空载状态下2个物体初始接触为一个点的二次光滑曲面的接触。在计算接触力的大小时首先要利用接触表面的曲率系数,再计算椭圆积分函数,但该计算过程相对复杂[1-4]。鉴于此,给出了近似的Hertz点接触参数的近似计算方法,从而方便分析接触应力分布情况。
1 Hertz点接触参数理论计算方法
一般Hertz点接触模型和接触区域如图1所示。分析接触应力时需要计算的接触参数有:接触区域椭圆长、短半轴和2个接触体的弹性趋近量。
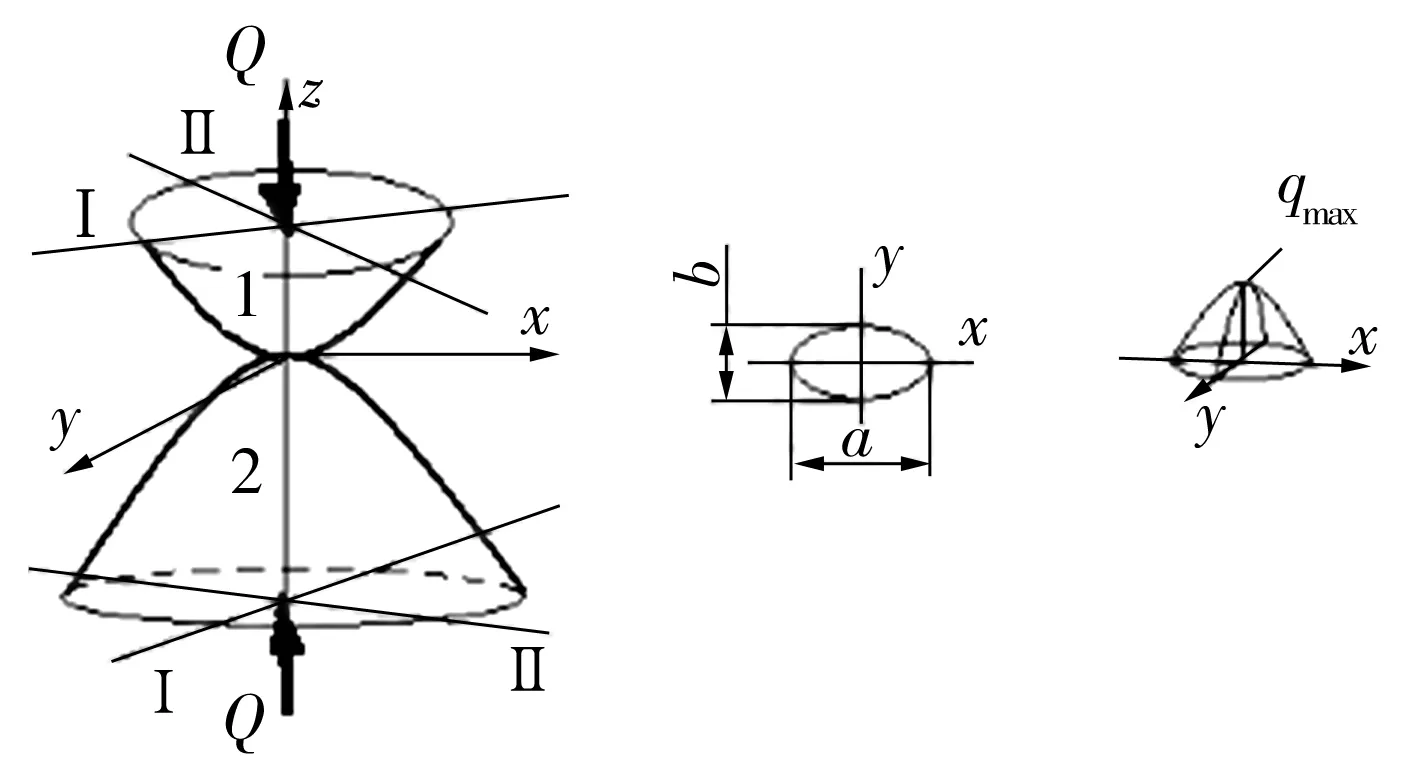
图1 Hertz点接触模型Fig.1 Hertzian point contact model
利用弹性力学接触理论,可以得到点接触区域上的表面压应力分布为[4]
(1)
式中:a,b分别为接触区域椭圆长、短半轴;Q为法向接触载荷。
假设相互接触的轴承零件材料均为GCr15,其弹性模量E=207 GPa,泊松比ν=0.3, 则接触椭圆长、短半轴分别简化为
(2)
(3)
式中:F(e),E(e)分别为第一、二类完全椭圆积分;e为接触椭圆率;∑ρ为曲率和函数;对于凸面±取+,对于凹面±取-;RⅠ1,RⅠ2分别为接触体1,2在第Ⅰ主曲面内接触点的曲率半径;RⅡ1,RⅡ2分别为接触体1,2在第Ⅱ主曲率面内接触点的曲率半径。
2个接触体的弹性接触趋近量为
δ=2.791×10-4δ*(Q2∑ρ)1/3,
(4)
为了计算接触区域参数,需要采用曲率比函数,即
(5)
式中:ρⅠ1,ρⅠ2分别为接触体1,2在第Ⅰ主曲面内接触点的主曲率;ρⅡ1,ρⅡ2分别为接触体1,2在第Ⅱ主曲率面内接触点的曲率。
曲率比函数又可表示为
(6)
当已知接触表面的主曲率后,首先计算出F(ρ),再定出接触椭圆率e。进一步计算出第一、二类完全椭圆积分F(e),E(e)及a*,b*,δ*,但该计算过程复杂。实际工程问题计算中是给定参数e计算出F(e),E(e),将计算结果制成图表。利用图表直接查找和插补方法来进行快速近似计算。
2 点接触参数近似计算方法
由于理论计算方法过程复杂,主要步骤是确定接触椭圆偏心率及椭圆积分,再通过(2)~(4)式确定接触参数a,b,δ,最终得到接触应力分布情况。下面介绍3种接触椭圆率及椭圆积分的近似计算方法。
将接触区域的主曲率面设为坐标面,第Ⅰ主曲率面内包含y轴方向(接触椭圆短轴方向),第Ⅱ主曲率面内包含x轴方向(接触椭圆长轴方向)。将接触点处的综合曲率表示为
1/Rx=ρx1+ρx2,
(7)
1/Ry=ρy1+ρy2,
(8)
ρx1=ρⅡ1,ρx2=ρⅡ2,ρy1=ρⅠ1,ρy2=ρⅠ2,
式中:Rx,Ry为接触体表面的综合曲率半径参数;ρx1,ρx2,ρy1,ρy2为接触体的主曲率面内接触点的曲率。
由(5)式可得曲率比函数为
(9)
显然,这里要求Rx>Ry。
2.1 第1种近似计算方法
根据文献[4],接触椭圆半轴比值和椭圆积分的近似计算方法为
(10)
(11)
(12)
(13)
通过(11)~(13)式可得到接触椭圆率及椭圆积分。在上面的计算过程中,需要注意接触区域的长轴和短轴与坐标轴之间的位置对应关系。
2.2 第2种近似计算方法
文献[5-6]给出了接触椭圆率e的一种近似计算方法,即
,(14)
通过(14)式计算出e后,再对椭圆积分进行近似计算,即
F(e)≈1.386 294 4+0.111 972 3(1-e2)+
0.072 529 6(1-e2)2-
[0.5+0.121 347 8(1-e2)+
0.028 872 9(1-e2)2]ln(1-e2),
(15)
E(e)≈1.0+0.463 015 1(1-e2)+
0.107 781 2(1-e2)2-
[0.245 272 7(1-e2)+
0.041 249 6(1-e2)2]ln(1-e2),
(16)
通过(14)~(16)式可得到接触椭圆率及椭圆积分。利用此方法计算时需要注意0 (14)式计算过程还是比较复杂,且参数F(ρ)趋近于零时为一种不定式,需要取更多的项才能准确计算F(e),E(e)值。为避免不定式计算,对椭圆积分进行变换,即 (17) (18) 令 (19) 则 E(e)=(1-e2)F(e)+e2Δ(e)。 (20) 上面各式中,e的取值范围为0≤e≤1,则π/2≤F(e)<∞,1≤E(e)≤π/2 ,π/4≤Δ(e)≤1。 由(6)式经变换可得 (21) 将(20)式代入(21)式可得 (22) (22)式表示椭圆率与椭圆积分和曲率比函数的关系。利用这种曲率比函数关系,对e,F(e),E(e)进行近似计算如下 (23) (24) (25) 通过(23)~(25)式可得到接触椭圆率及椭圆积分。利用此方法计算时,允许0≤F(ρ)≤1。 以某深沟球轴承为例,采用上节介绍的近似方法进行接触参数计算,其中的接触模型如图2所示。轴承主要结构参数为:球径Dw=22 mm,球组节圆直径Dpw=162 mm,内、外沟曲率半径系数fi= 0.515,fe= 0.520,接触角α=0。 图2 深沟球轴承接触模型Fig.2 Contact model of deep groove ball bearing 在内圈沟道接触点处 (26) (27) (28) (29) γ=Dwcosα/Dpw。 在外圈沟道接触点处 (30) (31) (32) (33) 通过(26)~(33)式,可得Rx,Ry,F(ρ),见表1。 表1 Rx,Ry,F(ρ)的计算结果Tab.1 Calculated results of Rx,Ry,F(ρ) 再用上述3种近似计算方法计算e,F(e)和E(e),结果见表2。3种近似计算的接触椭圆率e比较接近,而第1种和第2种近似计算方法的F(e),E(e)较接近,第3种计算方法计算过程更为简化一些。 表2 e,F(e),E(e)的计算结果Tab.2 Calculated results of e,F(e),E(e) 介绍了Hertz点接触的理论计算方法,将Hertz点接触参数计算过程进行了近似计算。拟合出Hertz点接触曲率函数与接触椭圆偏心率e、椭圆积分之间的关系函数。在接触计算工程中省去了复杂的计算过程,使得接触计算变得相对简化。最后以深沟球轴承为例进行实例分析,并对比分析了3种近似计算方法。说明介绍的近似方法是有效的。2.3 第3种近似计算方法
3 实例分析
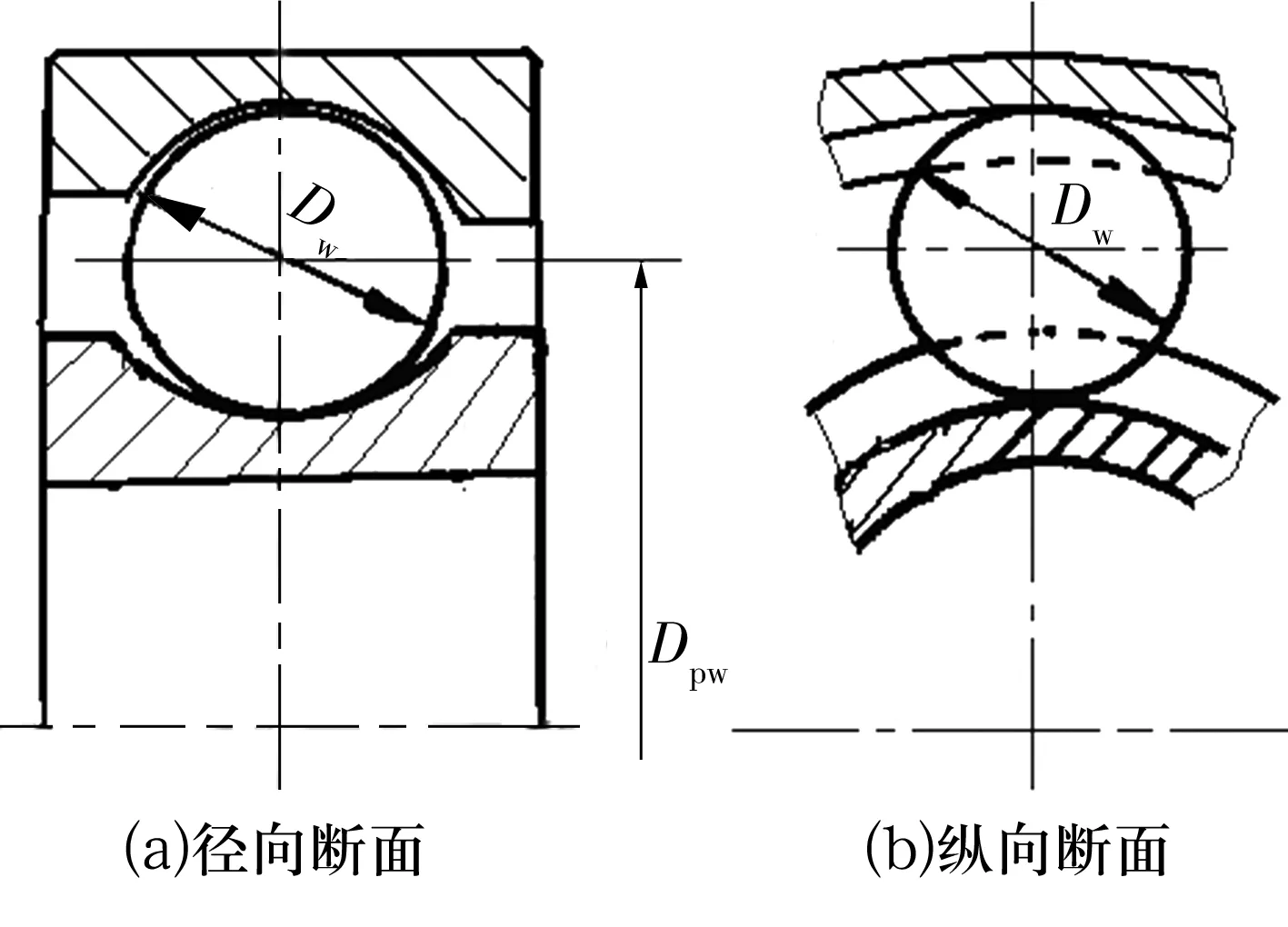

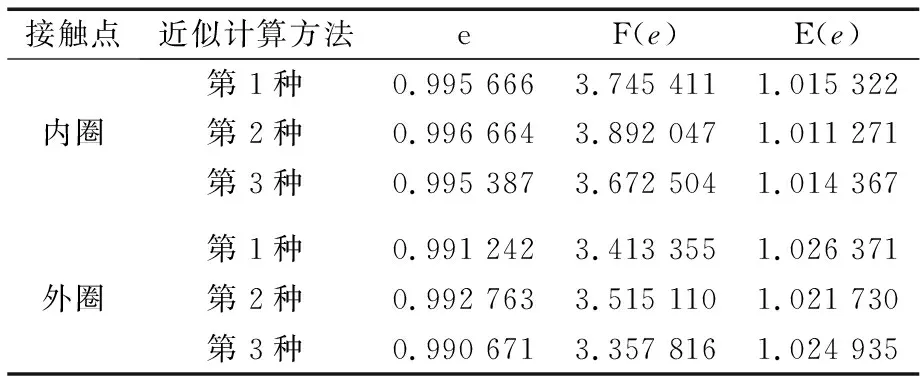
4 结束语
——对2018年广州市一道中考题的研究

