有关抛物线切线与焦点的一些性质

王 庆

(苏州市职业大学 数理部，江苏 苏州 215104)

近年来，作者用射影几何的方法给出了二次曲线的一些有趣的性质，其中，部分内容写成本文及《抛物线的一些性质》[1]。研究发现，有些平面几何问题用射影几何研究更自然、条理更清楚，而用平面几何方法处理则有难度。本文继续用射影几何的方法讨论抛物线的性质，特别是由抛物线的两条切线与焦点得到的相似三角形的性质，用到的射影几何知识可参看[2-4]或其它高等几何书籍。本文讨论的部分问题来源于文献[4]。

1 主要结果与证明

先给出一个在讨论二次曲线问题时常用的性质。

性质1 设抛物线的切线交两定切线于X,X′，点F是焦点，则∠XFX′是定角。

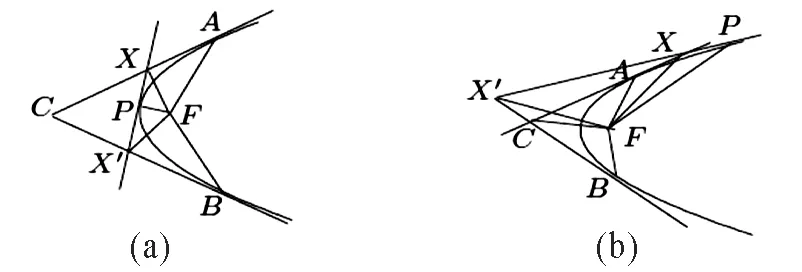
图1 抛物线的切线交两定切线图：(a)X;(b)X′

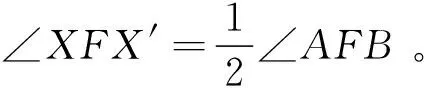
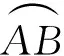
∠X′FC=∠X′FB-∠CFB=∠X′FP-∠CFA=∠X′FP-∠X′FC-∠X′FA=-∠X′FC+∠AFP，

性质 2 设抛物线上点A,B处切线交于C，F是焦点，则ΔACF,ΔCBF相似。如果X,X′是抛物线上切线与CA,CB的交点，则ΔXX′F也与ΔACF,ΔCBF相似。

证 图2画出了A,B在抛物线上不同位置的图形，分别对应于A,B在抛物线对称轴的同一侧或两侧。设抛物线的顶点D处切线交CA,CB分别于E,G。由于C是A,B处切线的交点，F是抛物线的焦点，∠CFA=∠CFB；类似有∠DFE=∠EFA, ∠DFG=∠GFB。E,G分别是抛物线顶点D处切线与A,B处切线的交点，由 [2] §4.4例5，FE⊥AE,FG⊥GB，四点C,E,F,G共圆，故有∠BCF=∠GEF[2]。而ΔAEF与ΔDEF相似，∠EAF=∠DEF=∠FCG，即∠CAF=∠FCB。这些证明了ΔACF与ΔCBF相似。

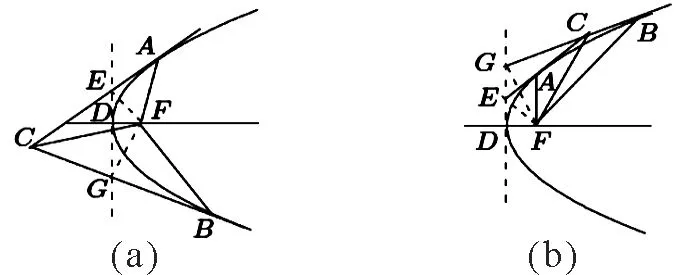
图2 抛物线上的点A，B在抛物线上 不同位置的图:(a)A;(b)B

ΔXX′F与ΔACF,ΔCBF的相似容易证明。

下面的性质说明抛物线也可以由性质2中相似三角形确定。

性质 3 设平面上ΔBCF与ΔCAF相似，点B,A在线段CF的两侧。则有与直线CB,CA分别切于B,A, 以F为焦点的抛物线。

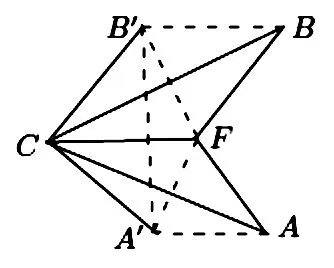
图3 △BCF与△CAF相似

证 如图3，ΔBCF与ΔCAF相似，设B′,A′分别是F关于CB,CA的对称点。于是BB′=BF,AA′=AF, ∠CB′B=∠CA′A=∠CFB=∠CFA，而CB′=CF=CA。从这些关系可得：

由性质2、性质3可得已知抛物线的焦点F及它的一条切线及其上切点A作抛物线的其它切线与切点的方法。 也可以得到已知抛物线的两条切线及其上切点作抛物线的焦点、准线的方法。

性质 4 在抛物线上点A处切线上取两点P,Q使PF=FQ，设R是过P,Q的切线的交点。则RF是抛物线的对称轴。

图4 抛物线上一点处切线上取两点情形1 图5 抛物线上一点处切线上取两点情形2

证 如图4或图5，设过P,Q的切线上切点分别是C,D。由PF=FQ可得∠APF=∠AQF。由性质2有许多相似三角形：

ΔCPY与ΔPAF；ΔAQF与ΔQDF；ΔCRF与ΔRDF。

因此，∠RCF=∠RDF, ∠CRF=∠FRD,ΔCRF与ΔDRF全等，C,D关于RF对称。而R是抛物线上弦CD的极点，这证明抛物线平行于CD的弦的中点轨迹是RF，RF是抛物线的直径。由CD⊥RF可知RF是抛物线的对称轴。

另法：由ΔCPF与ΔPAF相似可得PF2=CF·AF；同理得：QF2=AF·DF。因此，CF=DF，再由∠RFC=∠RFD可知RF⊥CD，RF是对称轴。

性质 5 设抛物线上点A处切线与过抛物线的对称轴上点R处两切线分别交于P,Q，则FP=FQ,F是焦点。

性质 6 设抛物线上弦AB垂直于A处切线，T是A,B处切线的交点，F是焦点，过A垂直于AF的直线交TF于C。则有TF=FC,CB⊥TC。

证 如图6，由TA⊥AB,AF⊥AC可得∠TAF=∠BAC。由ΔATF,ΔTBF相似可得∠CTB=∠TAF=∠BAC，因此A,T,B,C共圆. 由TA⊥AB可得TC⊥CB.

性质 7 设T是抛物线上点A,B处切线的交点，F是焦点，过T的直径交AB于M交抛物线于S。则有：

(1)AM2=4FS·SM；

(2)如果焦点F在弦AB上， 则4SF=AB；

(3)设平行于TM的直线交抛物线于L交AB于N，则有AN·NB=4FS·LN。

图7过抛物线上两点切线交点的直径 图8焦点在弦上 图9平行抛物线的直径

证 (1)二次曲线的直径是平行弦中点的轨迹，抛物线的直径都平行。因此，TM平行于抛物线的对称轴。如图7，设S处切线交TA于E，有AM=MB，TS=SM，AM=2ES。由抛物线在点A处切线的光学性质及ΔAEF,ΔESF相似可知：∠ETS=∠FAT=∠FES，由点S处切线的光学性质可得∠EST=∠ESF。因此，ΔETS,ΔFES相似，ES2=TS·SF，即有AM2=4FS·SM。

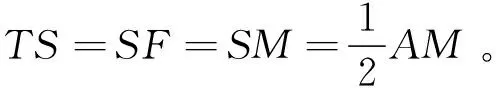
(3)LN与直径TM平行，LN也是抛物线的直径。如图9，设过L作AB的平行线交TM于R，LR的极点(即LR与抛物线交点处切线的交点)也在AM上，由 (1) 可得LR2=4FS·SR。因此

AN·NB=AM2-MN2=AM2-LR2=4FS·SM-4FS·SR=4FS·LN。

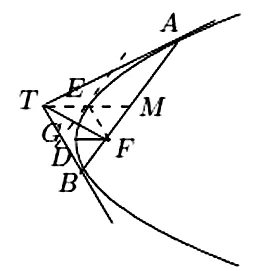
图10 焦点弦端点处切线

性质 8 设F,D分别是抛物线的焦点与顶点，T是焦点弦AB端点处切线的交点，则TF2=AF·FB=DF·AB。

证 如图10，T是焦点弦AB端点处切线的交点，TA⊥TB，而TF是直角ΔFAB底边上的垂线，TF2=AF·FB。设M是AB的中点，TM是共轭于弦AB的直径与对称轴DF平行。从抛物线切线的光学性质可得TM=AM。设E是TM与抛物线的交点，TE=EM。由于T在准线上，TE=EF，于是TF是∠DFE的平分线，E,D处切线的交点G也在TF上。由ΔEGF,ΔGDF相似 (性质2) 及EG,AB平行可得TG=GF，

TF2=4GF2=4EF·DF=AB·DF。

性质 9

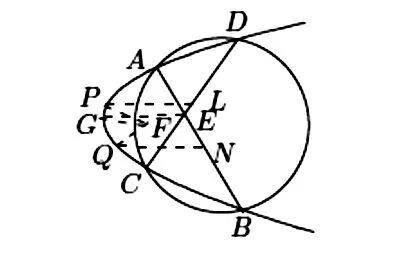
图11 圆与抛物线交于四点

(1)设圆与抛物线交于A,B,C,D四点，则AB,CD与抛物线对称轴的夹角相等；

(2)设圆与抛物线交于B,C，在A处相切，与抛物线的对称轴交于G及焦点F，则AC=BG，AB=CG。

证

(1)如图11，设AB,CD交于圆内点E，而QN,PL分别是共轭于抛物线弦AB,CD的直径 (分别是抛物线平行于AB,CD的弦的中点轨迹)，P,Q在抛物线上，N,L分别是AB,CD的中点，G是过E平行于抛物线对称轴的直线与抛物线的交点。由上面性质7有，AE·EB=4FQ·EG，CE·ED=4FP·EG。由A,B,C,D四点共圆，从AE·EB=CE·ED及前两式可得FP=FQ，因此点P,Q关于抛物线的轴对称，P,Q处的切线与轴的夹角相等。而抛物线在P,Q处的切线分别平行于CD,AB(见 [2] §4.2的讨论)[2]，这证明AB,CD与抛物线轴的夹角相等。由此可知，AC,BD与抛物线轴的夹角也相等。

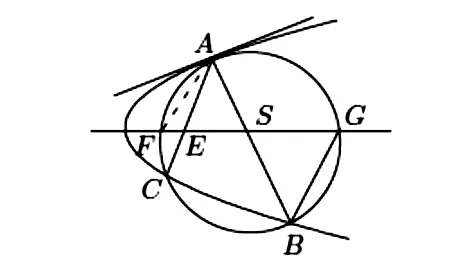
图12 圆与抛物线交于两点，切与一点

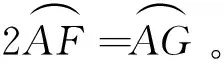
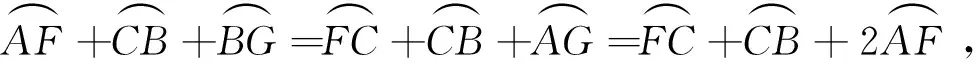
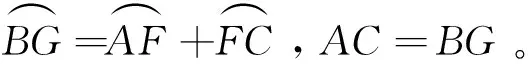
性质 10 设过焦点F作外切于抛物线的ΔABC的边BC的垂线，与ΔABC的外接圆交于另一点D。则有

(1)AD垂直于抛物线的对称轴；

(2)ΔABC的外接圆在焦点处切线与对称轴的夹角等于其三边与对称轴夹角的代数和。

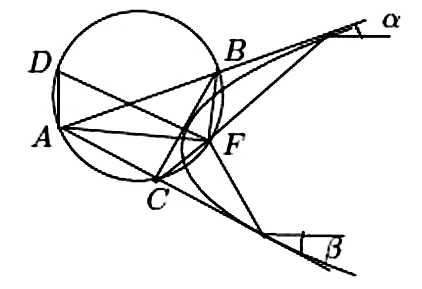
图13 过焦点作外切于抛物线的三角形

证 (1) 我们知道：抛物线的焦点F在ΔABC的外接圆上，DF⊥BC。如图13，设切线AB,AC与抛物线对称轴的夹角分别是α,β，假设αβ。由焦点的光学性质及性质2给出的许多相似三角形可得于是，

而直线AF与对称轴方向的夹角是β-α，这证明AD与对称轴垂直。因此过F垂直于AD的直线就是抛物线的对称轴。

(2)如图13，进一步设∠ABC=γ，∠ACB=τ，不难知道，α+β+γ+τ=π是ΔBCF的内角和. 三边AB,BC,CA与对称轴的有向角分别是：α,α+γ, -β，它们的和是2α+γ-β。外接圆在焦点F处的切线与AF的夹角是β+τ。由 (1) 可知圆在F处的切线与对称轴的夹角也是π-(β-α)-(β+τ)=2α+γ-β。

由 (1) 可以得到已知抛物线的一个外切三角形及对称轴的方向求作抛物线焦点的方法。

性质 11 设一族抛物线与两定直线相切，与其中一条切于定点。则这些抛物线的焦点在一个圆上，准线过定点。

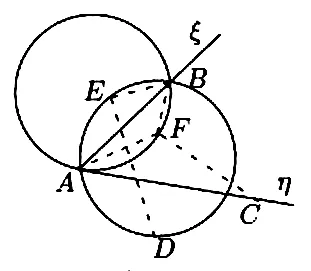
图14 一族抛物线与两定直线相切

证 如图14，设ξ,η是交于A的两直线，B是ξ上定点。设抛物线与直线ξ,η相切，切点分别是B,C，焦点F。这样的抛物线分别在直线ξ的两侧。由性质2, ∠AFB=π-∠BAF-∠ABF=π-∠BAC是定角。这证明与直线ξ,η相切，ξ上切点是B的抛物线的焦点在圆上，这个圆过点A,B与AC相切，它的弦AB上的圆周角等于直线ξ,η的两个夹角之一。

如图，再作一过A,B的圆使之与原来的圆关于ξ对称。取后一圆上点E使EB=BF，作EB的垂线交后一圆于D，则BD是此圆的直径，因此D是定点。EB,FB与ξ的夹角相等，由性质2的证明，ED是抛物线的准线。这证明了满足题中条件的抛物线的准线过定点D。

另一方面，任取前一圆上异于A,B的点F，有唯一的η上点C使∠AFC=∠AFB，这时ΔBAF,ΔACF相似。由性质3，有以F为焦点，与ξ,η分别切于B,C的抛物线。这些证明了性质。

2 应 用

以下是一些抛物线的问题[3-4]，有兴趣的读者可以试试。

1.已知抛物线上两点B,C处切线AB,AC。作此抛物线的焦点，准线，对称轴。

2.设抛物线上点A,B的切线交于C，F是焦点，过A,B,C的圆与CF交于另一点D。则有CF=FD。

3.设A是抛物线上点P,Q处切线的交点，∠APQ是直角，PQ交准线于T，则AT垂直于AQ。

4.设一族抛物线过两定点A,B，且都以A为顶点，则这些抛物线过B的切线与过A的切线与法线的交点分别在两个圆上。

5.设Y,Y′是抛物线的顶点D处切线上点，使得FY·FY′是常数，F是焦点，则抛物线过Y,Y′的切线的交点在一个圆上。