汽车纵梁数控平板冲孔机焊接床身动力学分析

李 敏，季翔宇，李志申

（1.山东建筑大学 机电工程学院，山东 济南 250100；2.济南铸造锻压机械研究所有限公司，山东 济南 250306）

现代冲孔成形工艺已不再依靠传统的钻削、激光等加工方法，而被工艺生产周期更短、效率更高的现代冲孔设备替代。作为现代冲孔的关键设备冲孔机，其加工精度高、定位准确，从而使冲孔机床在国内市场发展前景广阔[1]。

振动是工程实际中普遍存在的现象，也是力学中最重要的研究领域之一[2]。平板冲孔机在冲孔过程中发生振动，会影响加工质量和自身寿命，因此对平板冲孔机焊接床身进行动力学研究具有十分重要的意义。

1 有限元模型的建立

1.1 几何模型的建立

该汽车纵梁数控平板冲孔机焊接床身外形尺寸1430mm×1325mm×2455mm，其结构如图 1、2所示。

1.2 网格划分

为提高平板冲孔机焊接床身分析效率，导入前对该结构做如下简化[3]：①去除床身上的附件，如油缸、滑块、排料架、开关架等；②忽略床身上对应力几乎没有影响的工艺孔、线路孔及较小的螺栓孔等；③简化床身在加工制造时或安装其他附件所附带的倒圆角和过渡圆弧。

图1 平板冲孔焊接机床身三维几何模型

图2 平板冲孔机焊接机床身内部加强筋布置

将SolidWorks三维几何模型保存为Parasolid（*.x_t）[4]格式，通过 ANSYS 中的 File/Import/PARA 接口导入ANSYS中。焊接床身材料Q235，密度7850kg/m3，弹性模量2.1×1011Pa，泊松比0.3，选用20节点 Solid186单元[5]，分析采用5级精度，网格划分时考虑到贴板和侧板圆弧处和立板上的键槽处往往出现应力集中现象，在这2处网格划分细密一些，圆弧处网格尺寸为10mm，键槽处的网格密度为5mm，其余各板的网格尺寸为20mm。尺寸设置完成，先对面进行四边形自由网格划分，然后采用扫掠法[6]对整体划分网格，最终得到的有限元模型的单元数是219368，节点数725948。平板冲孔机床身有限元模型如图3所示。

图3 平板冲孔机床身有限元模型

2 模态分析

2.1 模态分析理论研究

模态固有频率和振型只与结构的刚度和质量分布有关。分析床身的固有频率和模态振型之间的关系，建立床身的振动微分方程如下[7]：

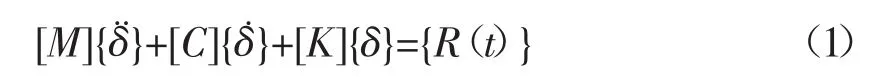
式中：R（t）——整体节点外载荷；

[M]——质量矩阵；

[K]——刚度矩阵；

[C]——阻尼矩阵；

模态分析属于线性分析[8]，在模态分析过程中，外载荷是随时间的变化而变化，结构阻尼也较小，因此不考虑外力和阻尼作用，即在 R（t）=0，C=0 时，得到无阻尼自由振动微分方程：

式中：ω——振动固有角频率。

结构自振过程中，行列式系数值为零，即｜K-ω2M｜=0，本文研究的平板冲孔机焊接床身模型有n个自由度，上式是关于ω2的n次方程，计算得到n个实根。ω1、ω2、ω3、ω4分别代表焊接床身的第一阶、第二阶...第n阶固有频率，然后将求出的特征值ω代入方程式（1），计算出相对应的特征矢量{δi}（i=1，2，3…，n），{δ1}、{δ2}、{δ3}…{δn}、即为焊接床身的第一阶、第二阶、…第n阶的固有振型[9]。

2.2 设置边界条件和求解

对焊接床身左右底板施加全约束；整体施加重力，以加速度的形式表示，大小是10m/s2，方向沿Y轴负方向。通过分块法[10]提取平板冲孔机焊接床身的前5阶固有频率，模态扩展数目也为5，选项设置时，不考虑集中质量矩阵和预应力，进行求解。

2.3 模态计算结果及分析

ANSYS计算得到前五阶固有频率，如表1所示列出了平板冲孔机焊接床身的前5阶固有频率，并通过扩展模态得到了各阶固有频率所对的振型图。

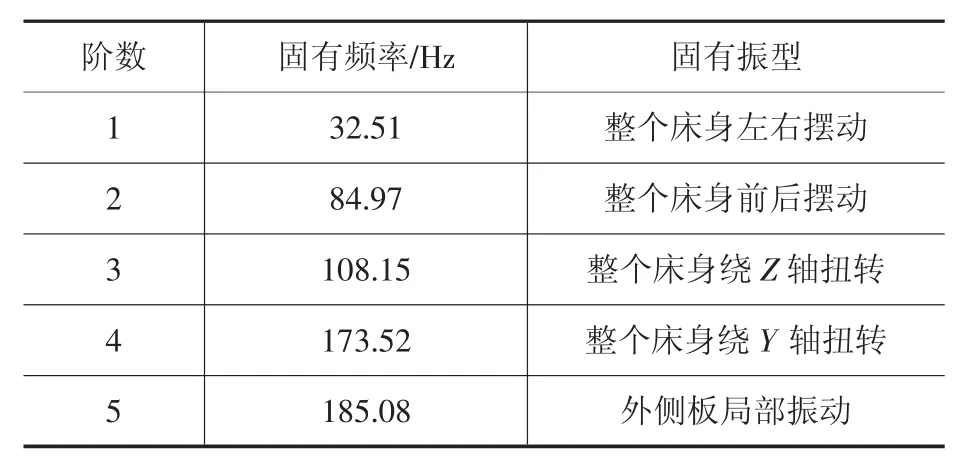
表1 平板冲孔机床身前5阶固有频率与固有振型

（1）第一阶模态频率值为32.51Hz，在该模态频率下，平板冲孔机焊接床身的振型属于弯曲振型，振型方向为整体左右摆动，如图4所示。最大位移出现在左右侧板的最上端，该振型会使底板左右侧应力较大，也会对地基与左右侧底板相连接的紧固螺栓产生较大影响。

（2）第二阶模态频率值为84.97Hz，在该模态频率下，平板冲孔机焊接床身的振型属于弯曲振型，振型方向为整体前后摆动，最大位移出现在立板的最上端，如图5所示。该振型会使焊接床身底板前后侧应力较大，也会对地基与前后侧底板相连接的紧固螺栓产生较大的影响。

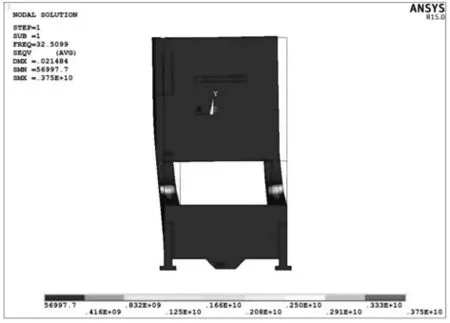
图4 平板冲孔机焊接床身第一阶振型图

图5 平板冲孔机焊接床身第二阶振型图

（3）第三阶模态频率值为108.15Hz，在该模态频率下，平板冲孔机焊接床身振型是绕Z轴方向扭转，如图6所示，最大位移出现左、右侧板的最上端，会使床身底部外侧承受较大的扭转应力，并对底板与地基连接螺栓产生较大作用。

图6 平板冲孔机焊接床身第三阶振型图

（4）第四阶频率值为173.52Hz，在该模态频率下，平板冲孔机焊接床身振型是绕Y轴方向扭转，如图7所示，最大位移出现左、右侧板的最上端，会使床身底部内侧承受较大的扭转应力，并对地基连接螺栓产生较大作用。

（5）第五阶模态频率值为185.08Hz，如图8所示，在该模态频率下，平板冲孔机焊接床身最大位移出现在外侧板上，外侧板产生局部振动。

3 谐响应分析

3.1 谐响应分析理论研究

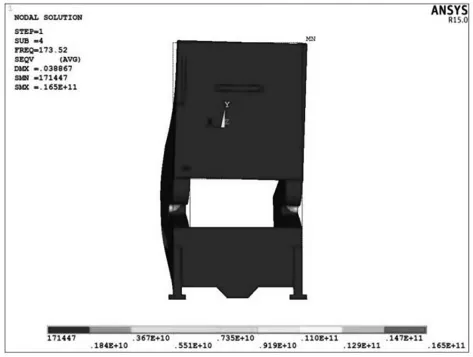
图7 平板冲孔机焊接床身第四阶振型图

图8 平板冲孔机焊接床身第五阶振型图

在简谐激励作用下，系统的动力学响应由两部分构成，其中包括由初始条件决定的瞬态衰减自由振动和由简谐激励决定的稳态受迫振动。谐响应分析只计算稳态受迫振动。受迫振动通用运动方程为[11]：

式中：M——结构的质量矩阵；

C——结构的阻尼矩阵；

K——结构的刚度矩阵；

F（t）——激振力向量。

假定作用在多自由度系统上的各简谐激励的频率和相位相同，则激振力可用复数表示为：

式中：F（t）——激振力的幅值；

ω——简谐激振频率；

F1——结构的实激振力向量；

F2——结构的虚激振力向量。

位移可表示为

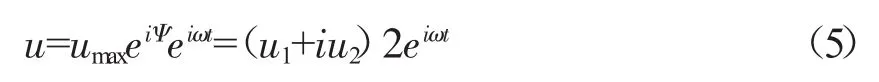
式中：umax——位移幅值

u1——实位移矢量；

u2——虚位移矢量。

谐响应分析的运动方程为：

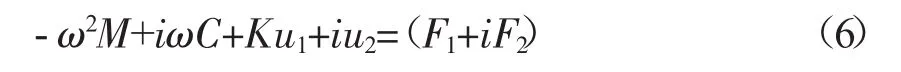
3.2 谐响应加载和求解

简谐激振力以实部和虚部[12]形式输入，激振力的点分别选在立板平键上表面中心节点上，方向向上，另一激振力作用在内外侧板中心轴线节点上，方向向下。作用在平键上的力幅值为F1=1.2×106N，内外侧板上的力F2=0.6×106N，虚部均为为0，对焊接床身底板所有自由度施加全约束。由模态分析得出的对焊接床身影响较大的前5阶频率在0～200Hz范围内，因此这里选择的激励频率范围0～200Hz，载荷子步为50，采用阶梯加载方式，用完全法[13]进行求解，选用幅值+相位角作为输出选项。加载模型如图9所示。

图9 谐响应分析模型

3.3 求解结果分析

求解结束，通过时间历程后处理器查看结果，为了绘制位移-频率关系曲线需要定义变量，焊接床身立板上的平键、侧板和贴板圆弧、左侧板应力比较大，因此选取焊接床身平键、侧板和贴板圆弧处、左侧板上的最大应力值点为关键点，分别为548257号、174715号、166489号，用 A、B、C 表示；定义每个节点在X、Y、Z三个自由度方向的位移，绘制的位移-频率响应曲线如图10～13所示。

图中的峰值点为共振现象发生的位置，所对应的频率为模态分析所得的平板冲孔机焊接床身的固有频率，从图10～13幅值曲线图不难看出，平键、侧板和贴板圆弧、左侧板、内外侧板左端点、内外侧板中间点、内外侧板右端点X、Y、Z三个方向的峰值对应频率在84.97Hz附近，即第二阶固有频率，可以推出激振频率出现在80～85Hz时，床身会出现共振现象，为避免对床身产生不必要的破坏，工作频率不要接近第二阶固有频率。左侧板的位移幅值最大，外侧板右端点位移幅值最小；关键点处Z方向的位移大于Y方向的位移，Y方向的位移大于X方向的位移。这与实际工作情形相吻合。

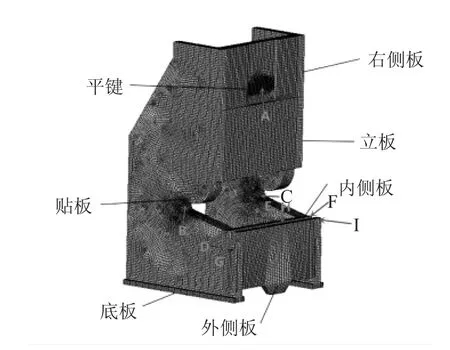
图10 焊接床身所选关键点位置示意图

图11 平键最大应力点A的幅值响应曲线

图12 侧板和贴板圆弧处最大应力点B的幅值响应曲线

图13 左侧板最大应力点C的幅值响应曲线

4 结论

通过对平板冲孔机焊接床身进行模态分析，得出了前5阶的固有频率和与之相对应的振型，确定了谐响应频率分析范围0～200Hz，然后对平板冲孔机焊接床身进行了谐响应分析，考察了重要位置在所选频率范围内的响应情况，得出了固有频率的位移响应幅值曲线，确定了84.97Hz是对焊接床身动态特性影响最大的固有频率。