基于极限学习机的高品质葡萄酒等级识别模型

韩方凯，张雪柯，吕日琴，张东京，翟科峰

1.宿州学院生物与食品工程学院，宿州，234000；2.江苏大学食品与生物工程学院，镇江，212013

1 相关研究与问题提出

葡萄酒色味俱佳、品位高雅，且具有重要的保健功效，在全球范围内广受欢迎。近年来，我国葡萄酒消费量快速增加，2016年为17.2亿升，较2015年增长6.9%，增幅位居全球首位。与此同时，葡萄酒的品质问题也愈来愈受到消费者和政府的关注。目前，市场上葡萄酒品牌多样，品种繁多，各档次产品玲琅满目，价格参差不齐，更甚者出现采用人工色素和酒精溶液勾兑的假酒[1]。价格虚高会造成消费者的经济损失，假冒伪劣的葡萄酒则会直接影响到消费者的身体健康，甚至危及生命安全，因此保障葡萄酒产品的优良品质具有重要的现实意义。作为品质控制重要的一环，葡萄酒品质的快速、客观、准确评价非常重要。

传统的葡萄酒品质检测方法主要有理化指标测定法和感官评价法。葡萄酒品质的理化指标测定法是指通过检测葡萄酒部分理化指标值来对葡萄酒进行品质评定，如品质优良的葡萄酒酒精度不应低于7.0%vol、干浸出物不应低于16.0 g/L、挥发性酸不应高于1.2 g/L、甲醇不应高于400 mg/L，且应具有较高的酚类物质含量等。理化指标检测法的重要缺陷在于，难以实现葡萄酒品质的综合评价。实际操作中，葡萄酒综合品质的评价方法主要通过感官分析进行。葡萄酒品质的感官分析指评价员用口、眼、鼻等人体感觉器官对葡萄酒产品的感官特性进行检查与分析评定。国家标准GB 15037-2006《葡萄酒》对葡萄酒的色泽、澄清度、香气、滋味等感官特性提出了明确的要求，并据此将成品葡萄酒按品质等级分为五类，即优质品、优良品、合格品、不合格品和劣质品，而推荐性国家标准GB/T 15038-2006《葡萄酒、果酒通用分析方法》则提供了葡萄酒感官品质的详细分析方法，用以指导实际操作。感官评价实用性较强，然而培训感官评审专家是一个复杂的过程，成本较高。理化成分是感官评审结果的物质基础，两者存在重要的相关关系。建立基于理化指标的葡萄酒感官评审结果预测模型，以快速评价葡萄酒的综合品质，具有重要的研究意义。2009年，Paulo Cortez等人以葡萄酒理化指标数据作为输入、感官评审结果作为输出，构建支持向量机(Support Vector Machine,SVM)预测模型。结果显示，SVM模型的预测准确率优于多元回归和神经网络预测模型[2]。2010年，王金甲等人提出了一种基于线性判别分析的可视化方法评价葡萄酒质量，建立葡萄酒理化指标与感官分析结果之间的关系。结果显示，所开发的排序分类器的预测性能优于SVM和神经网络，平均误差率为88.4%，且效率最高，耗时为1 238 s[3]。

极限学习机(Extreme Learning Machine,ELM)是一种针对单隐含层神经网络(Single-hidden Layer Feedforward Neural Network,SLFN)的新型算法，由南洋理工大学黄广斌教授等人于2006年首次提出[4]。与传统的训练方法相比，ELM随机产生输入层与隐含层的连接权值及隐含层神经元阈值，建模过程中只需设置隐含层神经元个数，模型便可以获得唯一最优解，具有学习速度快，泛化性能好等优点，现已广泛用于模式识别领域。大量研究表明[5-7]，ELM较传统的神经网络算法可显著提高运算速度。然而，国内外尚未出现ELM算法在葡萄酒品质分析中的应用。本研究尝试采用ELM算法，考察葡萄酒理化指标与感官评审结果的相关关系，构建高品质葡萄酒等级的快速识别模型。

2 材料与方法

2.1 数据来源

研究所用葡萄酒理化指标与感官评审结果数据均来自于葡萄牙绿酒区域葡萄栽培委员会(Commission of Viticulture of the Vinho Verde Region,CVVVR)[2]。理化指标包括固定酸(酒石酸)、挥发酸(乙酸)、柠檬酸、残糖、氯(氯化钠)、游离二氧化硫、总二氧化硫、密度、pH值、硫酸盐(硫酸钾)和酒精度共11个。感官评审结果将受试样本划分为0～10个等级，等级0表示品质极差，等级10表示品质极好。研究将高品质葡萄酒等级定义在6～8等级范围内，共包含855个样品，用于ELM快速预测模型的构建。

2.2 ELM建模方法

ELM是针对SLFN的新算法，假设输入层有n个神经元，即对应n个输入变量；隐含层有l个神经元；输出层有m个神经元。本研究中，n=1～11，m=1。设输入层与输出层的连接权值为w(l×n)，wji表示第i个神经元与隐含层第j个神经元间的连接权值；隐含层与输出层连接权值β(l×1)，βj表示隐含层第j个神经元与输出层之间的连接权值；隐含层神经元阈值b(l×1)；具有Q个样本的训练集输入矩阵x和输出矩阵y如下:

设隐含层神经元的激活函数为g(x)，则网络的输出T为:

T=[t1,t2,…，tQ]1×Q

其中，wi=[wi1,wi2,…,win]，xj=[x1j,x2j,…，xnj]T；亦可表示为Hβ=TT,其中：

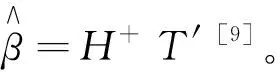
3 结果分析与讨论

3.1 葡萄酒理化信息的主成分提取

由建模数据采用的理化指标可以看出，受试葡萄酒样本的11个理化指标值之间存在一定的共线性。多重共线性的变量无疑存在重叠信息，对模型的运算速度会产生一定影响。主成分分析(Principal Component Analysis，PCA)可通过正交变换将多变量之间的共线性去除，同时起到降维作用[10]。经PCA分析，主成分的累积贡献率如图1所示，可看出前三个主成分的累计贡献率可达99.64%，前三主成分得分已能代表原始变量大部分的信息。

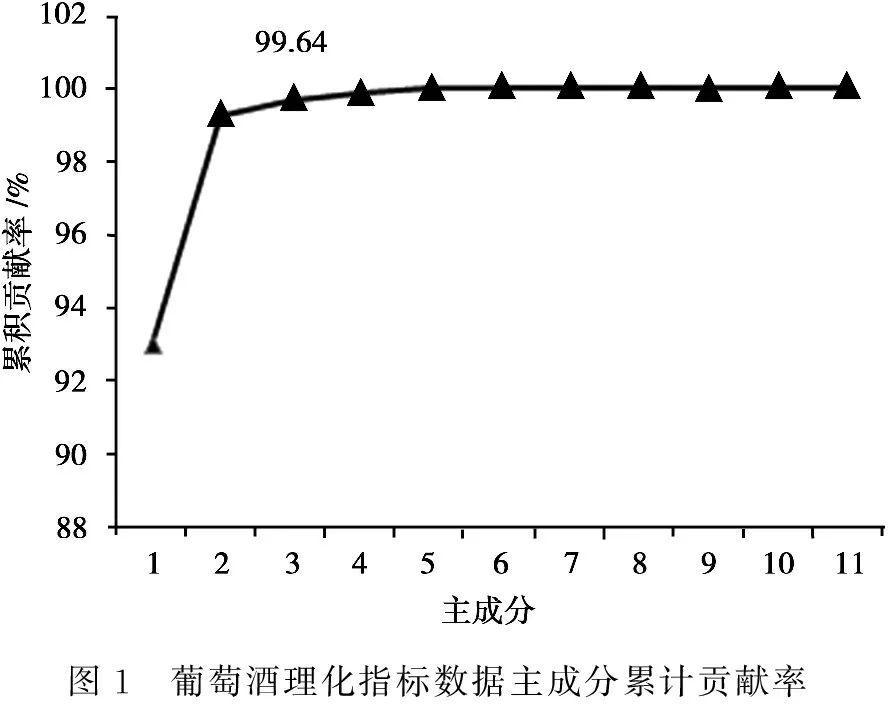
图1 葡萄酒理化指标数据主成分累计贡献率

葡萄酒理化指标前三个主成分的载荷如表1所示。可以看出，对第一主成分和第二主成分影响较大的变量为样本中二氧化硫残留；对第三成分影响较大的变量为固定酸和残糖。受试葡萄酒样本在前三个主成分中的空间分布如图2所示，可看出样本点分布重叠严重，仅仅靠线性判别方法难以实现高品质葡萄酒样本的准确识别。

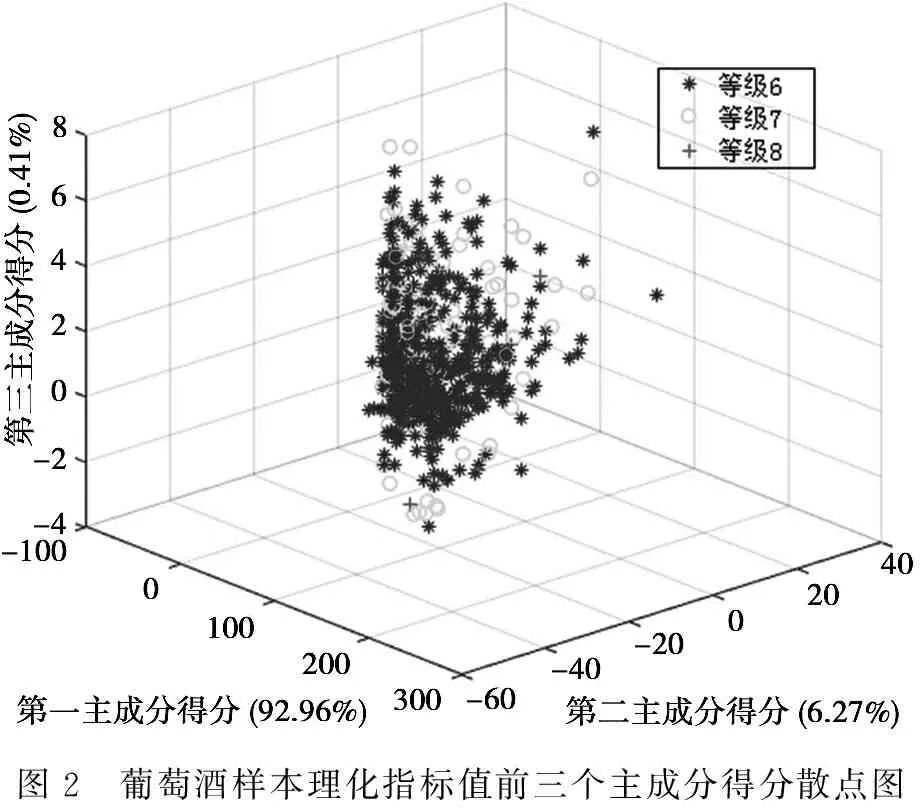
图2 葡萄酒样本理化指标值前三个主成分得分散点图

3.2 高品质葡萄酒等级的ELM分类分析

由PCA分析结果可知，葡萄酒理化指标数据的前三个主成分已可代表原始变量大部分的信息。因此，研究采用葡萄酒样本的前三个主成分得分作为ELM的输入，以葡萄酒样本的品质等级作为网络的输出，随机选取样本总数的2/3为训练集，另外1/3为测试集，构建ELM预测模型。经过多次比较，选用hardlim函数作为ELM输出层传递函数。在ELM模型的构建过程中，考察了不同隐含层神经元个数对模型预测性能的影响，当隐含层神经元个数为151时，训练集预测的准确率为82.46%，测试集预测准确率为80.7%，达到较好效果。且整个建模与预测过程用时不足1 s，效率极高。

4 结 论

葡萄酒品质的准确、快速检测对保障葡萄酒品质具有重要的作用。研究以葡萄酒理化指标值作为输入，葡萄酒感官评审结果作为输出，构建ELM定性识别模型。由实验结果可知，当ELM隐含层神经元个数为151时，模型的预测性能最好，独立样本的正确识别率可达80%以上，且效率极高，运算用时不足1 s。可见，所建ELM模型可用于高品质葡萄酒等级的快速预测。

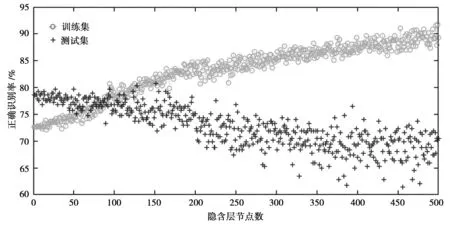
图3 不同隐含层神经元个数下ELM模型训练集和测试集正确识别率