基于ABAQUS的扭动摩擦有限元数值模拟研究
曹 波,高 尚,张雅晶,董文彬,张春雨,姚智华
安徽科技学院机械工程学院,凤阳,233100
扭动摩擦普遍发生在许多工程中,它是导致人体髋关节、膝关节以及轴承、电力、汽车挂车的转向回转盘和火车转向架失效的主要原因[1]。目前大多数学者研究扭动摩擦是在恒定载荷作用下的扭动,研究者针对扭动摩擦展开了大量的实验研究,揭示了扭动摩擦磨损的机理及其规律[2-5],并建立扭动模型,对扭动实验过程中出现的现象给予合理的解释。伍灿[6]对铝合金扭动微动磨损实验研究表明,摩擦扭矩-角位移幅值曲线随着循环次数的增加有规律地发生变化,部分滑移区的摩擦扭矩值持续较低,混合滑移区以及完全滑移区的摩擦扭矩值呈一定规律变化。刘娟研究扭动微动摩擦力数值分析,发现界面摩擦应力对表面材料损失起着至关重要的作用,不同滑移区摩擦应力分布不同,导致磨损机理各不相同[7]。王世博通过实验研究和仿真模拟研究发现,接触界面主要分为三个区域,磨损最严重的区域在中间混合区域,实验结果与仿真结果相吻合[8-9]。然而,在许多工程中扭动摩擦并不是在恒定载荷作用下发生的,而是在交变载荷作用下发生磨损,如火车在运行过程中,火车心盘承受着交变的动载荷,心盘磨损到一定程度,则影响火车的运行安全,但至今学界对交变载荷下的扭动摩擦研究较少,因此,本文运用ABAQUS仿真软件模拟交变载荷下的扭动摩擦,以期得到交变载荷下扭动运动应力变化规律。
1 接触理论
接触力学是研究摩擦学的最基理论,Hertz在接触理论基础上建立在恒定静载荷作用下的接触模型[10]:
(1)
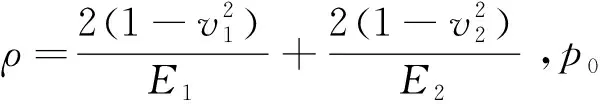
在接触表面施加交变法向载荷,即上试样45钢对下试样铸型尼龙复合材料进行冲压,假设接触面的加载圆法向位移均匀,则接触界面承受的法向应力分布为[11-12]:
(2)
式中:r表示半径;a表示接触区域的半径;pz表示半径为r的圆环产生的压强,对法向应力分布公式(2)进行积分,可得法向应力:
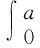
(3)
由公式(3)可得:
(4)
将公式(4)代入公式(2),得:
(5)
2 有限元模型
2.1 有限元模型建立、赋予材料属性
采用ABAQUS有限元仿真软件建立三维模型,如图1(a)所示。上试样材料选取45钢,下试样材料选取铸型尼龙复合材料, 45钢尺寸为的Ф20 mm×8 mm,与之接触的下试样铸型尼龙复合材料尺寸为Ф40 mm×6 mm。由于45钢的杨氏模量比铸型尼龙复合材料的杨氏模量高,同时由于铸型尼龙复合材料是磨损面,因而铸型尼龙复合材料作为次平面,45钢选为主平面,建立主控—次属的面面接触扭动模型,在主平面几何中心建立参考点(RP),便于对主平面施加约束与边界条件。根据表1所示的材料特性,在property模块中分别定义45钢与铸型尼龙复合材料,并将其分别赋予主平面与次平面。

表1 材料特性
2.2 施加边界条件、载荷与网格划分
对主平面和次平面采用扫掠的方式划分网格,次平面网格最大尺寸为1.5 mm,为了观察接触区域的应力变化情况,对次平面与主平面接触的区域做进一步网格细化,如图1(b)所示,接触区域最大尺寸为0.5 mm。对铸型尼龙复合材料底面的水平位移、竖直位移和转动位移进行约束,对45钢的参考点(RP)Z方向自由度进行约束,约束其扭动角度为10°,通过参考点(RP)对45钢施加周期性法向的正弦载荷,法向平均载荷为400 N,载荷频率为2 Hz。载荷加载方式按照公式F=400+Asin(4πt),A表示载荷振幅,载荷振幅分别为30 N、60 N、90 N。各振幅下扭动仿真时间均为2 s,仿真步长为0.025 s。
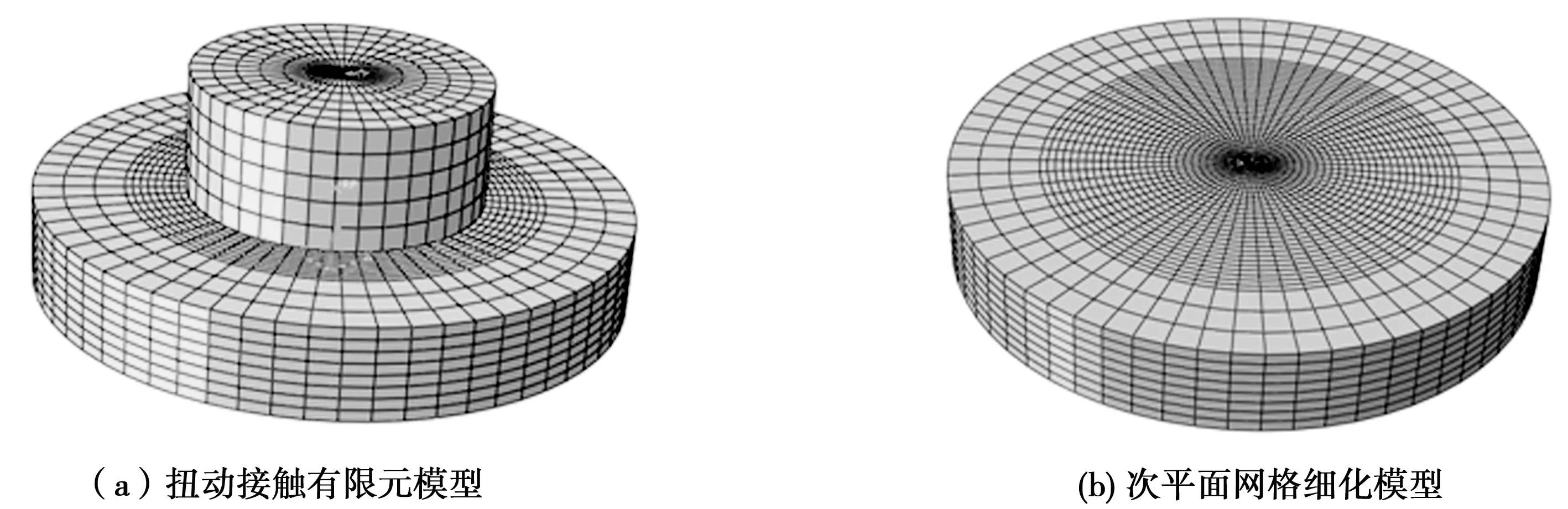
图1 扭动模型接触模型
为了研究交变载荷下扭动摩擦过程中接触面的应力变化规律,在接触区域内每隔2 mm取一个点,沿着接触半径的方向依次均匀取A、B、C、D、E、F六个点,其中,A点为接触正中心的位置,F点为接触边缘点,如图2所示。
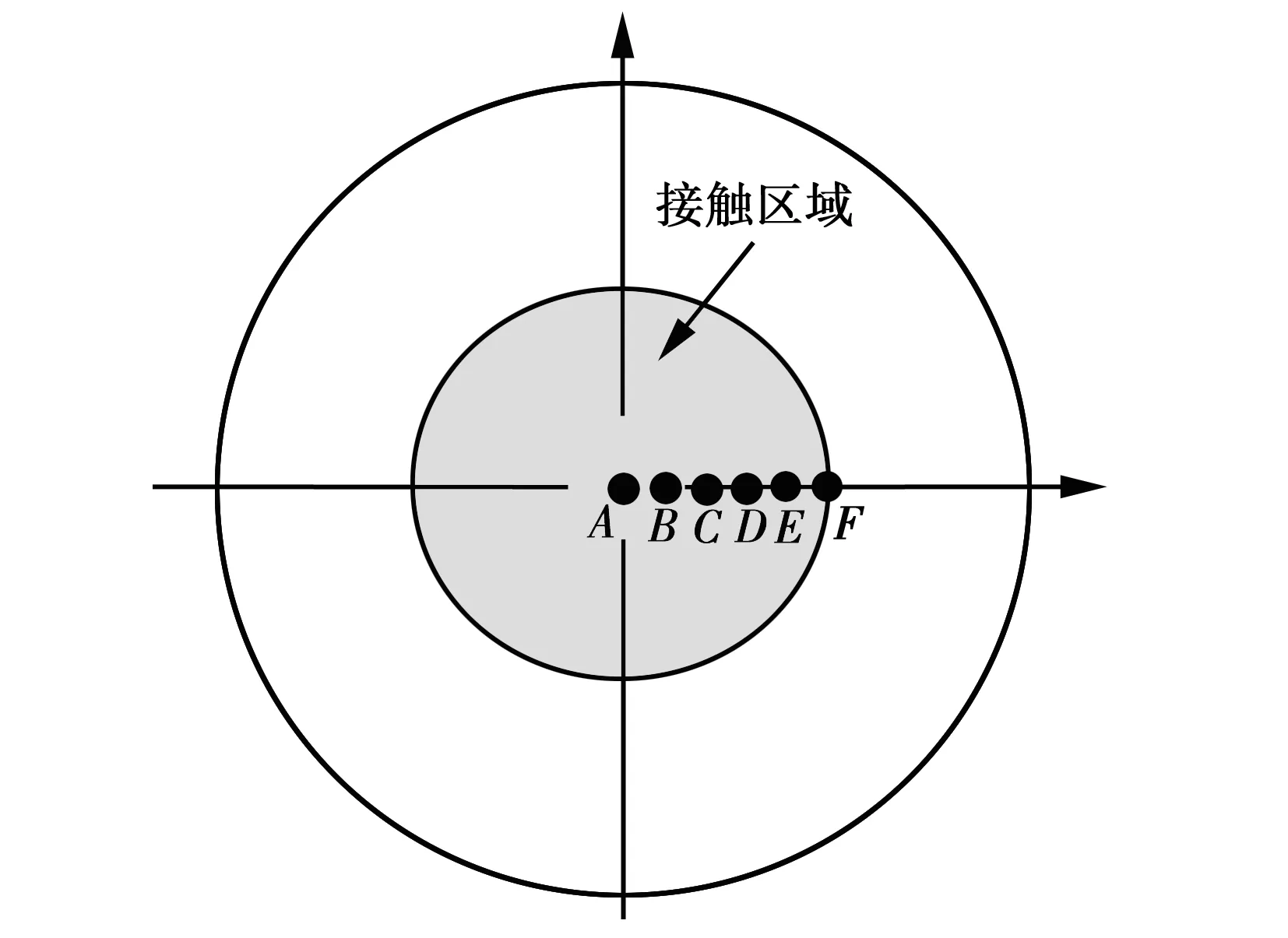
图2 接触区域内沿着半径方向取点示意图
3 结果分析
图3为接触区域内不同接触点等效应力随时间变化曲线。在接触正中心位置A点时,等效应力呈现出明显的周期性变化,载荷振幅越大等效应力的振幅越大,随着时间的变化,等效应力周期性并未被破坏,这主要是由于在接触正中心切向位移为零所致。距离接触中心2 mm时,即距离接触中心2 mm,在一个载荷周期之后,等效应力呈现不同程度的波动,载荷振幅越大,等效应力在峰值时波动越明显,等效应力大于平均值时,均表现出较大的波动,等效应力小于平均值,表现出良好的周期性变化。距离接触越远,等效应力波动程度越大,接触半径在8 mm以内,等效应力小于平均值时均表现出周期性变化的规律,等效应力大于平均值时呈波动状态。接触半径大于8 mm时,等效应力在任何时刻均呈现剧烈的波动,载荷振幅越大,波动越剧烈。
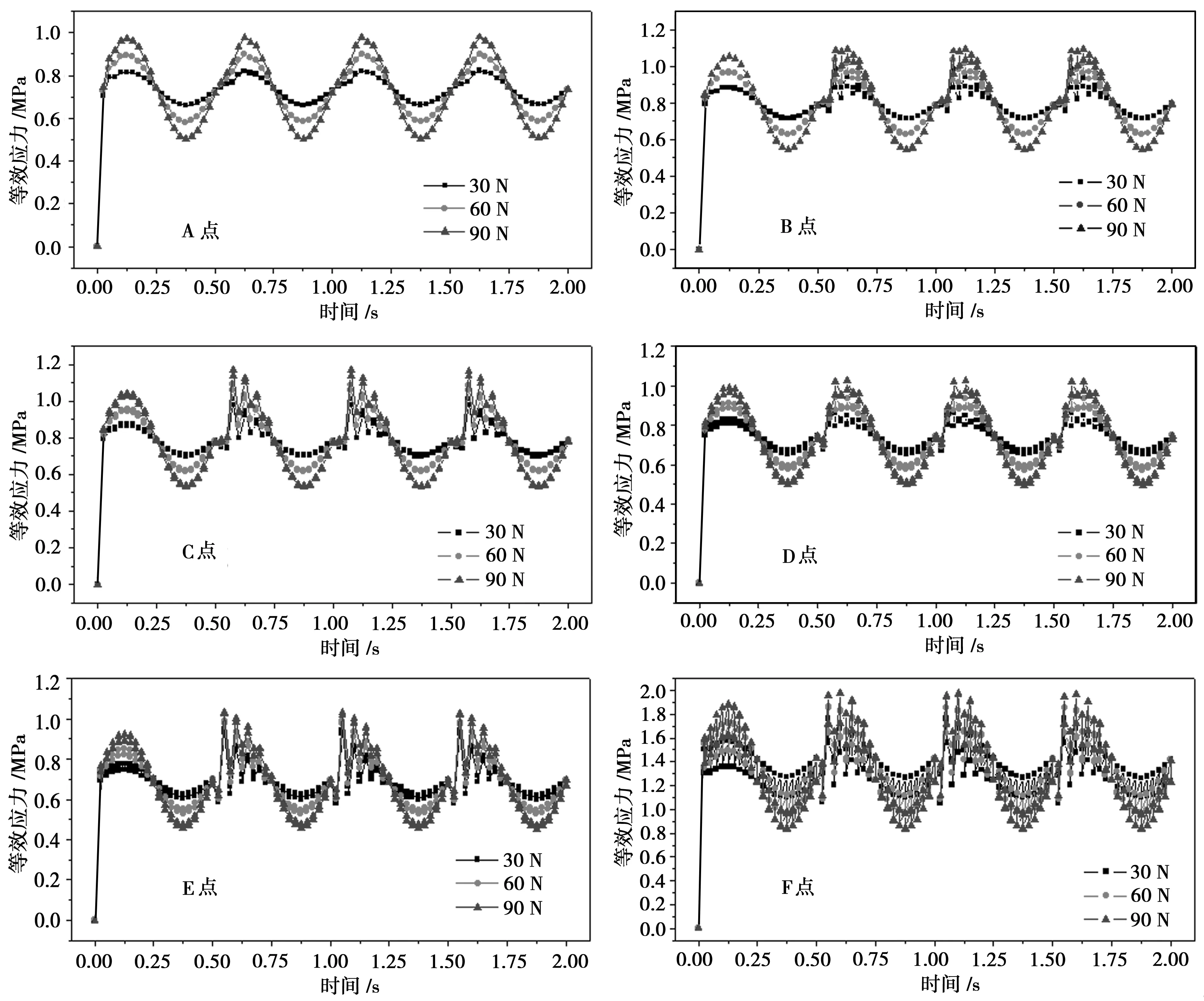
图3 沿着半径方向各点的等效应力变化曲线
图4为不同载荷振幅下等效应力变化趋势。在各工况下,除中心点A,表现出的周期性与设定的周期相吻合,接触半径在0~8 mm范围内,等效应力缓慢变化。在接触边缘区域,呈现震荡变化,说明在接触边缘区域磨损严重,接触边缘区域最大等效应力出现在0.625 s,最小等效应力出现在1.375 s,因此分别提取各工况下0.625 s和1.375 s时刻等效应力断面作应力分布图。
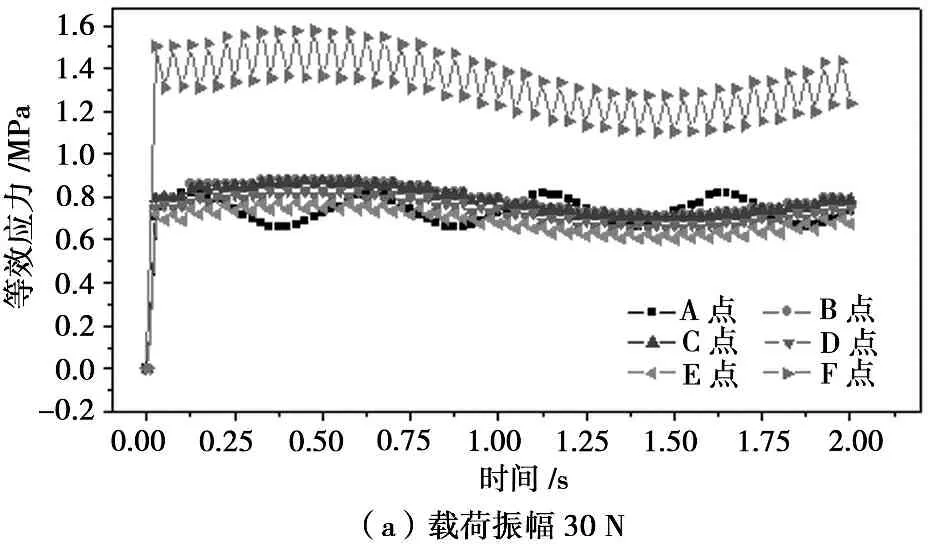
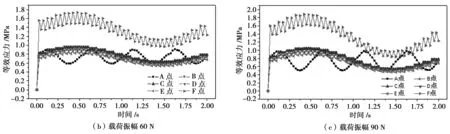
图4 不同载荷振幅下等效应力应力变化曲线
如图5所示,两种时刻下,等效应力均关于中心点呈对称分布。t=0.625 s,等效应力在断面的分布相类似,最大等效应力随载荷振幅增加而增大,在中间接触区域并未出现最大等效应力,但是中间区域的等效应力随着载荷增大依然呈增加的趋势。最大等效应力沿着竖直方向分布的深度大约为2 mm,载荷振幅的增加对应力的分布影响较小,但是对应力数值的影响较大,这也就说铸型尼龙复合材料在扭动过程中,接触中间区域表层破坏程度(0~8 mm)小于边缘区域(8~10 mm)的破坏程度(亚表面层的基体容易被破坏)。当时间t=1.375 s,等效应力应力分布与0.625 s时应力分布相类似,但是最大等效应力随振幅的增加而减小,主要是此时接触界面承受的法向载荷最小;虽然此时对铸型尼龙基体的破坏程度减小,但是在交变应力作用下,接触边缘区域容易萌生裂纹,将造成更严重的破坏,载荷振幅越大这种破坏越严重。
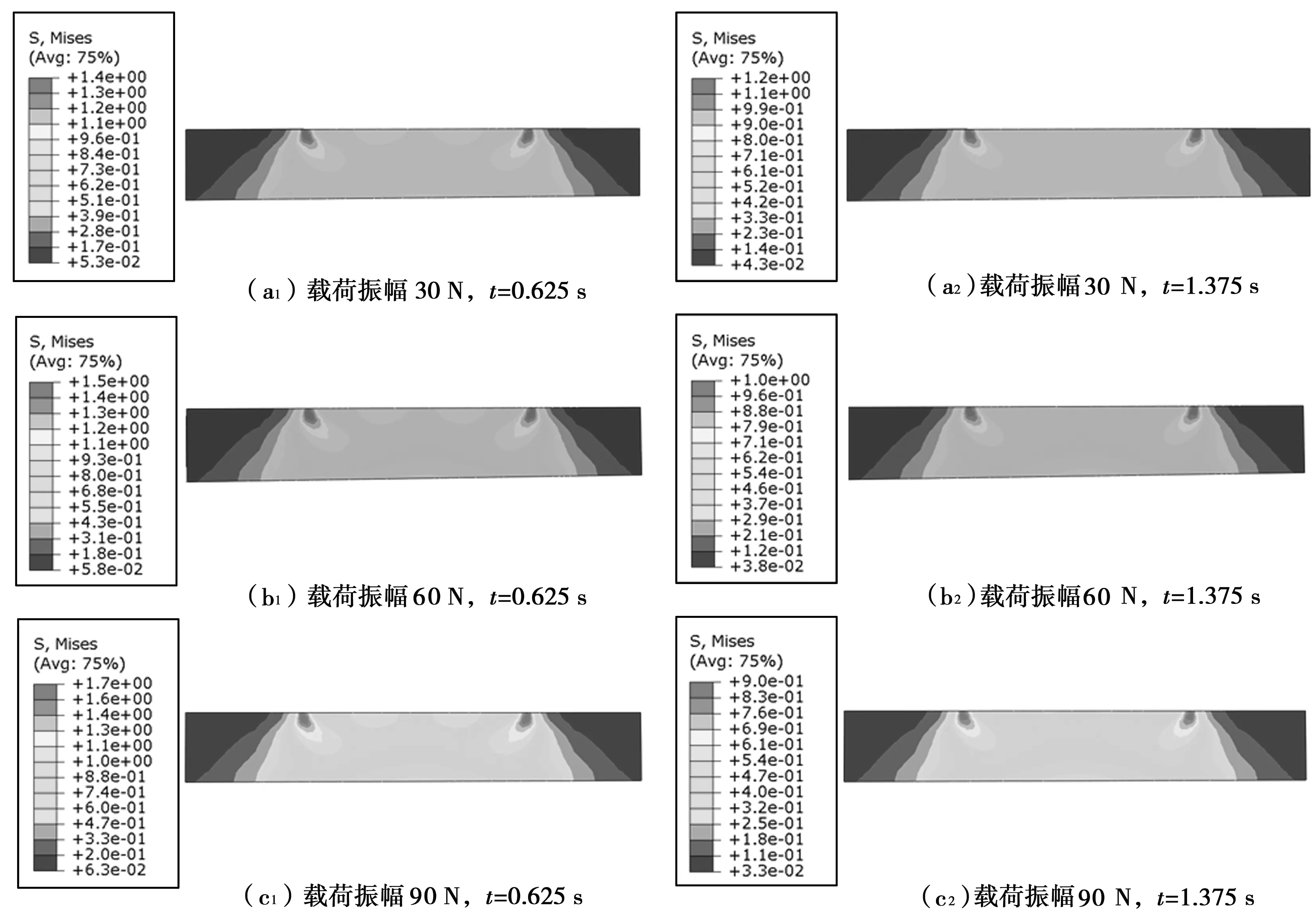
图5 等效应力云图断面分布情况
图6为接触应力在一个载荷周期内的变化曲线。接触应力曲线呈“浴盆状”,接触应力在接触边缘区域最大,在中间接触区域0~8 mm之间,接触应力变化平稳,8~10 mm之间呈线性增加,在0.125 s时,接触应力最大。从图7中可以看到,在三种不同载荷振幅下,接触应力分布相似,在接触边缘区域都存在最大应环,但接触应力的最大值不同,最大接触应力随着载荷振幅的增加而增大,分别为2.7 MPa、 2.95 MPa、3.21 MPa,这是由于在较高的载振幅作用下,边缘区域的应力环的变形较大,导致接触应力较高,这是导致在扭动过程中接触边缘区域容易磨损破坏的原因。
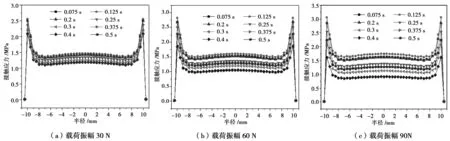
图6 接触应力沿着半径方向在不同时刻的变化曲线

图7 不同载荷振幅下接触应力云图
4 结 论
根据以上分析和仿真模拟,本文得到以下认识:
(1)在接触正中心,等效应力呈现周期性变化;当接触半径大于8 mm,等效应力呈波动状态,而且载荷振幅越大,波动越剧烈。
(2)当接触半径小于8 mm时,等效应力和接触应力变化较平缓,最大接触应力随载荷振幅增大呈上升趋势,说明载荷振幅对等效应力和接触应力的应力分布影响较小。
(3)在接触边缘8~10 mm之间,等效应力和接触应力均出现最大应力环,且接触应力沿着半径方向呈线性增加,最大等效应力沿着竖直方向的分布深度大约为2 mm,表明载荷振幅对接触边缘区域应力影响较大,边缘区域磨损较严重。

