一种基于EMD和典型谱峭图的改进型共振解调方法

刘文朋，刘永强，杨绍普，廖英英

(石家庄铁道大学a.机械工程学院；b.土木工程学院，石家庄 050043)

滚动轴承在含局部损伤故障运转时将会产生冲击尖脉冲信号，将含有故障信息的冲击信号提取出来是滚动轴承故障诊断的关键[1]，但机械设备运转时产生的大量振动噪声给故障冲击信号的检测造成了很大困难[2]。共振解调法是利用共振将尖脉冲信号输出为频率与传感器固有频率相接近的减幅振荡信号，从而放大了故障信息，再采用带通滤波器将故障冲击信息与低频干扰信息分离，包络分析提取出包含故障特征信息的低频波形，最后通过频谱分析观察是否含有故障的特征频率，从而判断故障发生的位置[3]。

然而，传统共振解调中带通滤波器参数的选择通常取决于历史数据和具体使用者的经验，常需要进行大量的尝试，无法适应轴承应用环境的变化和多样性。谱峭度方法对含有冲击信息的信号十分敏感，可以通过比较各个频带上的峭度值从而精确定位谱峭度值最大时所在的频带[4-6]。文献[7-9]重新定义了谱峭度并提出了快速谱峭图的算法，但其采用频带交替二分和三分法进行分解，所求得的频带往往过大[10]。典型谱峭图算法可以针对性地自动选择滤波带宽和中心频率，弥补了快速谱峭图带宽过大的问题[11],但当振动信号信噪比较低，噪声干扰较大时，效果也不太理想。

因此，为提高特征提取的准确性，提出一种基于EMD和典型谱峭图的改进型共振解调方法，首先对振动信号进行EMD分解，根据相关系数和峭度准则选取最优IMF分量重构信号，再利用典型谱峭图选取最佳带通滤波器参数进行带通滤波，最后进行包络解调和故障识别。

1 EMD降噪理论

EMD本质上是将一个时间序列信号进行平稳化处理，其结果是将一段复杂的信号分解成为具有不同尺度的固有模态分量(IMF)，然后选取某些IMF进行重构信号，起到滤波降噪的作用。

为尽可能抑制噪声信号，突出共振冲击信号，结合已有研究成果及轴承故障信号的冲击特征，选择同时运用相关系数和峭度准则进行最优IMF分量的选取，进而重构信号，达到降噪的目的。

1.1 相关系数

相关系数用于评估变量之间相关程度的大小，其定义为

(1)

式中:Cov(X,Y)为变量X与Y的协方差；D(X)，D(Y)分别为变量X与Y的方差。2个变量之间的相关系数越大，两者的相关性也越大。

1.2 峭度准则

峭度是一个量纲一的参数，用于描述信号的波形尖峰度程度，其定义为

(2)

式中：E为变量的期望；μ为信号X的均值；σ为标准差。轴承表面存在损伤时，其振动信号中会出现冲击成分，峭度值便会超过3，而且故障越明显，峭度值越大[13]。因此，可以将峭度值大于3作为一种选取敏感IMF分量的准则，选取保留原信号更多冲击成分的IMF分量。

2 典型谱峭图算法

2.1 谱峭度

谱峭度定义为能量归一化的4阶谱累计量，可以通过度量一个信号在每根谱线的峭度值，从而确定具有明显冲击成分信号所在的频段。其定义为

(3)

式中：|·|和〈·〉分别表示取模和数学期望；H(t,f)为振动信号x(t)在频率f处的复包络。

谱峭度的大小与所选的共振频带有关，进行故障特征提取的前提就是寻找使谱峭度最大的中心频率和带宽。

2.2 典型谱峭图算法

由于滚动轴承的故障表现为以通过频率为调制频率的幅值调制现象，典型谱峭图依据频谱中存在3次谐波时对应的峭度值最大原则[12]选择故障频率的3倍特征频率为带宽，这样可以保证得到的滤波器一旦包含有故障冲击成分时至少有3条调制谱线，同时也尽可能避免了噪声频率成分的干扰。

区间划分方法如图1所示，图中：fs表示采样频率；f表示故障频率。第1个区间为0～3f，中心频率为1.5f；第2个区间为1f～4f，中心频率为2.5f。以此类推，区间重叠。

图1 区间划分

典型谱峭图的流程如图2所示。以特征频率为迭代步长对振动信号的频谱区间进行划分，计算每个区间的峭度并绘制谱峭度曲线，然后找出谱峭度曲线上最大值对应的频率作为中心频率。与快速谱峭度相比，该方法有效避免了频带区域过宽或过窄的问题；但当信号中噪声比较强时，特别是含有较强脉冲信号干扰时，有效性大大降低，找到的最大谱峭度频带往往不是最佳的共振频带。

图2 典型谱峭图的流程

3 改进型共振解调方法

将EMD和典型谱峭图算法结合到共振解调方法中，形成了一种改进型共振解调方法。首先，对采集的振动信号进行EMD分解，得到一组IMF分量；然后，通过相关系数和峭度准则选取最优的IMF分量，重构信号并进行典型谱峭度图算法分析，选取取得最大谱峭度时对应的带宽和中心频率；最后，将最优参数输入到带通滤波器中，对经过带通滤波后得到的高频共振成分进行包络解调和故障识别。具体的流程如图3所示。

图3 改进算法流程图

4 试验验证

为验证上述方法在滚动轴承故障特征提取中的有效性，在QPZZ-Ⅱ型旋转机械故障试验平台上进行分析。故障试验台如图4所示。试验轴承为6205-2RS型深沟球轴承，其主要参数见表1，采用电火花机在轴承外圈上人工加工一个表面积为0.28 mm2的圆坑点，模拟轴承表面损伤类故障。

振动加速度传感器安装在轴承外壳上采集垂向通道的信号，试验过程中转速为1 478 r/min，转频为24.63 Hz，采样频率为25.6 kHz，计算得轴承外圈故障特征频率为88.30 Hz。

轴承垂直方向上的振动加速度信号如图5所示，可以看到信号中存在幅值比较突出的噪声信号。对振动信号进行EMD分解，得到18个IMF分量，其相关系数及峭度值见表2。由于第6个分量之后的相关系数均过小，表中只列出前6个分量的相关系数和峭度值。

图5 原始信号

表2 各分量的相关系数和峭度值

由表可知：虽然3～6分量的峭度值均大于3，但5，6分量的相关系数较小，与3，4分量相差较大，故选取3，4分量作为最优分量重构信号。重构信号时域图如图6所示，其相关系数为0.32，比3，4分量有所提高；峭度值为4.05,仍高于3。从图6可以看出，原始信号高幅值的噪声信号明显得到抑制，冲击成分得到增强。

图6 重构信号

原始信号的典型谱峭图如图7a所示，从图中可以看出最大峭度处的中心频率为5 607 Hz，带宽取3倍外圈故障特征频率(即264.9 Hz)，将该参数作为共振解调的滤波参数进行共振解调分析，结果如图7b所示，从图中虽然可以观察到外圈故障特征频率88.48 Hz及其2倍频和3倍频，但干扰谱线较多，效果很不理想，说明典型谱峭图算法不稳定，易受噪声等干扰成分的影响，导致轴承优化共振频带确定的失效。

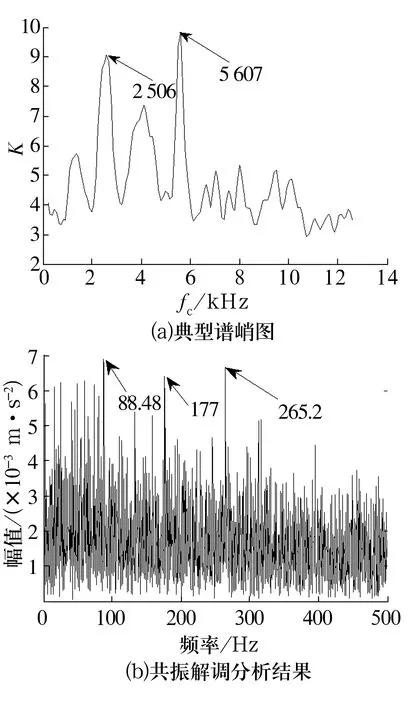
图7 原始信号的典型谱峭图及共振解调结果

对重构信号进行分析，结果如图8所示。从典型谱峭图中可以看出，峭度最大的点为(1 280，19.04)，即中心频率为1 280 Hz。将中心频率1 280 Hz和带宽264.9 Hz作为共振解调的滤波参数，分析结果如图8b所示。从图中不仅可以明显看出外圈故障特征频率88.48 Hz，而且其2倍频和3倍频也具有明显的谱线，可以明确判定故障是发生轴承外圈上，与实际情况相符。

图8 重构信号的典型谱峭图及共振解调结果

为进一步证明有效性，用快速谱峭图对原始信号进行分析，得到中心频率为2 400 Hz，带宽为533.3 Hz，将该参数作为共振解调的滤波参数进行共振解调分析，结果如图9所示。从图中可以看出，故障特征频率处的谱线完全被淹没，虽然可以观察到外圈故障特征频率倍频处的谱线，但其附近包含许多噪声频率干扰成分，效果一般。

图9 基于快速谱峭图的共振解调分析结果

通过以上对比分析表明：利用EMD有效降低了振动信号中的噪声信号，消除了噪声等干扰成分对谱峭度计算的影响，增强了典型谱峭图算法的稳定性，提高了共振解调分析中滤波中心频率和带宽选取的准确性，实现了对滚动轴承故障特征的准确提取。

5 结论

1)该方法有针对性的选取理论计算得到的滚动轴承故障特征频率的3倍频作为滤波带宽，自动搜索最佳的中心频率，弥补了传统共振解调方法在选取带通滤波参数方面需要人工干预的不足。

2)通过相关系数和峭度准则选择最优IMF分量，能有效抑制噪声信号，降低干扰信号对典型谱峭图结果的影响，增强了共振解调频带确定的鲁棒性。

3)通过与基于快速谱峭图的共振解调方法结果对比，验证了该方法提取滚动轴承故障特征的有效性，为滚动轴承故障诊断的研究提供了一个新的途径。