永磁悬浮承载平台的设计及承载力计算分析
刘海娇,周靛,张钢,刘飞,胡慧
(上海大学 机电工程与自动化学院,上海 200072)
磁悬浮支承技术是利用磁场力将被支承物体悬浮于空中,使互相配合的运动部分和静止部分之间没有机械接触的一种高性能支承技术[1]。永磁悬浮技术作为磁悬浮支承技术的一种,具有结构简单,成本低,无需电控系统,可靠性高及承载能力大等诸多优点[2],因而广泛应用于能源交通、航空航天、风力发电等领域[3]。
调谐质量阻尼器是一种附加在结构上的减振子结构,由弹簧、阻尼器和质量块组成。质量块一般通过弹簧和阻尼器支承或者悬挂在主结构上。当结构受到外部荷载作用产生振动时,子结构通过连接装置与结构一起振动,由此产生的能量会通过惯性力反作用于主结构,部分能量被阻尼器所消耗,实现减振的目的。由于调谐质量阻尼系统减振效果明显、占用空间小、便于施工安装维护等优势,在高层建筑、桥梁的减振、抗风工程中有着广阔的应用前景。调谐质量阻尼器主要分为2种:被动调谐质量阻尼器(TMD)和主动调谐质量阻尼器(AMD)。TMD中的质量块通常质量达几十吨甚至上百吨。传统的支承平台采用机械摩擦导轨支承和引导,按给定方向做往复直线运动,虽然定位精确、刚度高、支承性能好,但因为调谐质量阻尼器所支承的质量太大导致摩擦磨损严重,会引起一系列问题。为了改善机械摩擦导轨的摩擦问题,引进了流体摩擦导轨,包括气悬浮支承导轨和液压支承导轨,但是其刚度小、支承性能低且会造成环境污染而得不到广泛应用。
永磁悬浮支承技术具有微摩擦、无磨损、低功耗、无污染、无需润滑和密封等一系列优良特性[4]。虽然永磁悬浮支承技术也存在控制精度低、刚度和阻尼小、装配困难等缺点,但可以通过堆叠以及适当的结构设计实现高承载力、高刚度来满足要求[5]。因此,提出将磁悬浮技术应用于TMD中。永磁斥力型结构能满足7 500 N的承载要求,但所需磁条体积大、成本高,超过市面上常用尺寸,需单独开模,成本大。因此,文中提出了一种基于磁阵列对(Pair of Magnet Array)[6]的吸力型永磁悬浮承载平台,将其应用于调谐质量阻尼器[7]。磁阵列对吸力型结构属于被动磁悬浮系统,比德国的主动电磁悬浮和日本超导磁悬浮系统成本低,结构简单,能耗更小,无需电动控制系统。磁阵列对结构悬浮力大,可满足拉压力要求,系统稳定。
1 永磁悬浮承载平台结构
设计的永磁悬浮承载平台尺寸为300 mm×300 mm,在x方向上行程为±150 mm,要求最大承载能力为7 500 N,刚度为2 000 N/mm。采用多个磁阵列对相互叠加的原理,由移动悬浮磁阵列对插入固定悬浮磁阵列对中而组成永磁悬浮承载平台,其结构如图1所示。条形磁铁如图2所示,磁路垂直于长度方向,图2b中箭头表示磁路方向,即磁铁内磁力线的方向。间隔条材料为磁导率较低的铝合金,能避免相接两磁条形成磁短路。导磁板的作用是为了形成整体的磁回路,降低对周围环境的磁场辐射强度,减少磁泄露,增强整个永磁悬浮支承平台的承载力。磁阵列对所形成的磁路如图3所示。
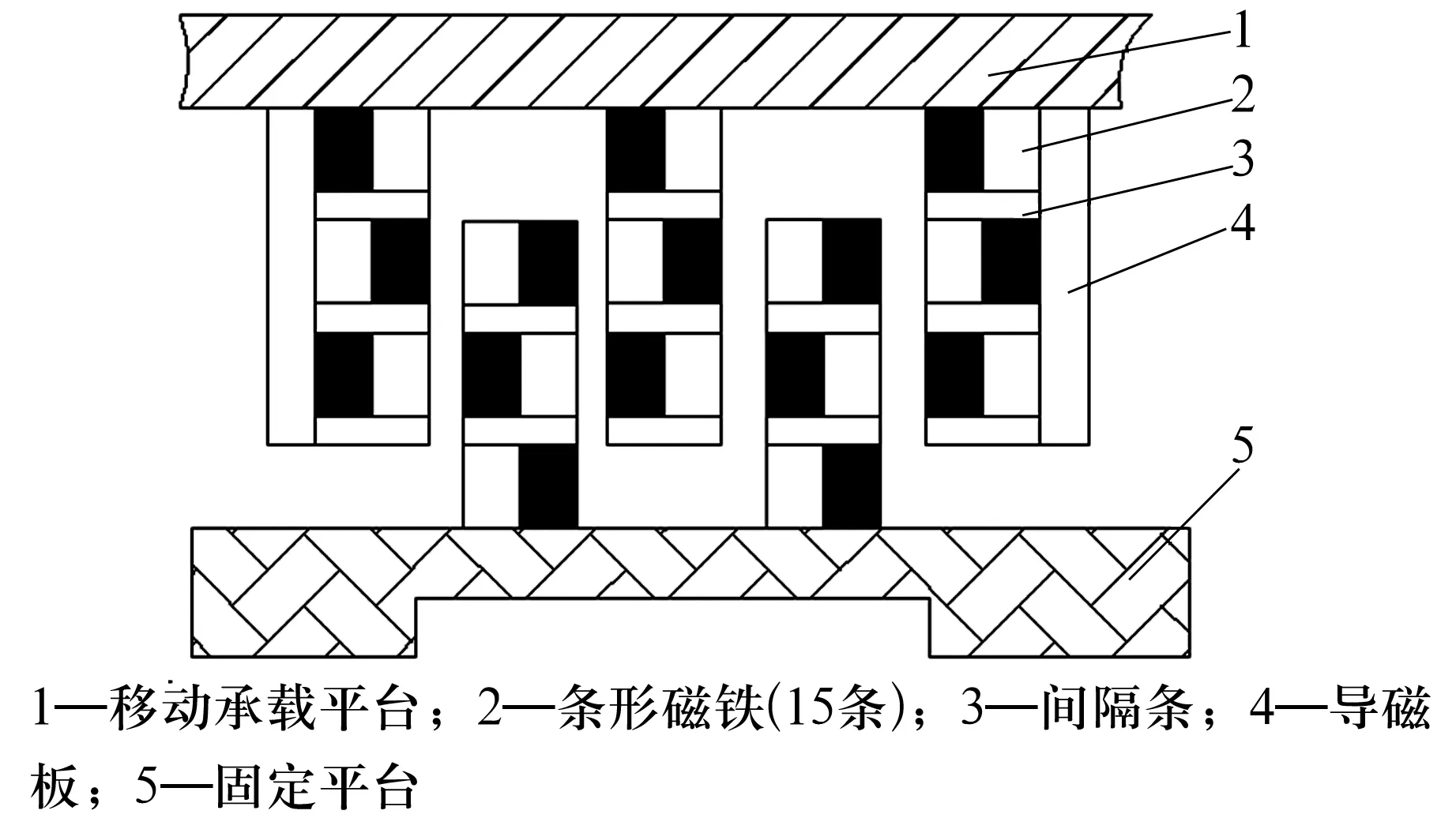
图1 永磁悬浮承载平台结构示意图

图2 条形磁铁

图3 磁阵列对的磁路结构
由图3工作原理可知,当平台承受重力作用时移动承载平台向下移动,固定平台对移动平台向上的力阻止磁阵列对的相对移动。由此可知,磁回路越大,磁阵列对间的相互作用力越大,结构的支承力就越大。因此,必须对整个平台磁路进行磁路优化。运用Ansoft Maxwell软件对整个平台磁回路进行仿真分析,优化前、后的磁力线分布如图4所示。
由图4可知,未添加间隔条与导磁板(优化前)时整个回路小,磁铁边缘磁力线大部分散去,没有得到很好利用;添加上间隔条和导磁板(优化后),磁力线回路增加,边缘磁力线通过导磁板回到磁铁,减少了磁泄漏,磁力线得到很好利用。
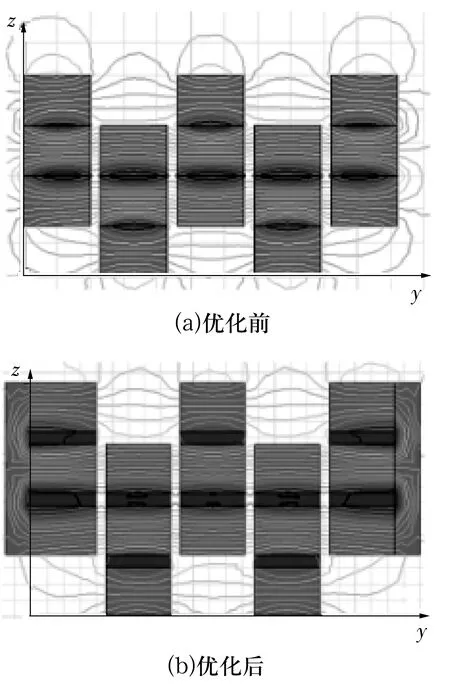
图4 磁阵列对组磁路优化
1.1 磁条的尺寸、材料选择
2块永磁体的物理模型如图5所示,2块条形磁铁磁路方向沿y向,两永磁体磁极串联。条形磁铁宽度为b,高度为a,长度为l,两磁铁间隙为c。矩形截面的矩形永磁体在宽度b与高度a相等时永磁体间的磁力最大[8]。
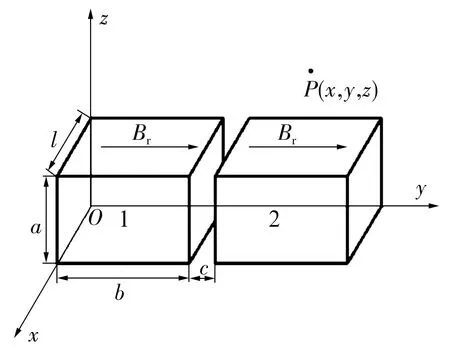
图5 条形永磁体力作用解析模型
永磁体材料有很多种,设计中要根据实际工况合理选择。几种常用永磁材料的性能特点见表1,其中,永磁材料的主要技术性能指标包括:剩磁Br、矫顽力Hc、内禀矫顽力Hcj、磁感矫顽力Hcb、磁能积(BH)m和居里温度TC。

表1 常用永磁材料的性能特点
由表可知,AlNiCo剩磁较高,较容易加工,但矫顽力低,易脆,价格昂贵;粘结铁氧体具有很好的加工特性和材料特性,但材料矫顽力和剩磁都低;NdFeB在常温下具备较高的永磁性能,但材料韧性差,不易加工。文中设计的永磁悬浮试验平台工作温度为常温,要求控制成本,并保证磁场强度,因此,结合永磁材料的特点及实际应用条件,选用烧结NdFeB永磁材料。
1.2 间隔条的尺寸选择
由磁阵列对原理[6]可知,堆叠磁条过程中必须在磁条之前加入间隔条,间隔条的作用是避免上下相邻长磁条间的磁力线被过分短路,使更多的磁力曲线形成大回路,以增加结构的承载力。运用Ansoft Maxwell对磁力进行分析如图6所示,其中,e为间隔条尺寸,c为磁铁间隙。由图6可知,当e≤c时,上下堆叠的磁条为异性磁极部分磁力线形成回路;当e>c时,磁力曲线几乎全部形成大回路。因此,在磁阵列结构中,必须满足间隔条的厚度要大于磁条之间的间隙。但间隔尺寸太大又会使结构尺寸增大,磁路长度增加,且影响磁阵列的强度,增加安装难度。

图6 间隔条尺寸影响示意图
NbFeB材料较脆、易裂、机械性能较差,考虑到安装过程的需要,在间隙两侧磁阵列对外层各敷一层厚度为1 mm的自润滑材料,并留1 mm的间隙,因此,取c为3 mm,e为4 mm。
1.3 导磁板的尺寸选择
合理选用导磁板,可以使磁路更大程度的聚拢,提高承载力。钢铁材料导磁性能好,造价低,易于加工且具有一定的刚度。因此,选用Q235材料,其饱和磁感应强度为1.8 T,BH曲线如图7所示。
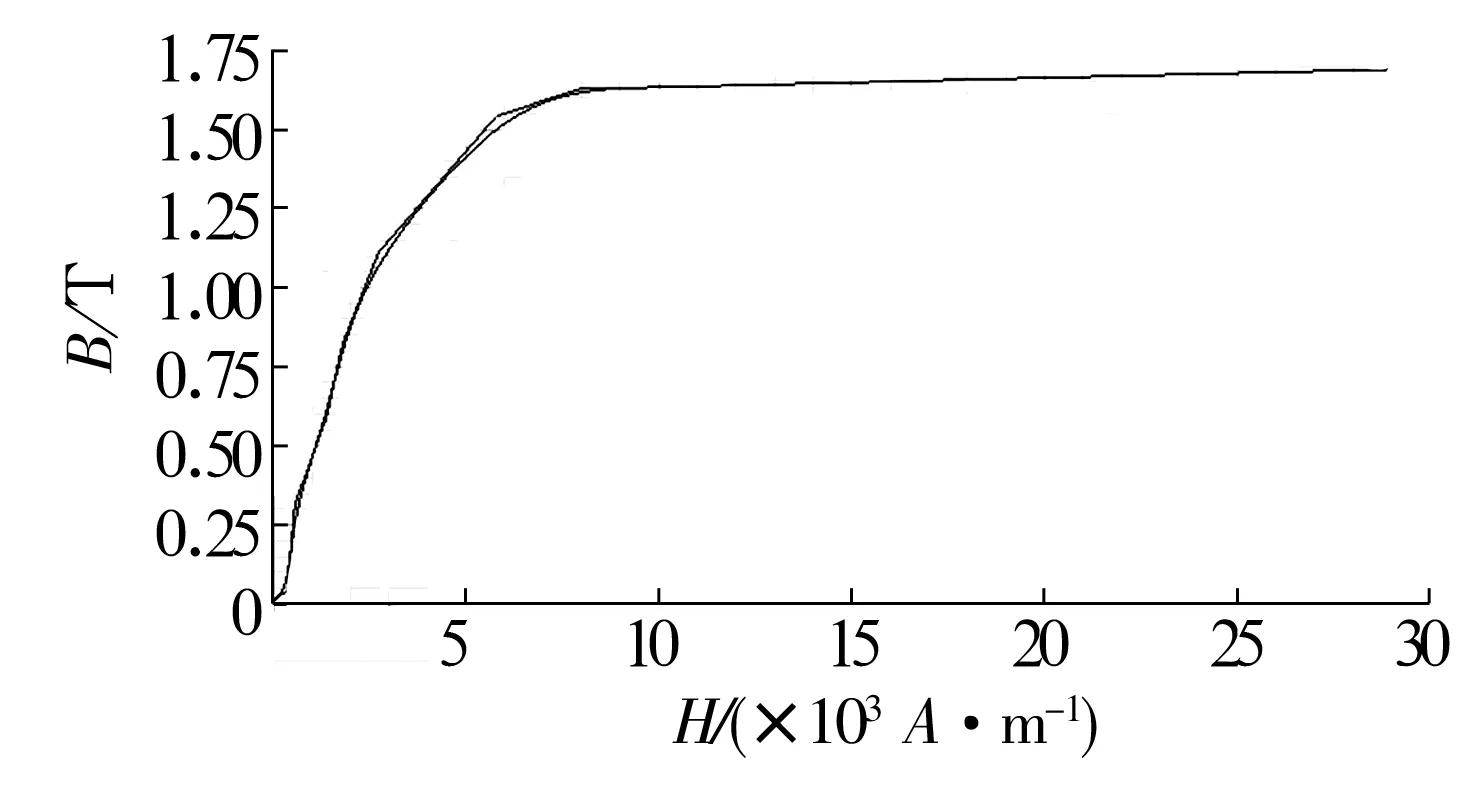
图7 Q235材料的BH曲线
不同导磁板厚度对磁力线产生影响。根据磁通连续性原理,在不考虑漏磁的情况下,外磁路的总磁通Φ应与永磁体内部的磁通Φm相等。即
Φ=Φm,
(1)
Φ=BδSδ,
(2)
Φm=BmSm,
(3)
式中:Bδ为气隙磁密;Sδ为磁极与导磁板接触面的截面积;Bm为永磁体磁极表面磁密;Sm为永磁体工作气隙的磁极表面积。
将(2),(3)式代入(1)式,得
BmSm=BδSδ。
(4)
根据经验可知,永磁体工作点的磁感应强度最大值为永磁体剩磁的50%,即
从而得到
其中,Sδ=20 mm×100 mm,Sm=d×100 mm,d≥6.7 mm,所以导磁板的厚度选为8 mm。接着运用Ansoft Maxwell软件对8 mm厚导磁板磁密分布进行仿真分析,仿真结果如图8所示。

图8 8 mm厚导磁板磁密分布图
由图8可知,导磁板最大磁感应强度为1.75 T,小于饱和磁感应强度1.8 T。因此,选择导磁板厚度为8 mm,长度和高度与磁阵列对结构保持一致。
2 磁阵列对结构的力学分析
依照文献[9]给出的磁力计算方法,推导出整个平台的计算方法。通过对几组不同尺寸条形磁铁磁力的计算及仿真,确定磁力与体积的关系。最终运用Ansoft Maxwell对整个设计平台的承载力进行仿真计算,并通过计算数据分析此平台是否满足设计需要。
2.1 两个磁条之间磁力的解析模型
文献[9]给出了永磁铁1在磁体外任何一点P处的磁感应强度大小(图5),即
(5)
(6)
(7)
(8)
式中:x1=x,x2=x-l,y1=y,y2=y-b,z1=z,z2=z-a。由对称性可知,Fx=0,Fz=0,则只需要对y方向磁力进行计算。由文献[10]可知,导磁材料磁导率μr远大于1,则磁铁间磁场力为
(9)
式中:μ0为真空磁导率;B为磁场与导磁材料作用面处的磁感应强度;S为磁场与导磁材料作用面的面积。磁铁1,2间磁感应强度为
(10)
两磁铁间磁力为
(11)
NdFeB永磁体材料的矫顽力Hc=907 000 A/m,相对磁导率μr=1.067,可得Br=μrμ0Hc=1.21 T。磁铁尺寸为a×b×l,取a=b,l=100 mm;磁铁之间的气隙取c=3 mm。对不同尺寸b(a)运用磁力模型的计算结果和仿真计算结果进行对比,见表2。

表2 Ansoft Maxwell仿真磁力与计算磁力
由表2可知,计算值略小,可以考虑加一个常数参数K来调节计算值,使之更加接近仿真数据。参数K根据仿真磁力和计算磁力进行加权确定
(12)
代入数据可得K=1.128。
增加系数后磁力解析表达式为
(13)
再次计算结果对比见表3,计算数据和仿真数据基本一致。需要注意的是,解析表达式(13)只能作为工程设计时初步的参数参考,大概确定尺寸范围,并不能保证较高的精度,在初步确定磁条的基本参数之后仍需要用其他更加精确的仿真方法进行计算,对数据进行验证和修正,以达到较优结构。

表3 Ansoft Maxwell仿真磁力与增加参数计算磁力对比
2.2 磁阵列对单元的支承力计算
分别运用理论计算和Ansoft Maxwell模拟计算2种方法对整个永磁悬浮承载平台的承载力进行计算。
如图9所示,磁阵列对由n条磁条通过排列组成,通过磁路优化形成磁回路、形成支承力。为了方便计算,对该结构进行力学模型解析,单个磁阵列对组结构可近似看做8对异性磁极之间吸力和12对同性磁极斥力的组合。
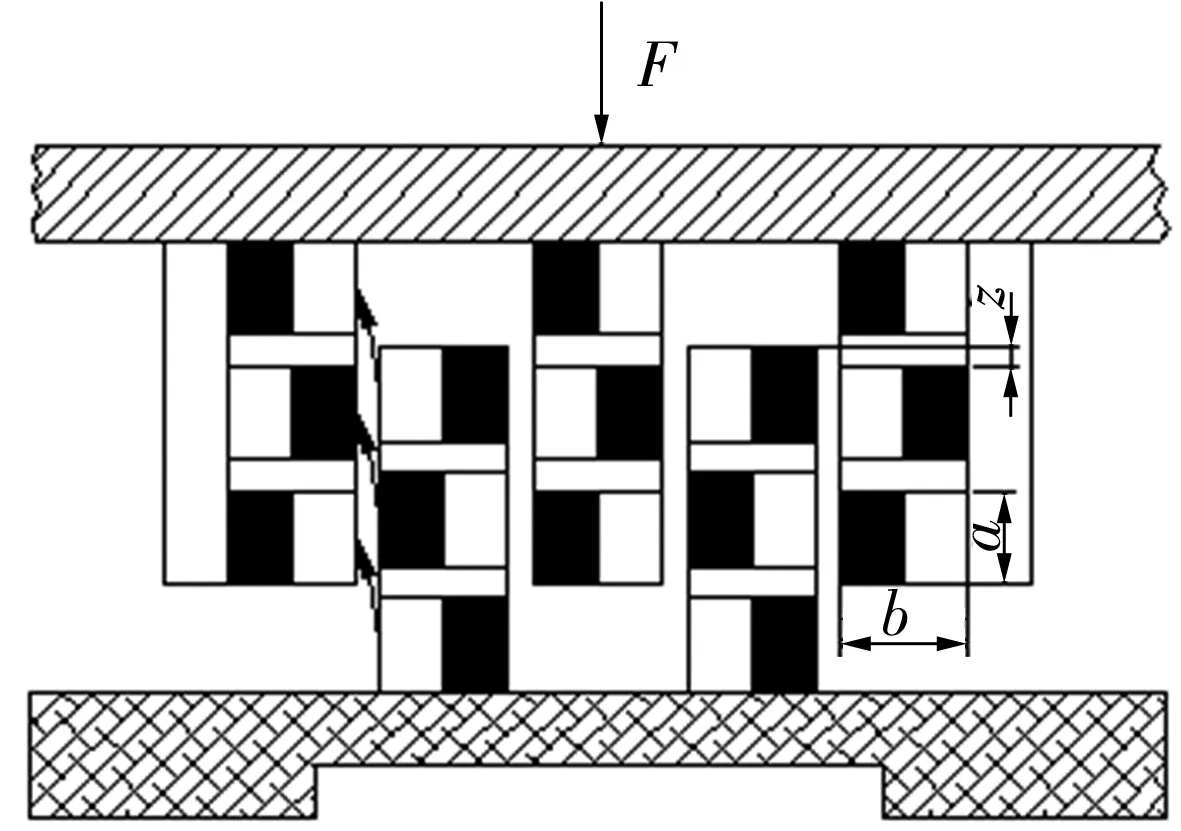
图9 磁阵列对组力作用的示意图
由图10可知,单个磁阵列对组单元的承载力为
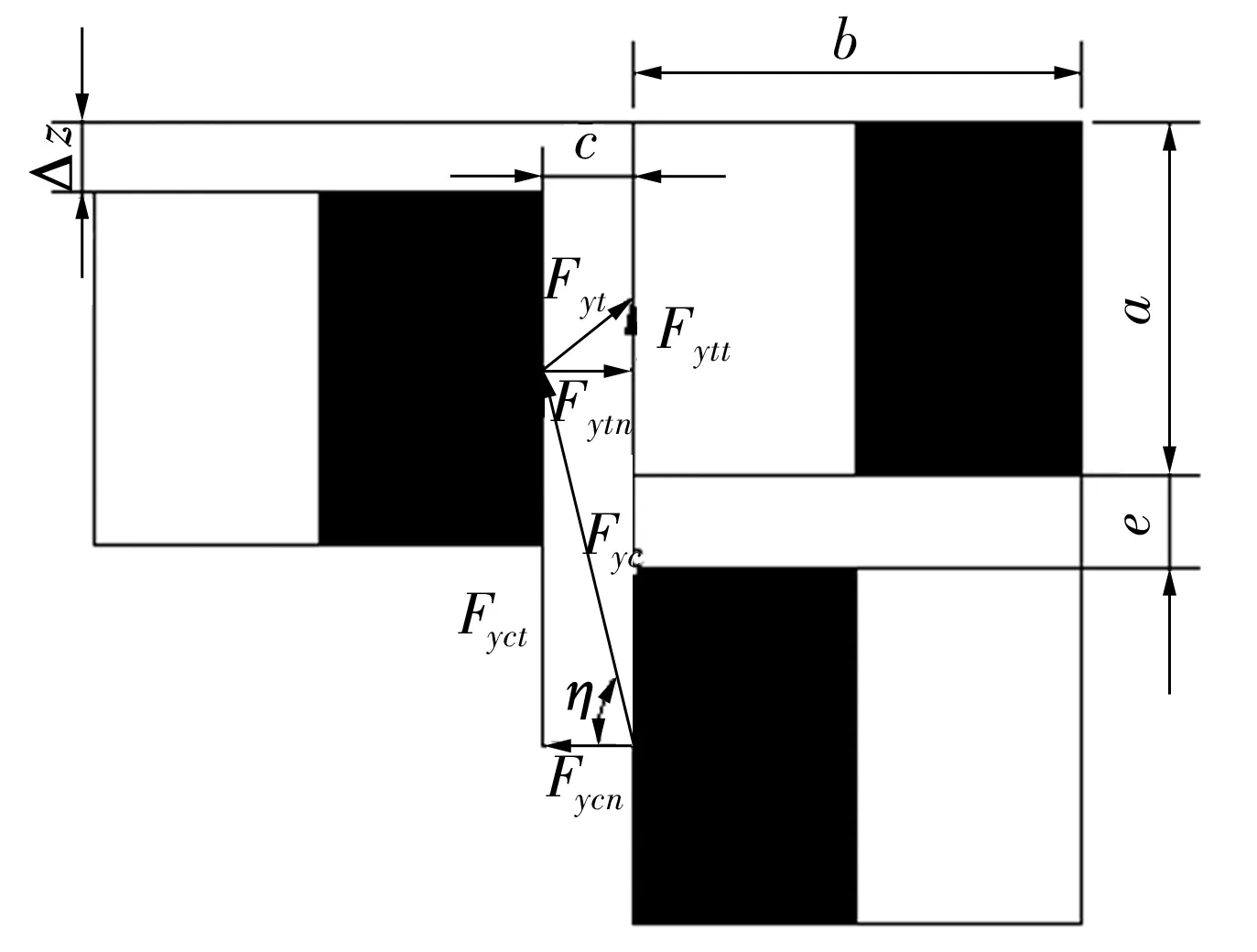
图10 磁阵列对中磁极之间作用力示意图
Fi=8Fytt+12Fyct=8Fytsinθ+12Fycsinη,
(14)
(15)
(16)
图中,Fytt为相对异性磁极之间吸力Fyt向上的分力,同理Fyct为同性磁极之间斥力Fyc向上的分力。为了方便计算,磁条拟取N35型NbFeB材料并假设不考虑移动平台自重,间隙c=3 mm,在平台承受力F的情况下移动平台下移Δz=1 mm。为了验证其准确性,选用5组尺寸(a×b×l)分别为10 mm×10 mm×100 mm,13 mm×13 mm×100 mm,15 mm×15 mm×100 mm,18 mm×18 mm×100 mm,20 mm×20 mm×100 mm,分别利用数学解析模型和Ansoft Maxwell仿真计算所得结果见表4。

表4 不同尺寸磁阵列对组的承载力仿真与计算结果对比
由表4可知,Ansoft Maxwell仿真结果比将磁阵列对简化成n对磁条之间磁力之和计算出来的结果大,相对误差随着磁铁体积增加而减少。这说明单个磁阵列对组不是简单相对的两磁条之间的磁力累加,而是具有自强化效应,再加上磁路优化,使得承载力大大增加。
由表4得到单个磁阵列组对的仿真承载力与磁条体积关系如图11所示。由图可知,单个磁阵列对组的承载力随着单个磁条的体积增加而增大,并近似成线性分布,近似表达式为
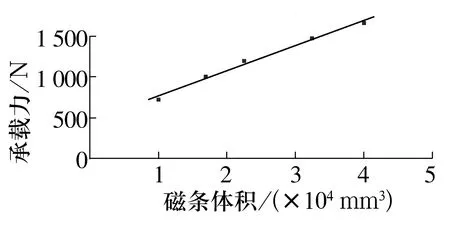
图11 单个磁阵列对组的承载力与磁条体积的关系
Fi=0.031V+459.36,
(17)
说明磁铁尺寸越大,承载力越大,也验证了经验的正确性。
2.3 Ansoft Maxwell软件仿真
建立仿真模型如图12所示,定义材料属性(磁性材料参数如上述);间隔条采用铝合金,相对磁导率设置为μr=1.000 21;导磁板采用Q235,相对磁导率设置为μr=4 000。

图12 磁阵列对组在Ansoft Maxwell中的仿真模型
边界采用系统默认边界,并将固定磁阵列设置了加载力,定义求解域为实体的50倍,最大迭代次数为20次,迭代误差不超过1%。网格划分设置为永磁体最大5 mm,网格划分结果如图13所示。
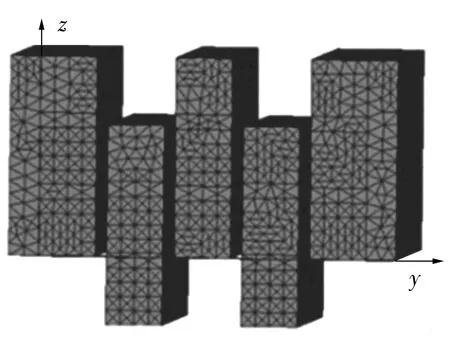
图13 Ansoft Maxwell中磁阵列对组模型的网格划分
通过调节固定磁阵列对z向的位移Δz,Ansoft Maxwell仿真求解得出单个磁阵列对组的承载力和整个试验台(6组)的承载力结果见表5。
由表5数据可知,承载力F随着z向位移Δz的绝对值增大而逐渐增大,将数据绘制成曲线(图14)可见,近似为2条满足线性关系的直线。由图可知,当Δz≤4 mm时,近似表达式为
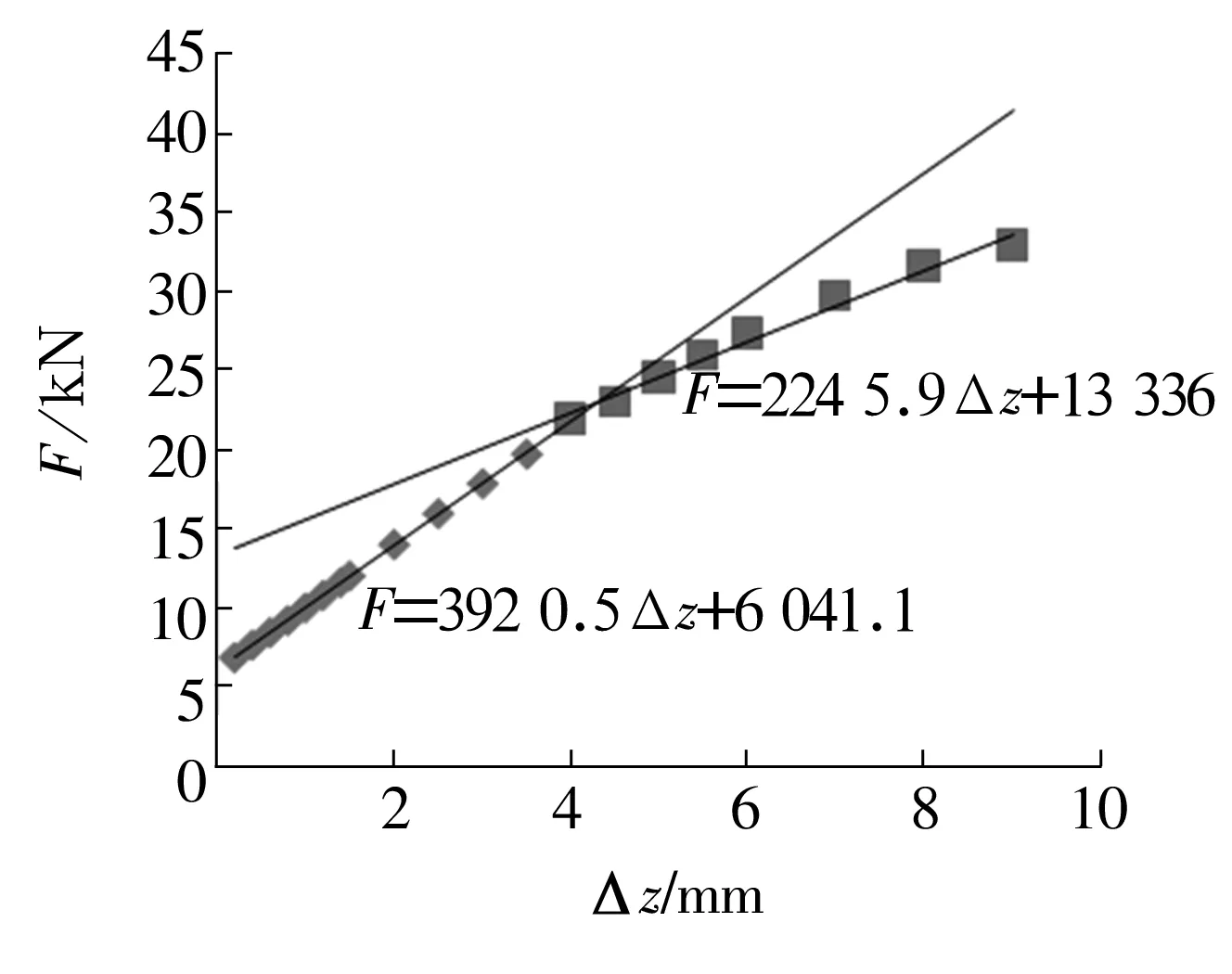
图14 承载力仿真结果F随位移Δz的变化曲线

表5 不同位置时试验台承载力的仿真结果
F=3 920.5Δz+6 041.1。
(18)
当Δz>4 mm时,近似表达式为
F=2 245.9Δz+13 336。
(19)
仿真结果表明,当磁条位移小于间隔条厚度(4 mm)时,试验台z向刚度Kz1=3 920.5 N/mm;当磁条的位移大于间隔条的厚度时,试验台z向刚度Kz2=2 246 N/mm。Δz≤4 mm时的刚度要远远大于Δz>4 mm时的刚度,因此在结构执行过程中,应当使试验台在z向最大位移Δz不超过4 mm。
整个平台承载可通过选择磁阵列对数及z向移动距离Δz实现悬浮承载,承载力达到5 000~20 000 N,完全可以满足整个平台的设计要求(最大承载力7 500 N,刚度2 000 N/mm)。设计的永磁悬浮承载试验台三维图如图15所示。

图15 永磁悬浮承载试验台三维图
3 结束语
利用Ansoft Maxwell软件对吸力型永磁平台承载力进行了分析,得出结论:
1)在磁路设计中,磁体尺寸参数确定十分重要,磁体选择过大,材料浪费,反之达不到所要求性能,一般充磁方向宽度b和高度a相等时永磁体间的磁力最大。
2)采用Ansoft Maxwell仿真的磁力结果比将磁阵列对简化成n对磁条之间磁力之和计算出来的结果大,相对误差随着磁铁尺寸增加而减少。说明磁阵列对不是简单相对的两磁条之间的磁力累加,而是具有自强化效应。整个平台的承载力达到5 000~20 000 N。
3)仿真结果表明,当移动承载平台的磁条移动位移小于间隔条厚度(4 mm)时,整个平台的承载刚度为3 920 N/mm,当大于间隔条厚度时,平台刚度为2 246 N/mm,刚度减小,因此,设计时应保证满足承载要求情况下,移动位移小于间隔条厚度。

