基于RomaxCLOUD的角接触球轴承轴向刚度计算分析
严小云,朱永生,牛青波,李江艳,张进华
(1.西安交通大学 现代设计与转子轴承系统教育部重点实验室,西安 710049;2.洛阳轴承研究所有限公司,河南洛阳 471039;3.沈机集团昆明机床股份有限公司,昆明 650203;4.西安交通大学 机械制造系统工程国家重点实验室,西安 710049)
角接触球轴承作为机械回转结构的核心支承组件,广泛应用于精密机床、汽车、航空飞机等重大设备中。轴承刚度对于系统支承性能有重要影响,接触角作为精密角接触球轴承结构设计中的重要结构参数,不仅会影响轴承的受力、润滑、寿命,也会对其刚度产生显著影响。
目前,很多学者在角接触球轴承接触特性与刚度方面做了大量的研究工作。文献[1-2]建立了轴承静力学及接触测试等分析模型;文献[3]以轴承拟静力学模型为基础,研究了轴承作用力和电主轴转速对轴承刚度的影响;文献[4]结合Hertz接触理论和轴承套圈控制理论,考虑轴承运行中钢球的离心力和陀螺力矩建立了球轴承拟静力学模型;文献[5]基于轴承拟静力学与沟道控制理论研究了轴承装配过程中过盈配合量、预紧力对于高速角接触球轴承径向、轴向以及角刚度的影响规律;文献[6]在拟静力学的基础上分析了预紧力和接触角对轴承刚度的影响;文献[7]基于沟道控制理论的5自由度拟静力学模型对角接触球轴承进行建模,分析了预紧力以及转速对轴承刚度的影响;文献[8-10]采用有限元法对比分析了轴承接触应力分布、变形及刚度变化的特征;文献[11]基于BP神经网络方法研究分析了接触角和转速对轴承轴、径向刚度的影响。
在高速运行条件下,轴承的接触角对其刚度性能的影响显著,文中基于RomaxCLOUD建立高速精密角接触球轴承模型,利用计算较为快速且准确的轴承拟静力学计算方法分析接触角对轴承刚度的影响,并与经验公式计算结果对比。
1 轴承刚度计算经验公式
轴承刚度是轴承内外圈在载荷方向上产生单位弹性位移量所需要的外载荷,可表示为
(1)
式中:F为载荷;δ为轴承内外圈在载荷方向上发生的弹性位移。
角接触球轴承在纯轴向载荷Fa的作用下,假定受力后接触角仍为初始接触角,则轴承所受载荷与位移的关系为[12]
(2)
式中:Kn为轴承刚度系数;Z为球数;α0为初始接触角;δa为轴向位移。
轴承轴向刚度计算公式为
(3)
计算时不仅需要轴承接触角和球数等参数,还需计算轴承刚度系数Kn。由文献[13]可知,轴承的轴向刚度还可用经验公式表示为
Ka=16.5×104Z(Dwδasin5α0)1/2,或
Ka=0.344×104(DwFaZ2sin5α0)1/3,
(4)
式中:Dw为球直径。
但在实际应用中受载后接触角将发生变化,(4)式并未充分考虑轴承在受载情况下接触角的变化,故公式存在一定偏差。为分析经验公式的适用范围,可将经验公式与轴承拟静力学计算的轴承刚度结果进行对比。
2 拟静力学分析方法
拟静力学方法在分析轴承力学性能时,考虑了惯性力作用下的轴承稳态运转特性,可以有效预测球的自转和公转速度、轴承变形和刚度。轴承受轴向、径向、离心载荷的作用,接触角会发生变化,从而影响轴承的刚度。
2.1 轴向载荷对轴承接触角的影响
假设轴承匀速运动,忽略球与保持架之间的作用力,轴承受到纯轴向载荷作用时各个球受力相同。根据Hertz接触理论,球与套圈之间的接触载荷和弹性变形的关系为
Fa=kδ3/2,
(5)
式中:k为球与套圈之间的载荷-变形系数。
各个球所受载荷均匀分布,每个球所受载荷为
(6)
式中:α为轴承受载后的实际接触角。
角接触球轴承受到轴向载荷时接触角将增大,如图1所示。受载后,球与套圈之间的接触变形δ等于内外沟曲率中心之间距离的变化量。
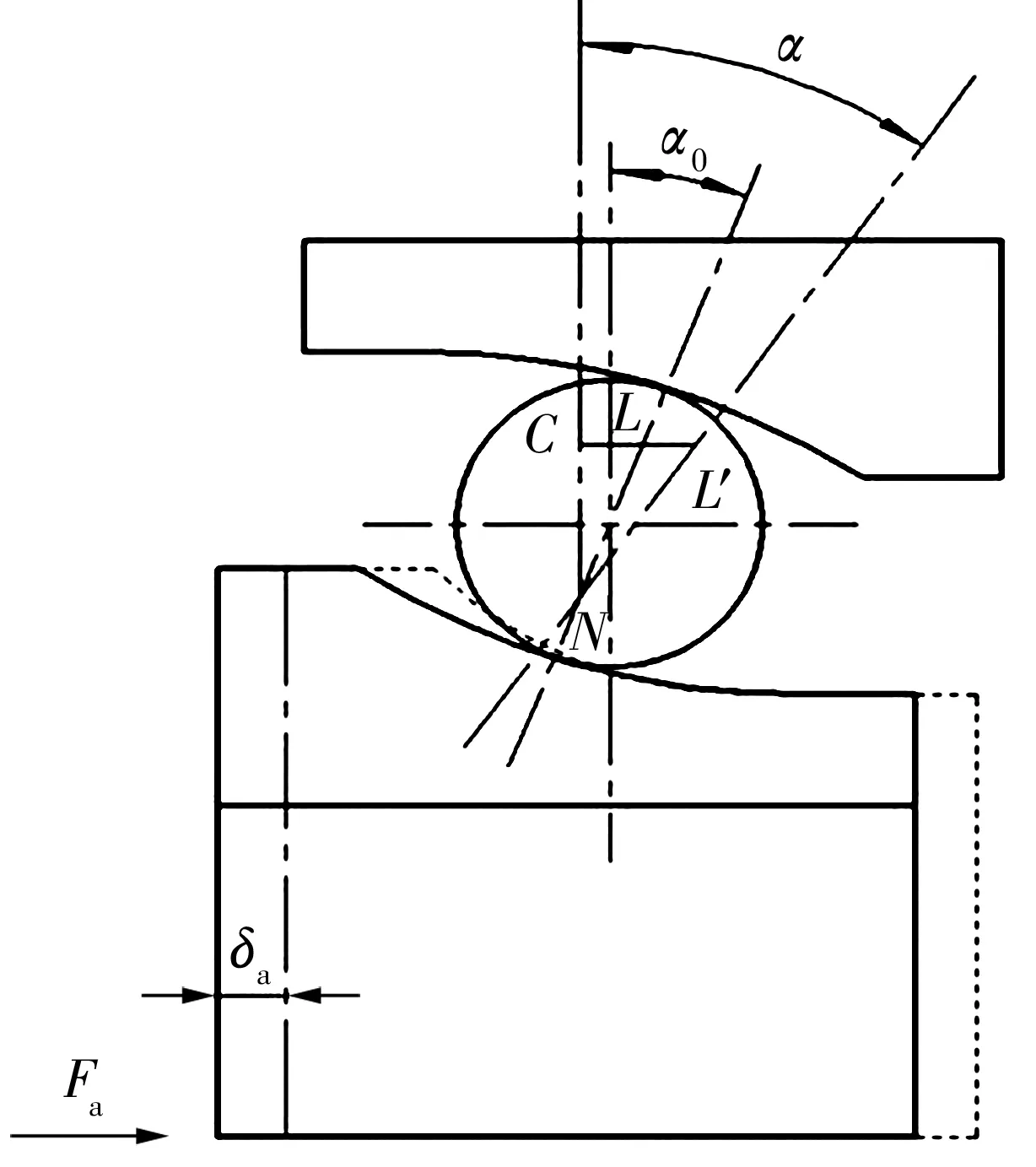
图1 接触角变化示意图
由图1几何关系可知
NL′=NL+δ=BDw+δ,
(7)
B=fi+fe-1,
LC=NLcosα0=NL′cosα,
(8)
式中:fi,fe分别为内、外圈沟曲率半径系数。
根据(7),(8)式可得
(9)
(10)
式中:kp为载荷-变形常数。
由(9),(10)式可知,轴承受到轴向载荷时,接触角变化会对球的受力以及轴承的轴向位移有直接影响。
2.2 径向载荷对接触角的影响
在受径向载荷时,内圈相对于外圈发生轴向位移δa和径向位移δr。不同位置的球承受的载荷及变形量不同,每个球接触角不同。轴承中每个球的相对角位置ψ如图2所示。
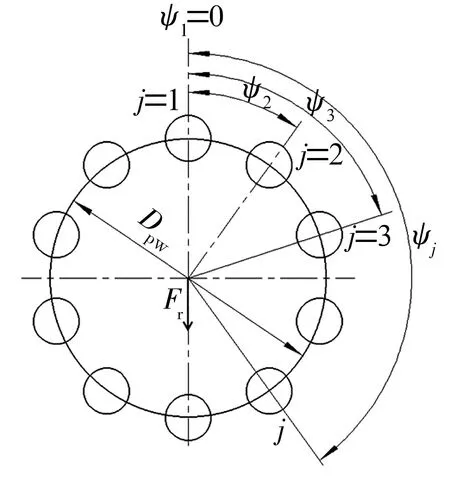
图2 球的角位置
角位置ψj处第j个球的弹性变形量为
δj=[(Bsinα0+δa)2+(Bcosα0+
(11)
以内圈为分析对象,轴承处于平衡状态时
(12)
由(11),(12)式得
sinαj=
(13)
cosαj=
(14)
由(13),(14)式可知,轴承受径向载荷时,轴承每个角位置处球的受载不同,导致对应不同位置的球的接触角发生变化。
2.3 离心载荷对接触角的影响
当轴承高速运转时,球离心力和陀螺力矩的作用不能被忽略,第j个球的离心力为
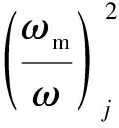
(15)
陀螺力矩为
(16)
式中:m为单个球的质量;Dpw为球组节圆直径;ω为轴承的角速度;J为球对质心轴的转动惯量;ωm/ω,ωR/ω分别为轴承的自旋比和旋滚比。
β可表示为
(17)
由于离心力和陀螺力矩的作用,球与内外沟道的接触角发生了变化,使得内、外圈曲率中心点与球心不再共线(图3),内圈接触角由αi增大为αij,外圈接触角由αe减小为αej。图3中,A1j为两沟道曲率半径中心距;X1j为球与外沟道沟曲率中心水平距离。
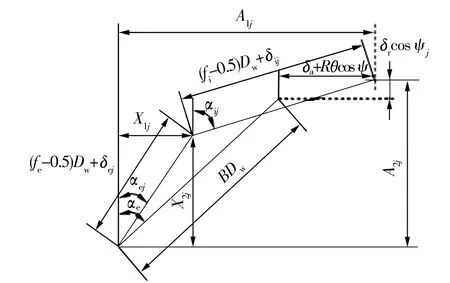
图3 球心与沟道曲率中心的位置
轴承高速运转时,球在轴向和径向需保持受力平衡,其平衡方程为
λejcosαej)=0,
(18)
λejsinαej)+Fcj=0,
(19)
由(18),(19)式可得轴承内外圈接触角为
(20)
由以上分析可知,轴承受到离心载荷作用时,球的接触角发生变化。
3 基于RomaxCLOUD的轴承参数计算
基于RomaxCLOUD的轴承浏览与设计功能可得到轴承的主要参数[14],根据已有标准轴承的参数,输入目标设计参数,即可得到不同设计参数下轴承的其他参数以及标准图纸。以7014C轴承为例,其主要参数见表1。

表1 主要设计参数
为分析轴承初始接触角与轴承刚度之间的关系,在利用拟静力学方法计算轴承刚度时,除表1中的参数外,还需要确定在不同接触角下轴承外圈沟底直径de以及轴承的球组节圆直径Dpw。基于RomaxCLOUD的设计功能得到7014C轴承在几种常见接触角下的外圈沟底直径de以及球组节圆直径Dpw,见表2。
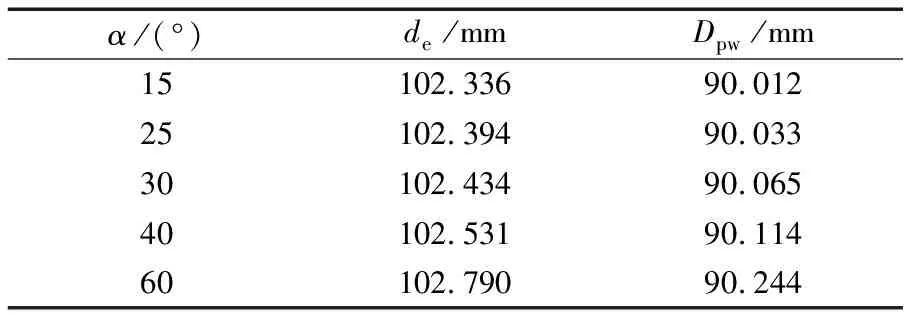
表2 不同接触角下7014C轴承的de和Dpw
4 刚度计算结果及分析
假定轴承受载后内外接触角相等,用经验公式和拟静力学方法分别计算轴承在不同初始接触角时的轴向刚度,拟静力学轴承刚度计算方法可参考文献[7]。
4.1 经验公式和拟静力学方法计算轴向刚度
在初始接触角为15°,25°,30°,40°,60°状态下,设定径向载荷为0,分别用经验公式和拟静力学方法计算角接触球轴承的轴向刚度,计算结果如图4所示。
从图4可以看出,角接触球轴承初始接触角为15°,25°,30°时,经验公式与拟静力学计算的轴承轴向刚度结果之间存在较大的误差,经验公式计算值比拟静力学计算角偏小,随轴向载荷增大,误差逐渐增大。接触角为40°时,经验公式与拟静力学计算的轴向刚度结果之间误差最小。接触角为60°时,经验公式与拟静力学计算的轴向刚度结果之间误差较小,经验公式计算值比拟静力学计算值偏大。
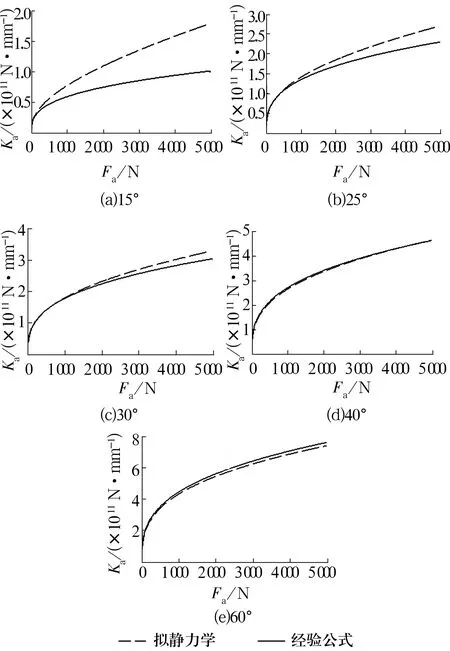
图4 不同接触角下轴承轴向刚度
不同接触角下经验公式与拟静力学计算轴承轴向刚度误差如图5所示,从图5可以看出在角接触球轴承接触角为15°,25°,30°,60°时,经验公式与拟静力学方法计算的轴承轴向刚度之间的误差随着轴承所受轴向载荷的增大逐渐增大。而接触角为40°时,经验公式与拟静力学方法计算的轴承刚度之间的误差随着轴承所受轴向载荷的增大逐渐减小。
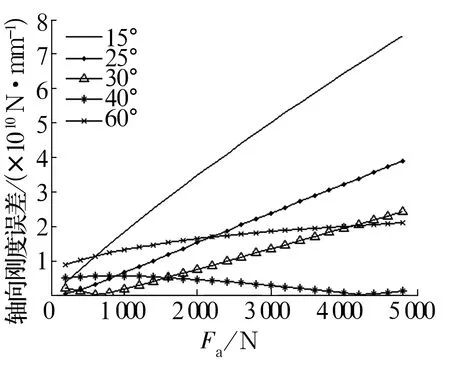
图5 不同接触角下经验公式与拟静力学计算轴承轴向刚度误差
4.2 轴承接触角变化分析
由于轴承拟静力学刚度计算方法考虑轴承在受到轴向载荷后接触角的变化,计算的刚度结果更为准确。经验公式与轴承拟静力学方法计算的刚度之间的误差可能是由于经验公式未能考虑轴承在受载后接触角变化。
4.2.1 轴向载荷对轴承接触角的影响
拟静力学计算方法中角接触球轴承所受轴向载荷会使轴承接触角发生变化。设定轴承所受径向载荷为0,对其施加轴向载荷,计算不同初始接触角时,轴承接触角随轴向载荷变化如图6所示。
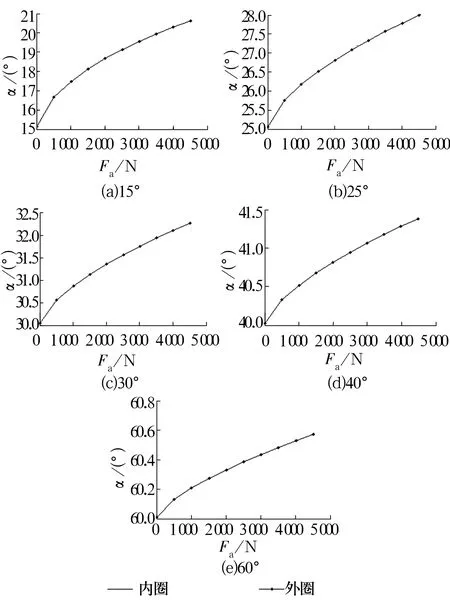
图6 不同接触角下实际接触角随轴向载荷的变化
由于拟静力学计算中转速设置为0,所以计算结果中轴承内外圈接触角相等。从图6可知,随初始接触角增大,轴承在受到相等轴向载荷时,轴承接触角的变化逐渐减小。
4.2.2 径向载荷对轴承接触角的影响
初始接触角为15°,轴承轴向载荷为1 000 N,转速为1 000 r/min,在不同径向载荷时,分析每个球与内、外圈之间接触角的变化趋势。
轴承受径向载荷时,不同位置处球的弹性变形不同,每个球与内、外圈之间的接触角也不同,19个球接触角的变化趋势如图7所示。球接触角的变化随球在轴承中位置角的变化而变化,受载最大的球,内外圈对球压的最紧,使得接触角最小;受载最小的球,内外圈对球压得最松,接触角最大。随径向载荷的增加,接触角的变化范围增大。

图7 不同位置球接触角随径向载荷的变化
4.2.3 离心力对轴承接触角的影响
初始接触角为15°,轴向载荷为1 000 N,径向载荷0时,分析轴承在不同转速下球与内、外圈之间接触角的变化趋势。
球受离心力和陀螺力矩的作用,使其与轴承内、外圈之间的接触角随转速变化,如图8所示,外圈接触角随转速的增大而减小,内圈接触角随转速增大而增大。

图8 轴承内、外圈接触角随转速的变化
5 结论
1)通过分析角接触球轴承在初始接触角为15°,25°,30°,40°,60°时,经验公式与拟静力学方法计算的轴承轴向刚度之间的误差,得出角接触球轴承在初始接触角较小时,经验公式与拟静力学方法计算的轴向刚度结果之间有较大的误差。经验公式的计算结果较拟静力学方法的计算结果偏小。在接触角为40°时,两者计算结果误差最小,接触角为60°时,两者计算的轴承轴向刚度结果之间的误差较小,经验公式较拟静力学的计算结果偏大。
2)在已知某型号轴承的主要设计参数时,若要估算该型号轴承在其他初始接触角状态下轴承的轴向刚度性能。初始接触角较大时,可使用经验公式快速计算出轴承的轴向刚度。轴承初始接触角较小时,经验公式的计算结果只能作为参考值。轴向载荷、径向载荷、离心力及陀螺力矩都会对轴承初始接触角产生较大的影响,经验公式未考虑这些参数的影响,应采用拟静力学方法计算轴承在不同接触角时的轴向刚度。

