水平风洞中开展飞机尾旋特性研究的理论分析

郭林亮，祝明红，傅澔，杨洪森，钟诚文

1. 西北工业大学 航空学院，西安 710072 2. 中国空气动力研究与发展中心 低速空气动力研究所，绵阳 621000

尾旋作为飞机最复杂、最危险的极限飞行状态之一，以超临界迎角、大侧滑角、显著的滚转角速度及偏航角速度为主要特征。由于尾旋中飞机的操纵性显著变坏甚至完全丧失，同时空间方位判断及驾驶条件变得更为复杂，因而对飞行员及飞机的安全构成了极大威胁。因此，飞机的大迎角失速偏离、尾旋特性预测以及尾旋改出方法，都是飞机气动设计和地面试验中非常重要的研究课题。

现有飞机尾旋相关的研究手段主要有飞行仿真和试验两大类。其中飞行仿真手段侧重于解析分析，主要包括非线性分叉分析、延拓算法研究、数值飞行动力学仿真及基于飞行模拟器的半物理仿真等，其所需的气动力数据由风洞试验获得，主要有大迎角静态试验、动导数试验、旋转天平试验3类[1-3]。近年来，NASA开展了缩比大型运输机的气动力建模、分叉分析仿真及尾旋试验研究[4]，欧盟第七框架项目SUPRA开展了大型飞机针对极限飞行条件下移动基模拟器的飞行员评价仿真研究[5-6]。理论研究中一些新的尾旋敏感性分析方法相继提出，如SNB(Saddle-Node Bifurcation)准则[7]、非线性指数理论(Nonlinearity Index Theory)[8],这些方法为飞机尾旋预测提供了新的途径，但需要相应试验方法的验证和支持。试验手段主要包括立式风洞尾旋试验、缩比模型大气自由飞试验以及原型机的尾旋试飞等[9-10]。立式风洞尾旋试验主要研究飞机稳定尾旋特性及改出操纵方法，其环境可控、成本低廉、效率较高，但无法模拟尾旋进入阶段；缩比模型的大气自由飞试验可进行尾旋进入、发展和改出全过程的研究，但系统复杂、耗费较高、效率有限；原型机试飞是为设计定型开展的验证飞行，其结果真实可靠，一般仅在设计研制过程的最后阶段开展。

近年来发展的风洞虚拟飞行技术是典型的针对非线性气动问题的试验手段，能够较为逼真地模拟机动飞行过程，更好地揭示气动/运动的耦合机理。该技术最早由美国人提出概念并由Magill等在乔治亚州42 in×43 in(1 in=25.4 mm)风洞进行了首次虚拟飞行的演示试验[11-14]，随后其他国家也开展了类似的研究。英国Bristol大学设计了低速风洞3自由度和5自由度动态装置，发现了Hawk模型大迎角下的极限环振荡现象，并实现了该模型绕速度矢滚转动作[15-19]。俄罗斯Sohi发展的腹撑3自由度装置开展了典型战斗机稳定尾旋的试验研究，但没有对系统动力学进行理论建模分析，机构中的运动曲杆和摩擦力矩对试验结果的影响尚未涉及[20]。俄罗斯TsAGI提出了一种背撑3自由度装置，采用鲁棒控制方法对机翼摇滚问题进行了抑制研究[21]。中国空气动力研究与发展中心在2.4 m跨声速风洞开展了高机动导弹的虚拟飞行试验[22]，在∅3.2 m低速风洞开展了针对固定翼飞机的虚拟飞行试验，目前试验达到的最大迎角接近30°[23]。

综上分析，风洞虚拟飞行试验技术具备多自由度、角度范围大、模型自由转动等特点，可用于飞机研制初期开展大迎角及失速尾旋特性研究。本文提出了一种大角度虚拟飞行试验装置，能够开展大迎角失速/偏离/尾旋全过程的模拟研究，可成为立式风洞尾旋试验的有力补充，可进一步完善针对尾旋问题的动态试验技术研究体系。本文采用拉格朗日乘子法建立了该装置的数学模型，结合已有风洞试验数据开展仿真研究，并与立式风洞尾旋试验结果进行对比分析，验证了该技术的可行性和应用潜力。

1 试验装置

1.1 尾旋运动特征分析

图1 稳定尾旋的受力分析Fig.1 Force analysis of steady spin

尾旋是飞机在超临界迎角范围出现绕其纵轴的自转后，在气动力、惯性力及重力的作用下，一方面绕其自身3个体轴旋转，另一方面沿半径很小的螺旋形轨迹做自发的下降运动，如图1所示。在尾旋的初始阶段，由于大迎角非对称力矩或舵面产生的偏航力矩使得飞机开始旋转；之后由于惯性耦合作用，飞机迎角进一步增大从而进入稳定尾旋状态。稳定尾旋中，重力和阻力基本平衡，升力提供向心力以维持绕铅垂轴的稳定旋转；三轴力矩基本保持平衡。在多数情况下，尾旋半径对飞机尾旋运动参数的影响较小，在一段时间内高度变化带来空气密度的影响也可忽略。因此飞机的尾旋运动可用一个动力学相似缩比模型绕一固定轴的3自由度旋转来进行模拟。比如现有的旋转天平试验、立式风洞尾旋试验等。

1.2 装置设计

本文提出的3自由度装置将在水平风洞中实现接近90°迎角的飞行动作模拟，可开展失速偏离、尾旋初始阶段和稳定尾旋的研究，如图2所示。具体的技术方案是：翼型垂直支杆通过下端安装面固定在低速风洞下洞壁或平台上。轻质曲杆一端与旋转铰联结，绕平行于风洞中心轴线自由旋转；另一端与十字万向铰固联，万向铰置于模型内部用来支撑模型，通过旋转铰和万向铰的共同作用可实现模型在俯仰、偏航、滚转3个方向较大范围内的自由转动。位于旋转铰前端的引电器用于模型内部的机载设备供电及采集机载设备的数据信号，与曲杆同步旋转，如图3所示。曲杆端部配重的高度可以手动调节，以保证曲杆的重心在曲杆的旋转轴上，保持试验旋转运动过程中实现动平衡。这样通过滚转轴和俯仰/偏航二自由度转台相结合的方式实现了试验模型物理意义明晰的3自由度运动，可实现尾旋进入、发展和改出全过程的模拟。

图2 虚拟飞行装置示意图Fig.2 Schematic of virtual flight test rig

图3 虚拟飞行装置绕速度矢滚转示意图Fig.3 Sketch of velocity-vector roll in virtual flight test rig

图4 虚拟飞行试验装置变形云图Fig.4 Strain contours of virtual flight test rig

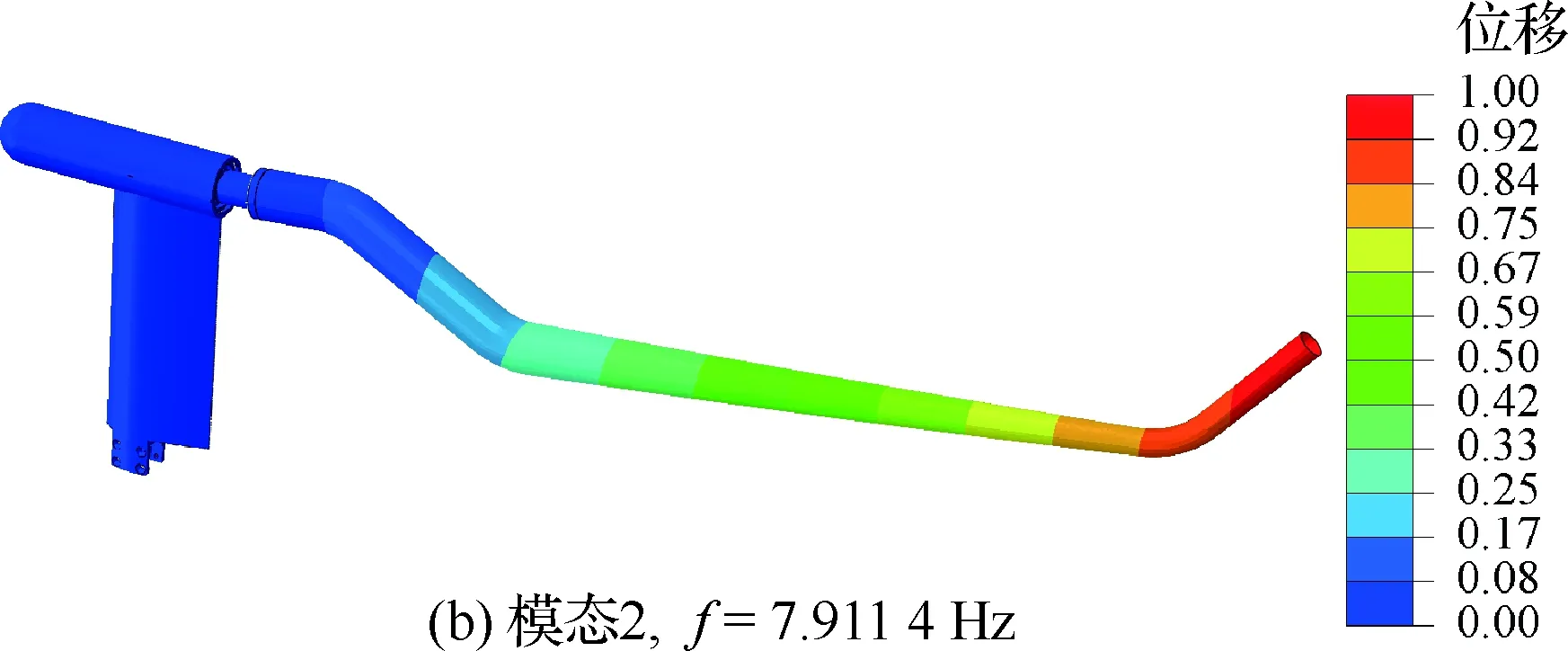
图5 虚拟飞行试验装置模态振型Fig.5 Vibration mode of virtual flight test rig

图4给出了虚拟飞行试验装置的变形云图，施加载荷为后文试验模型X、Y、Z3个方向上的最大气动载荷，此时曲杆末端的最大位移约为3.5 mm，变形量基本可以接受，后续可通过优化设计进一步提高刚度。图5给出了模态振型分析结果，其一阶固有频率f约为7.6 Hz，结合后文试验模型的动态响应特性，应可避免发生共振，图中色例描述的是归一化的位移量。

2 动力学模型

2.1 数学模型建立

2.1.1 前提和假设

风洞试验时，模型质心位于风洞试验段中心保持不变，但模型的姿态可绕三轴转动，因此，在动力学建模时可作如下假设：

1) 假设飞机模型及试验装置均为刚体，不存在变形情况。

2) 假定曲杆气动力为零，曲杆的旋转轴平行于风洞来流方向。

3) 模型的转动中心为其重心，且模型和曲杆的重心在曲杆的旋转轴上。

4) 试验模型的惯量和旋转速率较小，可忽略陀螺力矩的影响。

2.1.2 轴系及角度定义

为方便建立数学模型，本文使用如下坐标系及角度定义(见图6)：

地轴系OgXgYgZg，简称Sg，其OgZg轴沿铅垂方向向下，OgXg轴在水平面内，并与风洞轴线平行，与来流速度V方向相反，OgYg轴与平面OgXgZg垂直，指向右。

模型体轴系OaXaYaZa，简称Sa，原点为模型重心，OaXa轴在飞行器对称平面内，平行于机身轴线或机翼的平均气动弦线，指向机头；OaYa轴垂直于对称平面，指向右；OaZa轴位于对称面内，指向符合右手定则。

图6 坐标系定义Fig.6 Definition of coordinate system

曲杆体轴系OrXrYrZr，简称Sr，原点位于曲杆重心，轴系定义与Sa类似。

2.1.3 基于绝对坐标方法的动力学方程

按照绝对坐标方法，定义本系统的绝对坐标为

同时定义基于自身体轴的角速度向量ωi=[piqiri]T(i=r,a)。并有如下关系：

(1)

(2)

根据拉格朗日乘子法，给出动力学方程的一般形式为[24]

(3)

式中：λ为拉格朗日乘子；A为与无约束动力学方程有关的系数矩阵，即

(4)

其中：Ja、Jr分别为飞机模型和曲杆的惯量矩阵；Da、Dr分别为飞机模型、曲杆体轴系角速率和地轴系姿态变化率的关系矩阵。

B为该方程组右侧向量，即

(5)

(6)

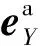
2.1.4 无违约算法

多体系统动力学建模时，常会遇到约束条件违约的问题，特别是当模型进入振荡过程中，违约现象比较明显。通常情况下这是由于动力学模型中对于约束条件的选取往往只对位移、速度、加速度中的一个量进行约束，在数值计算中不可避免地会出现其他量违背约束条件的情况。

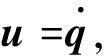
(7)

(8)

此时将速度约束表达式引入加速度约束表达式,得到

(9)

于是原动力学方程式(3)改写为

(10)

以万向铰几何约束为例，考核原动力学方程式(3)与无违约算法之间的优劣。图7是在相同条件下两种算法对万向铰两轴夹角进行复算的结果对比。如图所示，原动力学方程的结果显示万向铰两个旋转轴夹角不断扩大，与实际情况不符；采用无违约算法之后，几何违约情况基本消除，偏差值极小，修正效果好。

图7 违约修正影响Fig.7 Effect of constraint violation correction

2.2 气动力模型

本文基于常规风洞试验得到的基本气动力、舵面效率、动导数及旋转天平等数据建立了如下气动力模型，各系数均在体轴系下描述。

(FA,MA)=f(α,β,ωa,V,δe,δr,δf,δa)

(11)

式中：α为迎角；β为侧滑角；ωa为飞机的旋转角速度；δe、δr、δf、δa分别为模型升降舵、方向舵、襟翼和副翼角度，各气动系数按照基本量+增量的方式计算，即

ΔCiFO(po,qo,ro)+ΔCiRB(α,β,ωss)

i=l,m,n;j=a,e,r

(12)

式中：CiST为与迎角α、侧滑角β、襟翼δf有关的静态基本量；下标l、m、n分别表示滚转力矩、俯仰力矩和偏航力矩；ΔCiδj(δj)为舵面δj带来的增量；ΔCiFO为机体转动引起的动导数增量；ΔCiRB为机体绕速度矢旋转产生的增量；ωss为机体绕速度矢旋转的速度，即

ωss=pbcosαcosβ+qbsinβ+rbsinαcosβ

(13)

其中：pb、qb、rb为体轴系下的三轴角速率；posc、qosc、rosc用于计算动导数的振荡分量，其表达式为

(14)

2.3 摩擦力矩估算

常用的动态摩擦模型有Dahl模型、Bristle模型、Bliman-Sorine模型、LuGre模型和Leuven模型[25-26]。其中LuGre模型能精确地描述摩擦静态和动态特性，因此选择LuGre模型在稳态系统下的一种简化形式对装置中两组铰摩擦力矩进行计算，具体形式为

(15)

2.4 质心偏移影响

理想状态下，模型质心与虚拟飞行支撑装置万向铰的旋转中心应该重合。但实际上，为了保证无风条件下系统的稳定性，模型设计时质心应略低于旋转中心。另外，模型机身的高度有限，其Z向上的质心偏移较其余两个方向也不易调整。

质心偏移对试验系统带来的影响主要有3个方面：模型惯量变化、重力引起的力矩变化、气动力产生的力矩变化。对于模型惯量的变化，按照惯量平行移轴进行处理；而对于后两者，将重力、气动力在模型体轴系表述后，与偏移向量叉乘可得到力矩的变化量，具体为

MG=rcg×G

(16)

MFA=rcg×FA

(17)

式中：MG、MFA分别为重力和气动力产生的力矩；rcg为质心偏移向量；G、FA分别为重力和气动力。

3 仿真与尾旋试验方法

3.1 仿真程序

仿真程序在MATLAB环境下编写，采用Nelder-Mead算法在给定初始状态下配平飞机；导出约束方程的Jacobian矩阵的解析形式，与无约束的动力学方程联立构成动力学模型，然后采用无违约算法进行求解。图8给出了仿真程序的相关模块和主要流程。

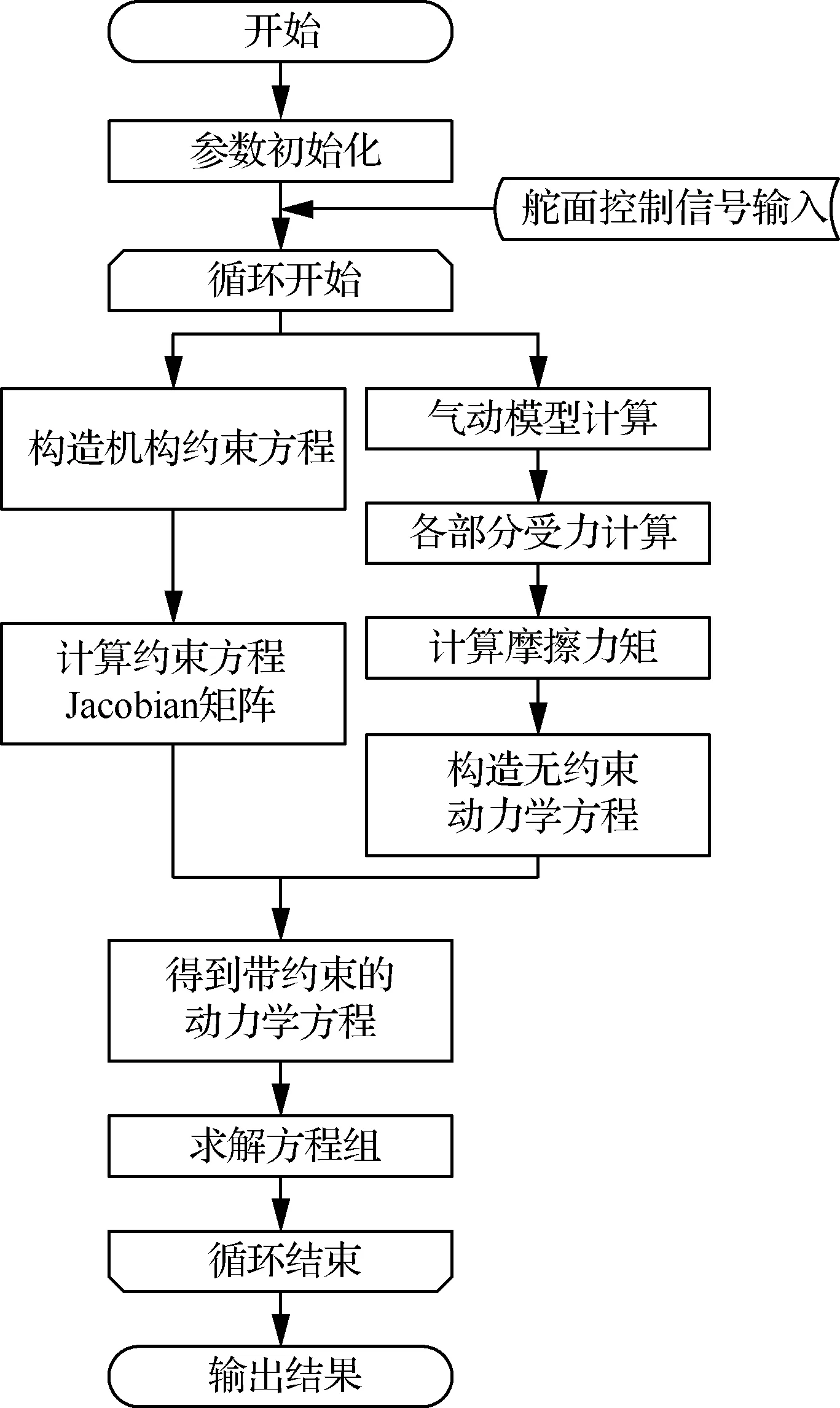
图8 仿真流程Fig.8 Flow chart of simulation

3.2 立式风洞尾旋试验

图9 立式风洞尾旋试验场景Fig.9 Scene of spin test in vertical wind tunnel

为了验证该方案的可行性，将仿真结果与立式风洞试验结果进行对比分析。∅5 m立式风洞是国内唯一一座研究飞机尾旋运动的特种风洞。尾旋试验模型除与真实飞行器保持几何相似外，还需要满足动力学相似准则，主要是满足弗劳德数相似[27-28]。立式风洞采用吊挂支持模型法进行飞机尾旋研究试验。试验中，飞机模型被两根绳索悬挂在风洞试验段中，如图9所示。在试验段气流较低时，模型投手将模型按预定的姿态(模型迎角大于失速迎角)投入试验段中心区域垂直上升的气流中，同时给模型施加一个初始旋转速度(约1～3圈/s)，然后逐步增加试验段风速到某个值使得模型平衡于风洞中心区域并进入尾旋状态(平衡灯亮)，尾旋运动测量系统开始记录模型做尾旋运动时各运动参数随时间的变化规律。模型尾旋运动参数由微型姿态航向参考系统(Attitude Head Reference System, AHRS)获得，AHRS内部集成了基于MEMS(Micro ElectroMechanical Systems)技术的三轴陀螺仪、加速度计及磁强计，其内部包含了嵌入式的姿态数据解算单元，通过Kalman滤波的方法，给出模型姿态角、角速度、加速度等测量信息。

3.3 仿真与试验条件

本文以某飞机为例，按照相同的进入舵偏、止旋舵偏、低头舵偏开展研究，仿真中飞机模型的主要参数与立式风洞尾旋试验的模型参数保持一致，具体见表1。

首先通过与立式风洞尾旋试验结果、6自由度动力学方程仿真结果进行对比，验证3自由度虚拟飞行试验装置数学模型的正确性和合理性。仿真与试验的舵面控制信号均为：进入尾旋阶段，1 s时升降舵为-5°，2.5 s时升降舵回零，副翼为30°；改出尾旋阶段，18.4 s时使副翼偏转到-30°，1 s后副翼回零，升降舵为30°。

在此基础上，进一步分析了该装置中曲杆惯量、摩擦力矩以及模型质心偏移等因素对结果的影响，给出设计机构和开展试验的建议。此时的控制信号仅保留上述进入尾旋阶段的信号。

表1 试验模型主要参数Table 1 Major parameters of test model

4 结果分析

4.1 与立式风洞尾旋试验结果对比

如图10所示，图中3组曲线分别是6自由度仿真计算结果、3自由度曲杆虚拟飞行装置无摩擦仿真结果(图中标注为“带曲杆仿真”)和立式风洞尾旋试验结果。由于立式风洞尾旋试验不能模拟尾旋进入阶段，因此，该曲线仅有稳定尾旋及改出阶段。6自由度和3自由度虚拟飞行的结果总体一致性较好，主要区别在于尾旋进入阶段，前者的俯仰振荡较后者剧烈一些，这可能与3自由度虚拟飞行装置的位移约束有关。

从迎角响应可以看出，尾旋稳定阶段三者的平均迎角均在82°左右，振荡周期接近，其中3自由度虚拟飞行的结果略大。3者的振荡谷值比较接近，但两组仿真数据曲线比试验结果振幅小。采用同样的止旋操作、低头操作后，数据响应总体趋势一致，3种状态均能达到改出效果。同时注意到，尾旋试验中迎角低于60°后不再下降，这与尾旋试验时一旦改出尾旋状态后模型迅速脱离流场区域以及上下吊索的拖拽有关。从侧滑角响应看出，3者的平均侧滑角均在7°左右，振荡周期3者接近，两组仿真结果的振幅同样比试验结果小，改出过程趋势基本一致。

6自由度和3自由度的仿真结果与立式风洞试验结果在迎角、侧滑角振荡幅值等方面的差异，一方面与仿真中使用的静态测力、动导数及旋转天平等风洞试验数据的系统误差、动态试验数据使用方法有关，试验误差包括洞壁干扰、支架干扰、雷诺数效应等；另一方面与立式风洞尾旋试验的误差有关，包括数据精度、上下吊索干扰、模型可能存在竖向的重心偏移等因素。

从三轴角速度响应看出，仿真数据与试验数据的均值接近，俯仰和滚转振荡幅值较小，改出阶段响应趋势一致。3组结果的绕速度矢滚转速率比较接近，其中3自由度虚拟飞行的结果略小，改出过程变化趋势基本一致。

此外，虚拟飞行试验中，由于风速始终保持水平方向，模型绕速度矢滚转时模型俯仰姿态呈正弦振荡形式，但基本不影响气动力。3者稳定尾旋状态的下沉速度基本一致。

综合以上对比分析认为，3自由度虚拟飞行试验装置可以模拟飞机尾旋进入、发展和改出的全过程；与立式风洞试验结果对比表明，该技术可以捕获尾旋发展和改出阶段的主要特征参数，为风洞中研究大迎角失速/尾旋问题提供新的解决途径。

图10 仿真结果与垂直风洞试验数据对比Fig.10 Comparison of results of simulation and vertical wind tunnel test

4.2 旋转曲杆的影响

3自由度虚拟飞行试验装置中模型的滚转运动通过曲杆和模型的同步旋转实现，因此曲杆的存在对模型的运动会有一定的影响。由于曲杆只有一个转动自由度，其绕自身X轴的惯量是影响模型尾旋运动的主要因素。

图11给出了无摩擦状态下不同曲杆惯量的仿真结果。本文中默认的曲杆惯量占飞机模型滚转惯量的10%，以此为基准，分别减小和增大50%，得到3组不同惯量下的结果。从图中可以发现，模型经过一段时间的大幅振荡后才进入稳定尾旋状态，而随着曲杆惯量增大，进入阶段的时间明显增加，幅值有所增大，但振荡周期基本不变。进入稳定尾旋后，迎角、侧滑角振荡的幅值随着曲杆惯量的增加略有增长，振荡均值基本不变，振荡周期基本也不变；角速率方面受曲杆惯量的影响与之类似，振荡幅值增加、均值和周期基本不变，绕速度矢滚转速率基本不变。因此曲杆对稳定尾旋影响有限，但对进入阶段有一定影响。

通过对迎角、侧滑角稳定振荡的部分进行快速傅里叶变换(FFT)并绘制频谱(见图12)后发现，模型迎角、侧滑角振荡存在两个主要频率，分别为1.1 Hz和1.35 Hz，其中后者与尾旋自由飞时模型振荡频率一致，因此前者应为支撑机构带来的影响。此时两个频率相近的低频信号互相叠加，引发拍现象，使得动态响应曲线的振荡幅值忽大忽小。

图11 不同杆惯量仿真结果Fig.11 Results of simulation with different inertia of rod

图12 不同杆惯量仿真结果的幅频图Fig.12 Amplitude-frequency diagram of results of simulation with different inertia of rod

从频谱图亦可看出，随曲杆惯量增长，3组数据的频率基本不变。这是由于稳定尾旋发生在模型迎角82°附近，此时将曲杆惯量投影到模型体轴系后发现，曲杆惯量分解到模型偏航轴的部分占主量；而模型偏航惯量近似为滚转惯量的8倍，经过测算，曲杆惯量的变化使系统在模型滚转方向的惯量变化约为7‰，在偏航方向的惯量变化约为5‰，因此对振荡频率影响较小。

曲杆加工完成后，曲杆惯量基本不变。因此，为了更好地模拟真实尾旋运动的信息，机构设计时应严格控制曲杆惯量，如通过材料和工艺的选取以严格控制曲杆惯量所占模型的惯量比重。根据仿真结果，建议将曲杆和模型的滚转惯量比值控制在10%以内。

4.3 摩擦力的影响

3自由度虚拟飞行试验装置中存在3个自由旋转铰，每个铰联接副之间存在固有的摩擦力矩。仿真分析了无摩擦、1倍摩擦和2倍摩擦力矩对尾旋试验结果的影响，具体的对比结果见图13。从图中可以发现，不同摩擦力矩下模型在尾旋进入和稳定阶段响应形态一致，摩擦力矩的影响并不明显。

图13 不同摩擦力矩仿真结果Fig.13 Simulation results with different friction moments

4.4 质心偏移的影响

对于动力学相似缩比模型，模型质心的Z方向位置一般不易调整；而且模型安装时也可能会出现模型质心与万向铰旋转中心有偏差的情况。因此通过设置模型质心在Z轴方向上与万向铰旋转中心的偏移量来进行仿真，以分析质心偏移带来的影响。

如图14所示，模型重心与万向铰旋转中心不重合时，在初始配平舵偏下模型不再平衡，略有低头；给定舵面操纵信号后，仍能进入尾旋，但随着偏移量增大，各状态量的振荡幅值相应增大，重心偏移0、3、5 mm情况下，迎角振荡幅值分别为4°、10°、16°，侧滑角振荡幅值分别为5°、11°、18°；均值基本不变，振荡周期略微增加。

图14 不同质心偏移仿真结果Fig.14 Results of simulation with different offsets of center of mass

5 结 论

基于低速风洞3自由度虚拟飞行试验装置进行了某典型飞机尾旋的建模和仿真研究。

1) 该装置可在水平风洞实现飞机尾旋的进入、发展和改出各阶段的模拟，其中稳定尾旋的运动参数及模型姿态与立式风洞尾旋试验结果较为吻合，可作为飞机尾旋风洞试验研究的有力补充。

2) 曲杆惯量不影响模型尾旋运动的振荡均值、旋转速率等特征参数，但会延长模型进入尾旋过程，影响尾旋特征参数的振荡幅值。建议将曲杆和模型的滚转惯量比值控制在10%以内。

3) 摩擦力矩在一定范围内对模型尾旋运动的主要特征参数没有明显影响。

4) 质心偏移会影响模型尾旋运动的振荡幅值，对均值、旋转速率影响不大。建议控制模型重心与万向铰旋转中心的偏移量在3 mm以内。