高超声速飞行器宽速域翼型/机翼设计与分析

孙祥程，韩忠华，柳斐，宋科，宋文萍

西北工业大学 航空学院 翼型叶栅空气动力学国家级重点实验室，西安 710072

随着空间探索与空间应用等活动的日益频繁，各种航天运输任务的需求日趋迫切，人类需要更加快速、机动性更强、廉价和安全可靠的能进行天地往返运输的高超声速飞行器。高超声速飞行器正向着速域更宽、空域更广、航程更远的方向发展[1-2]。这就要求高超声速飞行器需要从地面起飞，经历低速、跨声速、超声速，直至高超声速巡航等多个飞行阶段。因此，除了需要保证高超声速性能外，对于高超声速飞行器还必须兼备满足工程需求的亚跨超声速特性。但是各个速度阶段的气动性能所要求的气动外形/构型往往是相互矛盾的。因此，亟需开展考虑低速以及跨、超和高超声速特性的翼型/机翼综合优化设计研究。

传统的高超声速翼面/舵面大多直接采用四边形、六边形等外形简单的翼型。但这些翼型仅能满足超声速和高超声速气动特性的需求，无法兼顾低速和跨声速的气动特性。因此，合理的翼型设计，对解决高超声速飞行器宽速域气动特性兼顾的问题具有重要意义。

国内外关于高超声速翼型的气动特性研究及气动优化设计方面的文献比较少。其原因在于高超声速条件下，翼型的作用相比于亚跨声速明显减弱。随着高超声速飞行器对宽速域气动性能的需求，翼型的研究又逐渐得到国内外研究者的重视。西北工业大学曹长强等[3]开展了超声速多边形翼型和双弧形翼型气动优化设计研究，但没有考虑超声速翼型的跨声速气动特性。Ueno和Suzuki[4]对高超声速翼型进行了优化设计，在保证高超声速高升阻比的同时，考虑了跨声速的气动性能。

本文利用课题组自主开发的雷诺平均Navier-Stokes(RANS)方程流场求解器程序PMNS2D[5-6]，结合基于代理模型的多目标多约束高效通用优化软件“SurroOpt”[7-9]，以NACA64A-204为基准翼型，开展了高超声速飞行器宽速域翼型的气动优化设计研究，设计了一种能够兼顾宽速域气动特性的翼型。并将该翼型配置在空天飞机机翼上，实现了良好的宽速域气动特性。

1 流动数值模拟方法

采用课题组自主开发的RANS方程流场求解器PMNS2D进行数值模拟。在连续介质假设下，惯性坐标系下忽略体积力和热源的二维非定常可压缩雷诺平均Navier-Stokes方程可写为

(1)

式中：W为流动守恒变量；H为无黏通量；Hv为黏性通量；Ω为控制体；∂Ω为控制体边界；n为任意控制体边界∂Ω的单位外法向量；S为控制体边界的面积。

本文采用格心有限体积法在结构化网格上求解式(1)，时间推进采用隐式LU-SGS格式，模型采用一方程Spalart-Allmaras[10]湍流模型实现控制方程的封闭。跨声速状态下，空间离散采用中心格式，高超声速状态下采用高阶迎风AUSM+_up格式[11]。

2 优化设计方法

2.1 CST几何外形参数化方法

美国波音公司的Kulfan[12-13]等提出了一种基于型函数/类函数变换(Class function/Shape function Transformation, CST)的参数化方法。该方法参数具有明确的几何意义，控制参数少，适应性强，精度好。

采用CST函数方法对翼型进行参数化的表达式为

上表面：yu=C(x)·Su(x)+x·yTEu

下表面：yl=C(x)·Sl(x)+x·yTEl

式中：C(x)为类函数；S(x)为型函数；yTEu、yTEl分别为上下表面后缘的y坐标，下标“u”和“l”分别表示上下表面。

本文采用的是8阶CST参数化方法，共18个设计变量。

2.2 代理优化方法

采用课题组自主开发的基于代理模型的多目标多约束高效通用优化程序“SurroOpt”[7-8]，其设计流程如图1所示。首先，通过试验设计(DoE)在设计空间上选取少量的样本点，对其进行高可信度分析计算；其次，用所获得的样本数据集建立一个真实目标函数的替代模型；然后，根据一定的加点准则，如EI(Expected Improvement)和MSP (Minimum of Surrogate Prediction)指导新样本点的加入，不断更新模型，从而使新产生的样本点序列不断逼近全局或局部最优解。

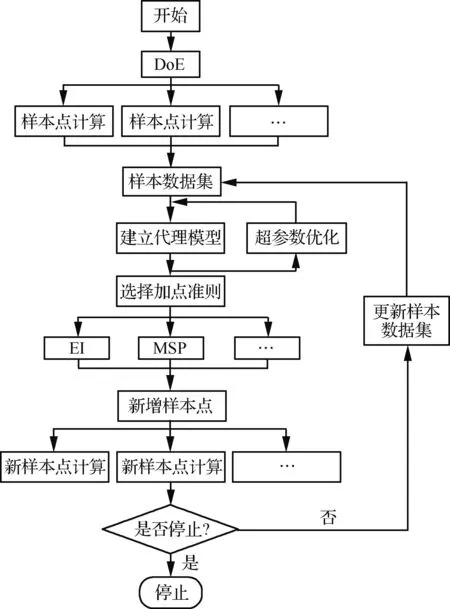
图1 基于代理模型的优化方法流程Fig.1 Flowchart of surrogate-based optimization method

3 宽速域翼型优化设计

3.1 数值模拟程序有效性验证

对RAE2822翼型在跨声速状态下进行翼型绕流计算，计算网格如图2所示，计算状态为马赫数Ma=0.734,迎角α=2.79°,雷诺数Re=6.5×106。图3中试验数据来自文献[14]。根据图3可以看出计算压力系数Cp分布与试验结果吻合较好。表1对比了试验值与 PMNS2D求解器计算所得的力系数，可以看出，数值模拟得出的阻力系数稍微偏大，而升力系数则十分接近试验值。

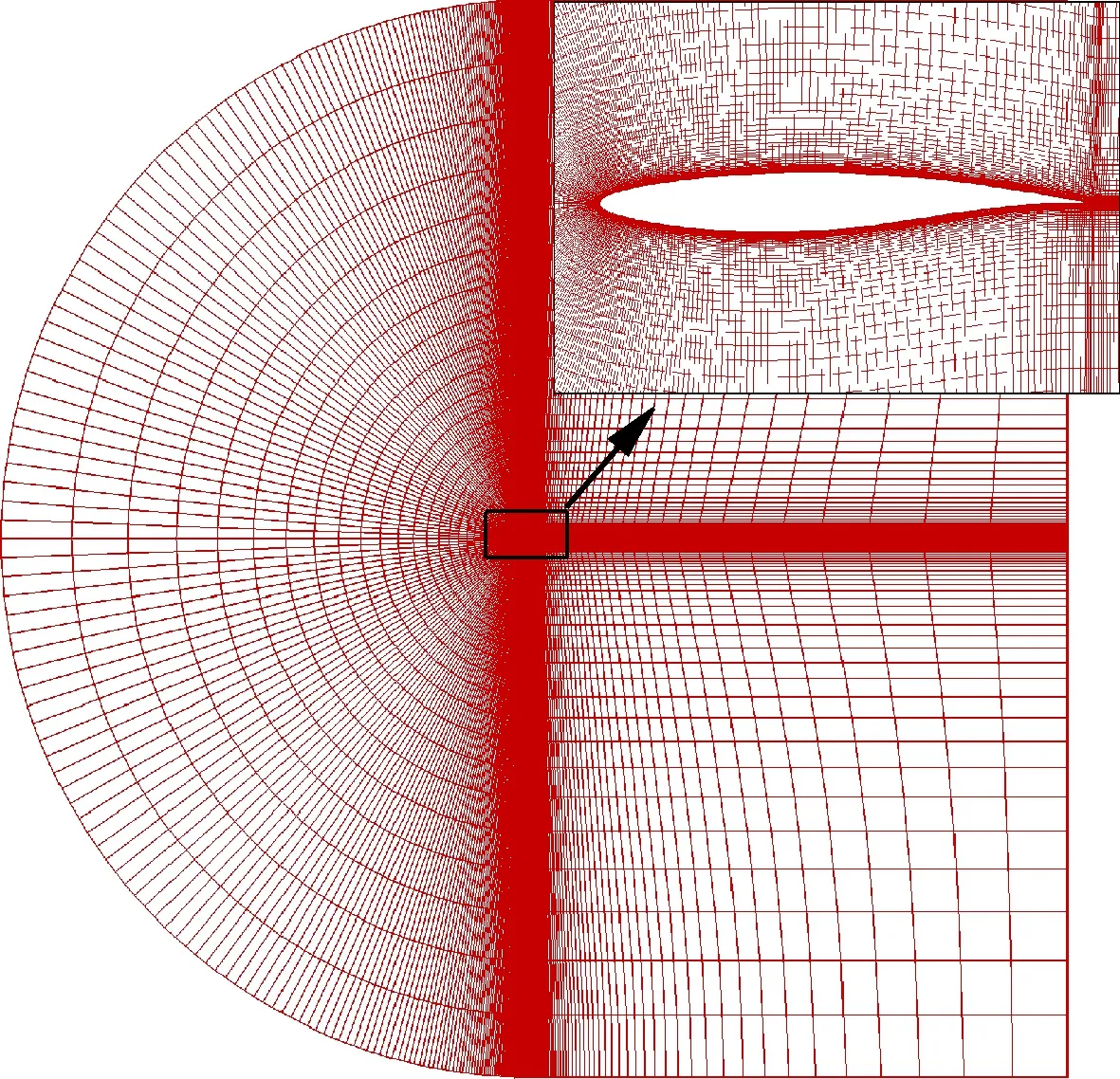
图2 RAE2822翼型计算网格示意图(417×129)Fig.2 Schematic of computational grid for RAE2822 airfoil (417×129)

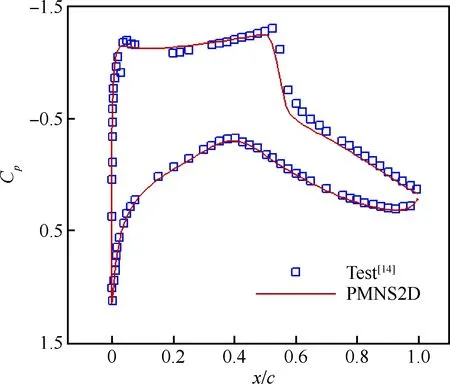
图3 RAE2822翼型计算压力分布与试验值对比Fig.3 Comparison of computed pressure distribution and experimental data for RAE2822 airfoil

对方形弹体进行高超声速状态下的数值计算，图4为方形导弹网格示意图，第1层网格高度为7.0×10-6m，网格量约为250万。图5为在Ma=4.5 、Re=1.312×107、滚转角γ=0°状态下，方形导弹气动力计算结果与试验值的对比，其中，试验数据和几何参数均来自文献[15]。图中：Cn、CA和Cm分别为法向力系数、轴向力系数和俯仰力矩系数。由图5知，法向力系数Cn与俯仰力矩系数Cm的计算结果与试验值吻合较好，轴向力系数CA计算结果与试验值变化趋势相同，但是较试验值有所增大，这主要是因为试验是在自由转捩条件下进行的，而计算采用的是全湍流模型。经过算例验证，证明本文采用的数值计算方法可靠。

表1RAE2822翼型气动力系数计算结果与试验值对比

Table1ComparisonofcomputedaerodynamiccoefficientsandtestdataforRAE2822airfoil

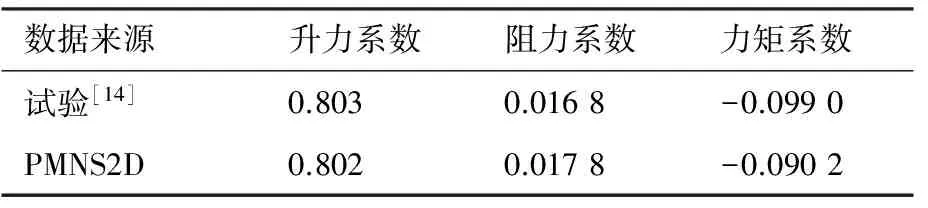
数据来源升力系数阻力系数力矩系数试验[14]0．8030．0168-0．0990PMNS2D0．8020．0178-0．0902

图4 方形截面导弹计算网格示意图(网格量约250万)Fig.4 Schematic of computational grid for square section missile (2.5 million grid points)

图5 方形截面导弹气动力系数计算值与试验值对比 (Ma=4.5, Re=1.312×107, γ=0°)Fig.5 Comparison of computed aerodynamic coefficients and test data for square section missile(Ma=4.5, Re=1.312×107, γ=0°)

3.2 翼型优化设计

以NACA64A-204翼型为基准翼型，以高超声速下的升阻比为优化目标，将跨声速时的升阻比作为约束，开展高超声速飞行器宽速域翼型单目标气动优化设计。跨声速设计状态：高度9 km，马赫数0.8，雷诺数7.6×106，迎角1.5°；高超声速设计状态：高度26 km，马赫数6，雷诺数4.23×106,迎角5°。

优化问题的数学模型为

maxKMa=6

(2)

式中：KMa=0.8和KMa=6分别为优化翼型在跨声速和高超声速下的升阻比；CL,Ma=6为优化翼型在高超声速下的升力系数；CL,Ma=0.8为优化翼型在跨声速下的升力系数；t为优化翼型的厚度,下标“0”为基准翼型。

跨声速状态下的力矩参考点取在距离翼型前缘25%弦长处，高超声速状态下的力矩参考点取在距离翼型前缘50%弦长处；前缘半径不小于0.1%弦长；翼型厚度在4%±0.02%弦长范围内。翼型外形的变形采用2.1节所提到的8阶CST参数化方法。在开始优化之前，采用拉丁超立方抽样生成20个初始样本点，优化过程中通过EI+MSP加点准则[7-8]每次增加2个点。EI+MSP加点准则是一种高效全局的组合加点方法，该方法将全局的EI加点准则和局部的MSP加点准则结合，在一次加点过程中同时将两种方法搜索到的点加入样本点集中，既提高了代理优化的效率又能保证优化的全局性。

图6 跨声速状态计算网格示意图(417×129)Fig.6 Schematic of computational grid for transonic flows (417×129)

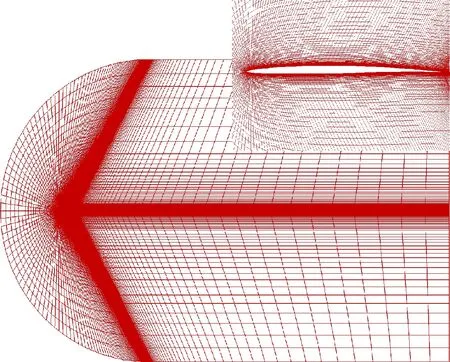
图7 高超声速状态计算网格示意图(385×129)Fig.7 Schematic of computational grid for hypersonic flows (385×129)

利用课题组自主开发的网格生成程序进行网格生成，网格如图6和图7所示。跨声速时采用C型网格，远场为150倍弦长，第1层网格高度为10-5，网格量为3.3万；高超声速时采用C型网格，前部远场距离为10倍弦长，后部远程距离为20倍弦长，第1层网格高度为10-5，网格量为5.0万。为了更精确地计算激波区域，先通过常规网格求解出激波的大致位置，然后进行加密处理。

图8为经过两轮优化的收敛曲线，纵坐标为优化目标值，即高超声速下的升阻比。因为优化的翼型前缘半径太小，所以通过修形来保证前缘半径为0.1%弦长。图9为基准翼型与修形后优化翼型的几何外形对比。其最大厚度位置接近于50%处较基准翼型靠后，上表面过渡平滑，下表面具有特殊的双“S”构型。图10为基准翼型与修形后优化翼型的压力系数分布对比。可以看出，优化后翼型上表面压力梯度变小，降低了波阻，并且其下表面的双“S”型外形在前部产生等熵压缩，后部进行二次压缩提供了一定的升力，保证其在跨声速下具有良好的升阻特性。在高超声速下，优化翼型通过下表面的前后加载提供了额外的升力，使其在高超声速下同样具有较好的升阻特性。

对基准翼型和优化翼型在跨声速和高超声速状态下进行数值求解，表2为两个状态的气动力系数对比。其中跨声速下的升力系数作为约束条件还没到边界，还具有优化空间。可以看出，与基准翼型相比，优化翼型在跨声速下的升阻比增加了15.93%，在高超声速下的升阻比增加了121.64%，高超声速的气动性能增加明显。

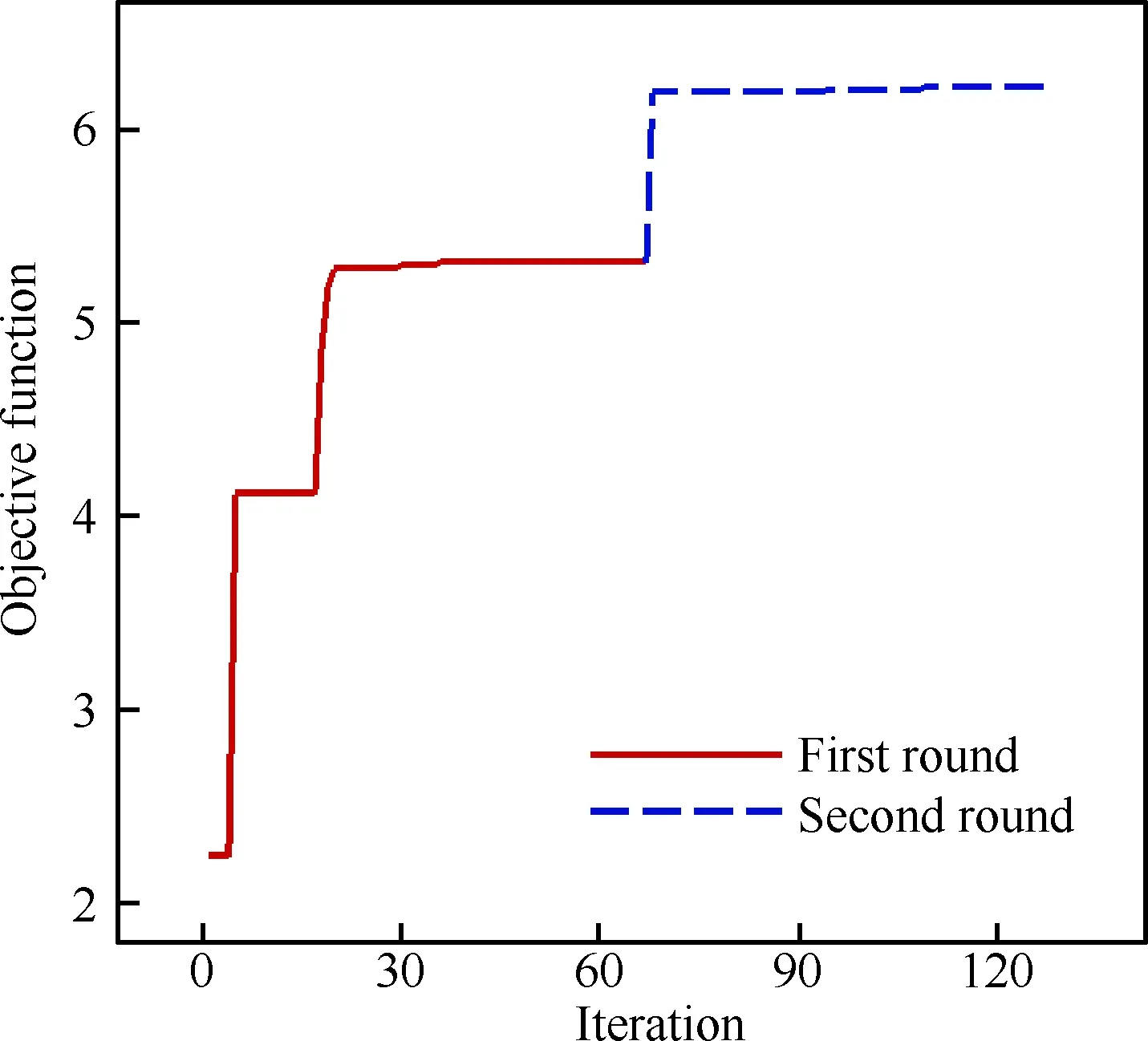
图8 目标函数收敛曲线Fig.8 Convergence history of objective function

图9 基准翼型与优化翼型几何外形对比Fig.9 Comparison of geometric shapes of baseline and optimized airfoils

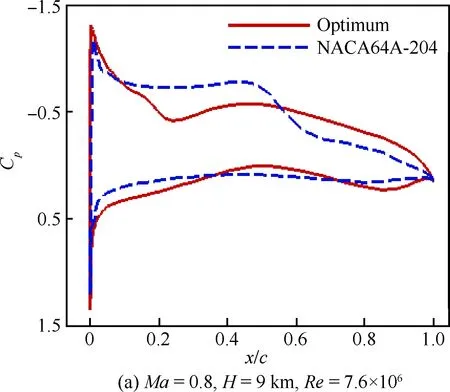
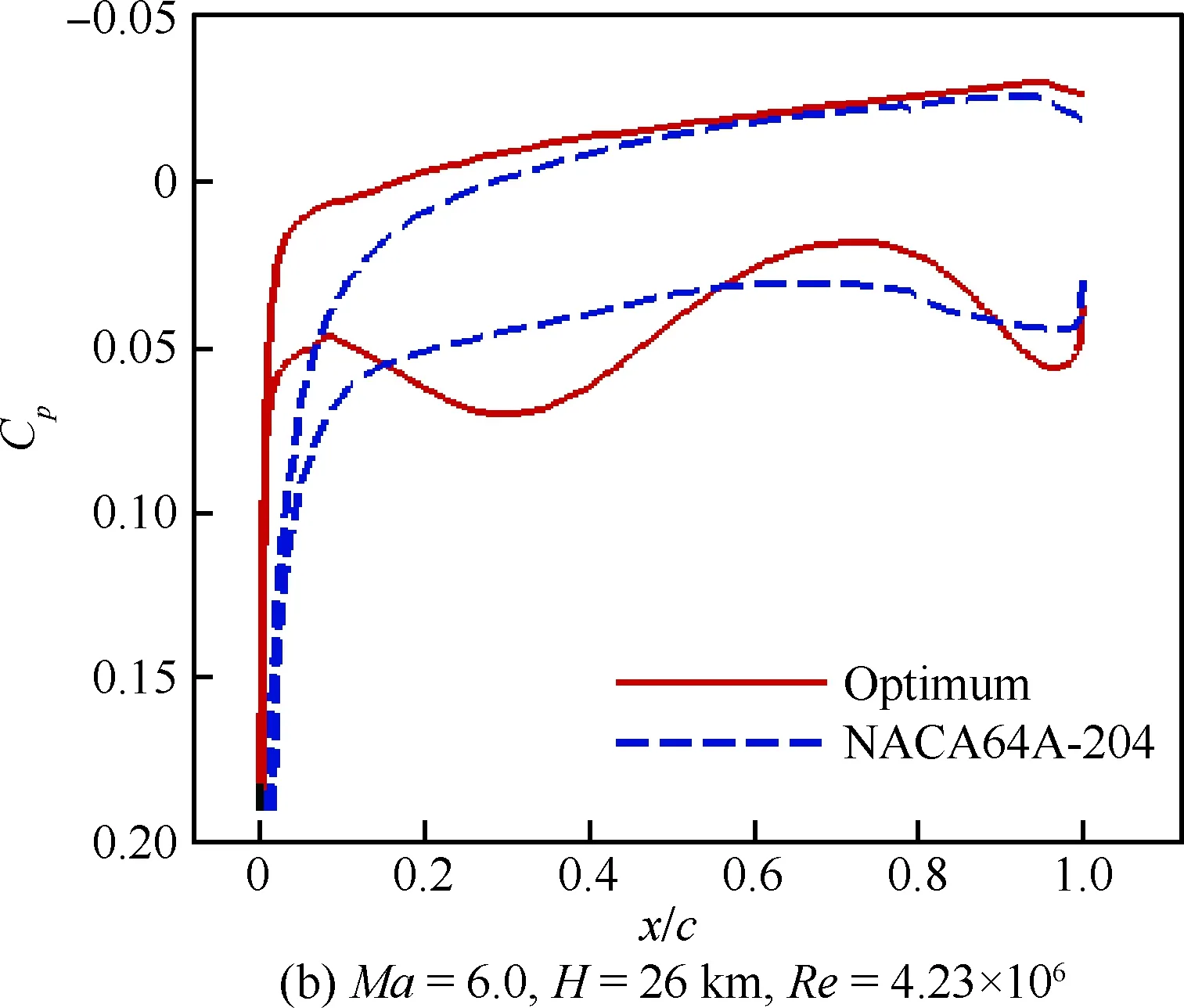
图10 优化翼型与基准翼型压力系数分布对比Fig.10 Comparison of pressure coefficient distributions between baseline and optimized airfoils

表2 优化翼型与基准翼型的气动力系数对比Table 2 Comparison of aerodynamic coefficients for optimized and baseline airfoils

3.3 优化翼型综合评估

为了验证该优化翼型相比于常规的高超声速翼型，在跨声速和高超声速下具有更加优良的气动特性，本文将该优化翼型与上下对称的四边形、六边形翼型的气动力系数进行对比分析。

选取的四边形、六边形翼型外形示意图如图11所示。其中，四边形翼型的厚度为4%弦长，最大厚度位置为50%弦长处，前倒圆半径r为0.1%弦长。选取的六边形翼型的翼型厚度为4%弦长，靠前缘的最大厚度位置为25%弦长处，靠后缘的最大厚度位置为75%弦长处，前倒圆半径r为0.1%弦长。

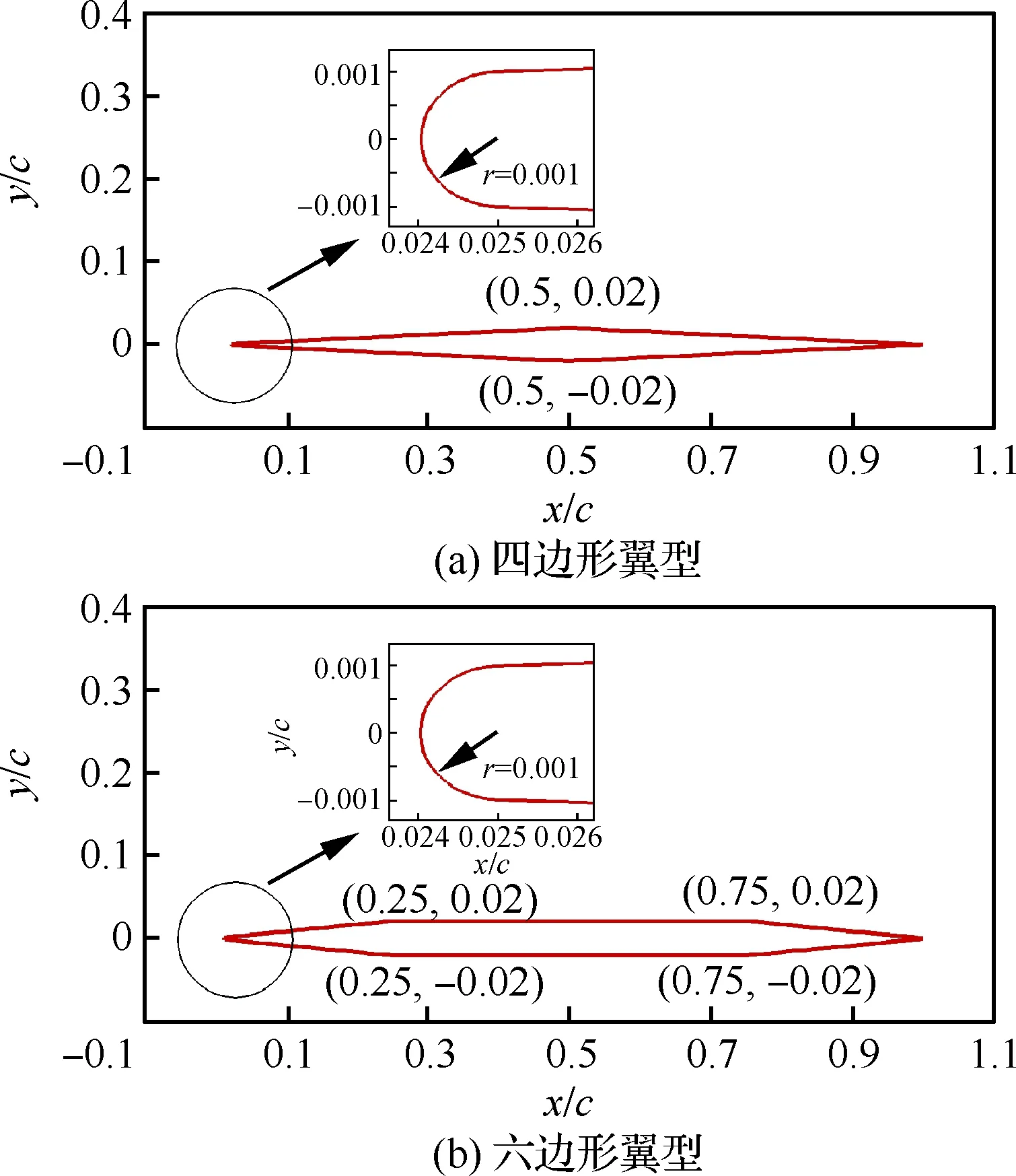
图11 典型高超声速翼型外形Fig.11 Typical hypersonic airfoils shape

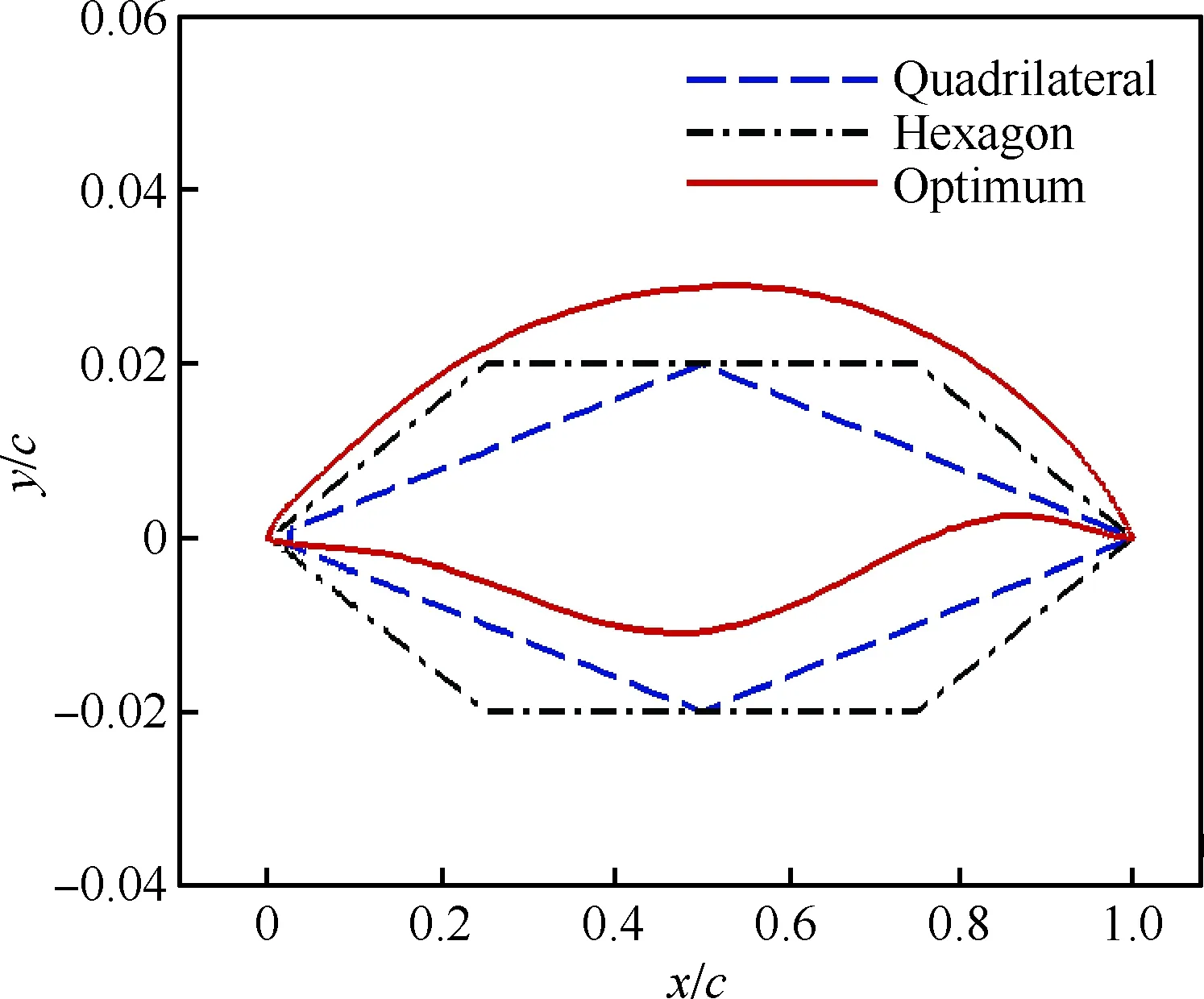
图12 优化翼型与传统高超声速翼型几何外形对比Fig.12 Comparison of airfoil geometries between optimized airfoil and conventional hypersonic airfoils

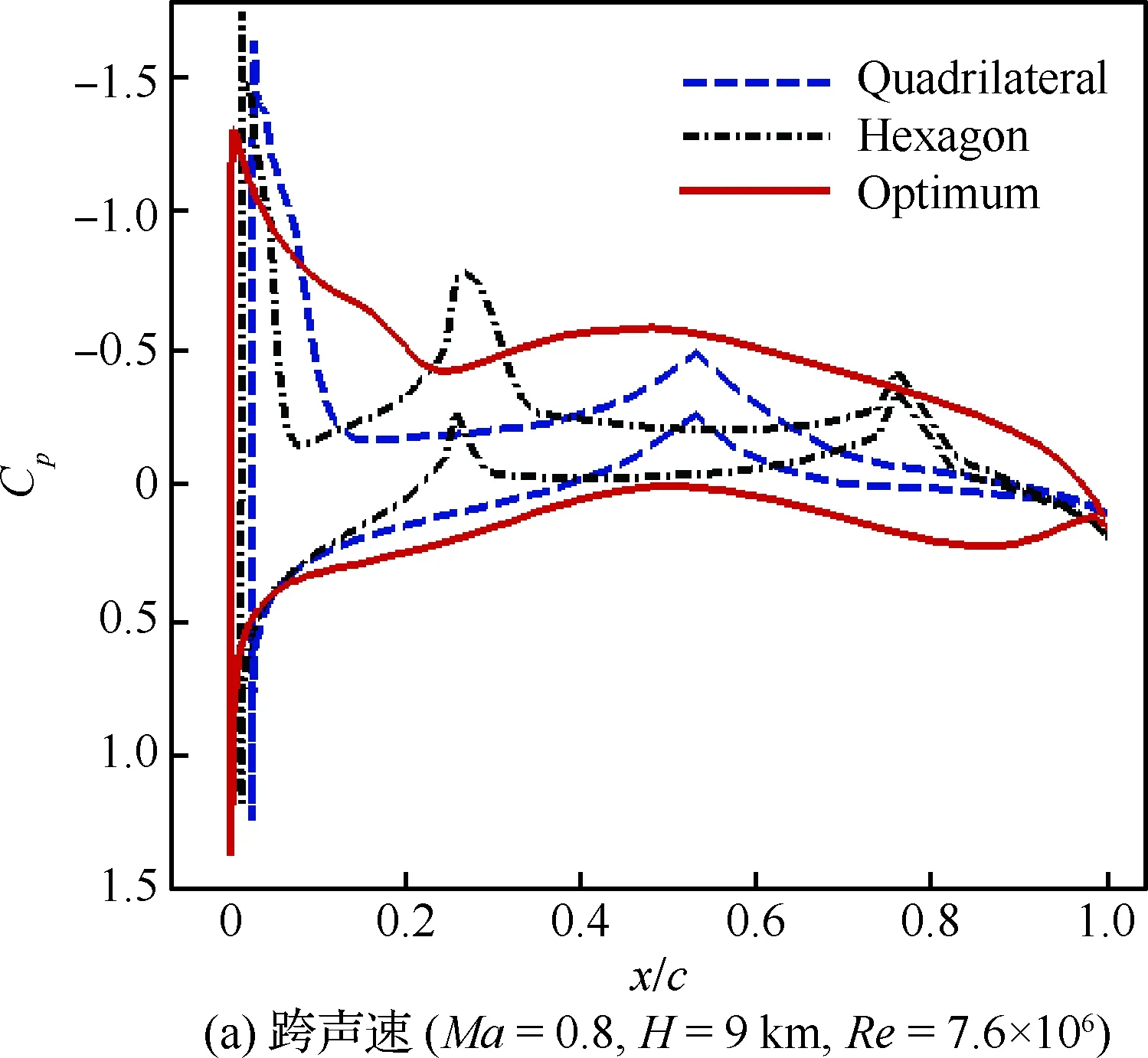
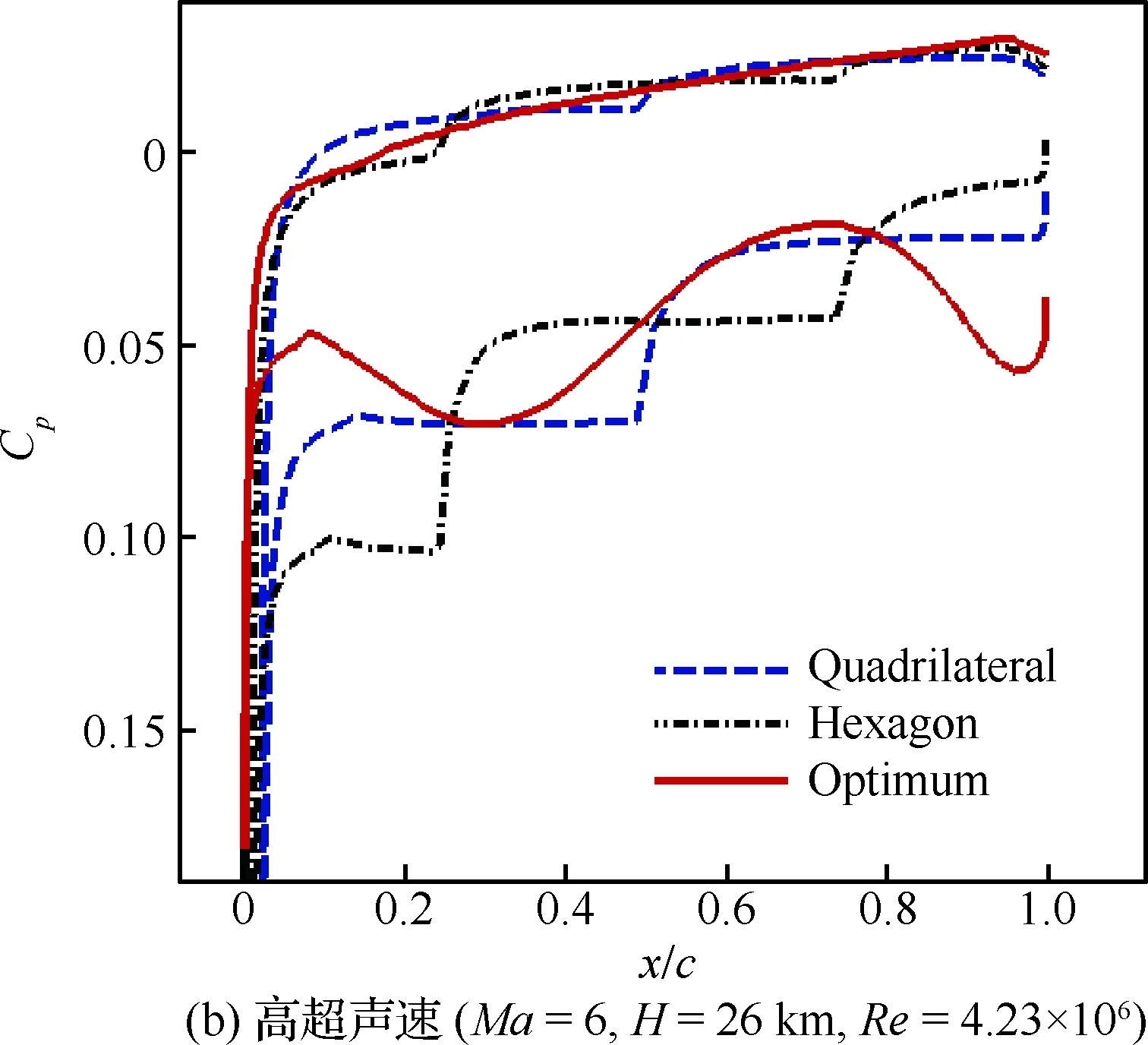
图13 优化翼型与传统高超声速翼型压力系数分布对比Fig.13 Comparison of pressure coefficient distributions between optimized airfoil and conventional hypersonic airfoil

通过几何外形和压力分布对比图(图12和图13)可以看到，优化翼型通过其下表面独特的双“S”型外形，使其在跨声速和高超声速下能在下表面产生前后加载，提供额外的升力，其上表面过渡平滑，在跨声速时有较低的压力梯度。结合3种翼型在跨声速和高超声速状态下的马赫数云图(图14和图15)可以看到，在跨声速状态下，优化翼型的前缘上表面20%处产生了一道弱激波，激波阻力降低，低压区明显，后缘下表面产生了高压区，能够提供一定的升力。在高超声速计算状态下，优化翼型的上表面马赫数梯度较小过渡平滑，下表面靠后缘处有明显的高压区，能对升力进行补偿。

图16和图17分别为跨声速和高超声速状态下的气动力系数对比。可以明显看出在跨声速状态下，优化翼型的升力系数和升阻比都远大于四边形和六边形翼型，优势非常明显，力矩系数有所增大，在设计点的俯仰力矩系数绝对值在0.1以内(设计点力矩系数为-0.088 4)，力矩特性与目前实际使用的超临界翼型相当，由此带来的配平阻力也较小；在高超声速状态下，优化翼型升阻比与四边形翼型和菱形翼型相当或略高，力矩特性与四边形相近。为了全面验证优化翼型的宽速域升阻特性， 在表3中补充了低速状态 (Ma=0.2,α=8.0°)和超声速状态(Ma=1.5,α=4.0°)的气动力数据。可以看出，除了在超声速时升阻比略低于四边形，优化翼型的升阻特性在宽速域范围内都较传统高超声速翼型更优。

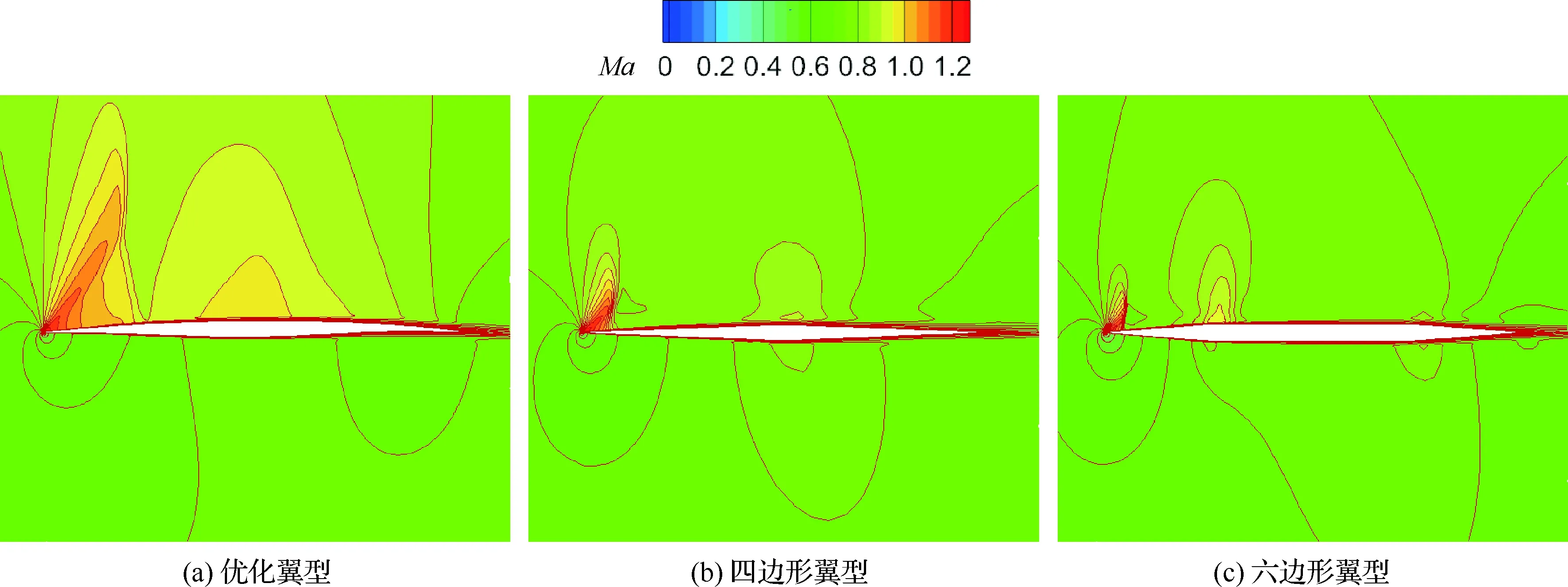
图14 跨声速状态下优化翼型与传统高超声速翼型的马赫数云图对比(Ma=0.8, α=1.5°)Fig.14 Comparison of Mach number contours of optimized airfoil and conventional hypersonic airfoil in transonic flow (Ma=0.8, α=1.5°)

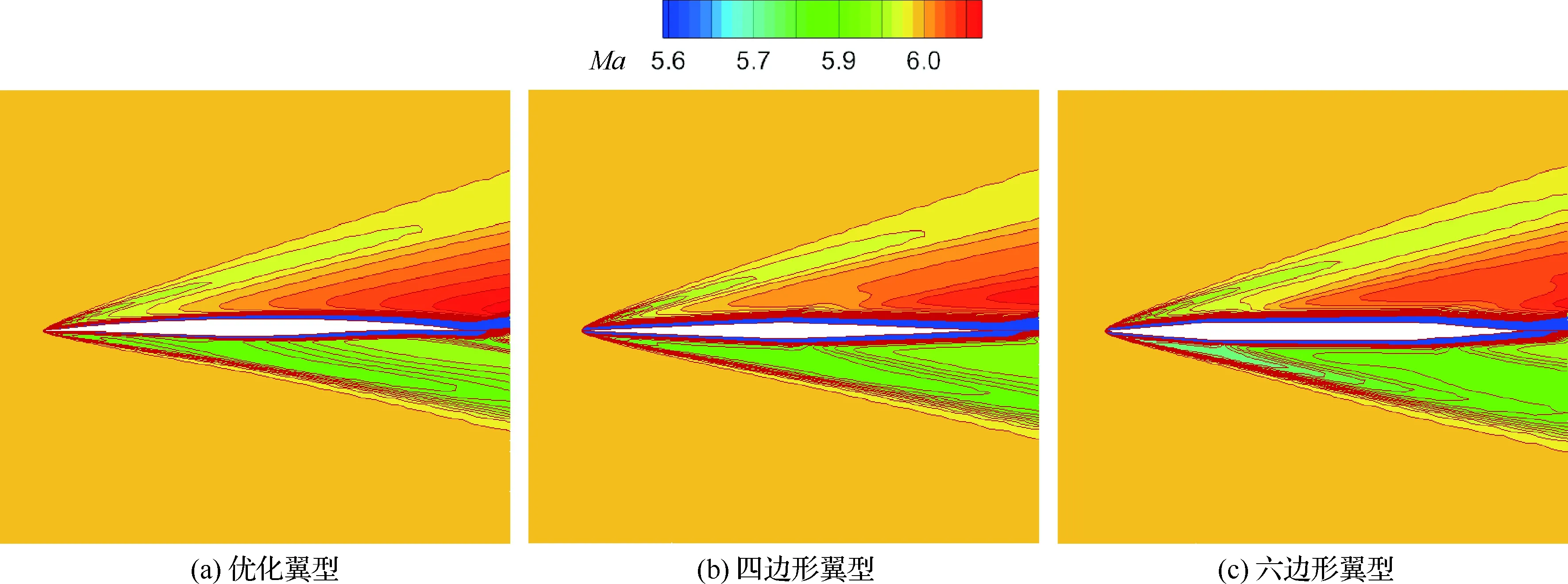
图15 高超声速状态下优化翼型与传统高超声速翼型的马赫数云图对比 (Ma=6, α=5.0°)Fig.15 Comparison of Mach number contours of optimized airfoil and conventional hypersonic airfoil in hypersonic flow (Ma=6, α=5.0°)

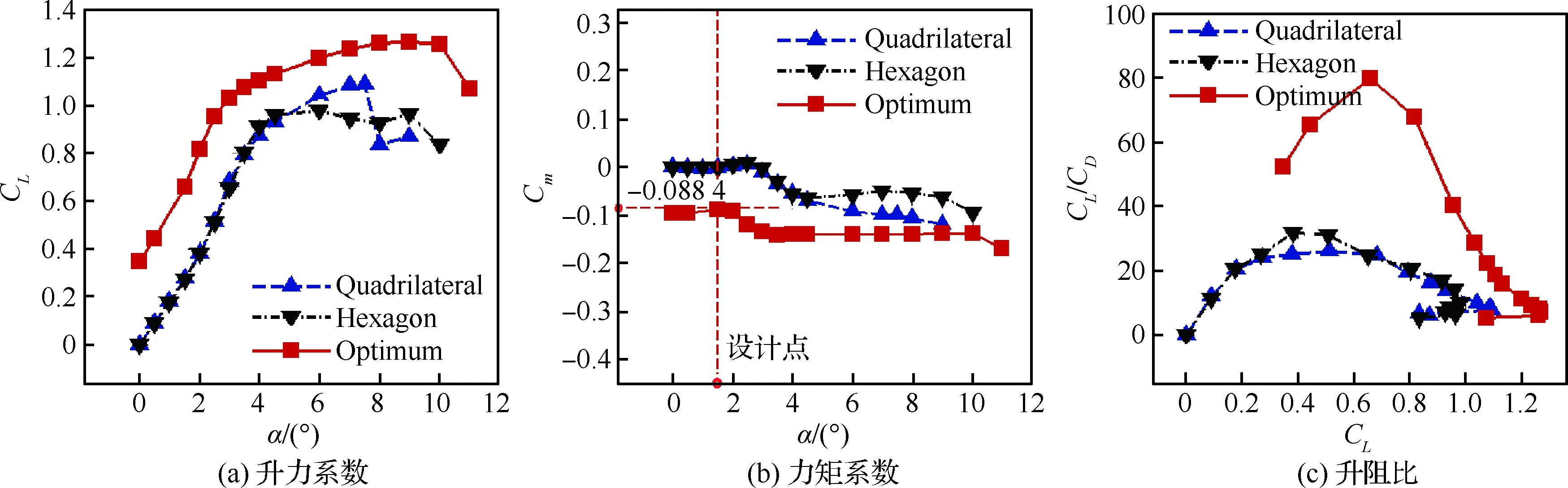
图16 跨声速状态下优化翼型与传统高超声速翼型的气动力特性对比(Ma=0.8, H=9 km, Re=7.6×106)Fig.16 Comparison of aerodynamic characteristics of optimized and conventional hypersonic airfoils in transonic flows (Ma=0.8, H=9 km, Re=7.6×106)

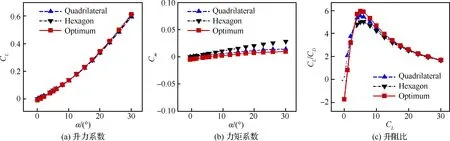
图17 高超声速状态下优化翼型与传统高超声速翼型的气动力特性对比(Ma=6, H=26 km, Re=4.23×106)Fig.17 Comparison of aerodynamic characteristics of optimized airfoil and conventional hypersonic airfoil in hypersonic flow (Ma=6, H=26 km, Re=4.23×106)

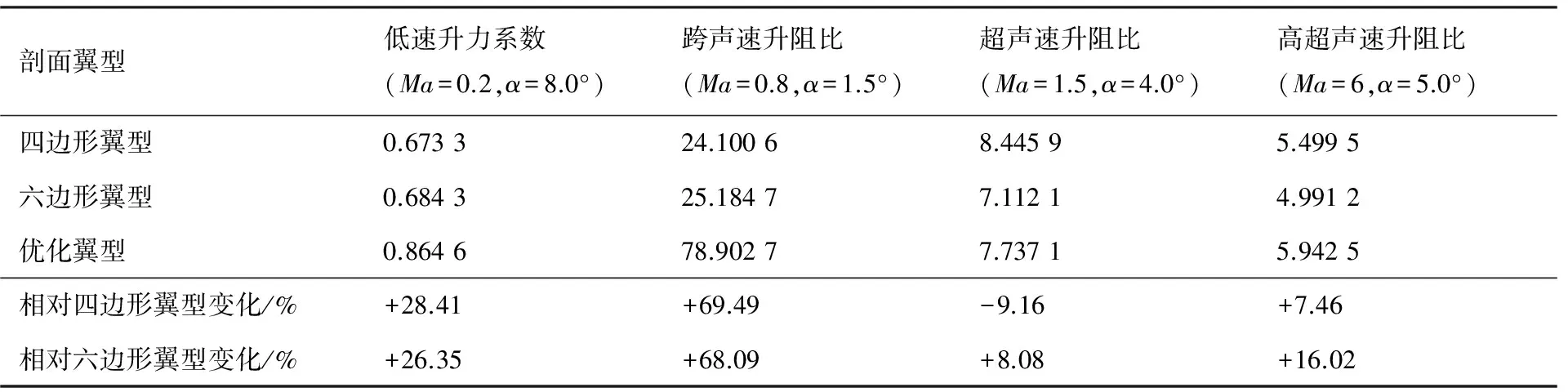
表3 不同马赫数下优化翼型与传统高超声速翼型气动特性对比Table 3 Comparison of aerodynamic characteristics of optimized and conventional hypersonic airfoils at different Mach numbers

由上述分析可知，本文设计的具有独特下表面双“S”型特征的翼型，能够很好地兼顾低速、跨声速、超声速和高超声速气动特性，有优良的宽速域气动性能。

4 宽速域机翼气动特性

为了综合分析配置了新翼型的机翼具有优良的宽速域气动特性，将配置了传统的四边形、六边形翼型的机翼与配置了宽速域翼型的机翼进行对比分析。传统高超声速翼型的外形参数如图11所示。机翼外形仿照德国“桑格尔号”空天飞机机翼，图18为 “桑格尔号”空天飞机外形设计图[16-17]。

机翼的平面外形参考“桑格尔号”空天飞机机翼，如图19所示。机翼计算网格采用结构化网格(图20)，网格量为300万。

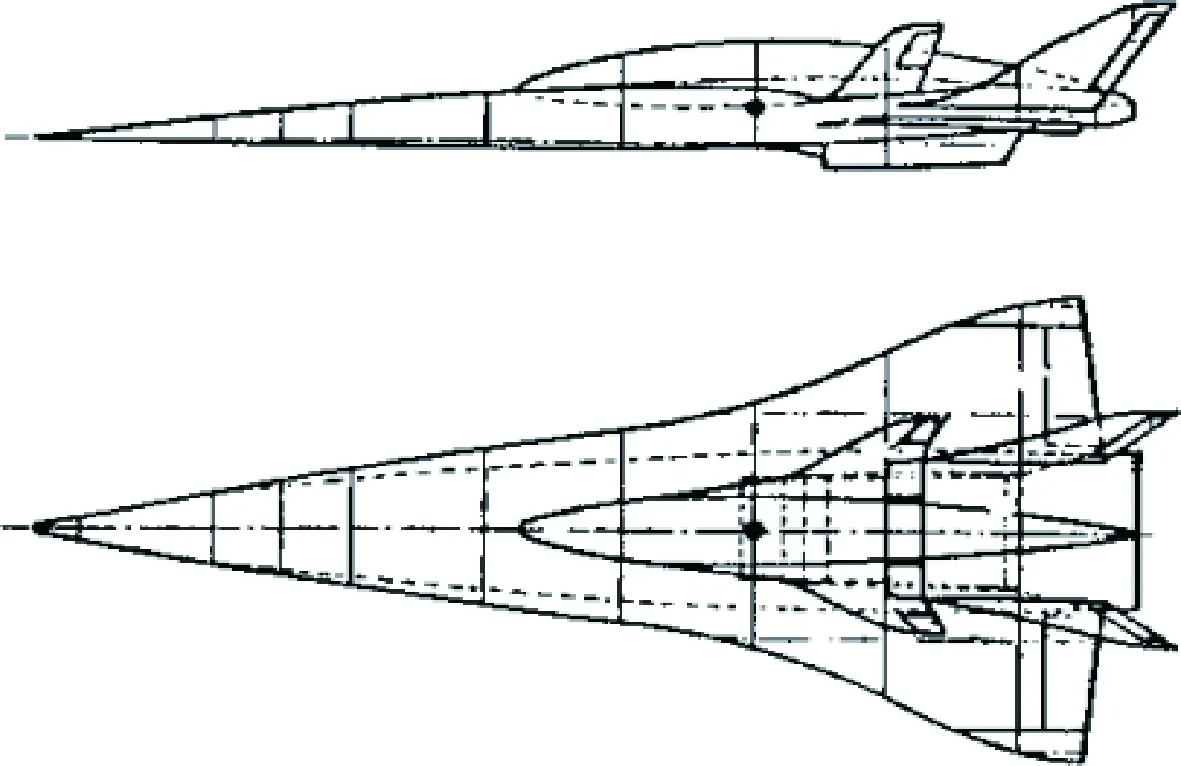
图18 “桑格尔号”空天飞机外形示意图[16-17]Fig.18 Schematic of “SANGER” airplane shape[16-17]

图19 仿“桑格尔号”空天飞机机翼平面外形示意图Fig.19 Schematic of a wing shape similar to “SANGER” airplane

图20 仿“桑格尔号”空天飞机机翼计算网格Fig.20 Computational grid for the wing similar to “SANGER” airplane

图21和图22为配置了不同翼型的机翼在跨声速和高超声速时上下表面压力云图的对比，其中p/pinf是当地压强和无穷远处来流压强的比值，V∞表示无穷远处来流速度。可以看出，配置了优化翼型的机翼在亚跨声速时下表面靠前缘处和靠后缘处都会产生明显的高压区，这一特性为其提供了额外的升力，保证了其优良的升力特性。超、高超声速状态下，机翼下表面靠后缘处会进行二次压缩，对升力特性进行补偿，保证了该翼型也能有较好的超、高超声速的升阻特性。可见，二维翼型的宽速域气动特性在三维机翼上同样能得到体现，并为其带来了气动上的优势。

图23和图24为配置了宽速域翼型(NPU-Hyper-04)与四边形、六边形翼型的机翼在宽速域状态下气动力系数的对比。表4为不同速域下，机翼在典型状态下的气动特性对比。可以明显看出，采用宽速域翼型的机翼在低速、跨声速时的升力系数和升阻比远远大于剖面形状为四边形、六边形翼型的机翼，相对提升量达到50%左右。在超声速状态下，其在小迎角下升力系数与升阻比也高于剖面形状为四边形、六边形翼型的机翼。在高超声速状态下，采用宽速域翼型的机翼在小迎角下气动特性与剖面翼型为四边形、六边形翼型的机翼的相当，但随着迎角的增大，其优势逐渐凸显出来。比较力矩系数曲线，在计算迎角范围内，俯仰力矩系数随迎角增加单调递减，故而飞行器是静稳定的。然而为了获得宽速域范围内优良的升阻特性，优化翼型损失了一些力矩特性，与剖面形状为四边形和六边形的机翼相比较，采用优化翼型的机翼力矩偏大。

图21 跨声速状态下剖面翼型为优化翼型与传统翼型的机翼表面压力云图对比(Ma=0.8, α=1.5°, Re=7.6×106)Fig.21 Comparison of surface pressure contours of wings with optimized airfoil and conventional airfoil in transonic flow (Ma=0.8, α=1.5°, Re=7.6×106)

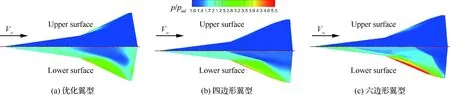
图22 高超声速状态下剖面翼型为优化翼型与传统翼型的机翼表面压力云图对比(Ma=6, α=5.0°, Re=4.23×106)Fig.22 Comparison of surface pressure contours of wings with optimized airfoil and conventional airfoil in hypersonic flow (Ma=6, α=5.0°, Re=4.23×106)

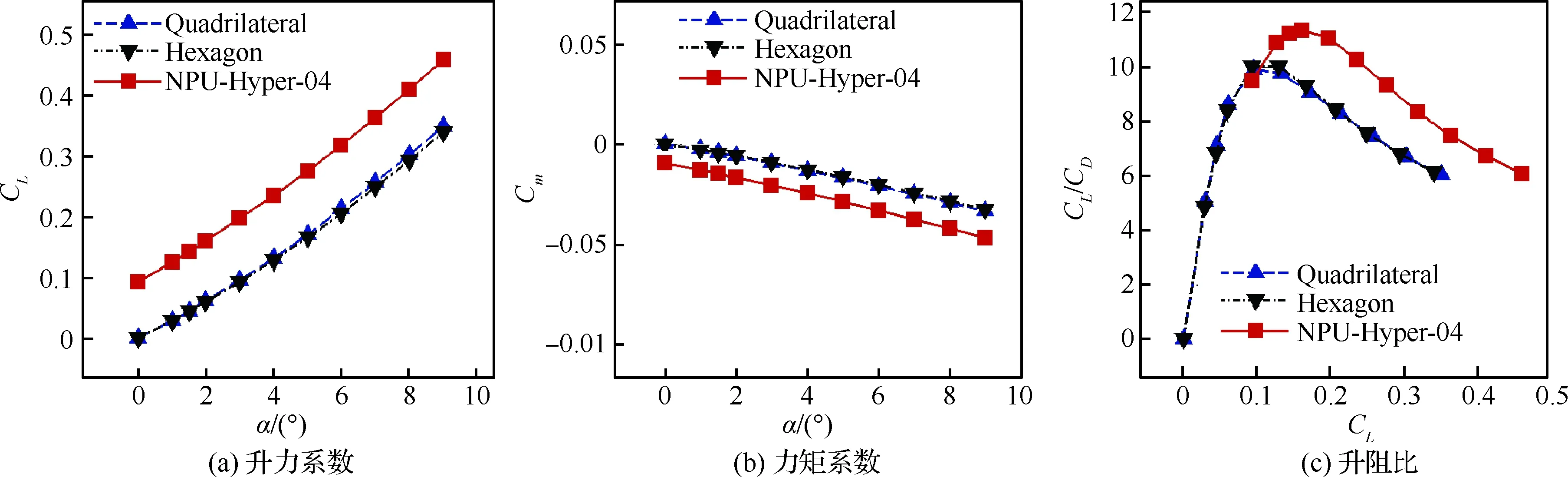
图23 跨声速状态下剖面翼型为优化翼型与传统翼型的机翼气动力系数对比(Ma=0.8, Re=7.6×106)Fig.23 Comparison of aerodynamic coefficient of wings with optimized airfoil and conventional airfoil in transonic flow (Ma=0.8, Re=7.6×106)

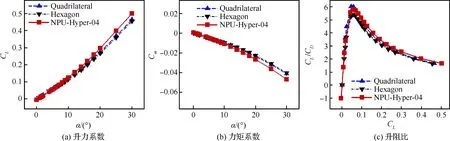
图24 高超声速状态下剖面翼型为优化翼型与传统翼型的机翼气动力系数对比(Ma=6, Re=4.23×106)Fig.24 Comparison of aerodynamic coefficient of wings with optimized airfoil and conventional hypersonic airfoil (Ma=6, Re=4.23×106)

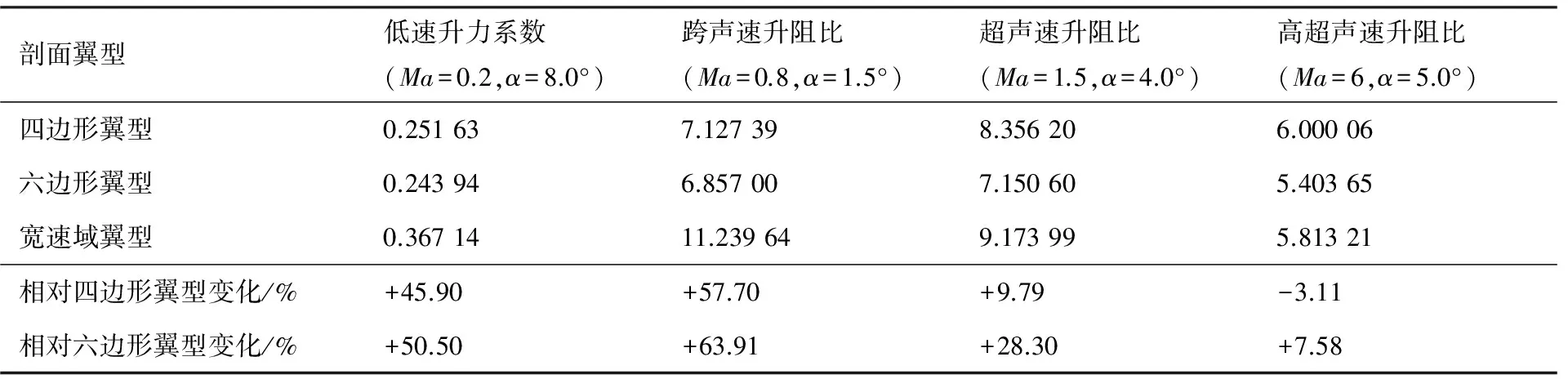
表4 不同马赫数下剖面翼型为优化翼型与传统高超声速翼型的机翼气动力系数对比Table 4 Comparison of aerodynamic coefficients of wings with optimized airfoil and conventional hypersonic airfoil at different Mach numbers

因此，配置了宽速域翼型的仿“桑格尔号”空天飞机机翼，在保证高超声速状态下的气动特性的同时，其亚、跨、超声速状态下的气动特性大幅度改善，具有优良的宽速域气动特性。可见，本文的宽速域翼型优化设计对于高超声速飞行器有一定的实用价值。

值得注意的是，本文以宽速域气动性能为目标的优化设计在三维构型中的优势还未能充分发掘。但对于这种小展弦比和大后掠机翼，机翼的三维效应非常显著。今后需要进一步在三维流动条件下开展宽速域机翼优化设计研究。

5 结 论

针对高超声速飞行器对宽速域气动特性的要求，采用最新发展的优化方法设计出了一种下表面具有双“S”特征的新翼型。将该翼型和常规高超声速翼型进行了综合气动对比，并将其配置到空天飞机机翼上，与配置常规高超声速翼型的机翼进行综合性能分析。

1) 与四边形、六边形翼型相比，下表面具有独特双“S”特征的新翼型的亚跨声速气动特性有大幅度提升，并且保证了超、高超声速气动特性，实现了宽速域范围内整体气动性能的显著提高。

2) 配置宽速域翼型的空天飞机机翼，与配置四边形和六边形等常规翼型的机翼气动性能相比，具有明显更优的宽速域特性。这证明了本文设计的翼型在三维机翼上同样具有一定的实用价值。

虽然所设计的翼型在三维机翼上取得了较好的效果，但由于机翼三维效应显著，今后需要基于所设计的新翼型直接在三维流动条件下对翼剖面进行优化，以获得更好的宽速域性能。