基于Busemann双翼的三维高超声速机翼研究

刘姝含，朱战霞,*

1. 西北工业大学 航天学院，西安 710072 2. 航天飞行动力学技术国家级重点实验室，西安 710072

自人类突破音障以来，人们一直在思考如何减小超声速飞行器的激波阻力，特别是飞行器进入高超声速飞行后，其激波阻力成为其总阻力的主要组成部分，减小激波阻力能够显著提高飞行器的气动效率，带来更高的经济价值。目前，如何减小超声速、高超声速飞行器的激波阻力已经得到世界各国研究人员的广泛关注[1]。

1935年，Busemann提出Busemann双翼用于减小超声速飞行的激波阻力[2]，通过使在Busemann双翼前缘产生的两道斜激波相交后，分别传播到翼型内部的喉道处，与此处产生的膨胀波进行干涉，从而减弱激波强度，以达到减小激波阻力的目的[3]。但由于Busemann双翼在非设计状态下容易产生流动壅塞现象，导致阻力迅速增大，因此Busemann双翼的研究一度陷入低谷。

近年来，Busemann双翼由于其在设计工作状态下显著的减阻能力而再次受到广泛关注。研究人员使用数值模拟方法[4]和风洞试验方法[5]研究Busemann双翼的气动特性，并利用Busemann双翼对飞行器的气动布局形式进行了研究[6-8]。Hu[9]和Yonezawa[10]等使用伴随方法对超声速双翼进行优化，解决了双翼在低马赫数下的部分流动壅塞问题；Licher[11]在对称的Busemann双翼基础上，提出了非对称的Licher双翼，提高了升阻比；日本Kusunose教授团队[12]使用反设计方法对Licher翼型进行优化；赵承熙等[13-14]使用反设计方法对Licher翼型进行优化并研究了超声速双翼的非定常流动问题，发现超声速双翼具有两种流动模式。Tian和Agarwal[15]使用遗传算法对Busemann双翼进行了优化，减小了Busemann双翼的阻力，提高了升阻比。

目前对Busemann双翼的研究多集中于Busemann双翼翼型在超声速流动中的优化问题[13-16]，而对Busemann双翼在高超声速流动中的气动特性[17]以及在三维机翼上的应用研究相对较少[18-20]。只有Kusunose团队[12]研究了超声速流动中三维Busemann机翼与机身的相对位置对三维Busemann机翼气动特性的影响;赵承熙等[20]研究了Busemann双翼在环翼上的应用。此类研究的对象均为超声速双翼，气动加热问题相对不明显，所以这些研究均未涉及机翼的结构特性。当Busemann双翼应用于高超声速机翼时，由于高超声速流动严重的气动加热效应，机翼温度显著升高，材料性能受到很大影响；同时，当Busemann双翼和菱形单翼具有相同的最大相对厚度时，Busemann双翼上下单翼的最大相对厚度仅为菱形单翼最大相对厚度的一半，双翼的结构性能将发生很大变化。因此有必要研究Busemann双翼在高超声速流动下的结构特性。

由于原有计算Busemann双翼升、阻力系数的理论公式仅适用于超声速流动，因此本文首先推导适用于高超声速流动状态下的Busemann双翼的升、阻力系数的理论计算公式，从理论上证明Busemann双翼在高超声速流动中能够提高升阻比；然后通过数值计算对高超声速Busemann双翼的气动特性和其提高升阻比、减小翼尖涡的机理进行研究；最后针对高超声速流动中复杂的热-流-固耦合问题，使用分层理论对高超声速机翼所涉及学科之间复杂的耦合关系进行简化，研究温度对高超声速机翼模态固有频率的影响，为Busemann双翼在高超声速飞行器上的实际应用提供参考。

1 Busemann双翼理论

1.1 增升效应

菱形单翼和Busemann双翼的示意图如图1和图2所示，菱形单翼4条边的压力系数分别用Cp1D～Cp4D表示，Busemann双翼6条边的压力系数分别用Cp1B～Cp6B表示，θ为菱形单翼前缘夹角的一半，也即Busemann双翼上、下单翼的前缘夹角,α为迎角。

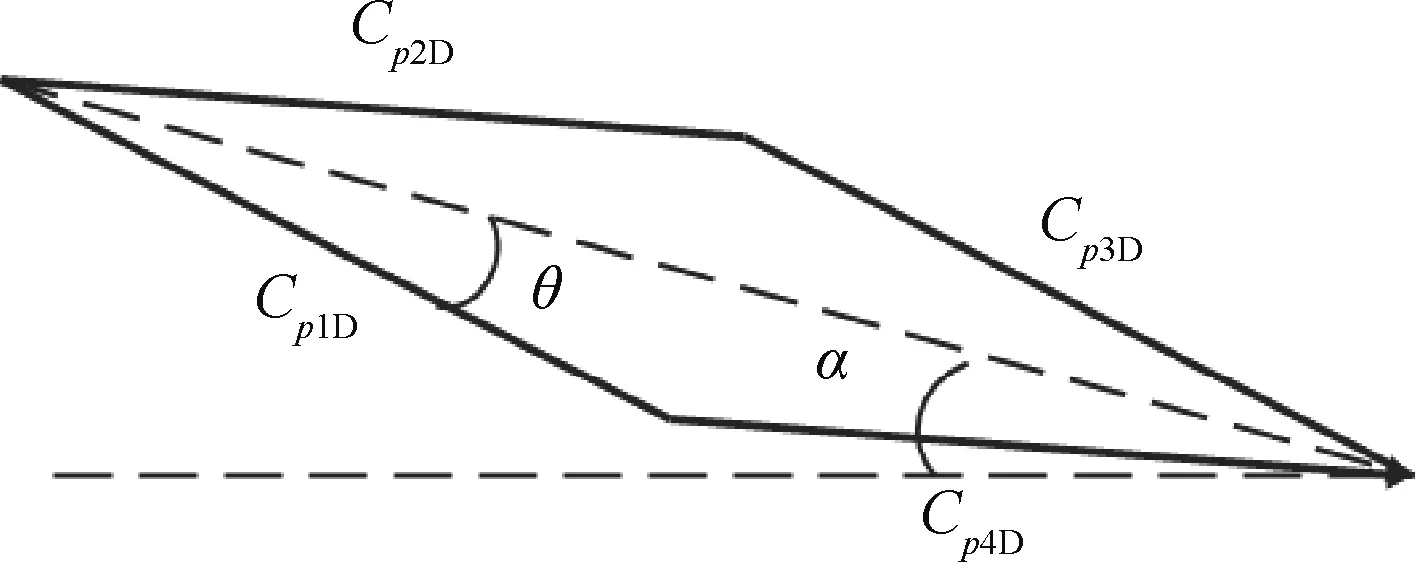
图1 菱形单翼Fig.1 Diamond airfoil

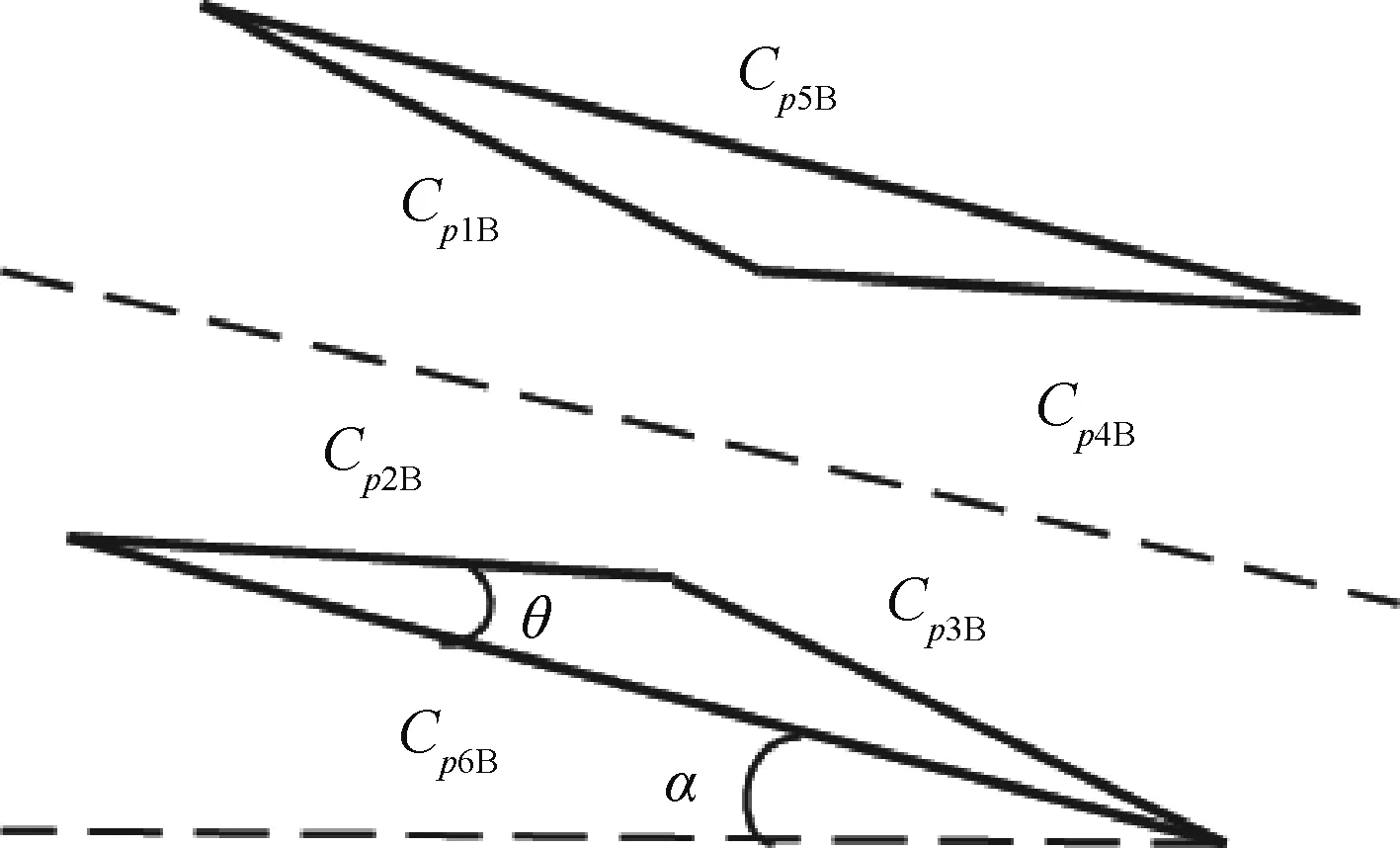
图2 Busemann双翼Fig.2 Busemann biplane

(1)

式中：p为迎风面观测点的压力；p∞为自由来流压力；q∞为自由来流动压；Ma∞为自由来流马赫数；β为激波角；γ为比热比。

(2)

式中：Man为斜激波后的马赫数；Δθ为气流经过观测点处的膨胀波时产生的气流偏转角。

由此对菱形单翼4条边的压力系数进行积分可以得到菱形单翼的升、阻力系数和升阻比分别为

(3)

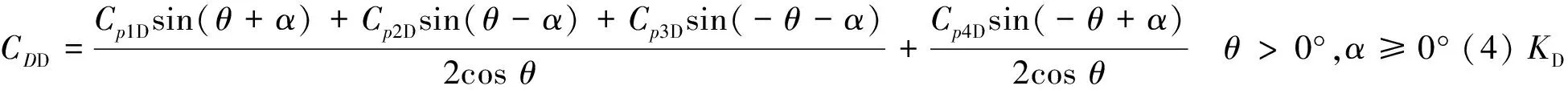
式中：CLD为菱形单翼的升力系数；CDD为菱形单翼的阻力系数；KD菱形单翼的升阻比。

同理，在不考虑激波与膨胀波干涉时可以得到Busemann双翼的升、阻力系数和升阻比为

CLB=CLD+-Cp5Bcos(-α)+Cp6Bcosα2cosθ

(6)

CDB=CDD+Cp5Bsin(-α)+Cp6Bsinα2cosθ

(7)

KB=CLBCDB

(8)

式中：CLB为Busemann双翼的升力系数；CDB为Busemann双翼的阻力系数；KB为Busemann双翼的升阻比。

由式(3)和式(4)可以得到

CLDCDD<-Cp5Bcos(-α)+Cp6BcosαCp5Bsin(-α)+Cp6Bsinα

(9)

当a>0，b>0，c>0，d>0且ab>cd时，有a+cb+d>cd,所以有

CLBCDB>CLDCDD

(10)

即

KB>KD

(11)

由此可见Busemann双翼的升阻比大于菱形单翼的升阻比。

1.2 激波膨胀波干涉减阻效应

菱形单翼和Busemann双翼的流场示意图如图3和图4所示,βD和βB分别为菱形单翼和Bosemann双翼的激波角。从图3和图4可以看出，Busemann双翼的气流经过了两道斜激波的压缩，而菱形单翼是经过一道斜激波的压缩，因此经过膨胀波膨胀后，气流在Busemann双翼后部产生的压力p2B将大于在菱形单翼后部产生的压力p2D,因此Busemann双翼后部将产生更大的向前的推力，所以Busemann双翼具有更小的阻力。

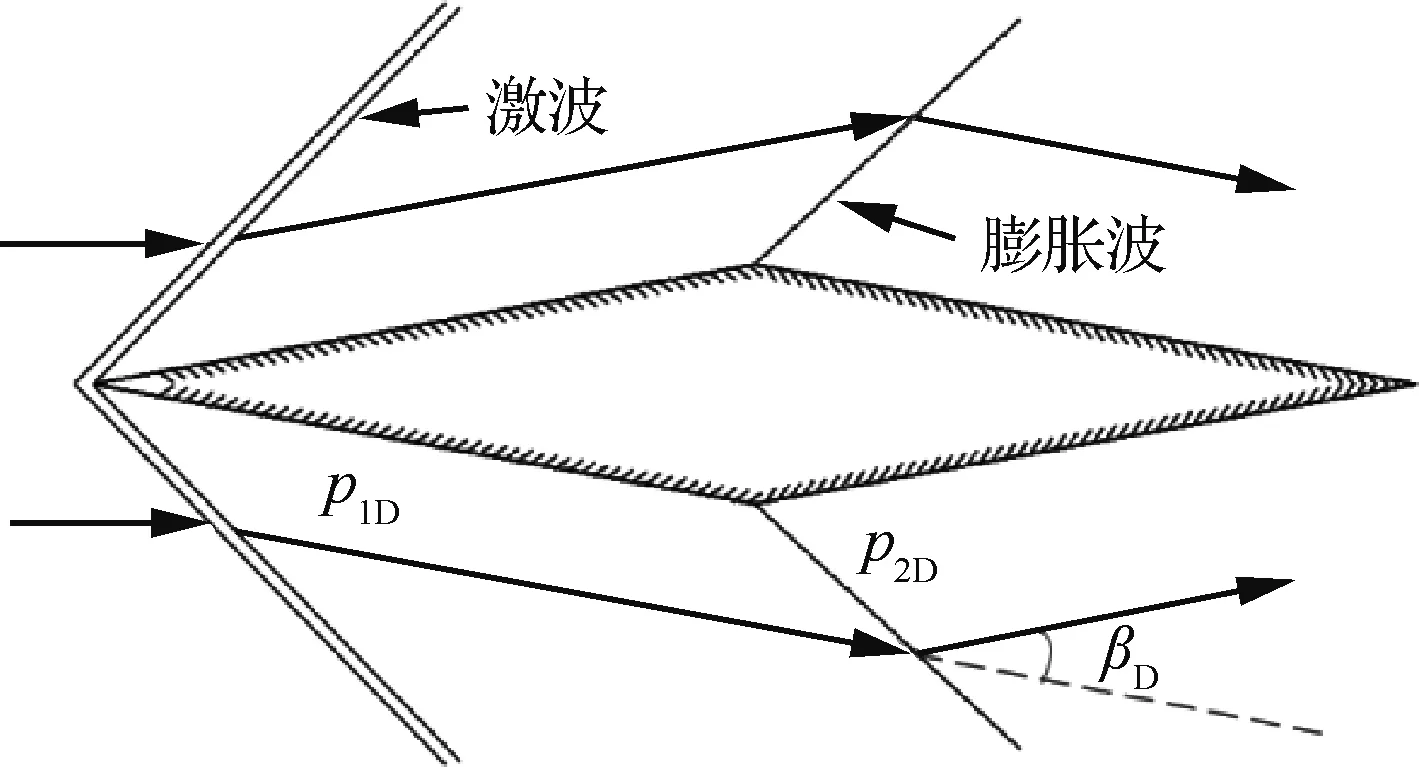
图3 菱形单翼流场Fig.3 Flowfield around diamond airfoil

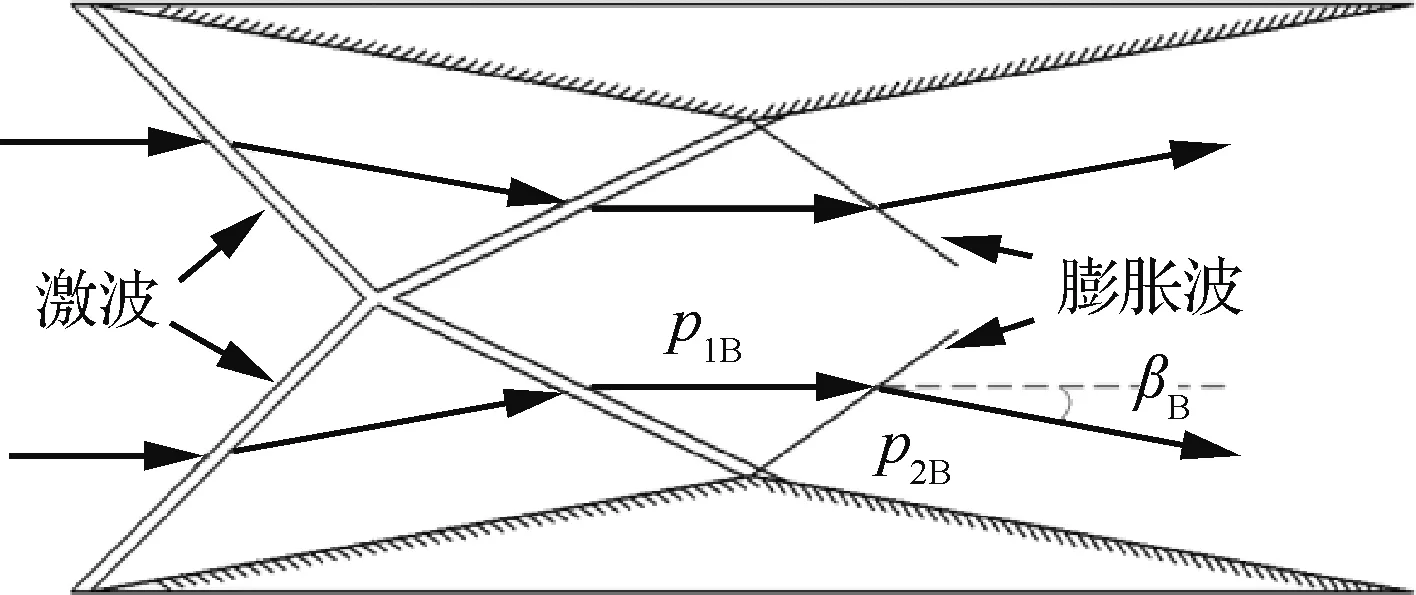
图4 Busemann双翼流场Fig.4 Flowfield around Busemann biplane

综合1.1节和1.2节可以得到，Busemann双翼翼型能够增加升力和减小阻力，从而提高气动性能。但研究其在高超声速机翼上的应用，还需要在考虑气动加热效应时进一步研究高超声速双翼的气动特性和结构性能。

2 高超声速静气动弹性计算

2.1 静热气动弹性问题的计算流程

高超声速飞行器的静热气动弹性问题涉及如何求解气动力/气动热、热传导和结构应力/应变等问题，整个过程包含：① 气动加热与结构温度之间的相互影响；② 气动力/气动热与结构变形之间的相互影响。数据计算流程如图5所示。

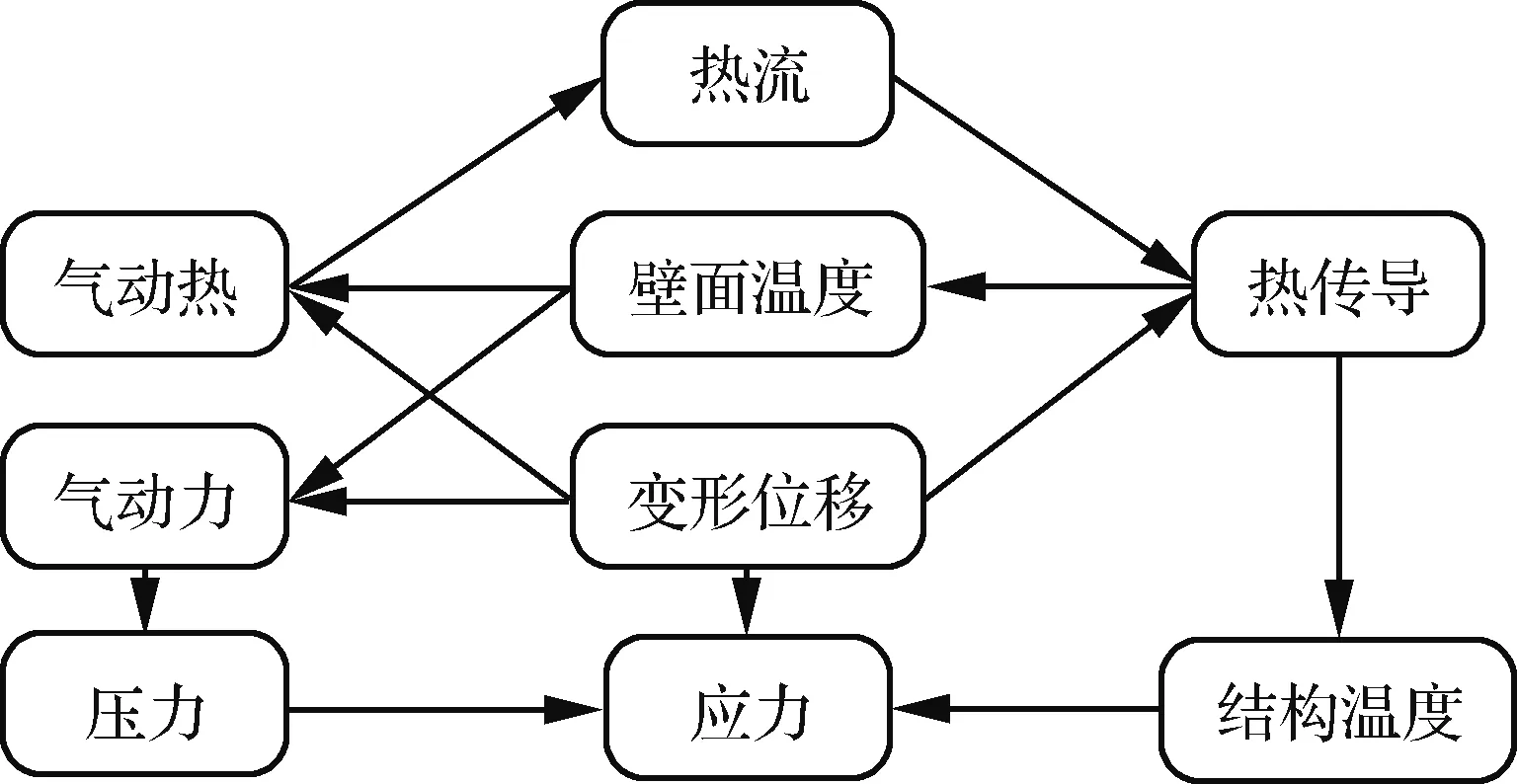
图5 静热气动弹性问题计算流程Fig.5 Calculation flowchart of static aerothermoelasticity problems

由于静态气动弹性问题主要研究飞行器结构的弹性变形对其升力和升力分布的改变，即高超声速飞行器静热气动弹性问题的关注点是结构的弹性变形和飞行器升力与升力分布的改变之间的影响关系。因此，可以做如下简化：

1) 忽略结构的变形速度，认为变形过程缓慢发生。

2) 使用定常求解方法求解计算气动力。

由此可知，在求解高超声速飞行器静热气动弹性问题时，可以不考虑沿时间的推进，而是直接使用结构平衡方程进行求解。

2.2 计算流程验证

中国科学院力学研究所对高超声速弹头进行了大量的试验研究，本文使用该所的弹头外形对静热气动弹性问题的计算方法和流程进行验证[21]。虽然弹头与机翼的外形有较大差别，但计算其热气动弹性的方法和流程是一致的，所以可以使用弹头模型对静热气动弹性问题的计算方法和流程进行验证。

计算模型如图6所示，计算条件为：自由来流马赫数为7.8，动压为0.87×105Pa；采用k-ε模型和基于密度基的求解方法，压力、动量和能量方程运用二阶迎风格式，时间项使用一阶隐式格式。

图6 弹头模型示意图Fig.6 Schematic diagram of a missile warhead model

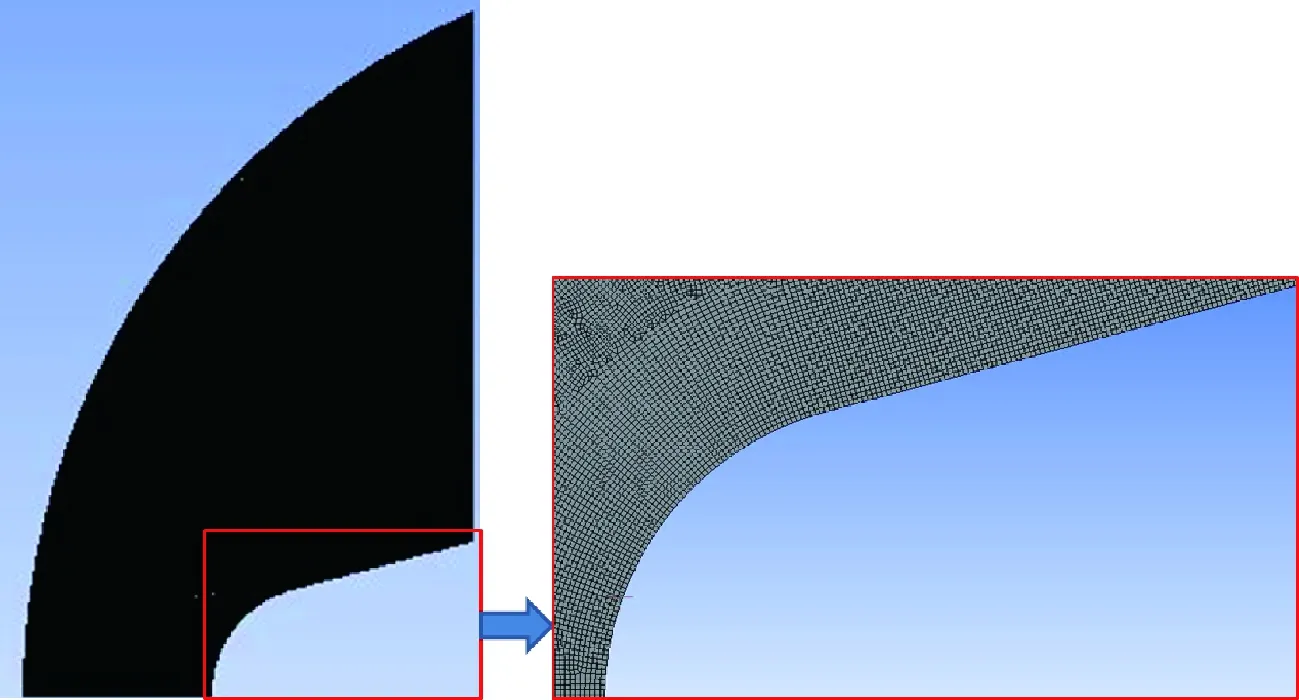
图7 弹头剖面的流场网格Fig.7 Flowfield mesh of section on a missile warhead model

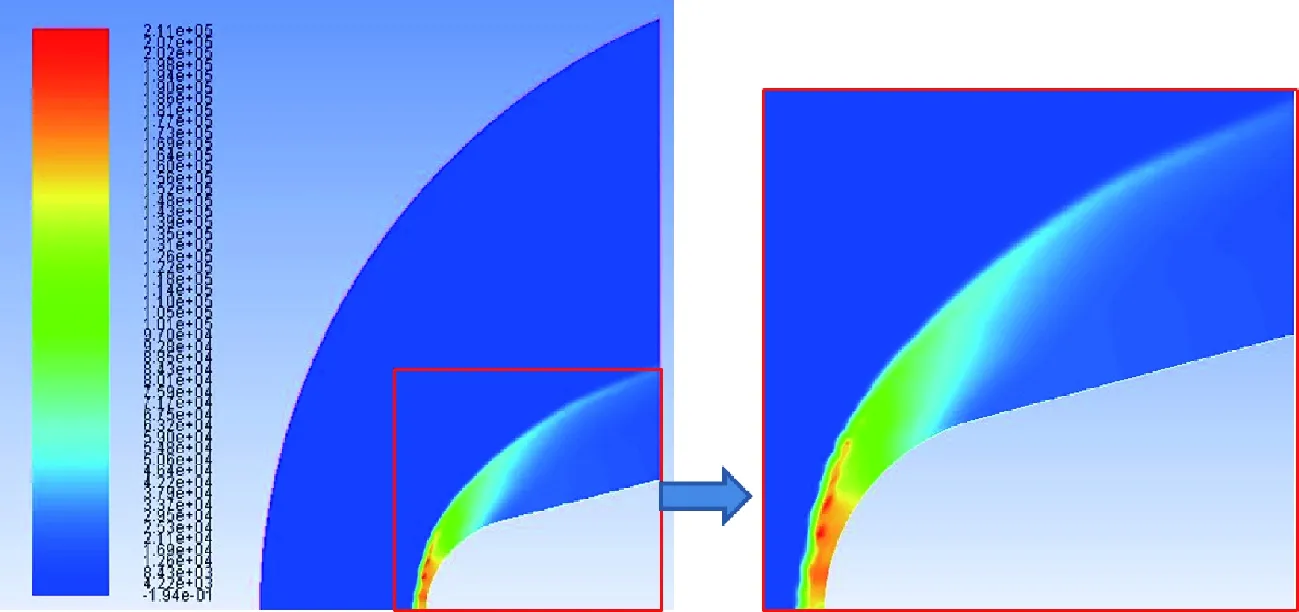
图8 弹头剖面的压力云图Fig.8 Pressure contour of section on a missile warhead model

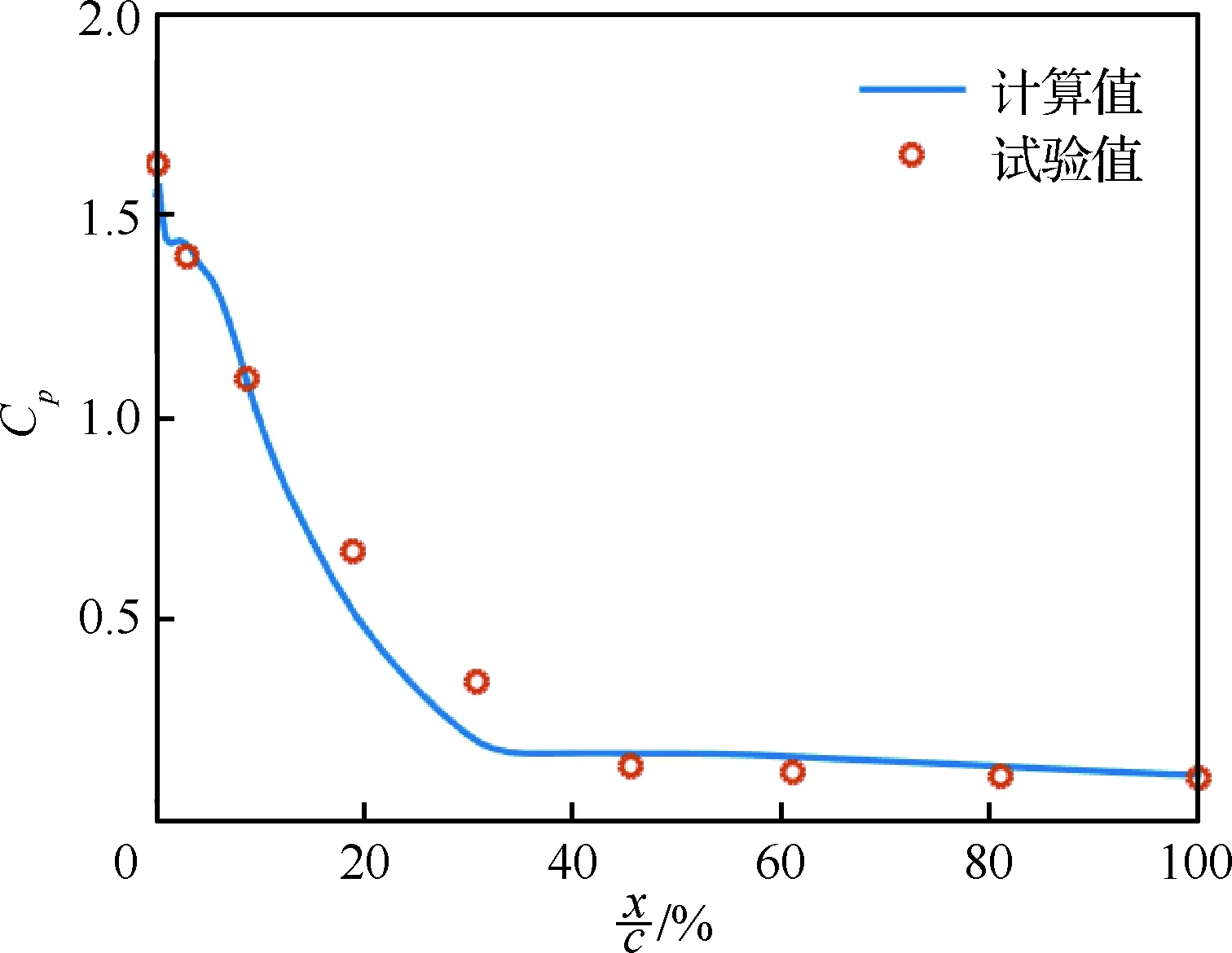
图9 弹头剖面压力系数对比Fig.9 Contrast of pressure coefficient of a missile warhead model

图7为弹头模型(如图6所示)剖面的流场网格图，网格质量最小为0.488，均值为0.983。图8为弹头模型剖面(如图7所示)的压力云图，图9为弹头模型剖面(如图7所示)表面压力系数Cp的CFD计算值和风洞试验值的对比。从图中可以看出，本文计算值和风洞试验值吻合较好，计算结果表明本文计算值与试验值的平均误差为1.5%，标准差为0.072，说明本文采用的耦合策略和数据分析计算流程是合理的，并且具有较高的计算精度。

3 Busemann双翼的气动特性

3.1 设计状态下的气动特性

3.1.1 机翼剖面的气动特性

由于Busemann双翼具有提高升阻比的特性，本文为提高高超声速飞行器三维机翼的升阻比，设计了一种使用Busemann双翼作为翼型的高超声速三维机翼，该机翼翼根弦长为2 m，梢根比为1，展长为0.8 m，双翼上、下单翼翼尖由一个翼尖隔板进行连接，其几何模型示意图如图10(a)所示。为分析Busemann双翼的气动特性，将其与常用的高超声速菱形单翼的气动特性进行横向对比。因此设计菱形单翼的翼根弦长为2 m，梢根比为0.3，展长为1.3 m，几何模型示意图如图10(b)所示。其中，Busemann双翼翼型和菱形单翼翼型的几何夹角θ和迎角α均取为3°。

分别在Busemann双翼和菱形单翼展长的0，25%，50%，75%，100%处设置观察站位，其示意图如图11所示。

设置菱形单翼的流场长度为菱形单翼平均气动弦长的30倍，流场宽度为菱形单翼展长的4倍，流场高度为菱形单翼平均气动弦最大厚度的20倍。对流场进行非结构网格划分，得到607万网格，网格质量最小值为0.176，最大值为0.999，平均值为0.92。局部网格如图12(a)所示。设置Busemann双翼的流场长度为双翼弦长的30倍，流场宽度为双翼展长的4倍，流场高度为双翼厚度的20倍。对流场进行非结构网格划分，得到632万网格，网格质量最小值为0.165，最大值为0.999，平均值为0.90。局部网格如图12(b)所示。

图10 机翼几何模型Fig.10 Geometry model of wings

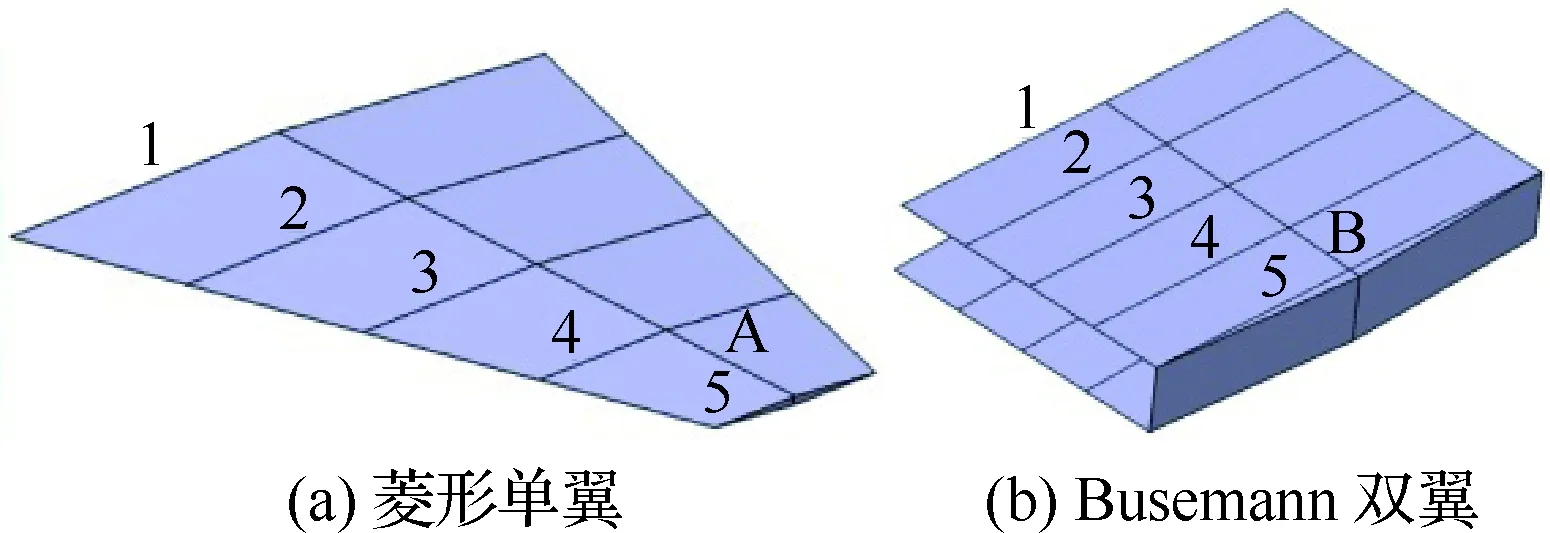
图11 压力系数观测站位Fig.11 Pressure coefficient observation station

将Busemann双翼和菱形单翼的飞行高度设置为30 km，来流马赫数为5，机翼表面为壁面，计算域表面为压力远场。采用k-ε模型和基于密度基的求解方法，压力、动量和能量方程运用二阶迎风格式，时间项的处理使用一阶隐式格式。图13为双翼和单翼分别在3站位处的流场压力分布图。

图12 机翼流场局部网格Fig.12 Local mesh of flow field around wings

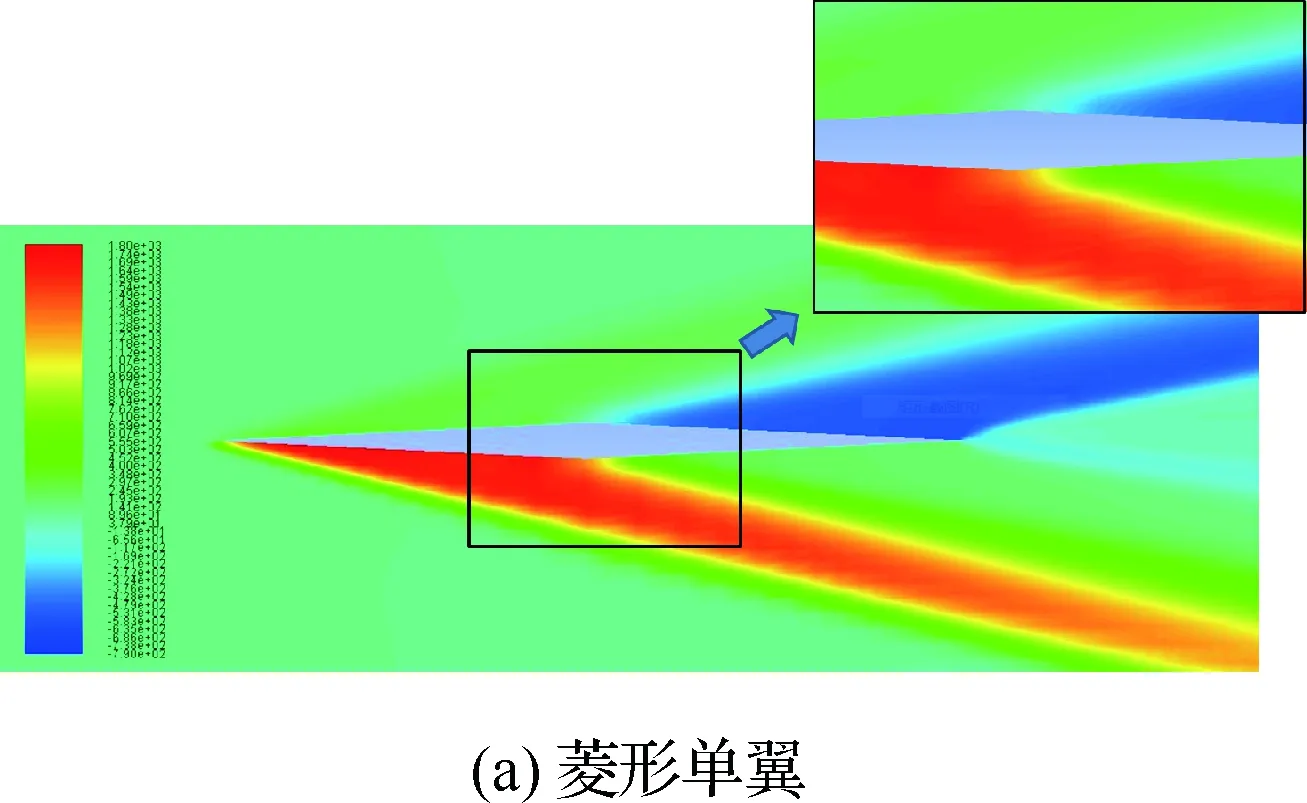
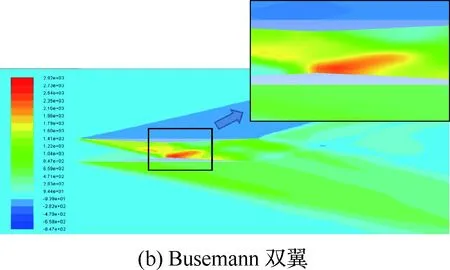
图13 机翼剖面的压力分布Fig.13 Pressure distribution of wings’ section

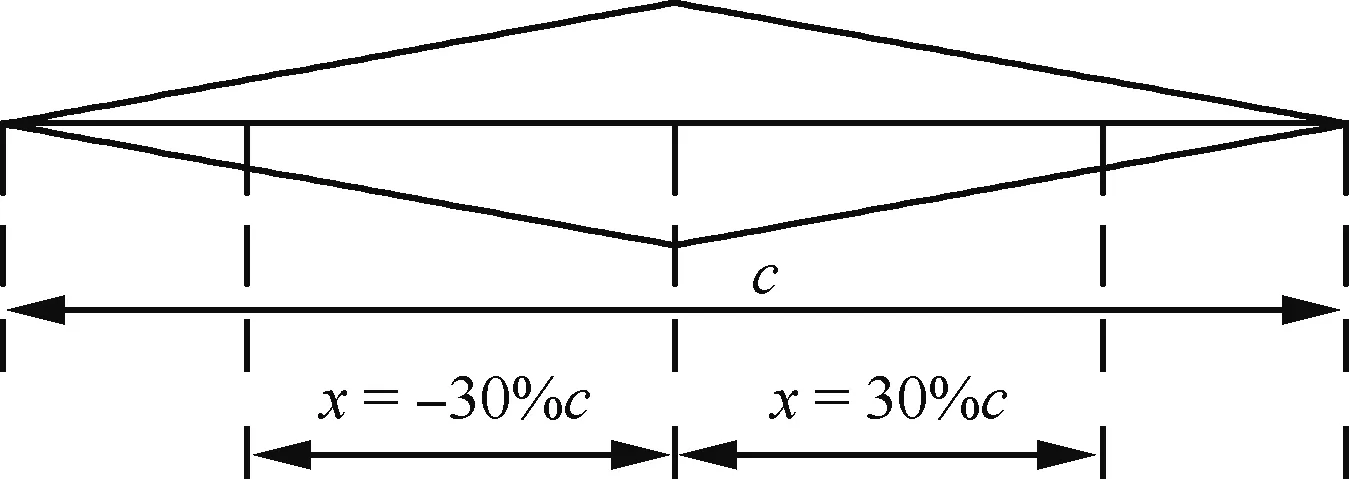
图14 横坐标x的物理意义Fig.14 Physical meaning of abscissa x

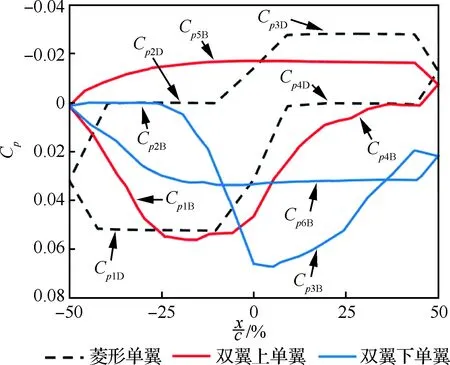
图15 机翼表面压力系数Fig.15 Surface pressure coefficient of wings

以观察站位上的压力测试点在相应的翼剖面弦线上的站位作为横坐标(如图14所示，c为机翼弦长)，相应的压力系数作为纵坐标，构建机翼的压力系数曲线如图15所示。图15是菱形单翼在3站位处和Busemann双翼上、下单翼在3站位处的表面压力系数的CFD计算值对比。

从图15中可以看出，在靠近前缘部分，双翼的Cp1B小于菱形单翼的Cp1D,在靠近50%弦长时，双翼的Cp1B大于菱形单翼的Cp1D;在Busemann双翼的前缘部分，由于激波与膨胀波的相互干涉，所以上单翼前缘部分的压强减小。在靠近50%弦长时，上单翼产生的斜激波打在下单翼后发生反射，反射气流再次打在上单翼的后部，所以双翼的Cp4B大于菱形单翼的Cp4D,而增大Cp4B有利于双翼减小阻力和增大升力。

从图15中还可以发现双翼的Cp3B远大于菱形单翼的Cp3D,图13(b)表明双翼上单翼产生的斜激波打在下单翼后与下单翼喉部产生的膨胀波发生干涉，导致Cp3B增大，虽然增大Cp3B对双翼的升力产生了不利影响但有利于减小双翼的阻力。

对比图13(a)和图13(b)可见，相对于菱形单翼，激波与膨胀波的相互干涉使Busemann双翼的激波强度显著减弱，并使双翼上、下单翼后部的压力增大，从而产生推力，减小了双翼的阻力。

表1为CFD计算得到的Busemann双翼和菱形单翼的气动特性。

表1 Busemann双翼和菱形单翼的气动特性Table 1 Aerodynamic characteristics of Busemann biplane and diamond airfoil

注：CL为升力系数，CD为阻力系数，K为升阻比。

分析表1中菱形单翼和Busemann双翼的升、阻力系数可以发现，相对于菱形单翼的升、阻力系数，双翼的升力系数提高了28.95%，阻力系数增大了13.58%，升阻比增加了13.53%，可见在高超声速流动中，Busemann机翼能够显著地提高升阻比。表1表明在考虑黏性后，由于双翼的表面积较大，摩擦阻力更大，所以增加的摩擦阻力抵消了激波膨胀波干涉效应减小的激波阻力，因此双翼的总阻力更大，阻力系数更大。但随着马赫数的增大，激波阻力在总阻力中的占比增大，在马赫数达到一个临界值后，摩擦阻力的增大量将小于激波阻力的减小量，此时Busemann的气动性能将进一步提高。

3.1.2 机翼沿展向的气动特性

以5个观察站位上的压力测试点在相应的翼剖面弦线上的站位作为横坐标，相应的压力系数作为纵坐标，构建机翼沿展向5个站位的压力系数曲线，如图16所示。

图17为菱形单翼A截面(如图11(a)所示)的压力分布，图18为Busemann双翼B截面(如图11(b)所示)的压力分布。

图16(a)表明，菱形单翼在沿展向的观察站位1～4上，对应压力测试点的压力系数均相差不大，但在观察站位5上，对应压力测试点的压力系数绝对值显著减小。图17表明在菱形单翼的翼尖部分，由于机翼上、下表面较大的压力差，使得机翼下表面的空气绕过翼尖流向上表面，导致上、下表面的空气得以沟通，从而使得上、下表面的压力系数显著减小。同时，图16(a)和图17也表明这一现象仅发生在翼尖部分。

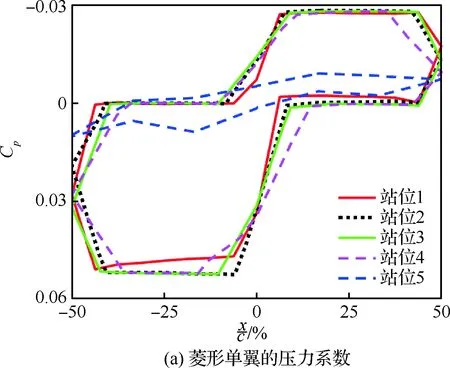
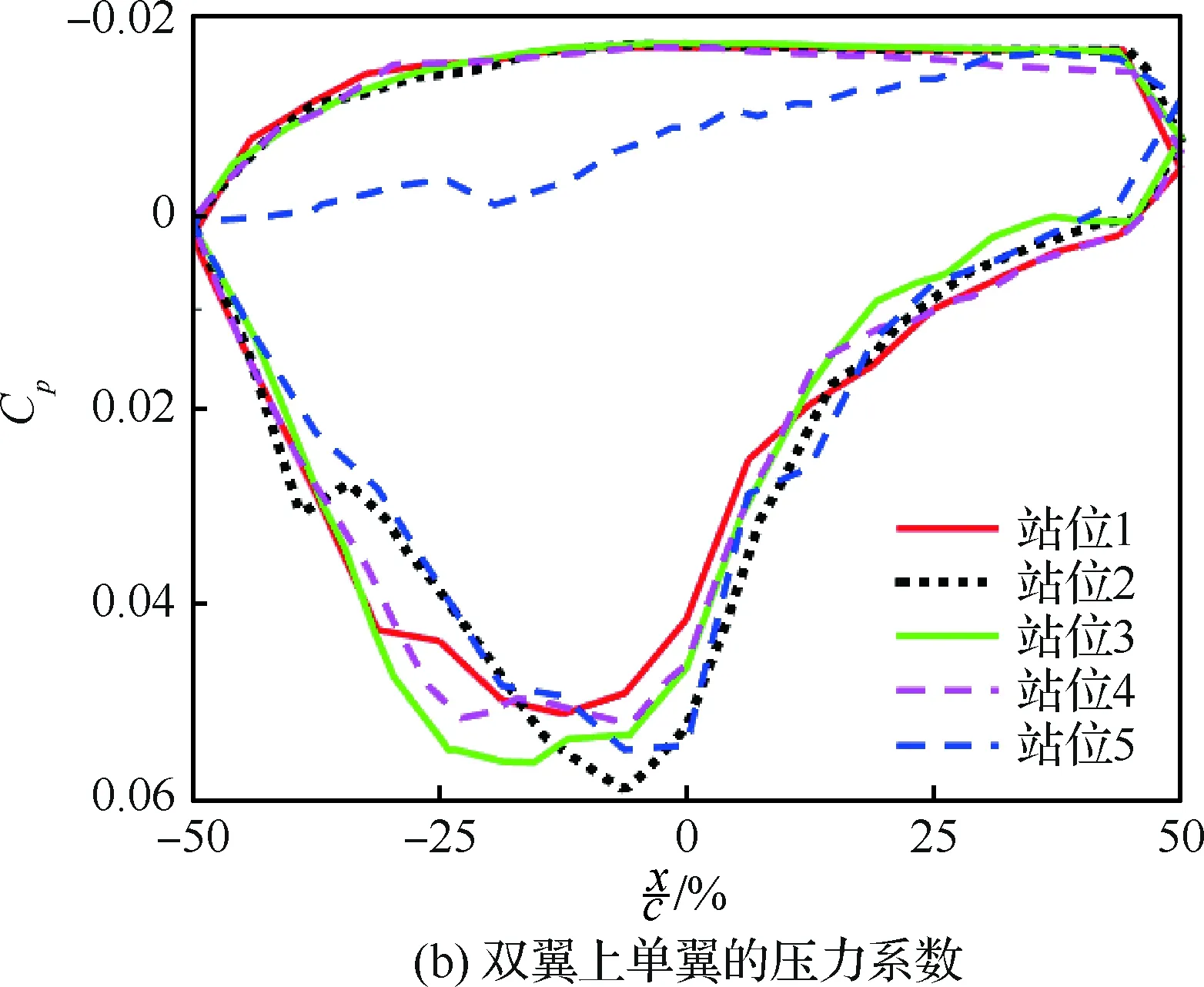
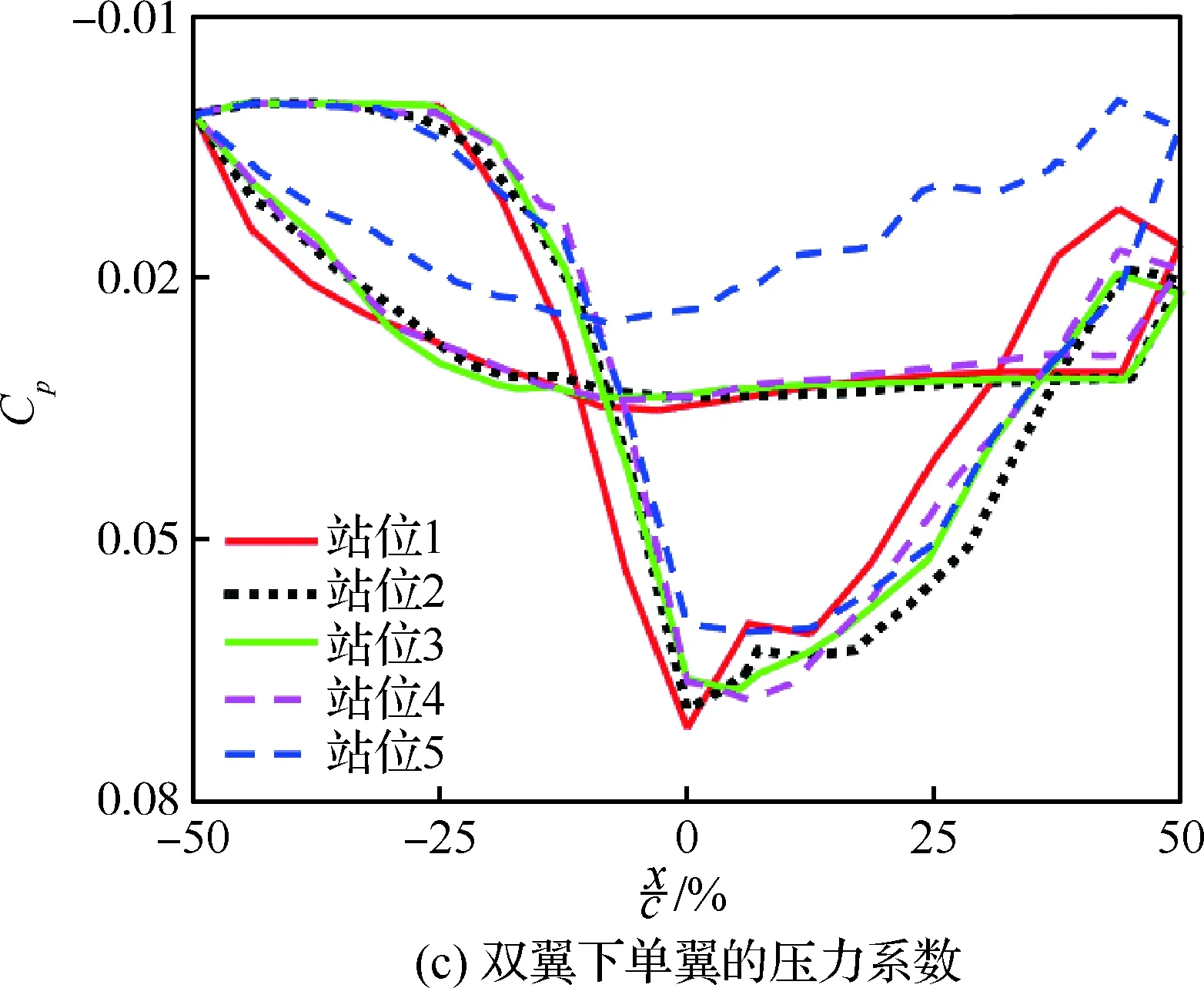
图16 机翼站位压力系数Fig.16 Pressure coefficient of wing station

图17 菱形单翼A截面的压力分布Fig.17 Pressure distribution of Section A of diamond wing

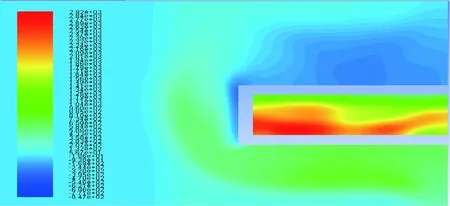
图18 Busemann双翼B截面的压力分布Fig.18 Pressure distribution of Section B of Busemann biplane

结合图16(b)、图16(c)和图18可以发现，Busemann双翼由于翼尖端板的隔离，Busemann双翼内流道的空气无法与双翼外的空气进行沟通，双翼上单翼的下表面和下单翼的上表面在观察站位1～5上的压力系数基本保持不变。结合图11(b)、图16(b)、图16(c)和图18可以发现，由于翼尖端板在前缘产生高压，在后缘产生低压，上、下单翼在翼尖区域的气流发生沟通，使得在观察站位5上,上单翼前缘上表面的压力系数增大，下单翼后缘下表面的压力系数减小。

从图16～图18可见，Busemann双翼翼尖处上、下表面压力系数的变化小于菱形单翼翼尖处上、下表面压力系数的变化。分析其原因有：① Busemann双翼由于翼尖端板的隔离，使得双翼内流道的气流不能与外部气流进行相互流动；② 双翼上单翼上表面与下单翼下表面的间距比菱形单翼上下表面间距大，减缓了上下表面间的空气流动，因此压力系数变化较小，翼尖涡强度较弱。

3.2 非设计状态下的气动特性

Busemann双翼在非设计状态下的气动特性迅速变差主要是指Busemann双翼在非设计马赫数和非设计迎角下进行飞行时，Busemann双翼的气动特性快速变差。因此，本文分别对Busemann双翼和菱形单翼在状态1和状态2时的气动特性进行研究。状态1和状态2的定义如下：

状态1马赫数为1，迎角为3°。

状态2马赫数为5，迎角为8°。

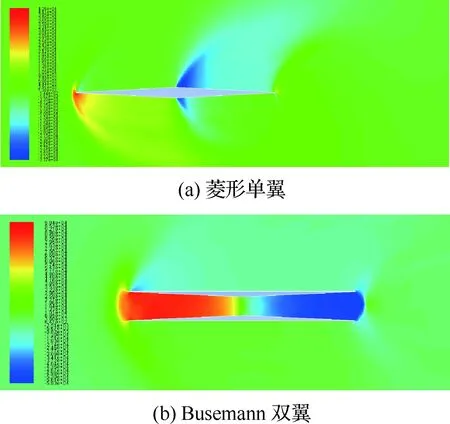
图19 机翼在站位3处的压力分布(Ma=1,α=3°)Fig.19 Pressure distribution of Station 3 of wings(Ma=1,α=3°)

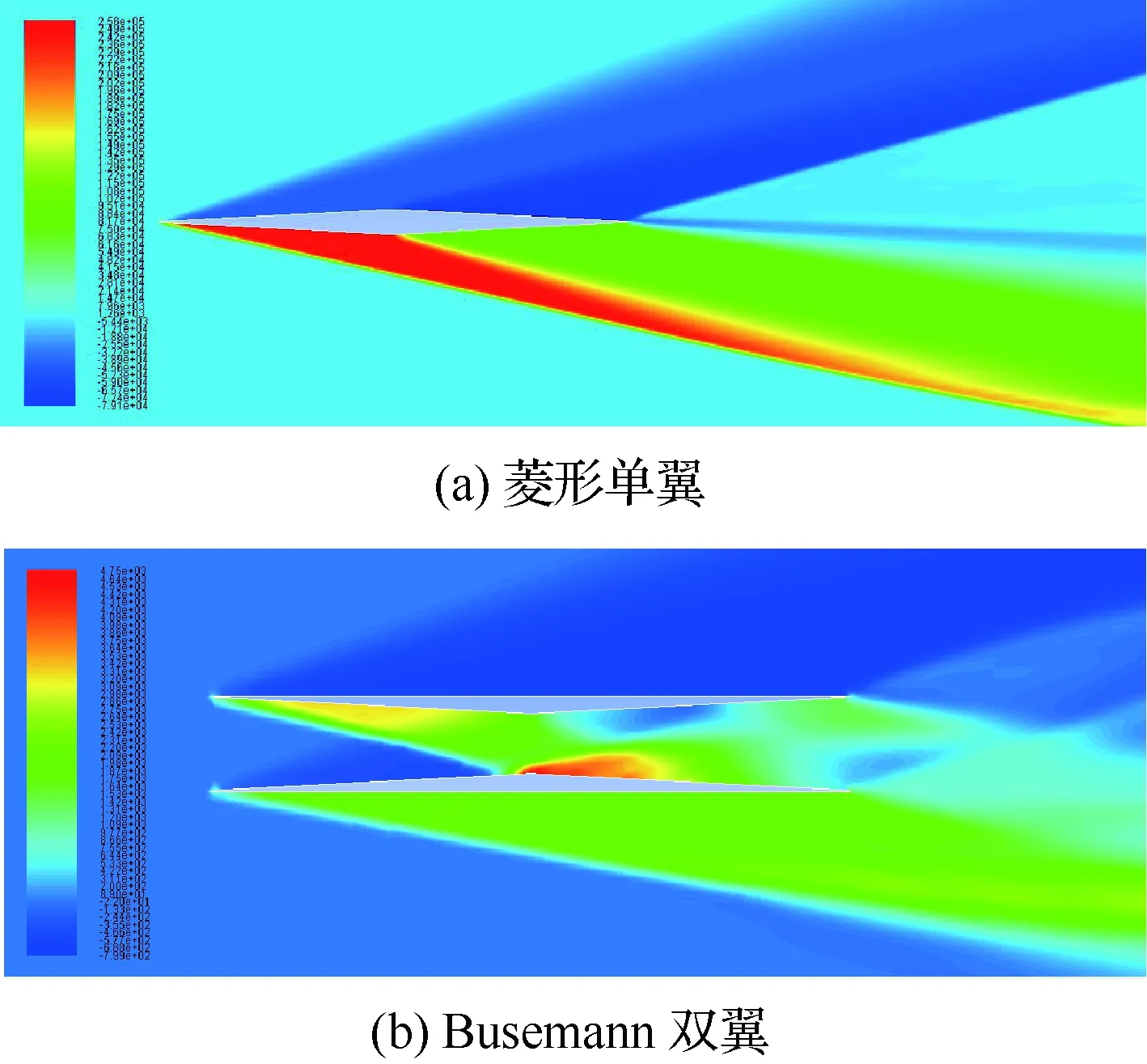
图20 机翼在站位3处的压力分布(Ma=5,α=8°)Fig.20 Pressure distribution of Station 3 of wings(Ma=5,α=8°)

流场网格采用如图12所示的网格，计算得到菱形单翼和Busemann双翼在跨声速和大迎角飞行时的气动特性，分别如图19和图20所示。图19表明在马赫数为1、迎角为3°时，Busemann双翼的前部产生了明显的流动壅塞现象；图20表明在马赫数为5、迎角为8°时，Busemann双翼上单翼前缘产生的激波和下单翼前缘产生的膨胀波在喉道前部产生了明显干涉现象，且并未出现流动壅塞现象。

表2为菱形单翼和Busemann双翼分别在状态1和状态2时的升、阻力系数和升阻比。从表中可以看出，在状态1条件下，由于出现了流动壅塞现象，相比于设计状态，菱形单翼的升阻比下降了15.2%，Busemann双翼的升阻比显著下降了54.3%；在状态2条件下，相比于设计状态，菱形单翼的升阻比下降了7.5%，Busemann双翼的升阻比下降了12.3%。通过对菱形单翼和Busemann双翼在非设计状态下的气动特性进行分析，可以发现Busemann双翼在非设计状态下飞行时，其升阻比均有明显下降，所以在实际应用时应关注双翼在非设计状态下的气动性能。

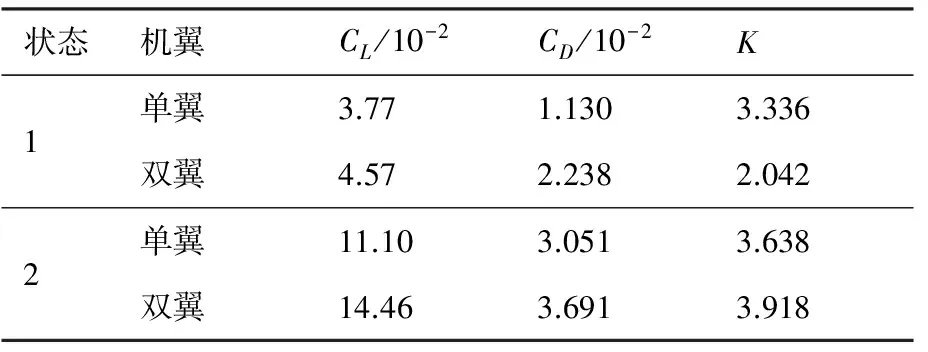
表2 不同状态下的气动特性Table 2 Aerodynamic characteristics of different states

4 Busemann双翼的模态分析

Busemann双翼虽然能够在设计状态下明显提高升阻比，但要将其应用于实际飞行中的高超声速机翼，还需要考虑其他因素的影响。

当Busemann双翼和菱形单翼具有相同的相对厚度时，Busemann双翼上下单翼的相对厚度仅为菱形单翼相对厚度的一半，因此Busemann双翼结构性能可能降低，从而较早地达到临界颤振速度，导致产生安全问题。本文将研究温度对Busemann双翼和菱形单翼前6阶模态的影响。

由于飞行器巡航过程中升力与重力相等，因此基于Busemann双翼和菱形单翼产生的升力相等的原则，设计菱形单翼尺寸为：翼根弦长为2 m，梢根比为0.3，展长为1.3 m；Busemann双翼尺寸为：翼根弦长为2 m，梢根比为1，展长为0.655 m。其中，Busemann双翼翼型和菱形单翼翼型的几何夹角θ和迎角α均取为3°。Busemann双翼和菱形单翼均选择高温合金材料GH1015[22]作为机翼的结构材料。

本文采用分层理论进行求解，将气动力-气动热-结构的多物理场耦合分解为气动热-结构耦合和气动力-结构耦合两部分分别进行求解[22]，忽略结构变形对热环境的影响，同时由于采用小展弦比(展弦比不大于1)机翼，机翼变形不大，所以忽略结构变形对气动力的影响，因此将耦合过程简化为单向耦合。具体求解过程为：① 采用CFD方法计算气动力和气动热；② 将热载荷加载到结构上，得到结构的温度场；③ 在相应温度场下求解结构的热应力；④ 将热应力作为预应力，气动力作为载荷加载到结构上进行模态分析，得到结构的振型和固有频率。

设置仿真环境：飞行高度为30 km，迎角为3°，马赫数为5。经计算后得到菱形单翼和Busemann双翼的前6阶模态振型如图21和图22所示。

在图21(a)和图22(a)中，菱形单翼和Busemann双翼的法向位移最大值均出现在翼尖位置；在图21(b)中，菱形单翼的最大扭转位置出现在机翼翼尖的后缘，在图22(b)中， Busemann双翼的最大扭转位置出现在机翼中部的前后缘。因此在设计中需要增加菱形单翼翼尖后缘和Busemann机翼中部前后缘的刚度，以提高其结构性能，保证飞行安全。

经过CFD计算得到菱形单翼和Busemann双翼的温度分布云图，如图23所示。图24为菱形单翼和Busemann双翼的表面温度T的分布曲线，从图中可以看出两者的表面温度均在1 300 ℃左右。

图25为菱形单翼前6阶模态的固有频率f随温度的变化关系；图26为Busemann双翼前6阶模态的固有频率随温度的变化关系。

从图25和图26可见，Busemann双翼和菱形单翼前6阶模态的固有频率均随着温度的升高而减小，Busemann双翼4～6阶模态的固有频率均分别小于菱形单翼4～6阶模态的固有频率，2阶和3阶模态的固有频率分别基本相当，而1阶模态的固有频率稍大于菱形单翼1阶模态的固有频率。在前6阶模态中，1阶模态(1阶弯曲模态)的固有频率均明显小于各自的其他阶模态的固有频率，因此，应重点关注机翼的弯曲特性。

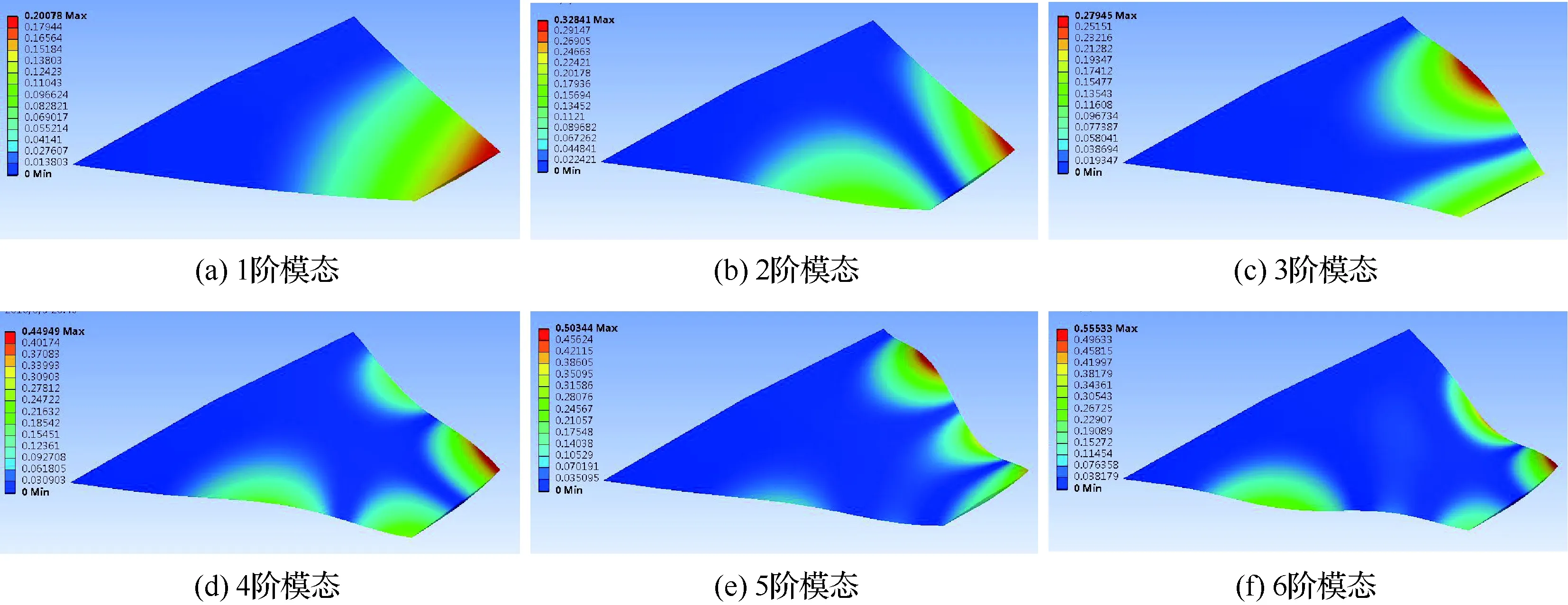
图21 菱形单翼前6阶模态振型Fig.21 Vibration type of first six modes of diamond airfoil

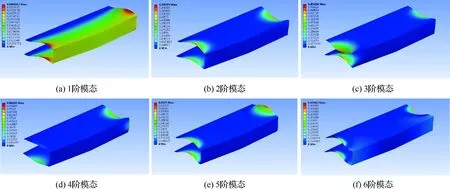
图22 Busemann双翼前6阶模态振型Fig.22 Vibration type of first six modes of Busemann biplane

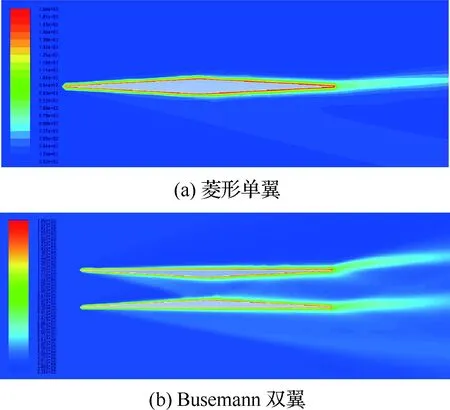
图23 流场剖面温度Fig.23 Temperature of section of flowfield

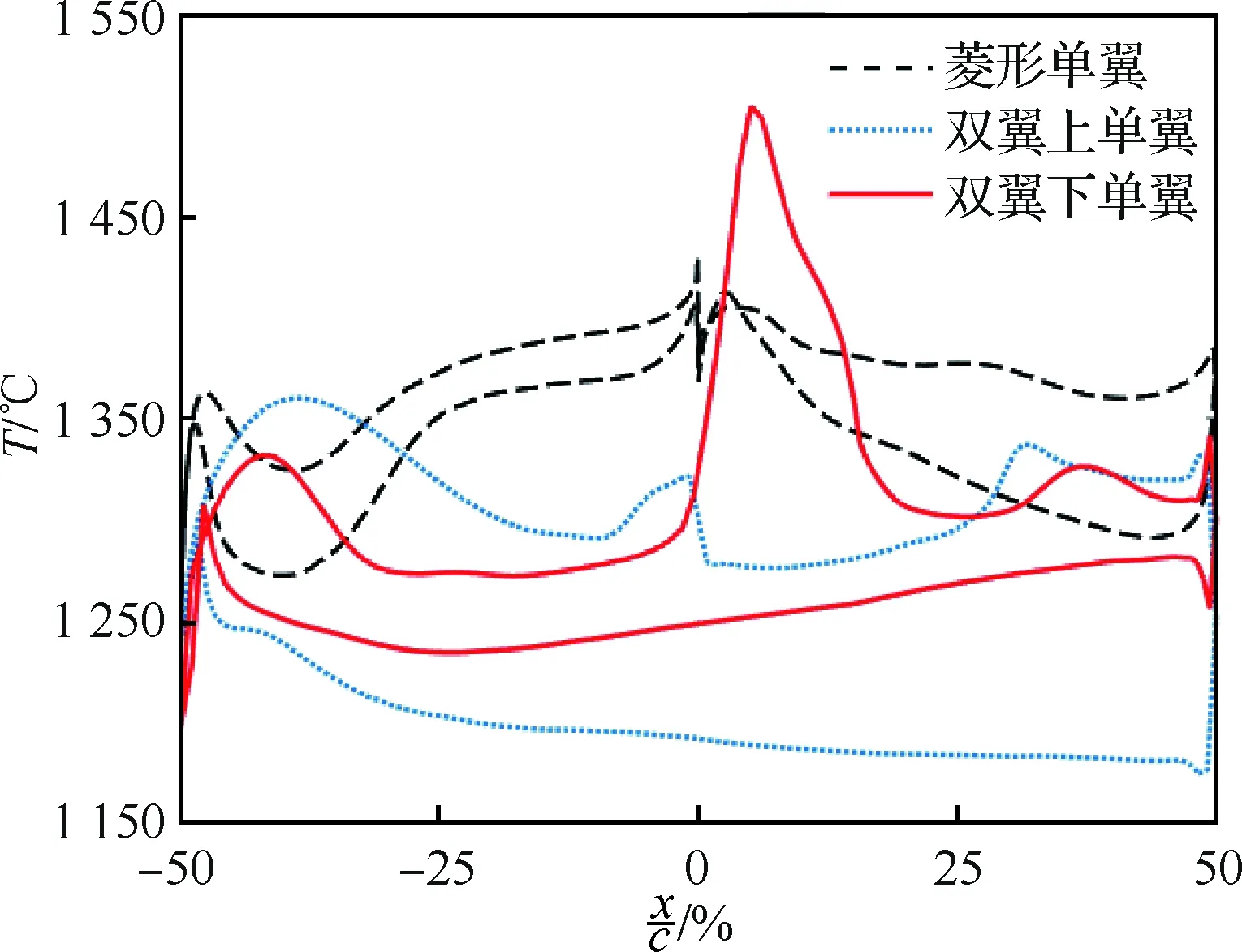
图24 机翼表面温度分布Fig.24 Temperature distribution of surface of wings

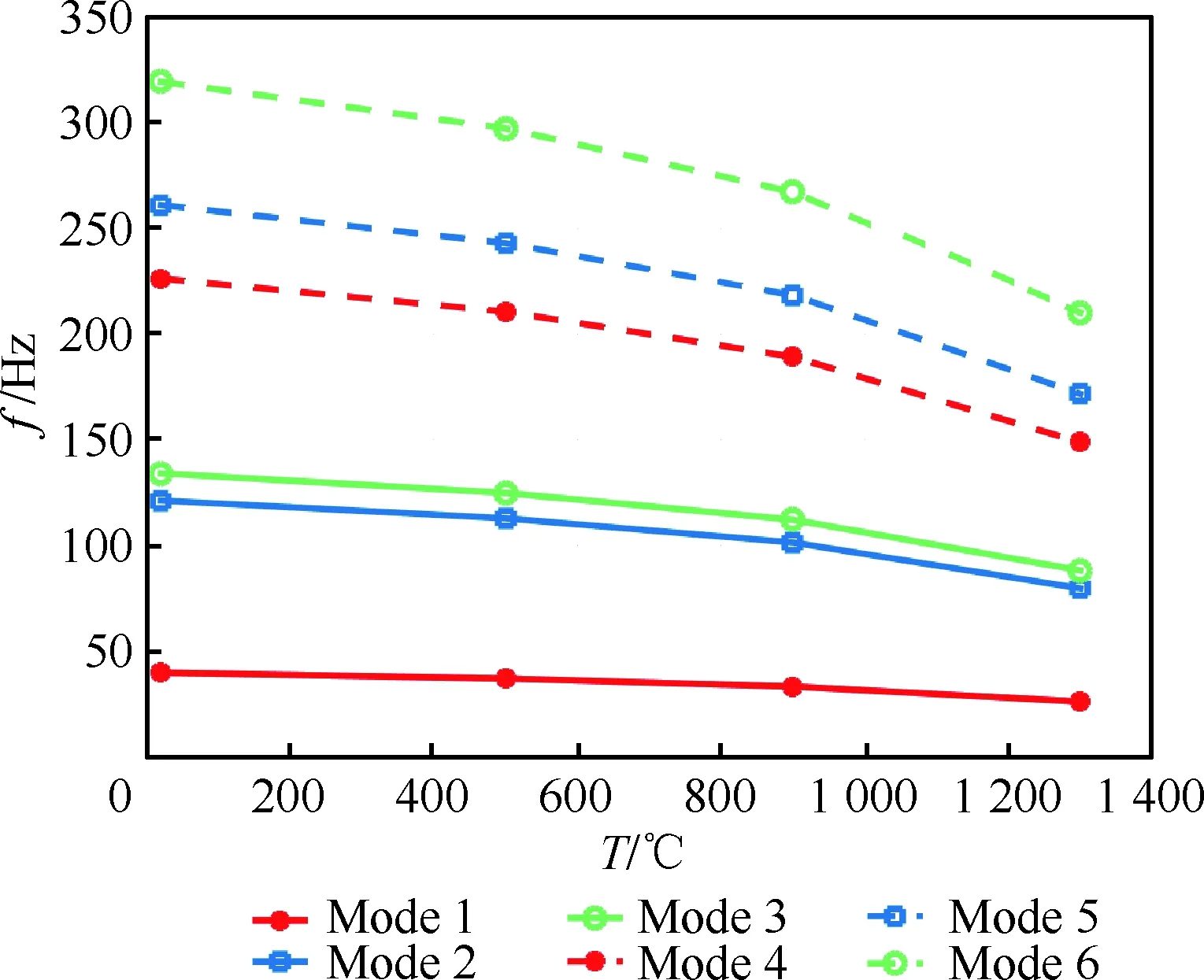
图25 温度对菱形单翼固有频率(前6阶模态)的影响Fig.25 Effect of temperature on natural frequency(first six modes) of diamond airfoil

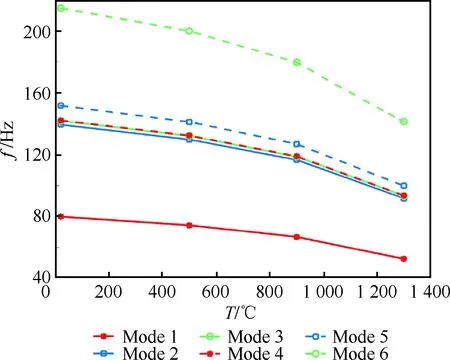
图26 温度对Busemann双翼固有频率(前6阶模态)的影响Fig.26 Effect of temperature on natural frequency(first six modes) of Busemann biplane

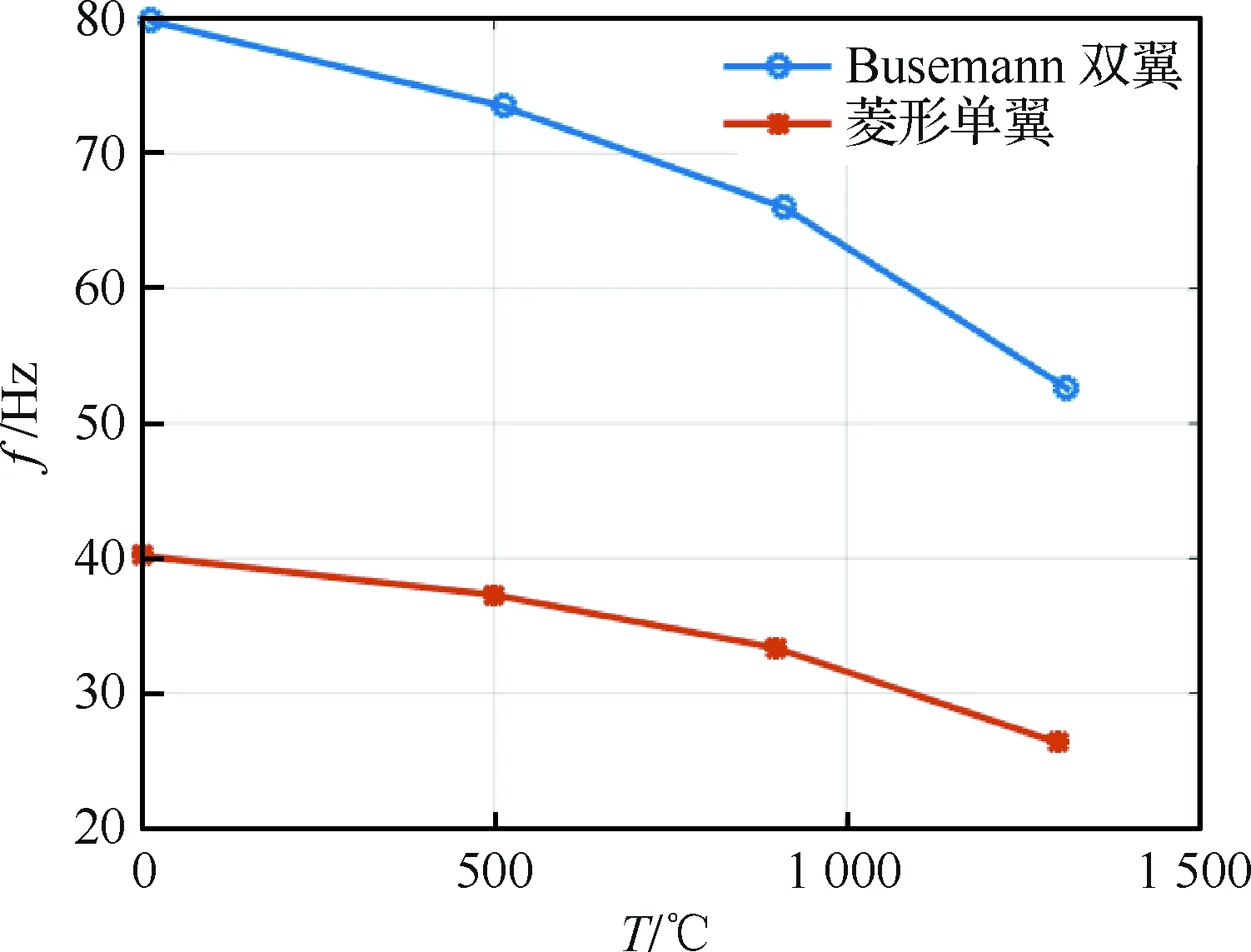
图27 温度对1阶模态固有频率的影响Fig.27 Effect of temperature on natural frequencies of the first order mode

从图27可以得到，在1 300 ℃时，相对于菱形单翼1阶弯曲模态的固有频率，Busemann双翼1阶弯曲模态的固有频率提高了99.8%，说明Busemann双翼具有更好的抗弯能力。

从20～1 300 ℃，Busemann双翼1阶弯曲模态的固有频率从79.88 Hz下降到52.58 Hz，下降了27.3 Hz；菱形单翼1阶弯曲模态的固有频率从39.97 Hz下降到26.31 Hz，下降了13.66 Hz，相对于各自在20 ℃时的固有频率，固有频率均下降了34.2%。可见温度对菱形单翼和Busemann双翼结构固有频率的影响很大，因此在高超声速飞行中不能忽略温度对Busemann双翼结构性能的影响。

5 结 论

为研究Busemann双翼翼型在高超声速机翼上的应用，本文构建了一种适用于高超声速飞行的Busemann双翼。

1) 推导出菱形单翼和Busemann双翼的升、阻力系数表达式，结合激波和膨胀波的干涉效应，从理论上证明了Busemann双翼能够提高升阻比。

2) 相对于菱形单翼，Busemann双翼能够明显提高升阻比。研究表明：相对于菱形单翼的升、阻力系数，Busemann双翼的升力系数提高了28.95%，阻力系数增大了13.58%，升阻比增加了13.74%，提高升阻比的效果较为明显。

3) 相对于菱形单翼，Busemann双翼能够减小翼尖涡强度。与菱形单翼翼尖上、下表面压力系数的绝对值均减小不同，Busemann双翼仅上单翼前缘的上表面和下单翼后缘的下表面的压力系数的绝对值有所减小，压力系数损失较小。

4) 基于Busemann双翼和菱形单翼升力相等的条件，Busemann双翼通过减小展弦比使其最小固有频率大于菱形单翼的最小固有频率，说明Busemann双翼具有更好的结构性能。

5) Busemann双翼和菱形单翼的表面温度最大值约在1 300 ℃左右，材料性能在此温度下发生变化。结果表明：相对于20 ℃时，此时Busemann双翼和菱形单翼一阶模态的固有频率均下降了34.2%，因此温度对结构性能的影响不能忽略。

通过对Busemann双翼在高超声速条件下提高升阻比的特性进行研究，并在考虑温度影响的情况下进行模态分析，表明Busemann双翼比菱形单翼具有更高的升阻比和更好的结构性能，在高超声速飞行器设计中将具有更广的应用前景和更高的实用价值。