传感器表面温度对热流测量的影响

曾磊，邱波，李宇，王安龄, *，桂业伟

1. 中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000 2. 中国运载火箭技术研究院 空间物理重点实验室，北京 100076

高超声速飞行器热环境的准确预测一直是国内外学者研究的重点。获得热环境数据的方法包括计算分析、地面试验和飞行试验。其中，地面试验和飞行试验数据一直是验证计算分析结果、确认防热设计数据的关键，特别是飞行试验中的热环境测量数据由于环境真实、无外加干扰而显得尤为珍贵。为此，美国、俄罗斯等国家多次开展了飞行试验，并开展了温度和热流的测量，相关数据为改进热环境计算分析方法和转捩预测方法提供了支撑[1-4]。中国空气动力研究与发展中心也开展了MF-1飞行试验任务，试验中测量了表面热环境、温度、压力等关键数据 。运载火箭研究院同样开展了高马赫数条件下飞行测热试验，获得了宝贵的热环境测量数据。

但是，在热流测量数据的处理和分析中，经常出现部分测量结果和前期预测结果存在一定偏差的现象，严重的甚至会导致对飞行器表面流态的误判。

在地面测热试验数据处理方面，国内外对热电阻类和热电偶类测热传感器都开展了大量的研究工作。Cook和 Felderman在1970年发布了基于一维半无限假设的Cook-Felderman公式，为薄铂膜类电阻温度计的热流处理提供了方法[5-7]。1994年，Matthews和Rhudy总结了高超声速风洞中的试验技术，回顾了众多的热流测量方法和热流传感器[8]。曾磊等[9-10]研究了风洞测热试验中存在的误差，并给出了一定的修正方法。但是，对于飞行试验中测热传感器数据处理方法的研究相对较少。

一般而言，高超声速飞行器外层防热结构多采用导热率较低的复合材料，而温度/热流传感器则多采用金属材料和大热沉式设计，这会导致测热传感器表面温度和周围机体表面温度存在较大差异。2017年，de Baar等[11]采用试验和计算方法研究了非均匀壁温下高超声速平板流动，发现壁温对边界层厚度和激波存在一定的影响，进而影响局部热环境。由此可见，传感器表面和机体表面的温度分布会对热环境分布和测量造成一定的影响。

本文针对传感器表面和机体表面温度差异较大的情况，设计了专门的计算模型和多个典型计算工况，获得了不同来流条件、不同壁温差异条件下传感器表面热流分布情况，为分析飞行条件下测热传感器热流测量数据提供了一种技术途径。

1 计算模型与来流条件

采用楔形平板作为计算模型，如图1所示。模型全长500 mm，前缘半径为5 mm，传感器位置(图1中黑点所示)处于计算模型中部距前缘300 mm处，传感器区域为直径10 mm的圆形。

图2给出了传感器安装示意图(图中q为进入传感器的热流，R为传感器半径)。飞行试验中传感器一般采用自研的同轴型铜-康铜热电偶形式。对于高超声速飞行器而言，通常飞行器外表面采用复合防隔热材料，其导热率较低，表面温升较快，而传感器采用的金属材料，具有导热快、热沉大、温升慢的特点。因此，详细考虑传感器与其周边温度的较大差异，对于获得准确的热环境测量数据是很有必要的。

图1 计算模型及物面网格示意图Fig.1 Diagram of calculation model and surface grids

图2 传感器安装示意图Fig.2 Diagram of sensor installation

本文计算的来流条件分别为：① 高度为54.7 km、马赫数为14、攻角为0 °、总焓约为10 MJ/kg；② 高度为50 km、马赫数为10、攻角为-15 °、总焓约为5.7 MJ/kg；③ 高度为50 km、马赫数为10、攻角为0 °、总焓约为5.7 MJ/kg。

本文计算的壁温条件分别为传感器表面温度为Ts=300,600,900,1 500 K，周边大面积表面温度To=300,600,900,1 200,1 500 K，采用了不同壁温的组合计算，以期获得影响传感器测量热流的关键因素。

2 计算分析方法简介

2.1 热环境计算方法

在笛卡儿坐标系下，守恒形式的三维非定常可压缩Navier-Stokes方程无量纲化后可写为

(1)

式中：Re为雷诺数；t为时间；Q为守恒状态变量；E、F、G为对流通量向量；Ev、Fv、Gv为扩散通量向量。

采用层流模型计算，其中黏性系数由Sutherland公式给出，采用完全气体假设，Prandtl数Pr=0.72，计算中取空气的比热比γ=1.4。

引入计算空间(ξ,η,ζ),使其与物理空间(x,y,z)存在唯一的单值坐标变换，其形式为

(2)

变换后的Navier-Stokes方程可以写为

(3)

本文采用有限体积法进行数值计算，因而可将控制方程式(3)写成积分形式,即

(4)

式中：f为封闭曲面S上的通量矢量；V为S包围的体积；n为S的单位法向矢量。将式(4)在网格线ξ、η、ζ包围的网格单元内积分，可得半离散化方程为

(5)

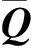
(6)

对于高雷诺数的定常黏性流动，为了准确模拟边界层，物面附近必须使用很小的网格间距。如果采用显式格式，如Runge-Kutta方法，将会因稳定性条件限制，使时间步长过小，以致必须花费大量的计算时间来收敛于定常解。因此对于Navier-Stokes方程的数值求解，本文采用Yoon提出的隐式LU-SGS(Low Upper Symmetric Gauss-Seidel)方法。对于半离散化方程式(5)，其采用LU-SGS方法可写为

(7)

式中：

(8)

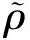
基于上述方法编写了自有计算软件，软件的有效性已得到了充分验证[12-14]。

2.2 热壁修正计算方法

高焓条件下的热壁修正方法为

(9a)

(9b)

式中：Qw为当地进入壁面的热流：Q300 K为当地300 K条件下进入壁面的热流；Hre为当地壁面外气流的恢复焓；Hw为当地壁面的焓值;H300 K为当地300 K条件下壁面的焓值。

通常，工程上用式(9a)计算变壁温条件下进入壁面的热壁热流值，或用式(9b)根据传感器测量结果反算300 K条件下的热流值。

3 计算结果与分析

3.1 结果与现象

图3 传感器表面热流随周边壁面温度的变化(传感器温度保持为300 K)Fig.3 Sensor surface heat flux as a function of surrounding wall temperature (sensor temperature remains 300 K)

本文首先计算了高度H=54.7 km、马赫数Ma=14、攻角α=0 °条件下，假设传感器保持300 K的温度不变，而周边防热材料的温度由300 K逐渐上升到1 900 K时传感器表面热流分布，并与300 K等壁温条件下的热流进行了比较，如图3所示。可见，虽然传感器本身的温度保持不变，但传感器表面的平均热流值随着周边防热材料壁温的升高而逐渐上升，由43 kW/m2上升到了124 kW/m2，上升幅度约为2.9倍。若测量分析人员认为测量得到的124 kW/m2为1 900 K条件下的热流值，再采用式(9b)进行修正，则换算得到的300 K条件下热流值约为145 kW/m2，为原有计算值的3.4倍左右。这会给对比热流预测数据、分析热流测量结果、判断当地流态带来极大的问题。

此外，如表1～表3所示，本文还计算得到了不同来流状态和不同温度条件下传感器表面的平均热流值Qave。从表1～表3可见，随着传感器周边温度的升高，传感器表面的热流值也在不断上升。从表1和表2比较来看，来流总焓对热流上升的幅值有较大影响；从表1和表3比较来看，来流攻角对热流上升的幅值也有一定影响。

图4给出了不同来流条件和不同壁温条件下传感器及其周边区域热流(Qw)的分布。可见，在相同壁温条件下，传感器区域和周边区域热流分布光滑一致；在不同壁温分布的情况下，传感器表面热流与周边热流存在着明显的差异。

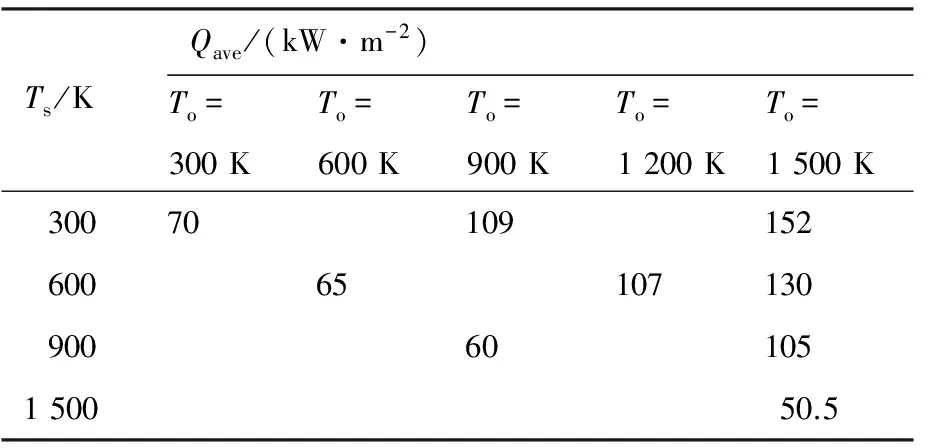
表1 传感器表面平均热流(H=50 km，Ma=10，α=-15 °)Table 1 Average heat flux on sensor surface(H=50 km，Ma=10，α=-15 °)

表2 传感器表面平均热流(H=54.7 km，Ma=14，α=0 °)Table 2 Average heat flux on sensor surface(H=54.7 km， Ma=14，α=0°)

表3 传感器表面平均热流(H=50 km，Ma=10，α=0 °)Table 3 Average heat flux on sensor surface(H=50 km， Ma=10，α=0°)

图4 不同条件下传感器及其周边区域热流分布Fig.4 Heat flux distribution of sensor and its surrounding area under different conditions

3.2 成因及分析

为了更好地分析表面温度差异对传感器表面热环境分布的影响，本文详细研究了传感器“冷点”对其局部周边热环境的影响，结果如图5和图6所示。

图5 相同周边壁面温度、不同传感器温度下传感器表面热流分布Fig.5 Distribution of heat flux on sensor surface with different sensor temperatures and same surrounding wall temperature

图6 相同传感器温度、不同周边壁面温度下传感器表面热流分布Fig.6 Distribution of heat flux on sensor surface with same sensor temperature and different surrounding wall temperatures

由图5可见，在周边温度相同的情况下，两者之间的温度差异越大，传感器表面的热流值越大，且传感器表面热环境呈“月牙”型分布，即整体沿来流方向逐步降低、越靠近周边高温区热流越大。

图6给出了相同传感器温度、不同周边壁面温度下传感器区域表面热环境分布情况，整体分布规律与图5反映的现象相同。

从过增元等提出的场协同理论[15-16]来看，热流是气体换热能力的表征，热流大小与当地法向速度和法向温度梯度密切相关，即法向温度梯度越大、法向速度越大则换热越剧烈。为了分析传感器表面热环境增加的机理，本文提取了传感器中心线上距传感器前缘x=0.2 mm处法线上的温度分布和速度分布，分别如图7～图9所示，图8和图9中δT/δn为法向温度梯度。

图7 不同攻角下传感器前端(x=0.2 mm)处的法向温度和速度比较Fig.7 Comparison of normal temperature and velocity of sensor front end (x=0.2 mm) at different angles of attack

图8 不同温差下传感器前端(x=0.2 mm)处的法向温度和速度比较Fig.8 Comparison of normal temperature and velocity of sensor front end (x=0.2 mm) with different temperature differences

图9 相同温差下传感器前端(x=0.2 mm)处的法向温度和速度比较Fig.9 Comparison of normal temperature and velocity of sensor front end (x=0.2 mm) with same temperature difference

由图7可见，在传感器和周边壁面均为300 K条件下，法线上的温度变化较小，且法向速度很小(指向壁面为负)；当周边壁面温度逐渐上升至900 K、1 500 K，法向上的温度梯度逐渐变大，且近壁面处的法向速度逐渐增大。本文认为法向速度增大是由于传感器处温度降低导致局部压力减小而产生的局部细微流动；温度梯度增大是由于边界层内的气体温度已随周边壁面温度的上升而上升，当边界层发展到局部低温区域时，近壁面处的温度梯度将急剧增大。这些现象[17-18]导致了传感器前端热流的升高。

同样，相同流速和马赫数下，攻角的增大导致迎风面激波强度的增加，也增大了边界层内的温度梯度和法向速度，导致了热流的整体升高。

为了进一步研究影响局部热流升高的敏感因素，本文计算分析了相同来流状态下，不同壁面温度但相同温差条件下的热环境分布，由表1可见，相同来流状态下相同温差(ΔT)导致的传感器表面热流升高幅度(ΔQave)相近，这说明在相同总温条件下，ΔQave与ΔT密切相关。图8给出了不同温差下传感器前缘0.2 mm法向上的温度和速度分布情况，图9给出了相同温差下传感器前缘0.2 mm法向上的温度和速度分布情况。可见当温差相同时，法向温度梯度和速度的差异均远远小于不同温差的情况。

图10 传感器中心线上不同位置处的法向温度和速度比较Fig.10 Comparison of normal temperature and velocity of sensor center line at different positions

图10给出了传感器中心线上不同位置处法向速度和温度分布。从图中可见，大温差条件下即使在传感器中部和后部区域法向温度梯度也比传感器和周边壁面均为300 K条件下大得多，传感器中部存在着较小的向下流动速度；而传感器后部由于靠近高温壁面，局部压力上升所以存在着一定的向上流动趋势，导致热流略有下降，但由于大温度梯度的存在，传感器后部区域的热流仍高于周边高温壁面。

4 结 论

1) 当传感器和周边材料的温度存在一定的差异时，导致了该区域近壁面流场中的压力、密度等特征量梯度增大，改变了传感器当地的法向速度和温度分布，造成了局部热流的剧烈变化。因此，在实际测热试验当中，需综合考虑传感器材质和周边防热材质的不同，通过分析和计算修正测热结果，以免造成对当地热流的误判。

2) 相同来流马赫数和高度下，来流攻角主要影响法向速度的分布，从而影响气动加热量，攻角越大，相同温差下加热量上升的幅度越小；来流总温主要影响法向温度梯度的分布，从而影响气动加热量，来流总温越大在相同温差条件下加热量上升幅度越小。

另外，本文的研究还存在一定的不足，下一步还将在如下两部分开展深入研究。

1) 传感器表面存在着热流分布，会造成一定的温度分布，而传感器的测热敏感部位感受到的热流是当地温度下反映得到的热流，并非本文所给出的平均热流。这就需要开展沿弹道下的传感器及其周边区域的气动热/传热耦合计算，以便和真实试验情况相互比较。

2) 当来流马赫数在15以上时，来流总温进一步提高，空气离解现象加剧，真实气体效应明显。目前，C/SiC类防热材料的催化复合系数大多为0.01以下，而传感器一般采用的铜/康铜类热电偶材料的催化复合系数接近完全催化。因此，大量的高能粒子会在传感器上发生复合反应，从而进一步增大传感器表面的热流。这也是在高马赫数下传感器热环境测量数据分析中必须考虑的一个问题。

致 谢

感谢中国运载火箭研究院的曹占伟研究员对本论文研究内容的支持，在讨论中给予本项目研究方向提出了宝贵的建议。感谢中国空气动力中心的代光月博士和刘深深硕士，在具体计算方案的讨论中迸出的思想火花。感谢中国空气动力研究与发展中心飞行器热安全课题组对本项目的大力支持和计算条件保障。