基于有限元法的高速圆柱滚子轴承热特性分析

马志涛，李军宁，赫东锋，刘波，张君安

（西安工业大学 机电工程学院，西安 710021）

轴承内、外圈及滚动体材料一般为高碳铬轴承钢（GCr15等）或渗碳轴承钢（G20Cr2Ni4A等），热处理后硬度不低于60 HRC，通常轴承的工作温度不高于120℃时，零件的硬度不会下降[1]。随着现代机械设备转速向高速化发展，滚动轴承热问题愈来愈严重，若在稳态工作状态下，轴承内的摩擦热不能及时有效地散发，系统的温度将不断上升直到润滑失效，最后导致轴承提前失效。轴承摩擦热的计算，国内外学者应用最多的是Pamlgren和Harris提出的滚动轴承发热量计算方法[2-3]。Palmgren发热量计算模型简单易算，但适用于中等载荷和中等转速条件；Harris整 体计算方法是在Palmgren基础上通过试验修改得出。Harris局部计算热量方法考虑了滚动轴承摩擦的6大因素[4]，但是计算繁琐，需要开发计算机程序来分析轴承的动力学参数，然后联立其提出的局部计算轴承部件摩擦热计算公式，得出轴承零件的温度分布。

文中对国内外学者提出的滚动轴承热量计算方法进行对比分析，选出更适合计算滚动轴承发热的方法，然后在此基础上应用 ANSYS Workbench建立热分析模型，研究了润滑油运动黏度和转速对轴承发热的影响。

1 滚动轴承发热量计算方法对比

滚动轴承发热量整体法计算是指滚动轴承的总摩擦力矩与套圈转速相乘得到的发热量经验公式，常见的方法有：近似法、Pamlgren法、Astridge法[5]以及 Harris，B M捷米道维奇等提出的方法[6]，这些方法均将滚动轴承整体作为研究对象在试验基础上得到发热量计算公式。Astridge在Palmgren的计算公式和试验基础上提出了圆柱滚子轴承摩擦发热的经验计算公式，此公式适用于润滑流量大和转速较高工况下的圆柱滚子轴承。B M捷米道维奇在理论和试验的基础上提出了高速圆柱滚子轴承发热量的经验计算公式，但没有考虑轴承零件间的接触对摩擦生热的影响[4]。近似法是与载荷有关而与转速无关的经验公式，只适合低速运转轴承的粗略计算。

滚动轴承发热量局部法计算是指对滚动轴承各零件单独计算每个接触单元间的局部摩擦热。Harris考虑了滚动体与滚道的摩擦发热、滚动体产生的搅油功率损耗、保持架与内外圈引导面的摩擦生热、滚子与保持架兜孔的摩擦发热、滚子端面与套圈挡边的摩擦发热等，提出了滚动轴承摩擦发热的局部计算方法。Rumbarger[7]等人也提出了一种计算滚动轴承摩擦热的局部计算方法，建立了流体牵引力矩模型，分别计算了滚子、保持架和内外圈滚道产生的功率损失，模型假设轴承内部各零件在黏性流体内部以一定角速度旋转的圆柱体[8]。

现以NU209型外圈双挡边、内圈无挡边圆柱滚子轴承为例，选取润滑油运动黏度为15 mm2／s，分别应用近似法发热量计算模型、Palmgren发热量计算模型、Astridge发热量计算模型、Rumbarger发热量计算模型、Harris整体法发热量计算模型和B M捷米道维奇发热量计算模型进行对比分析。圆柱滚子轴承NU209结构参数见表1，内圈旋转，外圈固定。不同计算模型下，轴承摩擦功率损失与转速的关系见表2（Fr＝2 kN，Fa＝0）。

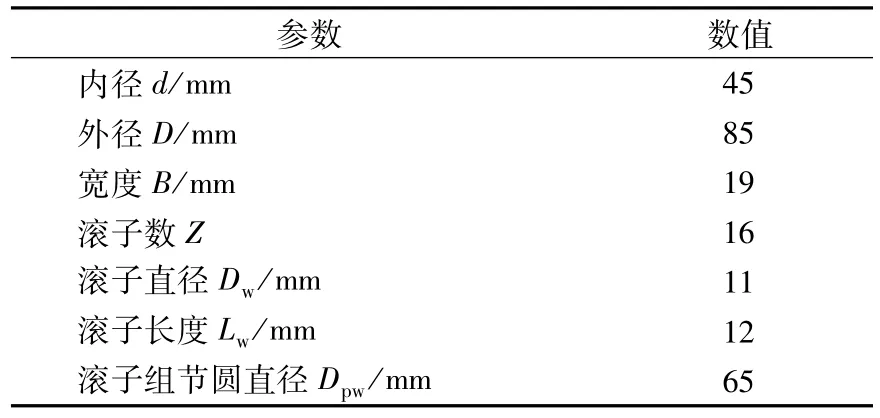
表1 圆柱滚子轴承NU209结构参数Tab.1 Structural parameters of cylindrical roller bearing NU209

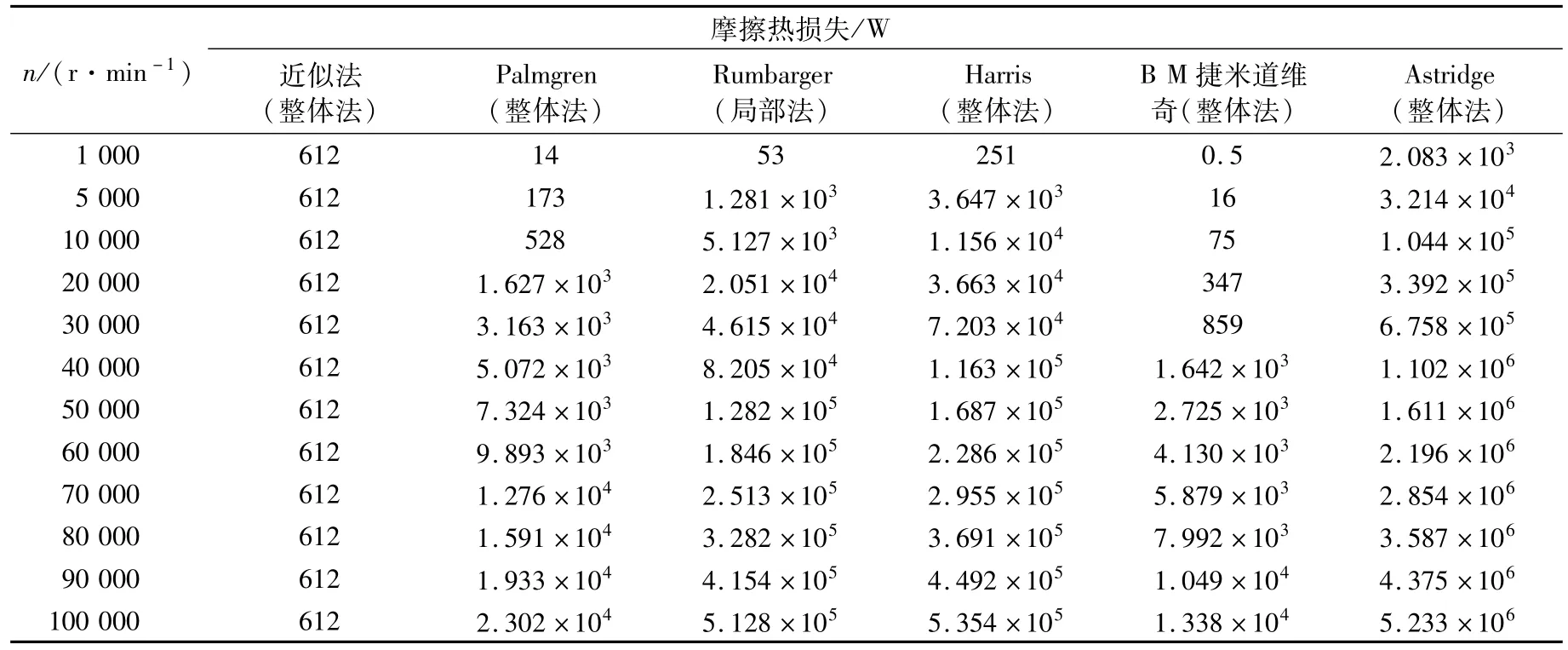
表2 摩擦热损失与内圈转速的关系Tab.2 Relation between frictional heat loss and rotational speed of inner ring

由表2数据可知：在相同转速下，Astridge（整体法）计算轴承摩擦功率损失热量是最大的，并且随着转速的增加热量增加也是最大的；近似法计算公式与转速无关，只与载荷有关，所以在相同载荷下，随着转速的增大，轴承热量损失不变，这种方法适合低速工况下轴承热量的粗略计算，不适合高速滚动轴承；在同一径向载荷下，随着轴承转速的增加，Rumbarger（局部法）和Harris（整体法）计算出的滚动轴承摩擦功率损失越接近；Palmgren（整体法）和B M捷米道维奇法（整体法）功率损失计算结果大致在同一数量级。

2 滚动轴承热特性分析

通过对滚动轴承发热量计算方法的对比分析可知，Rumbarger局部法和Harris整体法滚动轴承摩擦功率损失在高速下最接近，在相同条件下，其计算结果介于其他计算方法数值的最大值和最小值之间。Rumbarger等人利用所建立的流体牵引力矩模型提出轴承各部分产生的局部摩擦功率损失，但并未见其对测试结果与计算结果进行对比分析。现采用 Rumbarger计算模型和 ANSYS Workbench相结合对圆柱滚子轴承系统进行热特性研究。

2.1 Rumbarger法轴承发热计算模型

Rumbarger提出在黏性流体介质中，以角速度ω旋转的圆柱表面的功率损失[7]为

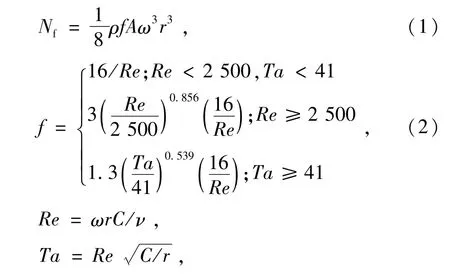
式中：ρ为润滑油密度；f为摩擦因数；A为圆柱表面有效面积；ω为圆柱体旋转角速度；r为圆柱体半径；Re为Reynolds数；Ta为Taylor数；C为圆柱表面周围的特征间隙；ν为润滑油运动黏度。

将此模型分别应用在内圈滚道表面、滚子表面、保持架表面上就可定量计算出滚动轴承系统内各零件表面的功率损失。

2.2 Rumbarger法轴承传热计算模型

滚动轴承系统中存在的散热形式有热传导、热对流和热辐射，主要考虑对流换热[8]。高速滚动轴承大多数采用喷油润滑方式，轴承系统对流换热主要为润滑油与内外圈滚道表面的对流换热、润滑油与滚动体表面及保持架的对流换热、轴承座外表面与空气对流换热，其对流换热系数计算如下：

1）对于外圈固定，内圈旋转，内、外圈与保持架圆柱表面之间流体的对流换热系数[7]为

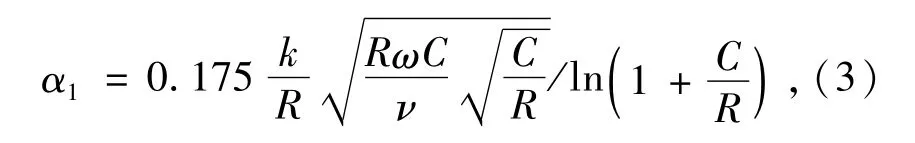
式中：k为润滑油导热系数；R为内滚道半径。

2）轴承座外表面与流体（空气）之间的自然对流换热系数[7]为

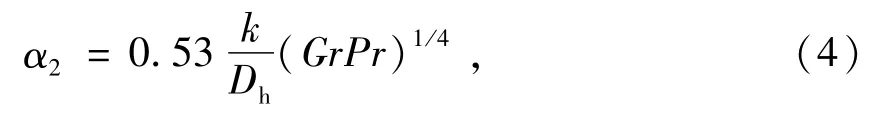
式中：Dh为轴承座圆柱表面直径；Gr为Grashof准则；Pr为Prandtl准则。

3）润滑油与滚动体的受迫对流换热系数[9]为

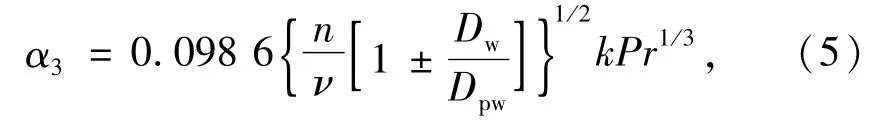
式中：Dw为滚动体直径；Dpw为滚子组节圆直径。

4）润滑油与旋转轴外表面之间的受迫对流换热系数[9]为

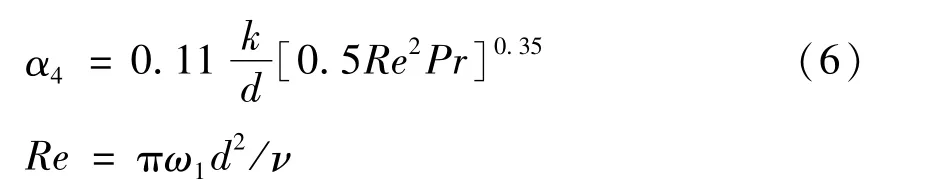
式中：ω1，d分别为轴的角速度和直径。

2.3 有限元法轴承热分析模型

ANSYS Workbench热分析模块基于能量守恒的热平衡方程。在有限元软件热分析中，提供了6种热载荷（温度、热流率、对流、热流密度、生热率和热辐射率），这些载荷可以施加在实体模型或单元模型上，对于既有对流换热又有摩擦热的边界，需要使用ANSYS中的表面效应单元SURF151来施加2种以上的边界条件[10]。

3 方法验证

为了验证Rumbarger局部法轴承热计算方法是否与实际结果相符，使用文献[11]的轴承作为算例进行有限元法分析，然后与文献[11]结果进行对比。文献[11]采用的是移动热源法，文中采用Rumbarger局部法计算时的几何分析模型、轴承材料、润滑油、网格划分和边界条件加载等均与文献[11]相同。

外圈固定，内圈转速为16 000 r／min，径向载荷2 kN，入口油温60℃下，采用有限元计算出的圆柱滚子轴承系统温度分布如图1所示。

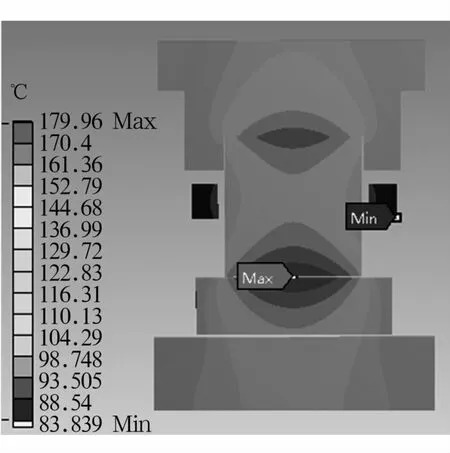
图1 轴承零件温度分布Fig.1 Temperature distribution of bearing parts

Rumbarger局部法轴承热量计算模型得到温度分布（最高温度179.96℃，最低温度84.7℃）与文献[11]得到的结果（最高温度185.6℃，最低温度83.8℃）相近，2种算法最高温度和最低温度部位都分别出现在内圈滚道和保持架。由于文献[11]结果是经过试验验证的，因此，也验证了Rumbarger局部法轴承热量计算模型的正确性和有效性。

4 建模及结果分析

4.1 建模

仍以NU209圆柱滚子轴承为例，表1给出了轴承主要结构参数；轴承材料选用GCr15轴承钢，当温度为100℃时，导热系数k′＝45W／m·℃；给定轴承转速 n＝20 000 r／min，径向载荷 Fr＝2 kN，轴向载荷 Fa＝0，润滑油的导热系数 k＝0.14 W／m·℃，入口油温60℃。在ANAYS Workbench软件中设置 Sizing的 Relevance Center为 Fine，其余采用默认设置，建立NU209圆柱滚子轴承模型如图2所示。

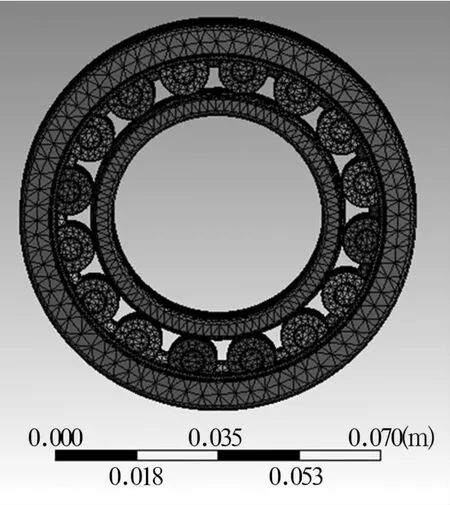
图2 轴承有限元模型Fig.2 Finite element model of bearing

采用Rumbarger局部法计算NU209轴承各部件摩擦发热量，并计算轴承零件与润滑油间的对流换热系数；然后在ANSYS Workbench界面输入轴承材料参数、热流密度和传热边界条件后，可以分析出轴承零件的温度场分布。

4.2 转速对轴承温度分布的影响

外圈固定，内圈旋转，径向载荷2 kN，入口油温度60℃下，转速对轴承温度的影响如图3所示。由图可知，最大温升为内圈滚道，外圈滚道温度和滚子表面温度在相同转速下数值相近，保持架温度变化小。转速为30 000 r／min时，内圈滚道温度达到225℃，外圈滚道和滚子表面温度达到190℃左右；当转速为40 000 r／min时，已严重超出NU209轴承的极限转速，轴承零件温度发生剧增，计算结果失真。

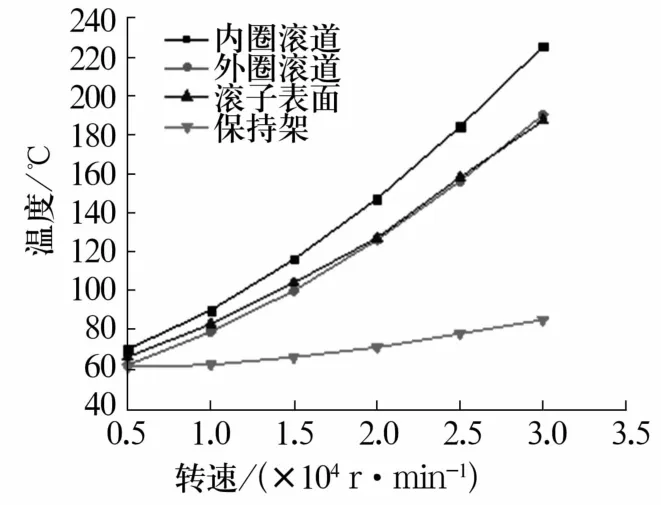
图3 转速对轴承各零件温度的影响Fig.3 Influence of rotational speed on temperature of bearing parts

4.3 润滑油黏度对轴承温度分布的影响

外圈固定，转速为 20 000 r／min，径向载荷Fr＝2 kN，轴向载荷Fa＝0下，润滑油运动黏度对轴承各零件温度的影响如图4所示。由图可知，运动黏度的微小变化对轴承零件的温度影响很大，润滑油运动黏度从1 mm2／s增加到1.8 mm2／s，内圈滚道温度从113℃上升到183℃。因此，选取合适的润滑油极为重要，在满足润滑质量条件下，高速轴承应尽量选取低运动黏度的润滑油。

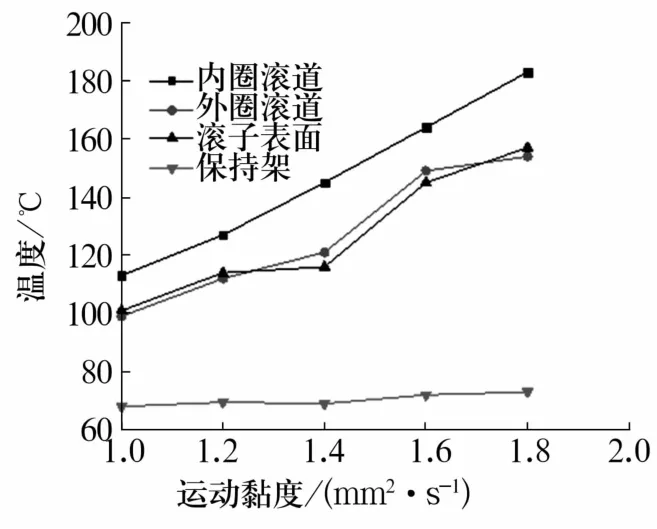
图4 润滑油运动黏度对轴承零件温度的影响Fig.4 Influence of viscosity of lubricating oil on temperature of bearing parts

5 结论

通过详细对比分析滚动轴承摩擦热的6种主要计算方法，研究了不同转速和不同运动黏度作用下NU209圆柱滚子轴承工作时的温度分布，可以得出以下结论：

1）Rumbarger局部法理论计算和有限元软件相结合分析出滚动轴承温度分布与文献[11]结果比较一致，该模型应用于高速滚动圆柱滚子轴承热分析具有正确性和有效性，验证了内圈滚道表面因温度过高而最先失效。

2）润滑油运动黏度的微小变化对轴承零件温度影响很大，运动黏度每增加0.2 mm2／s，内圈滚道温度升高18℃。随着润滑油运动黏度增加，轴承内圈滚道、外圈滚道、滚子表面和保持架温度均增加，内圈滚道增加最大。在满足润滑质量前提下，应尽量选取低运动黏度的润滑油。