如何求解古典概型的概率
福建
吴志鹏
(作者单位:福建省泉州市德化第一中学)
如何求解古典概型的概率
福建
吴志鹏
古典概型是学生学习概率与统计的起点,是一种重要的概率模型.
一、古典概型的两个基本特征
1.所含的基本事件个数有限;
2.每个基本事件的发生都是等可能的.
二、解决古典概型概率的基本步骤
1.分析具体问题确定样本空间;
2.确定样本空间包含的基本事件的总数n;
3.确定事件A所包含的不同基本事件的个数m;
三、样本空间的选择
1.正确选取样本空间:要保证所选取的样本空间所含基本事件个数是有限的,且等可能发生.
【例1】先后掷两枚骰子,求向上点数和为奇数的概率.

【例2】射击运动员向一靶心进行射击.试验的结果为:命中10环,命中9环,……,命中0环,求其命中8环以上的概率.
因为命中10环,命中9环,……,命中0环不是等可能的.因此并非古典概型,不能用古典概型的概率公式求解.
2.样本空间的选取是相对的而非绝对的
【例3】(2016·全国卷Ⅰ文·3)为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是
( )
【答案】C
分析:对于样本空间的选取可分为以下两种方案:


两种方案所选取的样本空间是不一样的,但结果却都是正确的,这说明基本事件总数与所研究事件包含的基本事件数必须在同一样本空间中考虑,其结果也是相同的,因此样本空间的选择是相对的而非绝对的.
四、样本点的计数
1.对于样本空间所包含的基本事件(样本点)总数比较少时,对样本点的记数可采用枚举法或树状图进行表示,对于事件A所含的样本点可从所罗列的图表中标记获得,直观而具体,但应把握列举的原则,不要出现重复和遗漏.
【例4】(2017·全国卷Ⅱ文·11)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
( )
解:法一,利用树状图可以列出,从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,所有可能结果:
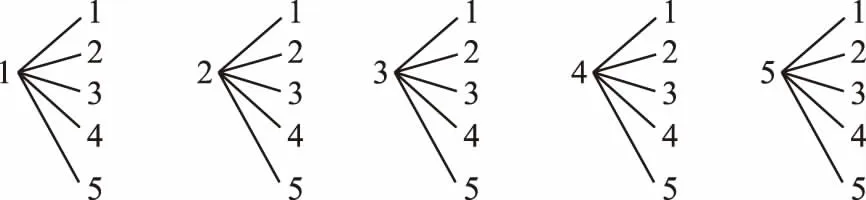


2.对于样本空间所包含的基本事件(样本点)总数比较多时,用树状图或列举法罗列样本点比较困难,需通过排列组合或利用加法原理与乘法原理求得.
(1)排列与组合:

②有放回的选取:从n个不同的元素中取出r个不同的元素进行排列,总数有nr种.
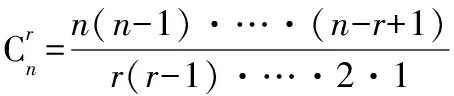

(2)两条原理:
加法原理:做一件事,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,那么完成这件事共有N=m1+m2+…+mn种不同方法.每一种方法都能够直接达成目标.
乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1·m2·…·mn种不同的方法.
【例5】如图,在一个木制的棱长为3的正方体表面涂上颜色,将它的棱3等分,然后从等分点把正方体锯开,得到27个棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.

(1)从这个口袋中任意取出1个小正方体,这个小正方体的表面恰好没有颜色的概率是多少?
(2)从这个口袋中同时任意取出2个小正方体,其中1个小正方体恰好有1个面涂有颜色,另1个小正方体至少有2个面涂有颜色的概率是多少?
分析:该模型为古典概型,基本事件个数是有限的,并且每个基本事件的发生是等可能的.题目(2)所涉及的基本事件总数比较多,所求事件中的基本事件的构成比较复杂,既要分类又要分步,融合了两个原理及排列组合,因此学习时要注意理解原理并要掌握排列组合的方法.
【解】在27个小正方体中,恰好3个面都涂有颜色的共8个,恰好2个面涂有颜色的共12个,恰好1个面涂有颜色的共6个,表面没涂颜色的1个.
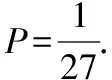
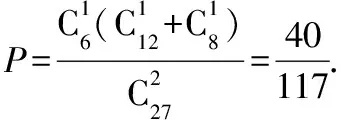

五、从古典概型具体问题中抽出的三个基本模型
1.随机取数模型:从多个数字中任取一个,每个数字被取到的可能性相同.分为重复取得和不重复取得两种情况.
【例6】(2016·全国卷Ⅲ文·5)小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是M,I,N中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是
( )
【答案】C
【例7】(2015·全国卷Ⅰ文·4)如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为
( )
【答案】C
分析:例6可转化为两次分别从3个和5个不同的数字中不放回地随机取出1个不同的数进行求解,例7则转化为从5个不同的数字中不放回地随机取出3个不同的数进行求解.
2.摸球问题:袋中有多种外形完全相同、颜色不同的球,现从袋中任取一球,任一球被摸到的可能性相同,分有放回和无放回的抽取两种情况.
【例8】已知一个口袋有m个白球,n个黑球(m,n∈N*,n≥2),这些球除颜色外全部相同.现将口袋中的球随机逐个取出,并放入如图所示的编号为1,2,3,…,m+n抽屉内,其中第k次取出的球放入编号为k的抽屉(k=1,2,3,…,m+n).

123…m+n
试求编号为2的抽屉内放的是黑球的概率P.

3.分信问题:n封不同的信等可能的被投到N个信箱中.
【例9】(2017·山东卷文·16改编)3名旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择1个国家去旅游.
(1)这3名旅游爱好者有多少种旅游方案可供选择?
(2)若3名旅游爱好者从这6个国家中任选2个去旅游,求这2个国家都是亚洲国家的概率?
分析:(1)本题可转化为将3封不同的信投到6个不同的信箱,则有6×6×6=216种;

(作者单位:福建省泉州市德化第一中学)

