“超级全能生”2018年高考全国卷26省3月联考甲卷数学(文科)

“超级全能生”2018年高考全国卷26省3月联考甲卷数学(文科)

一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1.已知全集U=R,集合A={x|2x-4>0},B={x|2x<8}，则集合U(A∩B)=

( )

A.(-∞,2] B.[3,+∞)

C.(-∞,2]∪[3,+∞) D.(-∞,2)∪(3,+∞)

( )

A.-1-i B.1-i C.-1±i D.±1-i

3.在边长为4的等边三角形内随机取一点，则此点取自该三角形的内切圆内的概率是

( )

4.执行如图所示的程序框图，则输出的结果为

( )

A.380 B.381

C.420 D.421

5.已知向量a,b都是非零向量，则“|a|+|b|=|a+b|”是“a与b方向相同”的

( )

A.充要条件 B.充分不必要条件

C.必要不充分条件 D.既不充分也不必要条件

( )

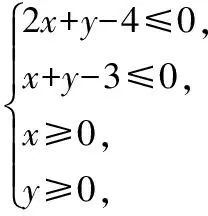
A.6 B.7 C.8 D.9

( )

A.-2 B.-4 C.-6 D.-8

8.《九章算术·商功》中记载：“斜解立方，得两堑堵.斜解堑堵，其一为阳马，一为鳖臑.”其意：“取一长方体，沿对角面分割，可得两个一模一样的堑堵，再沿堑堵的一顶点与其相对的棱剖开，得阳马和鳖臑(阳马是一棱与底面垂直的四棱锥，鳖臑是四个面为直角三角形的三棱锥).”今有一堑堵分割后得阳马和鳖臑，且鳖臑的三视图如图所示，若图中网格中小正方形的边长为1，则此堑堵分割后得到的阳马的体积是

( )

A.12 B.8 C.4 D.2

( )

A.x-y+1=0

B.2x-y=0或x+y-3=0

C.x+y-3=0

D.x-y+1=0或x+y-3=0

( )

11.某商场有3个入口，分别为A，B，C，今有甲、乙、丙、丁四人分别从这三个入口进入该商场，每个入口至少一人进入.现有如下情况：①甲必从A进入；②若乙从B进入，则丙不单独进入；③丁必不从C进入.根据以上情况，四人进入该商场的方法有

( )

A.4种 B.5种 C.6种 D.7种

12.已知函数g(x)=4e(lnx)2-(2em+4)x|lnx|+2mx2，则关于x的不等式g(x)<0恰只含有一个整数解，则实数m的取值范围是

( )

二、填空题：本题共4小题，每小题5分，共20分.

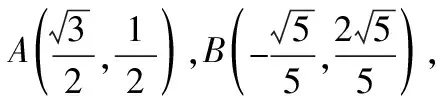
14.已知一个侧面积为16π，母线长为4的圆柱，其上、下底面圆都在球O的表面上，则球O的表面积是________.

三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答.

(一)必考题:共60分.

17.(12分)

已知数列{an}的前n项和为Sn(n∈N*)，若a1=2，an+1=2an(n≥2)，且S3=5.

(Ⅰ)求an和Sn；

18.(12分)

某网络大型外卖平台为了调查旗下的“骑手”获“五星好评”是否和性别有关，该平台的调查部门从某市在同一时段内通过该平台订餐的客户的评价中，随机抽取出120条评价信息.统计如下表：

获“五星好评”未获“五星好评”总计对男“骑手”的评价a1260对女“骑手”的评价56b60总计c16120

(Ⅰ)计算表中的a，b，c的值，并判断是否有95%的把握认为获“五星好评”和性别有关？请说明理由；

附参考公式及参考数据：

P(K2≥k0)0.1000.0500.0250.010k02.7063.8415.0246.635

19.(12分)

如图，在四棱锥P-ABCD中，底面ABCD为矩形，且AD=PD=1,AB=PB=2.

(Ⅰ)连接BD，求证：PA⊥BD;

(Ⅱ)若H在CD上，且PH⊥平面ABCD,求线段PH的长度.

20.(12分)

(Ⅰ)求椭圆Γ的方程；

21.(12分)

(Ⅰ)求函数f(x)在点(0,f(0))处的切线方程；

(Ⅱ)若函数f(x)在R上单调递增，求实数a的取值集合.

(二)选考题：共10分．请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题记分.

22.[选修4—4：坐标系与参数方程](10分)

在直角坐标系xOy中，曲线C1:(x-2)2+y2=3．在以原点为极点，x轴正半轴为极轴的极坐标系中，曲线C2:ρsin2θ=4cosθ．

(Ⅰ)求出C1的极坐标方程和C2的直角坐标方程；

23．[选修4-5：不等式选讲](10分)

已知函数f(x)=|x+1|-|2x+1|+1，且函数f(x)的最大值为m.

(Ⅰ)求m的值；

(Ⅱ)若存在x,y∈R，使得不等式2m-|x2-2y+1+a|≥|y2-4x+4+b|(a,b∈R且a+b>0)成立，求a+b的取值范围．

参考答案

17.解:(Ⅰ)由an+1=2an(n≥2)，可得该数列是从第二项起公比为2的等比数列，

又S3=5，a1=2，所以a2+a3=3，

(1分)

又a3=2a2，即可得a2=1，

(2分)

则an=a2qn-2=2n-2(n≥2)，

(3分)

当n=1时，Sn=a1=2；

(4分)

(5分)

且S1=2适合上式，综上所述,Sn=2n-1+1.

(6分)

(8分)

(10分)

(11分)

(12分)

18.解:(Ⅰ)由a+12=60,56+b=60,c+16=120，

解得a=48,b=4,c=104，

(2分)

则K2的观测值

所以有95%的把握认为获“五星好评”和性别有关.

(6分)

(Ⅱ)由题意可知,未获“五星好评”的评价中，有4条是对男“骑手”的“四星评价”， 有2条是对女“骑手”的“四星评价”，共计6条“四星评价”，

(7分)

设对男“骑手” 的“四星评价”的4条信息分别为A1，A2，A3，A4,对女“骑手” 的“四星评价”的2条信息分别为B1，B2，

任取2条有{A1，A2},{A1，A3},{A1，A4},{A1，B1}，{A1，B2}，{A2，A3},{A2，A4},{A2，B1}，{A2，B2}，{A3，A4},{A3，B1}，{A3，B2}，{A4，B1}，{A4，B2}，{B1，B2}，共15种不同的选法，

(9分)

其中对男、女“骑手”的“四星评价”各有1条信息的有

{A1，B1}，{A1，B2}，{A2，B1}，{A2，B2}，{A3，B1}，{A3，B2}，{A4，B1}，{A4，B2}，共8种不同的选法，

(11分)

(12分)

19.解：(Ⅰ)证明：取AP的中点为E，连接DE,BE,

由DA=DP,BA=BP，可得DE⊥AP,BE⊥AP,

(2分)

又因为DE∩BE=E，所以AP⊥平面BDE,

(4分)

又因为BD⊂平面BDE,

所以PA⊥BD.

(5分)

(Ⅱ)连接AH,设AH∩BD=M，

因为PH⊥平面ABCD，所以PH⊥BD,

(6分)

又因为PA⊥BD，AP∩PH=P,

所以BD⊥平面PAH，

(7分)

即可得AH⊥BD，

(8分)

在Rt△ABD中，AB=2,AD=1,

(9分)

(10分)

(11分)

(12分)

20.解:(Ⅰ)设P(x0,y0)，A1(-a,0),A2(a,0)，

(1分)

(2分)

(3分)

(4分)

(5分)

(6分)

(8分)

(11分)

(12分)

21.解:(Ⅰ)由已知可得f′(x)=ex-ax-1，

(1分)

所以f′(0)=e0-1=0,

(2分)

又f(0)=e0-2=-1，

(3分)

所以切线方程为y=-1.

(4分)

(Ⅱ)由题意可知，若函数f(x)在R上单调递增，

则f′(x)=ex-ax-1≥0恒成立，

(5分)

令g(x)=ex-ax-1，

即证明对任意x∈R，都有g(x)≥0成立.

因为g′(x)=ex-a，

①当a≤0时，g′(x)>0恒成立，

即g(x)在R上单调递增，

又g(0)=0，当x<0时，g(x)

此时不满足条件；

(7分)

②当a>0时，g′(x)>0时，则x>lna；

g′(x)<0时，则x

所以g(x)在(-∞,lna)上单调递减，

在(lna,+∞)上单调递增.

(8分)

若对任意x∈R，都有g(x)≥0成立，

则g(x)min=g(lna)=a-alna-1≥0，

(9分)

(10分)

可知h(x)在(0,1)上单调递增，在(1,+∞)上单调递减，

所以h(x)≤h(1)=0，即g(lna)≤0,

所以当且仅当a=1时，g(x)min=0，

(11分)

综上所述,若函数f(x)在R上单调递增，则实数a的取值集合为{1}．

(12分)

22.解:(Ⅰ)由(x-2)2+y2=3可得x2+y2-4x+1=0，

所以曲线C1的极坐标方程为ρ2-4ρcosθ+1=0.

(2分)

由ρsin2θ=4cosθ可得ρ2sin2θ=4ρcosθ，

所以曲线C2的直角坐标方程为y2=4x.

(4分)

则|OA|+|OB|+|OP|=|ρ1|+|ρ2|+|ρ3|，

(5分)

(6分)

所以ρ1>0,ρ2>0，

(8分)

(9分)

(10分)

23．解:(Ⅰ)当x<-1时，

f(x)=-x-1+(2x+1)+1=x+1，

此时f(x)<0；

(1分)

(2分)

(3分)

(4分)

(Ⅱ)由(Ⅰ)可将不等式2m-|x2-2y+1+a|≥|y2-4x+4+b|化为3≥|y2-4x+4+b|+|x2-2y+1+a|，

(5分)

由题意可知

3≥[|y2-4x+4+b|+|x2-2y+1+a|]min，

(6分)

因为|y2-4x+4+b|+|x2-2y+1+a|

≥|y2-4x+4+b+x2-2y+1+a|

=|(y-1)2+(x-2)2+a+b|

≥|a+b|，

(8分)

所以3≥|a+b|，

(9分)

又因为a+b>0，

所以0

所以a+b的取值范围为(0,3]．

(10分)

(本套联考试题为杂志社第三阶段原创研发项目“数学D3T2”研发组成果)