关于考试大纲删去“几何证明选讲”模块的思考——以解析几何为例

广东

林国红

(作者单位：广东省佛山市乐从中学)

关于考试大纲删去“几何证明选讲”模块的思考
——以解析几何为例

广东

林国红

随着新一轮高考和课程改革的逐步推进，高考数学考试大纲从2017年起作调整，从以前的三个选考模块“极坐标和参数方程”“不等式选讲”和“几何证明选讲”中删去了“几何证明选讲”模块，其余两个选考模块的内容和范围不变，考生从剩下的两个模块中任选一个作答.

高考删去“几何证明选讲”模块是因为这部分内容考查的主要是初中平面几何的知识，而高考中几何的主要知识内容在立体几何和解析几何中均有体现，不需要再单独列为专题考查，删除这部分内容可以减少重复考查，强化学科体系的导向.“几何证明选讲”模块不再单独作为一道试题出现在高考试卷中，但是应该认识到这并不意味着学生不用学习平面几何的知识，也不意味着教师不用再涉及这方面的知识.其实考试大纲删去“几何证明选讲”模块并不是要削弱几何对推理论证能力的考查，在高考试卷中，这部分内容会以更隐蔽的形式“潜伏”在其他试题当中，比如融入到立体几何试题或解析几何试题当中.

下面笔者以几道2017年高考的解析几何题为例，了解平面几何知识与解析几何的融合，并以平面几何的视角结合解析几何的相关知识解决问题，希望可以达到抛砖引玉的效果.

( )

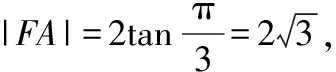
【评注】本题利用抛物线的定义，结合等边三角形的判定及性质等平面几何知识解答，此外还涉及解直角三角形，解题的关键是将已知信息“翻译”成平面几何信息.

【例2】(2017·全国卷Ⅱ理·16)已知F是抛物线C:y2=8x的焦点，M是C上一点，FM的延长线交y轴于点N.若M为FN的中点，则|FN|=________.

【评注】本题利用抛物线的定义，结合相似三角形的判定及性质，减少了运算量.此外本题还可以用平行线分线段成比例定理来解答.

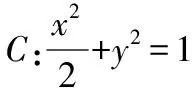
(Ⅰ)求点P的轨迹方程；

【解析】(Ⅰ)略.P的轨迹方程为x2+y2=2.

①+②得(m+n)2+m2-n2=6，即m(m+n)=3.

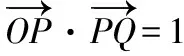
【例4】(2017·全国卷Ⅲ文·20)在直角坐标系xOy中，曲线y=x2+mx-2与x轴交于A，B两点，点C的坐标为(0,1).当m变化时，解答下列问题：

(Ⅰ)能否出现AC⊥BC的情况？说明理由；

(Ⅱ)证明过A，B，C三点的圆在y轴上截得的弦长为定值.

(Ⅱ)设过A,B,C三点的圆与y轴相交于另一个点D(点D在x轴的下方)，根据相交弦定理，得|OC|·|OD|=|OA|·|OB|，即有1·|OD|=-x1x2，所以|OD|=2.因此过A,B,C三点的圆在y轴上截得的弦长为|CD|=|OC|+|OD|=1+2=3，是定值.

【评注】本题中的问题(Ⅱ)用到了圆的相交弦定理，思路巧妙，解法简单快捷，相比于解析法，极大地减少了运算量.

从上面几个例子可以看出，解答解析几何问题时善用平面几何知识，常常可以避开繁难的代数运算，简化解题过程.其中挖掘试题背后有关的几何性质是关键，这需要熟练掌握一些常见平面几何图形的性质，并将其与解析几何的特征量相结合，寻找问题解决的切入点与突破口.因此对于解析几何问题，要将解析法与平面几何法相结合，从而得到解决问题的最优解法.

所以，我们要正确解读高考数学考试大纲中删去“几何证明选讲”内容，这并不意味高考完全回避平面几何的知识，而是将平面几何内容与立体几何或解析几何有机整合，也就是说平面几何知识考得更加隐蔽，更加灵活了.这就要求教师在平时的教学和复习备考当中，要适当加入平面几何知识，并引导学生应用平面几何知识去化解立体几何或解析几何的难度，从而更好地解决问题.

(作者单位：广东省佛山市乐从中学)