高中数学中抛物线的考点和题型总结

四川

谭 莉

(作者单位：四川省成都市新都一中)

高中数学中抛物线的考点和题型总结

四川

谭 莉

根据教学经验，高中数学选择、填空和解答题都比较偏好考查抛物线的相关性质，而且常常作为试卷的较难题甚至压轴题出现，学生拿到这种题，经常算错，或是无从下手，慢慢的，对这种题产生了畏惧心理，因此，对高中数学抛物线的常见考点做一个总结是非常有必要的，如果学生了解了出题人大概会从哪些方面去考查抛物线的性质，就能在平时有意识地加强这些性质的练习，以便熟练掌握和应用，再看到这类题，就不会担心没有思路，也不会担心算不出来了.对于中等生和待优生而言，学生事先知道抛物线考查的方向，打有准备之仗，非常必要.

一、与抛物线相关的常见结论及证明

已知抛物线y2=2px(p>0)，过焦点F作一条直线交抛物线于A,B两点，M为AB的中点，直线l为抛物线的准线，交x轴于E点.P，Q分别为AF，BF的中点.过点A作AA′⊥l于点A′，过点B作BB′⊥l于点B′，过点M作MM′⊥l于点M′.

设A(x1,y1),B(x2,y2)，则有以下结论：

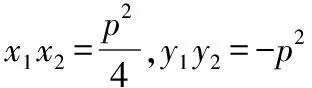
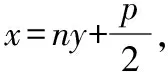
【结论四】以焦半径|AF|或|BF|为直径的圆与y轴相切.

【结论五】以焦点弦|AB|为直径的圆与准线相切.

二、抛物线在选填题中的常考题型

题型一：轨迹方程

【例1】动点M(x,y)到点(2,0)的距离比到y轴的距离大2，则动点M的轨迹方程为________.

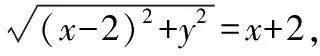
综上，动点M的轨迹方程为y2=8x(x≥0)或y=0(x<0).

【例2】动点M(x,y)到点(2,0)的距离比到直线x=-1的距离大1，则动点M的轨迹方程为________.

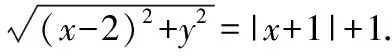
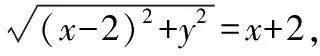
∵y2≥0，∴y2=4(x-1)舍去；

综上，动点M的轨迹方程为y2=8x(x≥0).

以上两个问题考查的是轨迹方程，两个题说法非常相似，仅仅在数据上有所不同，导致结果大相径庭，例1答案由抛物线和射线两部分组成，例2答案只有抛物线这一部分，而学生们经常看到这个题后，会想到抛物线的定义，所以直接找到焦点和准线，算出参数，得到抛物线的方程.这样的做法，会使得例1这种题出现错误，学生得不到分数，所以笔者认为，这两个题应该对比出现，让学生们明白，有时候数据的一点点不同，会造成结果上很大的差异，所以做题的时候，一定要严谨，考虑周全，不能凭感觉解题.

题型二：抛物线的定义

(一)抛物线定义的简单应用

【例3】如图，设抛物线y2=4x的焦点为F，不经过焦点的直线上有三个不同的点A，B，C，其中点A,B在抛物线上，点C在y轴上，则△BCF与△ACF的面积之比是

( )

解析：分别过A,B作y轴的垂线，垂足为A1,B1，

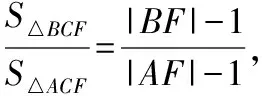
(二)利用抛物线定义求最值的问题

【例4】已知定点Q(2,-1)，F为抛物线y2=4x的焦点，动点P为抛物线上任意一点，当|PQ|+|PF|取最小值时，P点的坐标为________.

解析：过点P，Q分别作抛物线准线的垂线，垂足为P′,Q′，由定义可知，|PF|=|PP′|，

∴|PQ|+|PF|=|PQ|+|PP′|≥|QQ′|,

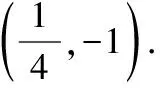
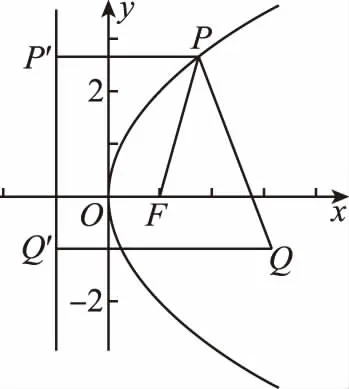
【例5】已知抛物线x2=4y上有一条长为6的动弦AB,则AB的中点到x轴的最短距离为________.

以上三个题，都直接考查了抛物线的定义，在高中阶段，抛物线的定义非常重要，是高考的重中之重，一定要让学生高度重视，例3直接考查抛物线的定义，例4和例5考查的是利用抛物线的定义解决最值问题，比例3的难度大一些，但是仔细归纳一下，也能发现解题的规律，基本上考查的都是两点间直线段最短，或者点到直线的距离最短，所以可以多从这些方面去想，便能找到解决方法.

题型三：以抛物线的焦半径为直径的圆与y轴一定相切

【例6】设抛物线C:y2=2px(p>0)的焦点为F，点M在抛物线上，|MF|=5，若以MF为直径的圆过点(0,2)，则抛物线C:y2=2px(p>0)的方程为________.

本题考查了以焦半径为直径的圆与y轴的关系，不难发现，两者是相切的关系，如果这个题，事先不知道这个性质，学生采用硬算的方式，那么计算量非常大，当然也能得到正确答案，但是在考试的时候，不是每个学生都有时间和能力把这道题硬算出来，如果事先学生知道这个性质的话，哪怕是有一点印象，就会朝着这个方面去论证，然后解决这个题就非常方便了.所以，笔者认为，非常有必要把抛物线的常用性质归纳给学生，让学生们事先有心理预期，这样在考场上才能自信而高效地去攻克这些题.

题型四：抛物线焦点弦的两端点的横坐标之积为定值，纵坐标之积为定值

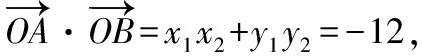
【例8】斜率为k(k>0)的直线l经过点F(1,0)交抛物线y2=4x于A，B两点，若△AOF的面积是△BOF面积的2倍，k的值为________.

【例9】如图，抛物线y2=4x的一条弦AB经过焦点F，取线段OB的中点D，延长OA至点C，使得|OA|=|AC|，过点D,C作y轴的垂线，垂足分别为E，G，则|EG|的最小值为________.

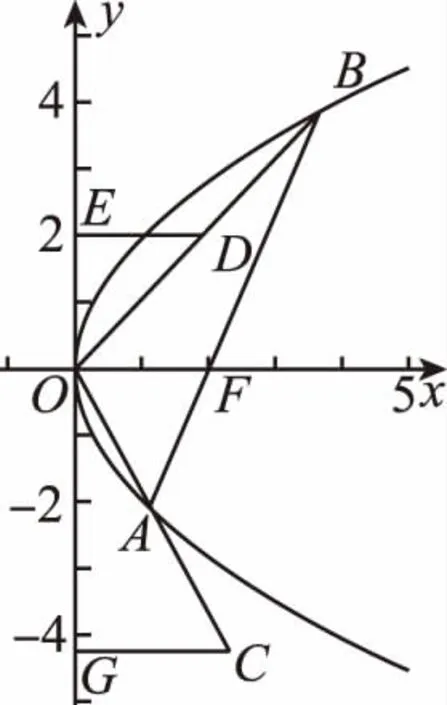
解析：设A(xA,yA)，B(xB,yB)，

由于A，B是焦点弦的两端点，∴yAyB=-p2=-4，

题型五：抛物线的焦点弦被分成的两条焦半径的倒数和为

【例10】斜率为k(k>0)的直线l经过点F(1,0)交抛物线y2=4x于A，B两点，若△AOF的面积是△BOF面积的2倍，则k的值为________.

解析：∵AM，BN都是焦点弦，

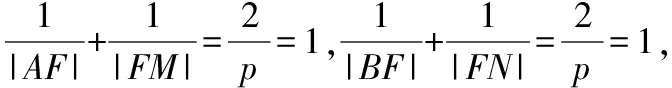
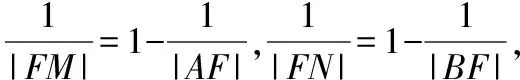
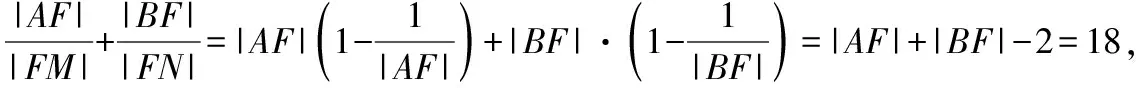
∴|AF|+|BF|=20，

由韦达定理得y1+y2=4n，

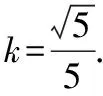
以上两个题，都可以应用同一条焦点弦的两个焦半径的倒数和为定值来解决，例10属于简单题，它和例8是同一个题，有多种解题方法，但是例11属于难题，这个题如果不应用这个性质，硬算是算不出结果的，学生容易选择放弃，但是如果学生知道抛物线的这个性质，并且通过题目，发现此题应该是和焦半径的倒数相关的题，由此对题目中的等式进行化简，即可得到|AF|+|BF|=20，再应用焦半径的公式，可得|AF|+|BF|=x1+1+x2+1=x1+x2+2=n(y1+y2)，联立方程组，利用韦达定理，即可得到答案.

题型六：与抛物线的切线有关的问题

由图可知，当AP与抛物线相切时，∠APB最大，cos∠APB最小.

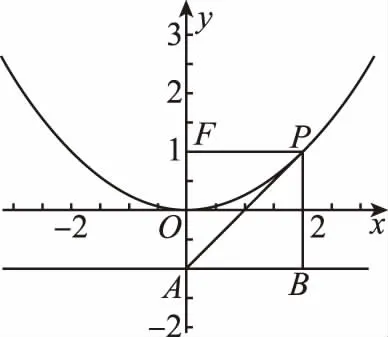
此题也是一个常考题，求m的最值，转化成了求角的三角函数的最值，对应的刚好是直线和抛物线相切的时候，联立方程组，令Δ=0即可，知道这个思路之后，其实做起来很顺利，但是如果不知道思路，这道题往往在选择题8题以后出现，学生在心理上就认为这道题比较难.但是如果已经对这种类型的题的考点有预期的话，其实学生们就只需要静下心来，把一个个环节操作出来即可，所以笔者认为提前给学生们归纳一下考题类型，其实是为了稳定学生心理，让学生们心中有数，心态稳定.

题型七：抛物线的焦半径

【例13】已知P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4)是抛物线C:y2=8x上的点，F是抛物线C的焦点，若|P1F|+|P2F|+|P3F|+|P4F|=20，则x1+x2+x3+x4=________.

解析：由题意，抛物线C的准线为x=-2，由抛物线定义知|P1F|=x1-(-2)=x1+2，

|P2F|=x2+2，|P3F|=x3+2，|P4F|=x4+2.

∵|P1F|+|P2F|+|P3F|+|P4F|=20，

∴x1+2+x2+2+x3+2+x4+2=20，

∴x1+x2+x3+x4=12.

此题是一道容易题，考的是焦半径公式，直接用定义把焦半径换成坐标，即可得到答案，但是如果不从这个方向想，而采用硬算的方式，计算量就会非常大，还不容易求解出来，所以学生们快速筛选出正确简洁的方法至关重要.

题型八：抛物线的参数方程

【例14】过抛物线C:y2=2px(p>0)，作两个相互垂直的弦OA，OB，弦AB的中点M的轨迹方程为________.

∵A，B不是原点，∴t1≠0,t2≠0，

∵OA⊥OB，∴kOA·kOB=-1,

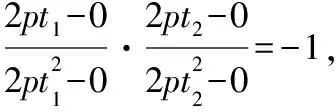
∵M为AB的中点，

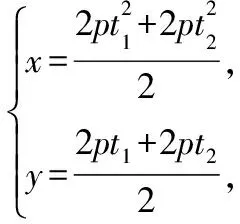
∴M的轨迹方程为y2=px-2p2.

此题如果采用常规方法来求解的话，会比较复杂，但是如果采用抛物线的参数方程把点设出来，把求解的目标表示出来，再采用消参的方式就能顺利求解.而抛物线的参数方程，本质就是引入一个参数t，一个坐标表示成t的一次方，另一个坐标表示成t的二次方，再用点进行计算，或者表示求解目标，最后算出参数的值或者消掉参数，题目不好求解的时候，抛物线的参数方程往往是一种很好的选择.

题型九：联立方程组，利用韦达定理来解决问题

得k2x2-(4k2+8)x+4k2=0，

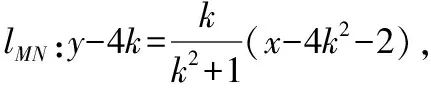
∴直线MN与x轴的交点坐标为(-2,0).

此题是圆锥曲线部分的典型题型，就是直线和圆锥曲线相交于两点，联立方程组，利用韦达定理是解决问题的基本方法，直接进行相应的运算即可，学生对此进行过很多训练，所以不再赘述这种方法.

三、归纳和总结

(作者单位：四川省成都市新都一中)