高考全国卷《三角函数与解三角形》命题规律分析与展望

陕西

韩红军

(作者单位：陕西省宝鸡市麟游县中学)

高考全国卷《三角函数与解三角形》命题规律分析与展望

陕西

韩红军

一、新课标近三年《三角函数与解三角形》高考试题考点统计

1．新课标近三年《三角函数与解三角形》高考理科试题考点统计

年份卷型题型题号分值知识点2015Ⅰ卷选择25三角函数的诱导公式、和(差)角公式选择85余弦函数的图象与性质填空165正弦定理、余弦定理的应用Ⅱ卷解答1712正弦定理、余弦定理、三角形的面积公式2016Ⅰ卷选择125三角函数的性质解答1712正弦定理、余弦定理、两角和的正弦公式Ⅱ卷选择75正弦函数的图象变换、图象对称轴的求法选择95三角函数的诱导公式及二倍角公式填空135两角和的正弦公式、正弦定理等Ⅲ卷选择55倍角公式选择85正弦定理、余弦定理、三角恒等变换、解三角形填空145三角恒等变换、三角函数图象的平移2017Ⅰ卷选择95三角函数图象的变换解答1712正弦定理、余弦定理、和角公式等Ⅱ卷填空145同角三角函数的基本关系式、余弦函数的性质等解答1712三角恒等变换、余弦定理等Ⅲ卷选择65余弦函数的图象与性质解答1712余弦定理、解三角形

2．新课标近三年《三角函数与解三角形》高考文科试题考点统计

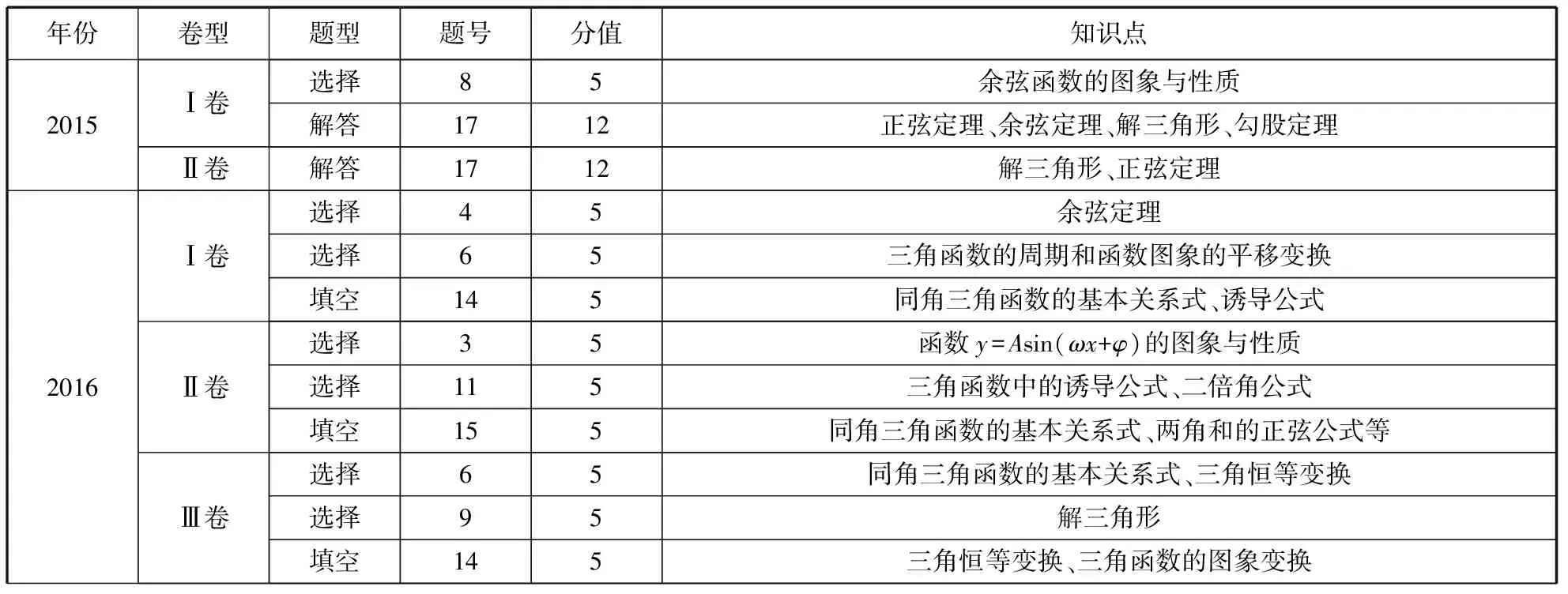
年份卷型题型题号分值知识点2015Ⅰ卷选择85余弦函数的图象与性质解答1712正弦定理、余弦定理、解三角形、勾股定理Ⅱ卷解答1712解三角形、正弦定理2016Ⅰ卷选择45余弦定理选择65三角函数的周期和函数图象的平移变换填空145同角三角函数的基本关系式、诱导公式Ⅱ卷选择35函数y=Asin(ωx+φ)的图象与性质选择115三角函数中的诱导公式、二倍角公式填空155同角三角函数的基本关系式、两角和的正弦公式等Ⅲ卷选择65同角三角函数的基本关系式、三角恒等变换选择95解三角形填空145三角恒等变换、三角函数的图象变换

续表

二、全国高考《三角函数与解三角形》试题分布特点与命题规律分析

考点分类201520162017Ⅰ卷Ⅱ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷合计三角恒等变换与求值第2题第9题第5题第17题3年4考三角函数的图象与性质第8题第12题第7题第14题第9题第14题第6题3年7考解三角形第16题第17题第17题第13题第8题第17题第17题第17题3年8考

从近三年的高考三角试题分布特点与命题规律可以看出，三角试题每年都考，而且文理有别，或“一大一小”，或“三小”，或“二小”(“小”指选择题或填空题，“大”指解答题)，解答题以简单题或中档题为主，选择题或填空题比较灵活，有简单题，有中档题，也有对学生能力和素养要求较高的题.

三角函数的图象与性质是高考考查的重点及热点内容，主要从以下两个方面进行考查：(1)三角函数的图象，主要涉及图象变换问题以及由图象确定函数解析式问题，主要以选择、填空题形式考查，有时也会出大题；(2)三角函数的性质，通常是给出函数解析式，先进行三角变换，将其转化为y=Asin(ωx+φ)的形式再研究其性质(如求ω和φ、单调性、值域、周期性、对称性等)，或知道某三角函数的图象或性质求其解析式，再研究其他性质，既有直接考查的客观题，也有综合考查的主观题.

三角恒等变换主要体现在公式的变形上，包括三角函数的性质，尤其在解答题中更为明显.

解三角形问题是高考的必考内容，主要考查：(1)边和角的计算；(2)三角形形状的判断；(3)面积的计算；(4)有关的范围问题.由于此内容知识交汇性和应用性较强，与其他知识综合、与实际问题结合起来进行命题将是今后高考的关注点.

三、全国高考《三角函数与解三角形》试题命题方向展望

1.三角函数的定义与基本概念

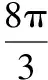
(2)已知角α终边上一点P的坐标是(2sin2,-2cos2)，则sinα=

( )

A．sin2 B．-sin2 C．cos2 D．-cos2

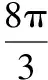
【评注】已知角α的某三角函数值，可求角α终边上一点P的坐标中的参数值，可根据定义中的两个量列方程求参数值；已知角α的终边所在的直线方程或角α的大小，根据三角函数的定义可求角α终边上某特定点的坐标.

2.三角函数式的化简与求值

(1)求cos(α-β)的值；(2)求α+β大小．

【评注】三角恒等变换“四大策略”：(1)常值代换：特别是“1”的代换，1=sin2θ+cos2θ=tan45°等；(2)项的拆分与角的配凑：如α=(α-β)+β=(α+β)-β等；(3)降次与升次：正用二倍角公式升次，逆用二倍角公式降次；(4)弦、切互化：一般是切化弦．

3.三角函数的图象与性质

( )

( )

A.9 B.8

C.7 D.6

( )

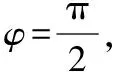
【评注】函数f(x)=Asin(ωx+φ)+B的确定方法：

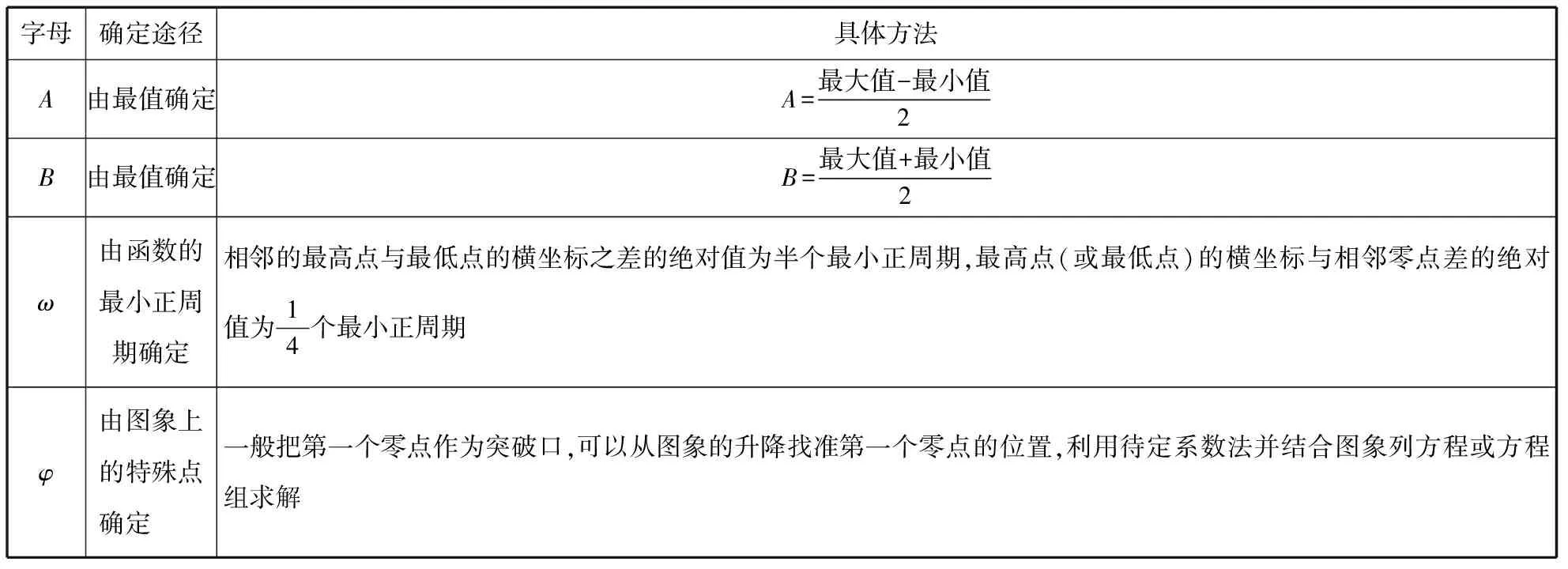
字母确定途径具体方法A由最值确定A=最大值-最小值2B由最值确定B=最大值+最小值2ω由函数的最小正周期确定相邻的最高点与最低点的横坐标之差的绝对值为半个最小正周期,最高点(或最低点)的横坐标与相邻零点差的绝对值为14个最小正周期φ由图象上的特殊点确定 一般把第一个零点作为突破口,可以从图象的升降找准第一个零点的位置,利用待定系数法并结合图象列方程或方程组求解

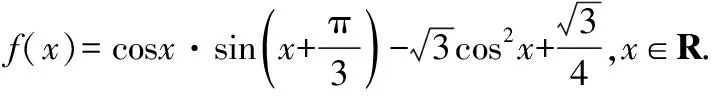
(1)求f(x)的最小正周期；

(2)求f(x)的单调递增区间；

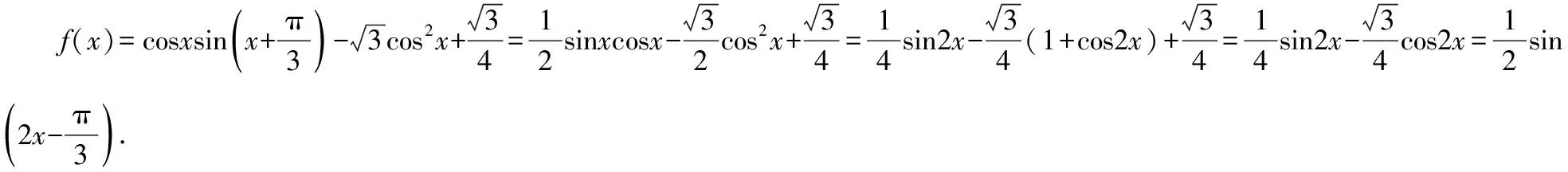
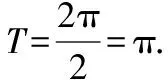
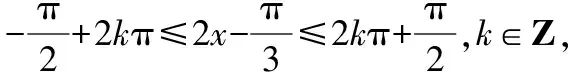
【评注】解决三角函数图象与性质综合问题的方法：先将y=f(x)化为y=asinwx+bcoswx+B的形式，然后用辅助角公式化为y=Asin(ωx+φ)+B的形式，再借助y=Asin(ωx+φ)的性质(如周期性、对称性、单调性及最值等)解决相关问题，因此，要熟悉y=sinx或y=cosx的各种性质.

4.正、余弦定理及其应用

【例5】在锐角△ABC中，角A,B,C所对的边分别为a,b,c，且2bcosC=2a-c．

(1)求角B；

(2)求sinAsinC的取值范围．

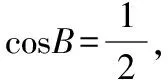
5.解三角形的实际应用问题

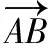
(2)海中有一处景点P(设点P在xOy平面内，PQ⊥OM，且PQ=6 km)，游轮无法靠近．求游轮在水上旅游线AB航行时离景点P最近的点C的坐标．

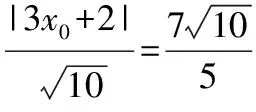
(2)解法一：由题知PC⊥AB时，游轮离P点最近.由(1)知直线AB的方程为x+y-6=0，因为P(4,8)，则直线PC的方程为x-y+4=0，所以解联立直线AB和直线PC得到的方程组，得点C的坐标为(1,5)．

【评注】求解解三角形的实际应用问题时，先要分析题意，分清已知与所求，再根据题意正确画出示意图，这是最关键、最重要的一步．将实际问题转化为可用数学方法解决的问题后，选定或确定要创建的三角形，若其他量已知则直接求解；若有未知量，则把未知量放在另一确定三角形中求解．注意正、余弦定理的“联袂”使用，确定用正弦定理还是余弦定理，如果都可用，就选择更便于计算的定理.一般分为三种题型：(1)求距离；(2)测高度；(3)测角度.

6.三角函数与其他知识交汇

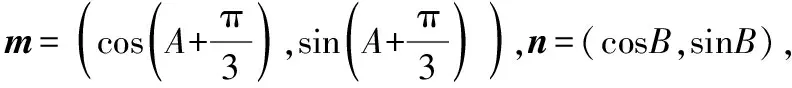
(1)求A-B的值；

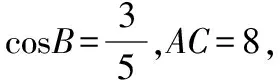
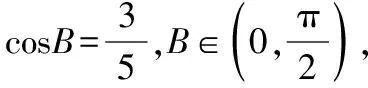
【例8】(2016·黑龙江省牡丹江市)已知f(x)=ax+sinx(a∈R).

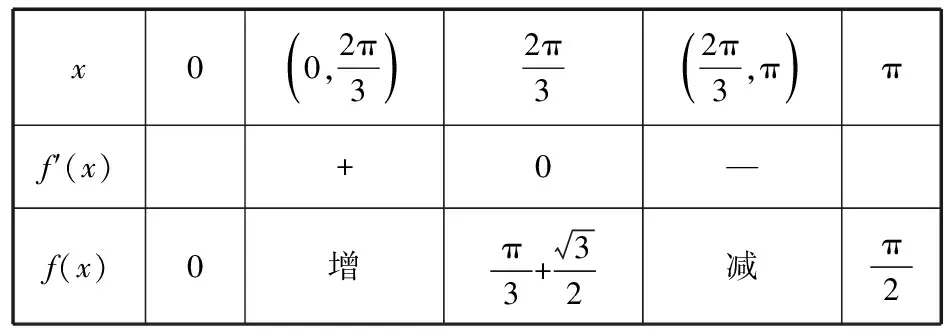
x00,2π3()2π32π3,π()πf′(x)+0—f(x)0增π3+32减π2

(作者单位：陕西省宝鸡市麟游县中学)