平面几何视角下解析几何问题的简解

湖北 李红春

解析几何是一门用代数方法研究几何问题的学科，在高中阶段具有重要的地位，高考中解析几何试题有着较大的区分度，面对繁琐的计算不少学生望而生畏，其实不少解析几何问题如果能有效利用平面几何性质，多一点想，就能少一点算，达到事半功倍的目的．

1.利用解三角形的知识

由三角形中已知边和角求其余的边和角的过程，称为解三角形．解三角形通常需要包含一条边在内的三个已知条件，求解过程中通常需要运用正弦定理和余弦定理．

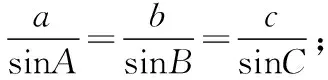
余弦定理：在△ABC中，A,B,C所对的边分别为a,b,c，则a2=b2+c2-2bc·cosA，b2=c2+a2-2ac·cosB，c2=a2+b2-2ab·cosC．

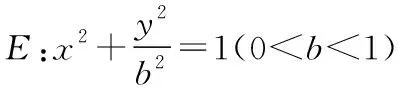
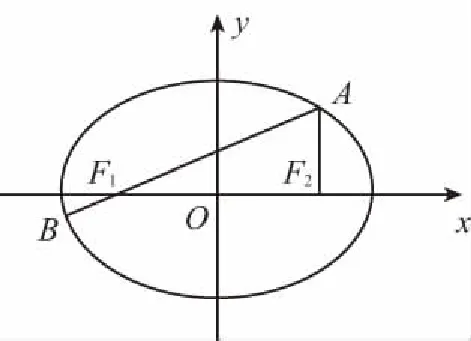
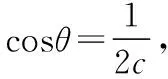
点评：从图形直观出发，借助椭圆定义，运用余弦定理和直角三角形边角关系，回避了直线方程代入椭圆方程的繁琐，简洁至极．

穿孔问题在深水钻孔桩施工过程中较为常见，其主要是指桩基钻进工作进行中，钢护筒内部泥浆以较快速度流失，孔内的水位高度出现了明显的下降，严重情况下会下降到正常水面之下的现象。经过对11#-1钻孔桩出现穿孔问题的原因进行了认真地分析，主要是由于11#-1钻孔桩钢护筒在埋设工作中，存在着明显的倾斜问题，钢护筒底部的偏位情况较为明显，护筒的半径无法满足实际需求。钻孔工作过程中，钻头和钢护筒的底脚部位摩擦较为明显，导致钢护筒埋设深度范围内的砂层稳定性减弱，进而导致穿孔问题的出现[1]。

2.利用三角形相似

如果两个三角形的形状相同，则称两个三角形相似．如果两个三角形三条边对应成比例，或者有两个角对应相等，则两个三角形相似；对于直角三角形而言，如果有一个锐角对应相等，或者斜边和一条直角边对应成比例，则这两个直角三角形相似．

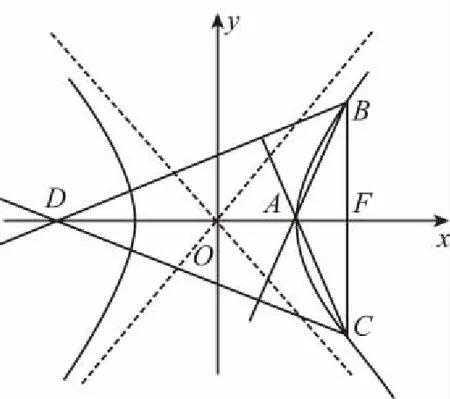
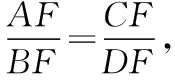
点评：由A是△BCD的垂心，结合图形，容易发现图形中的线线垂直关系，进而挖掘出三角形相似，得到对应边成比例，极大地缩短了思维流程．

3.利用相交弦定理

相交弦定理：如果AB,CD为圆O的两条相交弦，交点为M，则AM·MB=CM·MD．

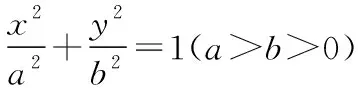
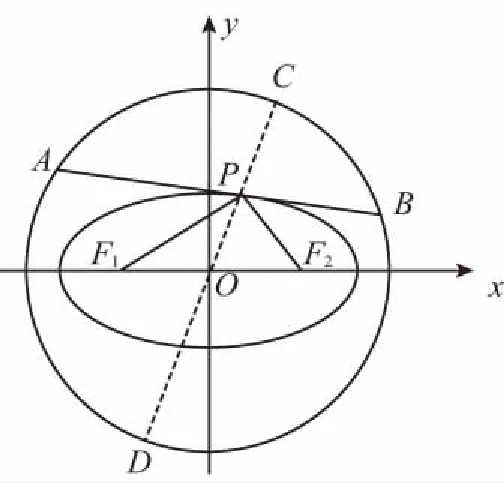
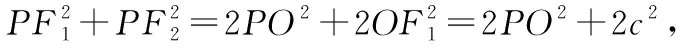
点评：先过点P作出直径CD，再依据中线长定理和椭圆的定义，借助相交弦定理搭起由PA·PB通向PF1·PF2的桥梁，避免了传统解析几何方法计算的繁琐，让人拍案叫好．

4.利用外角平分线的性质

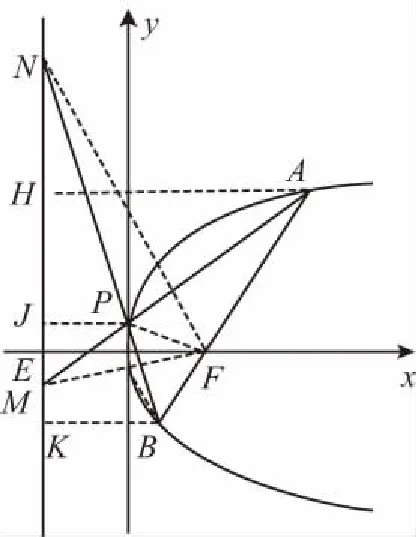
【例4】AB是抛物线y2=2px(p>0)过焦点F的弦，点P是抛物线上异于A,B的任意一点，直线PA,PB分别交抛物线准线l于M,N，则点M,N的纵坐标之积为定值-p2．

证明：作AH,PJ,BK垂直准线于点H,J,K,

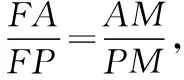
点评：从抛物线定义出发，建立比例关系，借助外角平分线的性质巧妙解题，妙不可言．

5.利用四点共圆定理

四点共圆定理：对角互补的四边形四个顶点共圆．

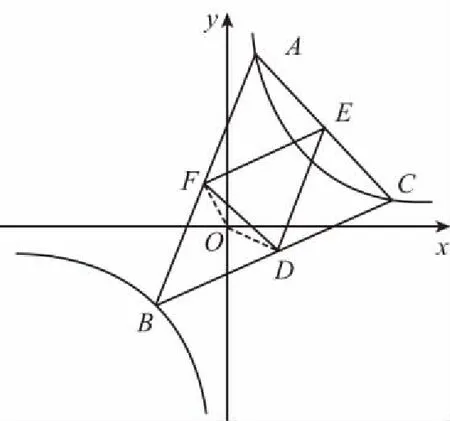
点评：依据对角互补的四边形四个顶点共圆，寻求证明对角互补是破解本题的关键点．

6.利用切割线定理

切割线定理：点A为圆O外一点，AM为圆O的切线，M为切点，AC为圆O的割线，交圆于B,C两点，则AM2=AB·AC．

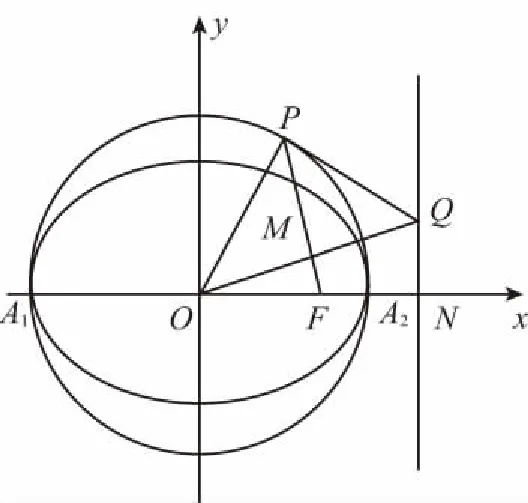
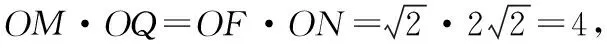
点评：先借助切割线定理，建立等积式，进而得出两三角形相似，再借助相似三角形性质解题，思路清晰，计算量小．

从以上几例不难发现，平面几何注重直观，偏向于“形”，解析几何依赖计算，侧重于“数”，若能将“形”与“数”有机结合起来，充分考虑所给问题的几何属性，善于从图形的几何关系中抓住几何本质，挖掘其几何内涵，并进行适当的运用，便能有效减少解析几何计算量、缩短思维流程，优化解题过程．