关于高中物理习题中关联加速度的一些讨论

安徽 高 鑫

在求解轻绳、轻杆两端关联速度时，常利用沿着轻绳、轻杆方向速度相等的关系来建立方程。在一些问题中也利用到类似的方法，如被轻绳连接的两物体的加速度大小也是相等的，也据此列方程求解。仔细回想不难发现，后者必定是两物体的合加速度就是沿着轻绳方向的，而不需要进行类似速度那样进行分解的，这些题目编写时为什么不约而同的刻意避开分解加速度的问题呢？笔者将结合物理竞赛教学，揭开其中的谜底。

一、加速度沿绳、杆的分量的关系

物体相关速度的特征可分为三类：

1.杆或绳约束物系各点速度的相关特征：在同一时刻必具有沿杆、绳方向的相同的分速度。

2.接触物系接触点速度的相关特征：沿接触面法向的分速度必定相同，沿接触面切向的分速度在无相对滑动时相同。

3.线状相交物系交叉点的速度：相交双方沿对方切向运动分速度的矢量和。

高中阶段要求熟练掌握应用的是第一种，先通过例题来说明关联速度在高中课程中的求解方法。

【例题1】如图1所示，一汽车用轻绳经定滑轮拉船靠岸，不计滑轮大小和质量，滑轮距水面的高度h，若绳与水面夹角为θ时，车向左的速度为v0，加速度为a0(均未必是常量)，试求此时船的速度v和加速度a。

图1 图2 图3

1．船的速度求解

【方法一】速度分解法：

如图2有v平行=vcosθ=v0

【方法二】微元法：

如图3，作图得AC=AD，因∠CAD非常小，故可认为CD垂直于AB，则在△BCD中有BD=BCcosθ，即

2.加速度的求解

对比两解发现，正解比错解多了一项，接下来讨论该项的意义：

小船加速度沿绳方向的分量为a平行=acosθ

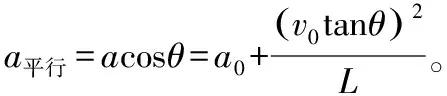
3.多出项的含义

图4

由前面的计算可知，v船对绳=v绳对地tanθ

所以船相对绳末端的向心加速度等于

可见，轻绳、轻杆在非平动的运动中，两端点的速度沿绳、杆方向的分量是相等的，而两端点的加速度沿绳、杆的分量是不相等的，两者之差为一个端点相对于另一个端点的向心加速度。

4.举例应用说明

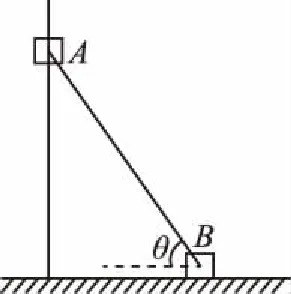
图5

【例题2】如图5所示，物块A穿过光滑的竖直杆，物块B放在水平地面上，两物块通过铰链和轻杆连接起来，轻杆长度为L，如图轻杆和水平面的夹角为θ，物块A正在下滑，速度和加速度分别是v0和a0，求此时刻物块B的速度和加速分别是多少？

【分析】速度关系如图6所示、A、B两物体沿着轻杆的速度分别是

vA平行=v0sinθ，vB平行=vcosθ

可得B的速度为v=v0tanθ

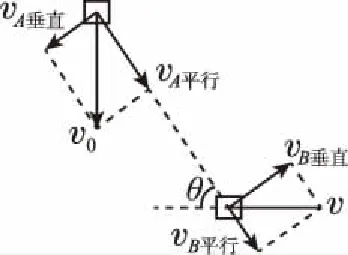
图6 图7

加速度的分解如图7所示，可得到两物体沿着轻杆方向的加速度分别是aA平行=a0sinθ，aB平行=acosθ

图8

平行于轻杆方向的加速度的相互关系是

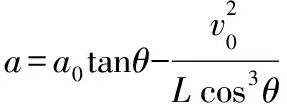
可见不能错误地类比速度的计算方法，错误地得到B的加速度a=a0tanθ。

二、高考范围内的关联加速度关系

在高中阶段，有很多的练习题中都是两个物体的加速度是相等的，接下来用刚才的讨论来进行说明。

1．典型例题

图9

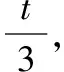
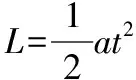
由于m1和m2的速度都是沿着轻绳方向，速度必然相等。又因为m2的速度一直沿轻绳竖直向下，所以相对于轻绳滑轮处没有发生转动，不存在由相对转动而引起的向心加速度。

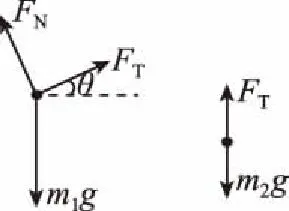
图10

因此m1和m2沿着轻绳方向的加速度也是相等的，m1和m2的实际加速度就是沿着轻绳方向，所以m1和m2的加速度是相等的，第一次都是a，第二次都是a′。

第一次m2g-FT=m2a，FT-m1gsinθ=m1a，得

2．小结