正确创设物理图景 优化高考解题

浙江 厉 杰

建立物理模型的情景式教学是以生动形象的教学情景激发学生的学习情绪与学习兴趣的教学方法。在课堂教学中，教学情景是直观与抽象、感性与理性、教材与生活的桥梁，利用教学情景能化解形象与抽象、新知与旧知、感性与理想之间的矛盾，充分调动学生的学习积极性，培养学生的自主学习能力、分析与解决问题的能力，实现教与学的和谐统一。因而，教师应根据学生的心理和年龄特点创设不同的教学情境模型，激发学生的学习兴趣，诱发学生的情感共鸣，提高课堂教学的有效性。自新课程改革以来，建立物理模型的情景式教学被广泛应用于高中物理教学之中，为物理课堂教学增添了许多新亮点，并收到了良好的教学效果。

物理概念和规律具有抽象性和客观性，而物理习题由于是描述一些理想物体的基本运动或基本状态，所以具有理想性、具体性和形象性。为了沟通概念规律与习题的联系，解题中就应创设具有这种联系的“图景”，通过物理图景，可以使物理过程变得更为形象和清晰，这对于启发学生思维、正确理解物理概念及分析物理问题可以起到良好的辅助作用，同时也可以增加学生的研究兴趣，提升物理水平，从而做到将复杂问题简单化、抽象问题形象化。

一、物理解题时建立情景模型的必要性

1.物理模型是培养学生学习兴趣的重要手段。而情景模型具有真实、直观、便于分解解题步骤的特点，非常容易勾起学生的探索欲望。同时，情景模型又是物理现象、物理过程经过抽象思维处理后在人脑中的产物。通过一个简单的图示，几根线段展现出一个或多个物理过程，以直观和富有规律的情景图像呈现在学生面前，它结合了抽象思维，既富有启发性，又富有哲理性，更容易激发学生的研究兴趣，也更容易解决物理问题。

2.有助于培养学生探究与应用知识的能力。物理模型教学是将新课程理念应用于物理教学的突破口，它改变了传统的填鸭式教学，从具体情景出发引导学生观察物理现象、操作物理实验、认知物理规律，有助于培养学生的自主探究能力、社会实践能力。因而，可以通过物理实验、生活场景、多媒体技术等创设物理情景，在物理情景中引导学生探究物理现象的成因、思考现象背后的物理规律，这样可以培养学生思考和分析问题的能力。从认知心理学来分析，大量的习题巩固，简单的机械作业，往往会使学生“疲于奔命”，逐步散失思考能力，对思维培养是极为不利的，长此以往，也会造成学生审题错误、漏看信息等大量低级错误。如果使用模型教学去创设物理情景，让学生从不同的角度探索解决问题的途径，就会再次点燃学生思维的火花，使学生再接再厉地完成训练，建立模型，体验成功的喜悦，从而培养学生思维的灵活性和发散性。

二、如何有效发挥模型创设在物理教学中的“洪荒之力”

建立正确的模型是情景教学的基础，没有正确的模型只会误导学生，浪费大量的时间精力去求解一个错误的答案。

图形是物理解题中最常用、也是最简单的模型建立方法。用简单的数学图形和线段勾勒出一幅物理情景，将抽象的文字信息融入直观的图形中，可以让学生在短时间内提取更多的有效信息，提高解题效率。图形在人们的视觉认知中起到了非常重要的作用，这从新版物理教材和物理习题中也可见一斑，同时，各地高考试卷中也是多数考题都配有图象或图表，可见图示在物理学习和考试中占据着非常重要的位置。

解决一个物理问题，我们大致可以把思维过程分为两步。首先是审题明确研究对象，定性分析阶段，提取题干中的有用信息，从所给的物理过程、物理情景中建立问题的物理模型、物理图象，然后是定量分析过程，即利用物理学知识求解问题。从这里可以看出来，没有很好的形象思维训练，平时没有养成画图示习惯的同学，无法在第一阶段建立正确的物理情景，也就无法快速、准确地解决物理问题。

以下是一道学生错误率极高的竞赛题，借此来体验一下正确创设物理情景的重要性。

【题目】四个半径为R、质量相等的光滑小球放在一个表面光滑的半球形碗底内，四小球球心在同一水平面内，用另一个完全相同的小球置于四个小球之上，为使下面四小球相互接触不分离，碗半径应满足什么条件？

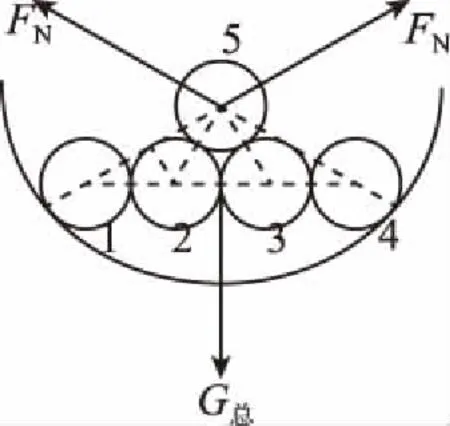
图1

对于模型而言，图1并不是一个好的模型建设方法，所以建立正确的模型是解题的前提。

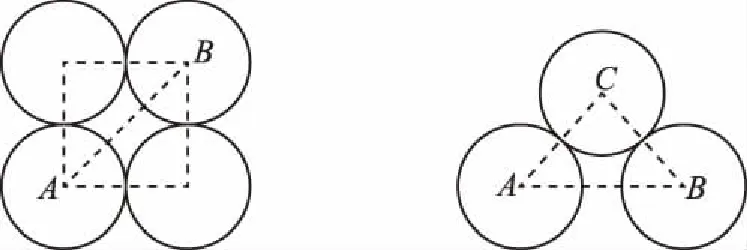
图2 图3

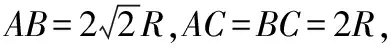
NEA2=(NCAcos45°)2+(G+NCAsin45°)2

又因图5中表示三力的矢量所组成的三角形与图4中△DCA相似，有:

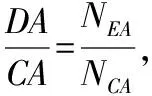
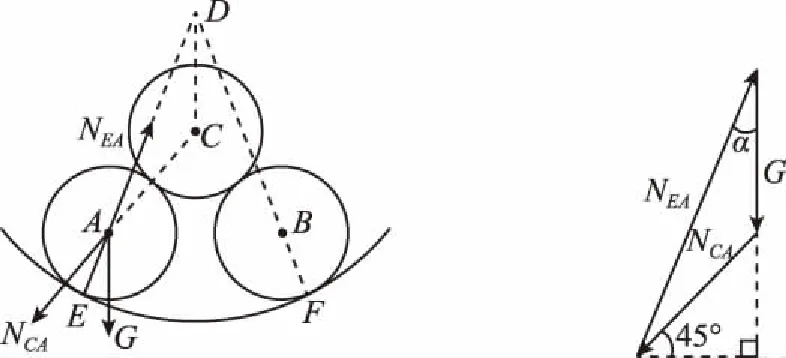
图4 图5

以上解得的r1为系统临界平衡时对应的碗面半径。当r1增大时，图4中碗面对A球的支持力的作用点E将向右移，A所受重力与弹力的合力对E点的力矩不为零，使A球向左转动，四球将分开，原平衡破坏；反之，当碗面半径r1减小时，碗面对A球支持力的作用点将向左移，A球将要向右转动，下面四球之间会出现的弹力阻止上述转动发生，原平衡得以维持。

但是，当碗口半径太小时，其上无法放上四球而平衡，对应于能使四球在碗口上面平衡的碗口最小半径的情况，应为碗口边缘刚好能支于E、F两点，即此时EF两点间的距离为碗口的直径。则碗口半径:

物理过程是指“研究对象”发生物理变化的历程，这个过程可能是持续性的，也可能是短暂性的，我们就是要分析其中规律，帮助学生创设物理模型。在物理图景中所体现的是：通过对实际过程的想象和模拟，所出现的连续、动态的变化过程。应该说，正确分析物理过程是建立清晰、正确物理图景的关键。

在物理模型创设中，我们也可以借鉴数学的解题方法，如数学高次方程的解题方法是三次化二次、二次化一次这样逐一降级的拆解过程。其实建立物理模型解题也是一样，就是把难的问题向已经学过的知识简化，用已知的简单模型去描述抽象的物理情景，一个中等难度的物理题目可以由多个物理情景构成，每一个情景完整地表述一个问题，可以应用独立的方程或方程组。