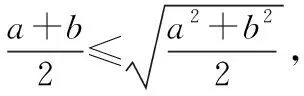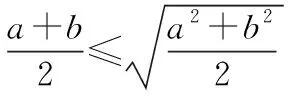利用基本不等式求最值有讲究

江苏 陈伟斌 张启兆

基本不等式反映了两个正数和与积之间的不等关系，所以在求积的最值、和的最值时，基本不等式焕发出强大的生命力，它是解决最值问题的强有力工具，但是利用基本不等式求最值有讲究．

一、理解基本不等式的本质

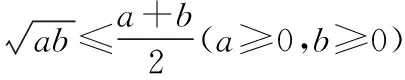
二、牢记三个题根

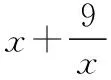
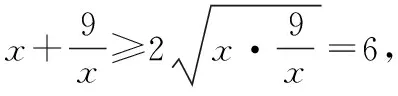
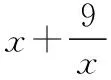
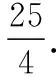
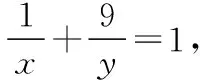
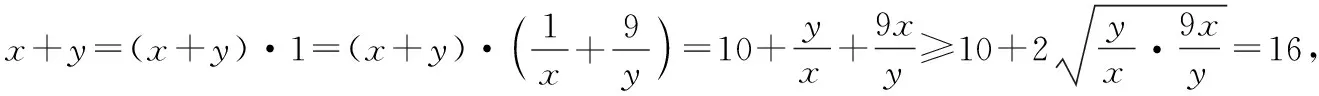
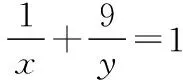
所以x>1．

当且仅当x=4，y=12时，x+y取得最小值16．

评注：属“知和求和”型，使用“常值代换”.

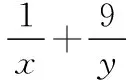
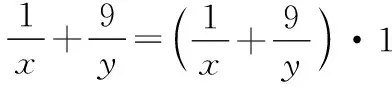
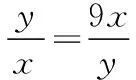
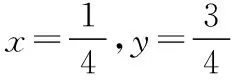
评注：属“知和求和”型，使用“常值代换”.

三、掌握四个策略

1.乘1变换

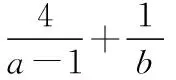
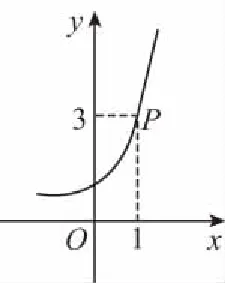
解析：因为函数y=ax+b(b>0)的图象经过点P(1,3)，所以a+b=3，且a>1，所以(a-1)+b=2，且a-1>0，

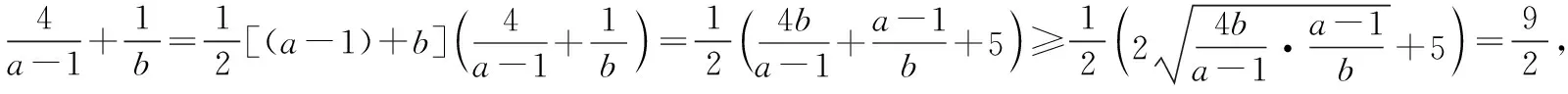
评注：在求和的最小值时，为了凑出积的定值，有时需要乘上1的等价式．本题也可以通过“1的代换”的方法解决．

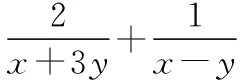
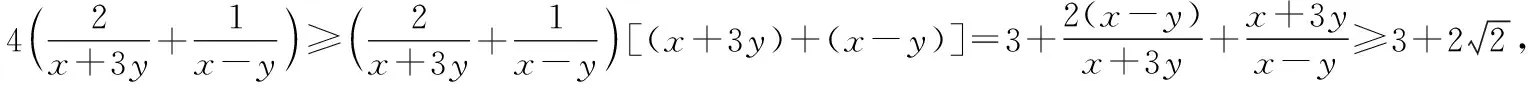
评注：二元函数的最值问题，通常有两个途径，一是通过消元，转化为一元函数，用单调性或基本不等式求解；二是直接用基本不等式，因已知条件中既有和的形式，又有积的形式，不能一步到位求出最值，考虑用基本不等式放缩后求解．

2.1的代换

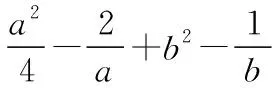
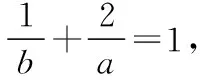
评注：“1的代换”是解决问题的关键，代换变形后能使用基本不等式是代换的前提，不能盲目变形．

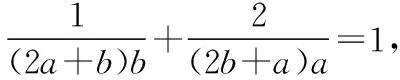
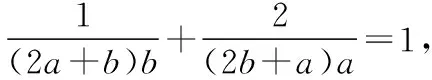
评注：本题已知条件是“和的形式”，目标是“积的形式”，从而联想到基本不等式，采用“1的代换”，把目标转化为一次齐次分式，再用作比换元，问题得以解决．

首先要学会“结构分析”，其次要熟悉不同结构的变形策略，这是处理问题的关键，要思考如何变形才能简化式子，进而达到“和”或“积”为定值的效果．

3.换元法

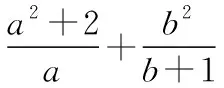
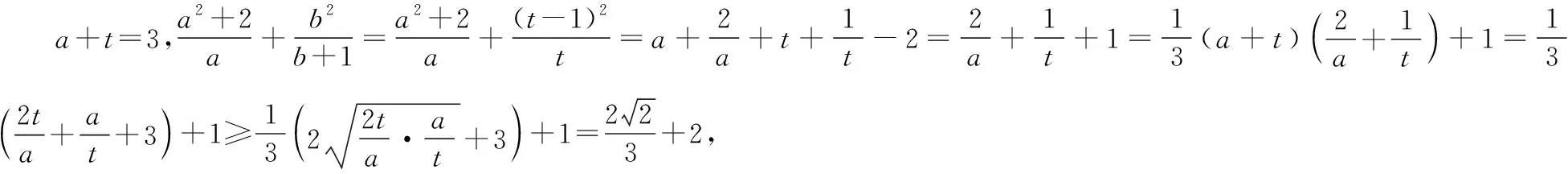
评注：条件不等式的最值问题，通过条件转化成能利用基本不等式的形式求解．换元法是一种常用转化方法，换元法后能使用基本不等式是换元的前提．

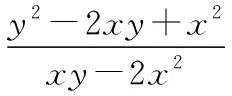
解析：因为正实数x，y满足y>2x，

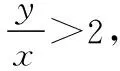
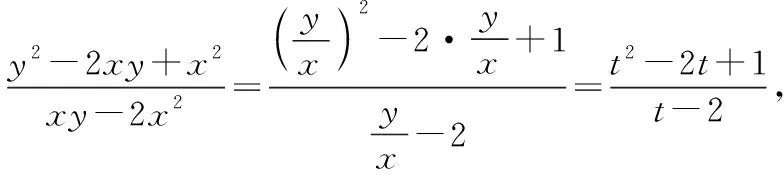
设u=t-2(u>0)，

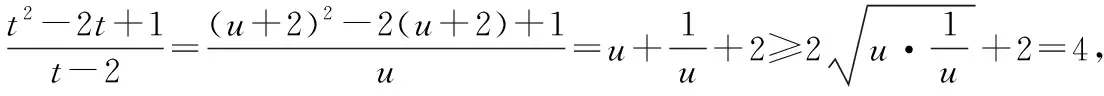
当且仅当u=1，即t=3时取“=”．

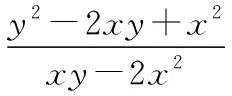
评注：对于二次齐次分式(以本题为例)，分子和分母各项可以同除以x2，也可以同除以xy，还可以同除以y2，再利用换元法，均可以转化为一元分式，从而为基本不等式创造出可应用的情境，这是处理齐次分式的常用手段．

4.利用不等式链

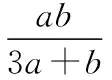
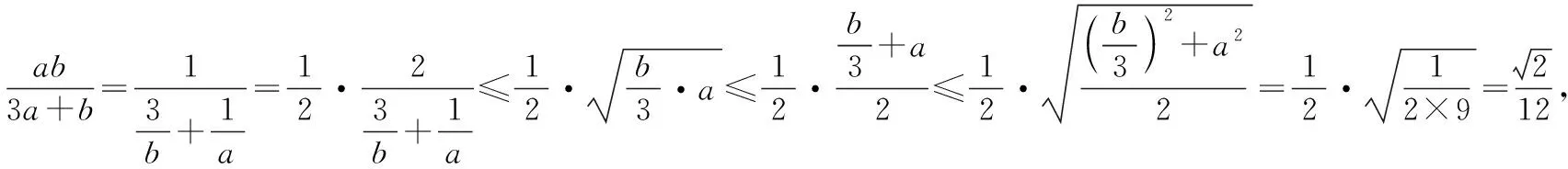
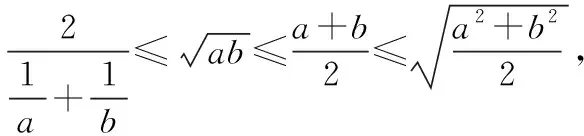
(2)此题直接平方后，可利用二次函数求解．

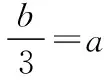
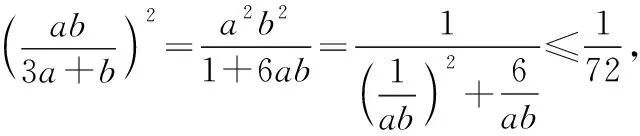
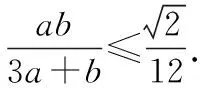
【变式】若a>0,b>0，且a+b=1，则a2+b2的最小值是______ ．