地坑式架车机稳健优化设计

程 兵，于兰峰，符 康，吴永明

（西南交通大学 机械工程学院，四川 成都 610031）

1 引言

地坑式架车机作为动车组三级修程中必备的大型关键设备之一，主要用于举升动车组，更换转向架和对底部进行维修[1]。作为大型检修设备，地坑式架车机整体结构非常复杂，整个16编组地坑式架车机总重达1000t[2]。当前，国内厂家对架车机结构件的设计主要以经验为主，且没有统一的设计规范，校核计算主要参考《起重机设计规范》。为了安全起见，结构强度等性能参数所留余量较大，因此有必要对各结构件进行优化。

然而，国内外在工程实际中，一般采用传统的确定性优化方法，没有考虑一些不确定因素对产品的影响，因此优化结果往往具有较低的可靠性和鲁棒性，进而影响产品质量，产品的可靠性与使用寿命也会大大降低。而地坑式架车机对制造精度和可靠性要求很高，传统优化设计方法已不能满足实际需要。

为解决上述问题，必须对架车机进行稳健优化设计。稳健性设计的概念最早是由Taguchi于1993年提出的，近年来，国外学者对稳健性优化做过不少研究，文献[3]采用正交阵列和复合噪声因素方法，提出了汽车硬质内饰的稳健设计方法，有效提高了车内成员的碰撞安全性。文献[4]将稳健优化方法应用于汽车前车声结构的轻量化设计中。文献[5]结合多目标遗传算法与6σ实验设计，以理论测试函数和实际焊接梁为例，提出了基于6σ的多目标稳健优化设计方法。在总结前人方法的基础上，将近似模型技术、蒙特卡洛模拟法、可靠性分析和6σ质量设计相结合，对地坑式架车机进行稳健性优化设计。优化流程，如图1所示。

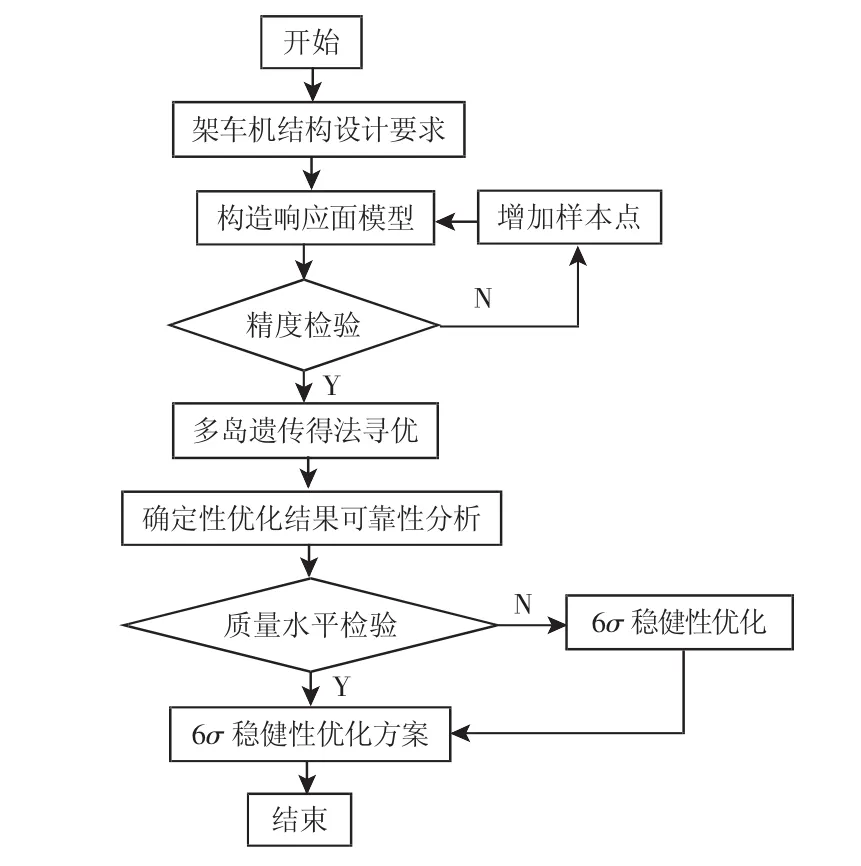
图1 稳健优化流程图Fig.1 Flow-Process Diagram of Robust Optimization

2 6σ稳健优化设计理论

2.1 稳健优化原理

稳健优化设计主要是通过减少和控制目标函数响应的波动，降低在设计点上的敏感性，使目标函数响应均方差减小，达到“均值达到目标”和“均方差最小化”两个目的[6]。确定性优化和稳健优化的关系对比，如图2所示。在不考虑不确定因素对结果的影响时，目标函数在1点处取最小值，此时得到确定性优化解。当随机变量发生±Δx的波动时，导致目标函数发生较大的波动Δf1。而在稳健设计点2，当随机变量发生±Δx的波动时，目标函数的波动Δf2大大减小。因此相比确定性优化解，稳健性优化解虽然目标函数值有所增大，但其可靠性和稳健性大大提高。

图2 稳健优化原理图Fig.2 Diagram of Robust Optimization

2.2 6σ稳健优化设计

6σ稳健优化是以寻找设计空间的“平坦”区域为目标，在满足质量约束要求的可靠性概率情况下，使不确定输入变量造成的输出响应波动最小化。6σ稳健优化设计是一种将可靠性设计、稳健设计和6σ质量管理相结合的新型设计方法，它要求产品质量在均值6σ范围波动时均满足设计要求，从而大大提高产品的可靠性和质量水平。

6σ稳健优化设计相比于传统确定性优化设计不仅优化了设计目标，并且能降低约束条件和目标函数对设计变量变化的灵敏度，大大提高系统稳健性[7]。传统确定性优化问题的数学模型为：

式中：F（x）和Gi（x）—目标函数和约束函数；i—约束函数个数；xu、xl—设计变量的上、下限。

稳健性优化问题的数学模型为：

式中：μx、μy—设计变量和函数响应的均值；σx、σy—设计变量和函数响应的标准差；n—σ的水平数，当n=6时即为6σ稳健优化设计。

3 地坑式架车机稳健优化

以某研究所研制的地坑式架车机为例，地坑式架车机结构简图，如图3所示。该架车机最大举升高度为2.7m，额定举升重量Q=1.7×105N，根据文献[8]，考虑偏载等情况，取载荷放大系数ψ=1.4，故架车机举升结构计算载荷为F=1.4×1.7×105N=2.38×105N。各部件材料均为Q345，材料许用应力为［σ］=275MPa，弹性模量Ex=2.1×1011N/m2，泊松比 μ=0.3，材料密度 ρ=7850kg/m3。对螺母支撑箱丝杠孔处施加对称约束和Y方向平动约束，对导向箱螺栓孔及轨道轮处施加固定约束，并对托头顶部施加竖直方向的载荷和水平方向的摩擦力，重力加速度取9.8m/s2，利用ANSYS建立的架车机结构有限元模型，如图4所示。其中，托头、滑块、滑轨等构件以及较厚板采用SOLID45单元模拟，其余板结构用SHELL63单元模拟，共有64715个节点，54444个单元。

图3 地坑式架车机结构简图Fig.3 Structure Diagram of Underfloor Lifting System

图4 地坑式架车机有限元模型Fig.4 The Finite Element Model of Underfloor Lifting System

3.1 确定性优化

为保证机构各零部件与结构件的连接位置不变，因此只对图3中的立柱、螺母支撑箱及导向箱等主要结构件的板厚进行优化。其设计变量，如表1所示。

表1 架车机各结构件设计变量Tab.1 Design Variables of Various Structural Parts of Lifting System

以地坑式架车机结构自重为优化设计目标，建立以下优化模型：

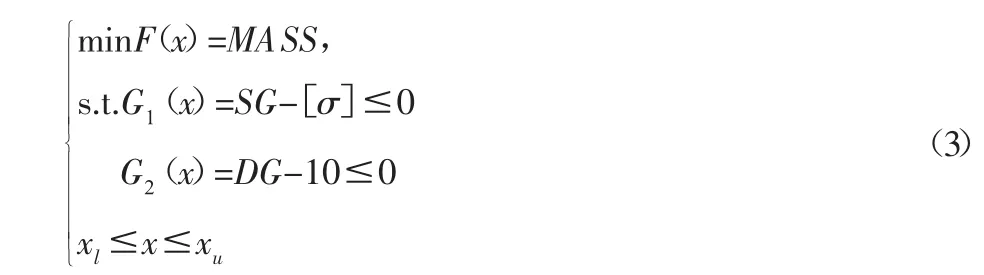
式中：SG—架车机在工作状态下的最大等效应力；DG—架车机在工作状态下最大垂直静挠度，根据设计要求，其最大值不超过 10mm；xu、xl—设计变量上、下限。

利用响应面法构造地坑式架车机的近似模型。近似模型技术是利用数学模型的方法逼近一组输入变量（独立变量）与输出变量（响应变量）的方法[9]。通过近似模型方法，能极大地提高优化算法的寻优速度。由于响应面法能利用较少的试验获得比较精确的逼近函数关系，计算简单，并且拥有很好的鲁棒性，将采用多学科优化软件ISIGHT来构造地坑式架车机的响应面近似模型。为了验证响应面近似模型的可信度，需要对近似模型进行误差分析。通过随机选取150个模型样本点，20个误差分析样本点，对建立的响应面模型进行误差分析，结果显示SG，DG和MASS的R2误差分别为 0．99995，1，0．99996。在 ISIGHT 内置的误差分析模块中，精度评估指标R2误差越接近1，表明响应面模型越接近真实模型，模型可信度越高，因此该模型精度较高，可以代替仿真程序进行优化设计。传统优化算法经常收敛于局部最优解，导致寻优不彻底，利用多学科优化软件ISIGHT提供的全局优化算法—多岛遗传算法（MIGA）对确定性优化模型进行全局寻优，经过10000次迭代计算，得到一组最优解，如表2所示。

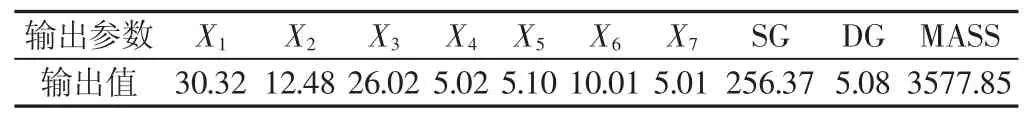
表2 确定性最优解Tab.2 Deterministic Optimal Solution

由表1和表2可以看出，尽管系统的结构自重大大降低，但该优化方案中的X1、X3～X7、SG等参数都非常逼近约束边界。当存在不确定性干扰时，该优化方案极有可能不满足约束条件，从而导致优化方案失效。因此，有必要进行6σ质量分析，对该方案的可靠性与质量水平进行评估，并对模型进行6σ稳健优化。

3.2 6σ稳健优化

在进行6σ优化之前，首先需进行6σ质量分析。其基本思路是对当前设计点进行随机扰动，在其平均值周围生成一组样本点，并通过统计分析估计单一设计点上的输出响应指标的可靠度、σ水平、失效概率和百万缺陷数等，并统计各输出响应指标的均值与标准差[10]。

基于蒙特卡洛抽样的6σ分析是最准确的分析方法，因此采用蒙特卡洛抽样法评估确定性优化方案的质量水平。假设本次优化的设计变量均服从正态分布[11]，采用描述性抽样方法采集样本点，抽样次数设为1000次，获得各响应参数的可靠度和σ水平，如表3所示。由表3可知，除了X2和DG的σ水平和可靠度满足要求外，其他参数的σ水平和可靠度均较低，因此有必要进行6σ稳健优化。

表3 确定性优化与稳健优化对比Tab.3 Comparison of Deterministic Optimization and Robust Optimization

为提高各参数的σ水平和可靠度，在确定性优化的基础上，通过多学科优化软件ISIGHT和有限元分析软件ANSYS集成对模型进行6σ稳健优化。依然采用确定性优化的近似模型，同时，各约束条件和受力情况不变，采用Hooke-Jeeves算法进行稳健性优化，优化结果，如表3所示。

对比表3中的确定性优化解和稳健性优化解可知，6σ稳健优化解各设计变量尽管相比确定性优化解有所增大，但与初始值相比大大减小；经圆整后，架车机的最大等效应力相比确定性优化解减小12．37%，架车机的结构自重相比确定性优化解增加4．85%，但比初始方案减小16．79%。同时，相比于确定性优化解，6σ稳健优化解的各项参数的质量水平均达到6σ，可靠度均为1，因此在尽可能降低结构自重的情况下，架车机的稳健性得到了极大的提高。

4 结论

（1）传统的确定性优化方法由于未考虑不确定因素对产品性能的影响，因此优化结果的可靠性和稳健性较低。将响应面近似模型技术、蒙特卡洛抽样法及6σ质量设计相结合对地坑式架车机进行稳健优化。

（2）通过蒙特卡洛法抽样并进行6σ稳健优化，对比6σ稳健优化最优解、确定性优化最优解和初始方案可知，该方法不仅使架车机的结构自重明显降低，还能大幅提高架车机的可靠性和稳健性。为地坑式架车机的结构设计和改进提供参考依据，具有较强的理论与实际意义。