传感器尺寸对高速列车空气动力学测试影响

何洪阳，陈麒天，陈春俊

（1.中国核动力研究设计院，四川 成都 610041；2.成都外国语学校，四川 成都 611731；3.西南交通大学 机械工程学院，四川 成都 610031）

1 引言

随着列车的运行速度不断提高，空气动力效应加剧[1]。列车表面压力分布不同而产生气动载荷，气动载荷直接影响列车的行车安全、能耗、气动噪声、气动振动及车内气压舒适性等[3-4]。因此，对列车表面压力准确测试至关重要，线路试验是研究列车空气动力学最直接的方法。为了减小传感器自身尺寸对测点处流场的影响[4-5]，选取航空航天领域常用的贴片式微型超薄压阻式气压传感器。由于传感器的体积小，通常线路试验时忽略传感器自身尺寸对测点流场影响。然而，传感器自身尺寸对测点流场影响未知，需进一步探究其测试误差，以此来修正测试信号。

针对这一问题，以某CRH型高速列车为研究对象，在头车侧面中部某测点处建立含有传感器的列车模型，在不同典型速度级下采用大涡数值模拟（Large Eddy Simulation，LES）方法数值仿真计算测点处的表面压力，利用希尔伯特-黄变换提取出脉动压力，并与无传感器的单独列车模型相同测点处的表面压力相比较，建立由于传感器自身尺寸带来的测量误差与运行速度之间的函数关系。对线路试验时列车表面压力信号进行修正，为高速列车气动性能分析提供更准确的试验数据。

2 线路试验测点处压力

列车线路试验时，通常将微型压阻式压力传感器贴在车体表面，测试其测点处的压力信号。列车表面压力可分解为平均压力和脉动压力，前者形成平均载荷，后者形成脉动载荷[6]。由于传感器自身尺寸影响，引起平均压力和脉动压力的测量误差，并且测试压力信号易受电磁温度等随机干扰。因此，测点处压力信号可表示为：

式中：P（t）—测点处压力信号；P0（t）—平均压力(t）—脉动压力；ΔP0（t）—传感器自身尺寸带来的平均压力测量误差；Δ（t）—传感器自身尺寸带来的脉动压力测量误差；n（t）—电磁温度等随机干扰。

3 模型建立

3.1 列车简化模型

以某CRH型高速列车为研究对象，头尾车具有相同的形状。为减小CFD的计算量，建立由头车和尾车组成的列车计算模型，头车长10．5m，宽 3．38m，高 3．7m，2节列车的简化模型，如图1所示。

受计算条件及动车组复杂外形的限制，在不影响计算精度的情况下，作如下假设：（1）当列车以＞250km/h速度运行时，以列车宽度为特征长度计算的雷诺数R＞106，流场处于湍流状态，可采用大涡数值模拟和壁面函数模拟车体表面周围的流场；（2）几何模型建立时，认为车体是一个具有光滑外形的几何体，在一定程度上忽略轮轨系统、转向架及悬架系统、门窗凸起部位和受电弓等。

图1 列车简化模型Fig．1 Train Simplified Model

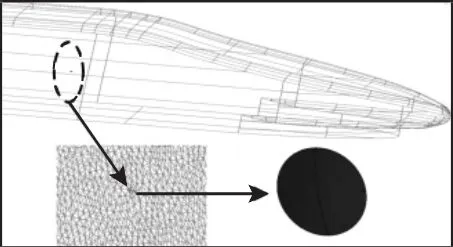
图2 传感器简化模型Fig．2 Sensor Simplified Model

3.2 传感器模型

列车表面压力测试中，贴片式微型超薄压阻式气压传感器因为其体积小、重量轻、灵敏度高等优点，被广泛用于航空器和高速列车表面压力测试。常用传感器尺寸为直径6．35mm，厚度0．76mm的圆片，在动车组车外表面压力实际测试过程中，采用胶带将传感器粘贴于列车表面。因此，考虑胶带粘贴后，传感器测点在列车表面的形状为上底面直径8mm、下底面直径30mm，高1mm的梯形圆柱。压阻式气压传感器的简化模型，如图2所示。

3.3 外流场模型

列车明线交会和通过隧道时，会在车体表面形成复杂的交会压力波和隧道压力波，难于从这些复杂压力波提取脉动压力。因此选取明线运行工况，理论上外流场的计算区域应该无限大，计算结果才能更接近真实值。然而外流场区域越大，其网格质量增加，对计算机内存及性能提出更高要求。

采用滑移网格技术实现车体运动，整个计算区域分为外流场计算区域和滑移网格区域，含有车体的滑移网格区域以车体速度运行，外流场区域保持静止。不同区域间的数据交换通过交界面（interface）进行。在不影响精度的基础上缩小计算区域，将计算区域确定为[7]：列车宽度方向为车宽的10倍左右，高度方向为车高的15倍左右，运行方向上的外流场尺寸要大于列车长度的20倍以上，整个计算区域长、宽、高分别为（323×44×30）m，同时将车体离地面的距离设置为0．2m。

4 数值仿真计算

4.1 网格生成及仿真设置

为了达到大涡数值模拟的精度，同时提高计算机的运算速度，将滑移网格区域分为三部分：起始部分、车体部分及运动方向部分，如图3（a）所示。起始部分（长度取100m）和运动方向部分（长度取250m）的结构简单、尺寸规则，采用六面体结构网格技术，通过控制space ratio参数使靠近车体部分网格进行适当的加密，远离车体部分网格较疏；车体部分由于高速列车模型较为复杂，采用四面体非结构网格，车体表面设置10层网格加密，第一层网格厚度为0．4mm，邻两层边界层网格保持1．5倍的增长比[7]，总厚度为57．7mm；外流场区域采用结构化网格，靠近车体部分的计算区域网格加密，外流场区域网格总数约为540万。最后将滑移网格区域和外流场区域合并在一起，生成湍流流场模拟的整个计算区域，网格总数约为1323万，计算区域网格划分的细节图，如图 3（b）所示。

图3 滑移网格区域及网格划分细节图Fig．3 Sliding Mesh Area and Details of Grids

设置地面及车体表面为无滑移壁面边界（Wall），外流场区域选择压力边界条件（Pressure-outlet），表面压力设置为0Pa，外流场区域与滑移网格区域的交界面设置为Interface。主要仿真计算车体表面压力及提取脉动压力，选择大涡数值模拟为湍流数值模拟方法、Smagorinsky-Lilly模型为亚格子模型，SIMPLE作为求解算法。采样频率 f取 10kHz，取（0．1～0．2）s之间数据进行分析。

4.2 脉动压力提取

选择头车为研究对象，在距离头车8m的车体二位侧表面中心位置建立如2．2节所述的传感器模型，记传感器位置处为测点A。单独列车模型在测点处的表面压力记为P0，含传感器模型的列车模型在测点处压力记为P1。同时在网格划分时，对传感器模型建立一个单独Part，得到传感器模型的上底面网格尺寸在1mm左右，相比于其直径8mm来说，保证传感器模型的网格质量，避免网格质量对计算结果带来的影响。

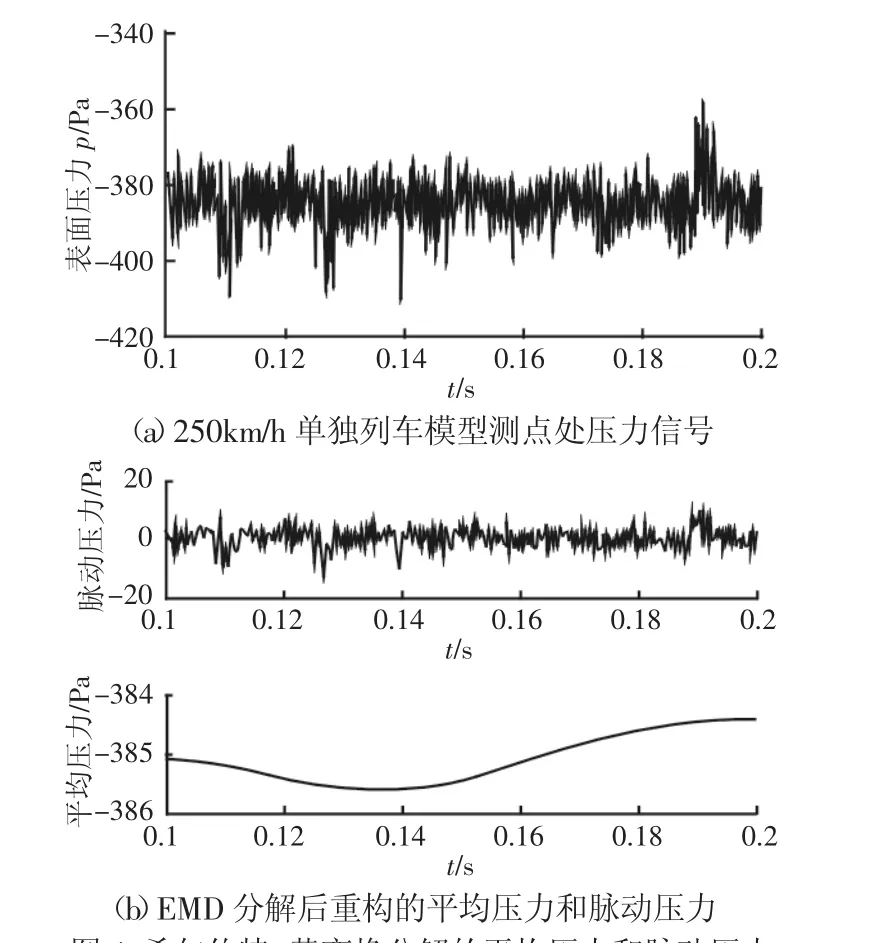
图4 希尔伯特-黄变换分解的平均压力和脉动压力Fig．4 Mean Pressure and Fluctuation Pressure of Hilbert Huang Transform Decomposition

250km/h速度级下，单独列车模型在测点处的表面压力信号，如图4（a）所示。可将P0视为测点处表面压力的真值，可知表面压力信号的幅值约为-380Pa，时域内随机波动±20Pa左右。

希尔伯特-黄变换[8]（Hilbert-Huang Transform，HHT）能将复杂信号自适应地分解成多个单一分量，更深层次反应信号内部特征；常用于研究非平稳、非线性的空气湍流问题[9-10]。运用希尔伯特-黄变换从列车表面压力信号中提取脉动压力。对信号进行EMD分解，自适应分解为9层，分别为IMF1～IMF8分量和余项r；每个IMF分量都有相应的主频，但各个频段的幅值具有很大差异，本征函数的频率从IMF1～IMF8逐渐减小，直到得到残差函数。因此，余项r可视为平均压力，其它IMF分量之和构成脉动压力。EMD分解及重构后的平均压力和脉动压力，如图4（b）所示。平均压力幅值约为（-385）Pa，脉动压力幅值约为（±20）Pa。

5 结果分析

5.1 对平均压力影响

250km/h速度下，对含传感器的列车模型进行仿真计算，取测点处的压力信号P1，并与理论真值P0相比较。由于传感器自身尺寸影响，导致测点处表面压力由（-385）Pa减小到（-425．5）Pa左右，可知传感器自身尺寸对车体表面压力影响极大。同理，采用大涡数值模拟方法计算在300km/h、350km/h速度下单独列车模型和含传感器的列车模型在测点处的表面压力，并求解其测量误差的绝对值ΔP，如表1所示。

用幂函数拟合测量误差绝对值ΔP与运行速度v之间的函数关系为 ΔP=a×vb，其中参数 a=3．697×10-3，b=1．687。可知随列车运行速度v增大，引起的测量误差绝对值ΔP也增大，测量误差绝对值ΔP近似与运行速度v呈二次函数关系。

表1 测量误差绝对值与运行速度关系Tab.1 Relationship Between Absolute Value of Measurement Error and Running Speed

5.2 对脉动压力影响

在250km/h、300km/h和350km/h速度级下，运用希尔伯特-黄变换从车体表面压力信号提取脉动压力信号。脉动压力和声压之间存在着对应关系，根据式（2）求出测点处脉动压力级（PFL），并通过快速傅里叶变换将脉动压力时域转化到频域。各速度级下脉动压力级波动范围及波动幅度，如表2所示。

表2 各速度级下脉动压力级波动范围及波动幅度Tab.2 Wave Range and Amplitude of Fluctuation Pressure Level at Different Speeds

式中：p0—基准压力（为2×10-5Pa）；psf（y，t）—测点计算脉动压力值。

各速度级下脉动压力级具有宽频特性，可用负指函数拟合在整个频段内的变化规律，低频处幅值较大，而高频处幅值较小；由于传感器自身尺寸影响，测点处脉动压力幅值大于真值，如表2所示。同理用幂函数拟合脉动压力级改变幅值ΔPPFL与运行速度 v 的幂函数关系，即 ΔPPFL=1．368×10-7×v2．835，即脉动压力级改变幅值ΔPPFL与运行速度v的三次方近似成正比。

实际工程试验时由于采样频率限制，仅能测量某特定频率段的车体表面压力。在计算脉动压力级的基础上，推导出总脉动压力级L的数学表达式：

式中：Li—频率i处的脉动压力级。

计算各速度级下单独列车模型和含传感器的列车模型在测点处脉动压力的总脉动压力级，如表3所示。可知含传感器的列车模型测点的总脉动压力级比理论真值较大；且随速度增大其总脉动压力级L增大，然而由于传感器自身尺寸引起的总脉动压力级改变幅值ΔL几乎相等。

表3 各速度级下测点处总脉动压力级Tab.3 Total Pressure Fluctuation Level at Different Speeds

6 结论

针对高速列车表面压力测试过程中，传感器自身尺寸会对测点处流场产生影响，导致测试的平均压力和脉动压力结果不准确。建立含传感器模型的列车模型，利用商业软件FLUENT进行大涡数值模拟，利用希尔伯特-黄变换提取脉动压力；并与单独列车模型相同测点处的压力值进行比较，分析传感器自身尺寸带来的测量误差，并建立与运行速度的幂函数关系。得出如下结论：

（1）由于传感器自身尺寸影响，测点处的平均压力绝对值远大于理论真值，且随运行速度增大其绝对误差也增大；且测量误差与运行速度关系为：ΔP=3.697×10-3×v1.687，即近似与运行速度呈二次函数关系；

（2）传感器自身尺寸导致测点处的脉动压力值偏大，脉动压力级改变幅值ΔPPFL与运行速度v的幂函数关系：ΔPPFL=1.368×10-7×v2.835；但各速度级下总脉动压力级改变幅值几乎相等。

传感器自身尺寸会改变测点处湍流流场，导致测试结果不准确。利用上述建立的幂函数关系式可修正测试数据，进而为空气动力学测试及性能分析提供更准确的试验数据。