城市电动物流车EPS系统模糊PID控制策略研究

孟令广，牛志刚

（太原理工大学 机械工程学院，山西 太原 030024）

1 引言

汽车作为人们生活中最常用的交通工具，其数量正不断增加，汽车所消耗的能源和排放的废气也不断增加，这种趋势与当今社会的节能、环保两大主题相背离[1]。因此，许多国家都开始研究新能源汽车。

助力转向系统是现代汽车结构中必不可少的一部分，传统液压助力转向系统存在结构复杂、效率低、易泄露等弊端；而电动助力转向系统只依靠电动机提供转向助力，具有机构简单、控制灵活、效率高等诸多优点[2]。并且助力电机只是在有转向操作时才转动，与液压助力相比可以显著降低能耗[3]；此外，还可以提供合理的助力转矩来适应不同的车速，更好地协调了驾驶轻便性和路感[4]。

控制方式的选择是EPS（ElectricPowerSteering，简称EPS）系统的重要部分，尤其是控制规律的选择[5]。传统的PID控制策略由于在参数设置上的固定性导致助力转向系统对于外界条件改变下的适应能力变差，而且不具有在存在干扰条件下自我调整的功能。模糊控制由于其独特的计算原则，对于没有准确数学模型控制系统具有较强的适应性与自我调整性；模糊PID控制策略在结合上述两种控制方法的基础上，充分发挥了PID控制策略消除稳态误差的特点，又很好地避免了控制对象数学模型不确定情况下产生的参数不固定的情况，发挥了模糊控制的优势[6-7]。在设定好的模糊控制规则的自我调整下，不需要推导出EPS助力转向系统的准确数学模型就可以对非线性的转向系统进行良好的控制[8]。

2 EPS系统的结构及工作原理

电动助力转向系统的组成结构，如图1所示。转向器选择齿轮齿条式，助力方式为转向轴助力式，方向盘转矩通过扭矩传感器来测得。当驾驶员有转向操作时，扭矩传感器发出一个电压信号，电子控制单元（ECU）根据电压信号值计算出方向盘转矩的大小和方向；同时，车速传感器将检测到的当前车速传递到ECU。ECU先根据车速选择与之对应的助力特性曲线，再根据方向盘转矩计算出目标助力转矩的方向和大小，最后确定助力电机的旋转方向和驱动电流的大小，助力电机根据得到的驱动电流提供相应的助力转矩，经减速器减速增扭后施加到转向机构，为转向系统提供与工况相适应的助力[9]。

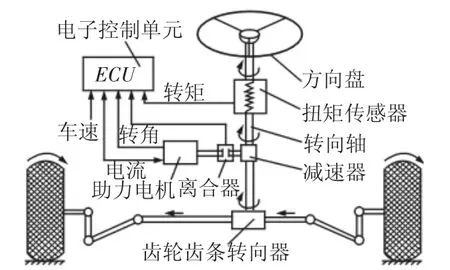
图1 电动助力转向系统机构简图Fig．1 Diagram of EPS

3 助力特性曲线选择

汽车的行驶环境比较复杂，在不同的行驶工况转向时，转向系统根据当前车速选择适合的助力特性曲线，再根据方向盘转矩和选择的助力特性曲线计算出需要提供的助力转矩的大小，从而保证汽车在低速转向行驶时的轻便灵活性和高速转向时的路感。

现如今普遍采用的助力特性曲线有：直线型、折线型和曲线型。这三种曲线中，直线型最简单，数据量小，便于存储，降低了控制系统的设计要求，并且方便调整，适合用在前轴负荷较小的汽车上[4]；曲线型最复杂，能够实现连续均匀地提供助力，但数据存储量大，调整起来比较繁琐，适合用在前轴负荷较大的汽车上；折线型的助力特性介于两者之间。试验中改装的是一款城市物流车，其电子控制技术和智能化水平都不是很高，运行工况相对良好，为了在保证助力需求的基础上尽可能的降低成本，故选用直线型助力特性曲线。

EPS系统在不同车速所对应的助力曲线参数，如图2所示。实验车的最高车速约为100km/h，x轴是驾驶员作用在方向盘上面的力矩，范围在（0～8）N·m，y轴是助力电机作用在转向轴上面的助力转矩，最大为14．8N·m，在车速为0km/h时取得。图中可以看出车速较低时，助力特性曲线的增益系数相对比较大，使低速转向时更加轻便灵活；车速较高时，助力特性曲线的增益系数比较小，保证了高速转向时驾驶员的路感。

图2 理想电动助力转向模型Fig．2 The Ideal Model of Electric Power Steering

4 EPS系统数学模型的建立

建立动力学模型时，为减小仿真模型与真实情况的误差添加相应阻尼、刚度系数等。

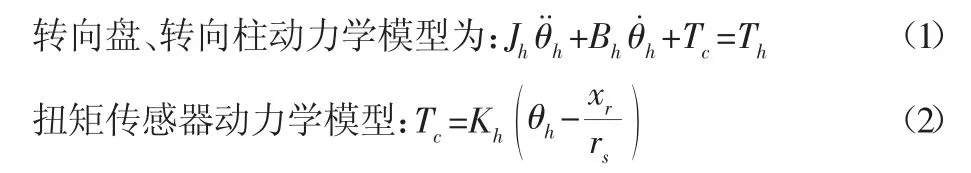
助力电动机动力学模型[10]：

式中：Th、Ta、Tc、Tm—方向盘转矩、电机助力转矩、扭矩测量转矩、助力电机输出转矩；θh、θm—方向盘转角、助力电机转角；Jh、Jm—方向盘和助力电机的转动惯量；Kh、Km、Ka、Kb—转向柱刚度系数、助力电机刚度系数、助力电机电磁转矩系数、助力电机反电动势常数；xr—转向横拉杆位移；rs—转向小齿轮分度圆半径；U、R、L、I—助力电机的电压、电阻、电感、电流；Bh、Bm、Br—转向柱阻尼系数、助力电机阻尼系数、转向横拉杆阻尼系数；G—减速机构传动比；Mr—转向横拉杆质量；FTR—转向负荷。

5 EPS系统模糊PID控制器设计

控制器设置两个输入量和三个输出量，以计算得到的理想电流与实际检测到的电流的误差e和误差变化率ec作为输入，经过模糊PID控制器的运算得到控制系统的精确参数，进而控制电动汽车的助力转向执行器，使汽车转向模型按照理想的助力转向特性进行转向。

以模糊PID作为控制策略的EPS系统流程图，如图3所示。先将精确的输入量电流误差e和误差变化率ec转化为模糊的语言变量E和EC，然后根据模糊规则进行模糊推理得到输出值的语言变量ΔKP、ΔKI和ΔKD，再将语言变量、和解模糊化得到精确的输出值Δkp、Δki和Δkd，实现控制参数的实时控制。

图3 基于模糊PID控制的EPS系统Fig．3 Fuzzy PID Control for EPS System

5.1 模糊语言设计

模糊控制器的语言变量有5个：电流误差e、误差变化率ec和PID三个参数的修正值。其中电流误差e和误差变化率ec为输入变量，Δkp、Δki和Δkd为输出变量。电流误差e和误差变化率ec的基本论域分别为［-15，15］，［-7，7］；在线调整 3 个输出变量Δkp、Δki和 Δkd的基本论域分别为［-2，2］，［-0．6，0．6］，［-0．02，0．02］。变量 e、ec、Δkp、Δki和 Δkd都采用 7个模糊子集描述，即｛NB、NM、NS、ZE、PS、PM、PB｝。

5.2 模糊控制规则

为了实现在线调整PID控制参数的目的，根据不同的电流误差e和误差变化率ec，Δkp、Δki和Δkd的控制规则，如表1～表3所示。

表1 Δkp模糊控制规则表Tab.1 ΔkpFuzzy Control Rule Table

表2 Δki模糊控制规则表Tab.2 ΔkiFuzzy Control Rule Table

表3 Δkd模糊控制规则表Tab.3 ΔkdFuzzy Control Rule Table

6 EPS系统仿真分析

6.1 仿真模型

实验用车在MATLAB/Simulink中搭建的系统模型，如图4所示。汽车EPS系统的整体控制模型，如图4（a）所示。封装的模糊PID控制器运算系统，如图4（b）所示。模糊控制器首先将精确的车速和转矩参数做模糊化运算，再对照模糊规则执行模糊推理，最后对输出结果的模糊变量解模糊化处理，从而得到比例、积分和微分系数的最后调整值Δkp、Δki、Δkd，代入下式计算：

式中：kp0、ki0、kd0—参数设置的初值；kp、ki、kd—最后调整结果。

图4 EPS系统模糊PID控制仿真模型Fig.4 Fuzzy PID Control Simulation Model for EPS System

6.2 仿真结果分析

以阶跃信号为输入，助力转矩为输出，对EPS系统模型进行仿真。不同车速下PID与模糊PID仿真结果对比，如图5所示。

其中，图5（a）为当V=20km/h时，助力特性曲线的增益系数为1.55，如果此时方向盘输入4N/m的转矩，则助力转矩应为6.2 N·m。当系统采用传统PID调节时，调整时间为0.41s，超调量为16%；当采用模糊PID控制策略时，系统调整时间降低为0.2s，超调量为8.8%，模糊PID的控制性能明显优于PID控制。

图5（b）又对车速分别在V=40km/h和V=60km/h时系统的响应特性进行了仿真，车速在V=40km/h时，传统PID调整时间为0.42s，超调量为17.4%；模糊PID控制策略调整时间为0.2s，超调量为8.6%。车速在V=60km/h时，传统PID调整时间为0.41s，超调量为16.9%；模糊PID控制调整时间为0.19s，超调量为8.6%。结果表明采用模糊PID控制策略的EPS系统助力特性具有超调量小、调整时间短的特点，可以很好地满足不同车速的助力转向需要。

图5 不同车速PID与模糊PID仿真结果对比Fig.5 The Contrast of PID and Fuzzy PID Simulation Results in Different Speed

汽车在实际运行过程中，由于路况等因素的改变，会对转向系统产生一定干扰，针对这一现象，在仿真中加入干扰信号验证模糊PID的抗干扰能力，结果，如图6所示。在0.7s时，施加26%的干扰信号，模糊PID在0.12s的调整后重新达到稳定；而PID则需要0.25s的调整时间，由此可见，模糊PID控制策略的抗干扰能力也优于PID。

图6 有干扰时PID与模糊PID仿真结果对比Fig.6 The Contrast of PID and Fuzzy PID Simulation Results with Interference

7 结论

以EPS系统为控制对象，借助模糊PID控制策略解决了被控对象没有精确数学模型的问题，运用Simulink进行仿真，获取了EPS系统的控制参数。（1）在相同输入信号下，模糊PID较传统PID超调量减少，调整时间减少，优化了EPS系统的助力特性。（2）汽车在不同车速转向时，模糊PID均能快速平稳的提供助力转矩，很好地满足转向需求。（3）汽车在许多复杂的工况行驶，采用模糊PID控制策略可使系统对外界的干扰及时进行调整，从而提高EPS系统的抗干扰能力。