促进深度学习，提升数学核心素养

王新甫

【摘 要】随着新课程的实施，广大教师都在关注教学方式和学习方式的变革，呼唤着深度学习的发生，關注着学生数学素养的提升。而综观课堂教学，不难发现，数学教学活动往往浅尝辄止，缺乏一定的思维深度。因此，教学必须打破传统教学中学生被动学习的状况，抓住数学核心内容，围绕数学学科本质，积累数学活动经验和数学思想方法，聚焦思维过程，形成数学素养，发展数学思维，使学生真正触摸深度学习的迷人风景。

【关键词】深度学习；数学素养；思维能力

所谓深度学习是指在教师引领下，学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程。在这个过程中，学生能够掌握学科的核心知识，学会主动思考，逐步提高解决问题、发展批判性思维、创新能力以及学会学习等认知策略，使儿童的思维逐步由易到难、由浅入深，举一反三，从而能够让每个儿童的学习潜能都得到培养与开发。而综观我们的课堂教学，不难发现，数学教学活动往往浅尝辄止，只是简单的学习一些表面的知识，而忽视了让儿童了解这些数学知识中隐藏的逻辑，缺乏一定的思维深度，使儿童的思维始终处在“浅层活动”，这也大大影响了课堂教学效果。深度学习，倡导像呼吸一样自然，注重学生学习的真正发生，直指儿童学习的本质，催生学生学习方式的变革。

一、深度学习意味着什么

数学学习所历练的并不是与人无关的枯燥的符号与规律，而恰恰是引领我们如何探究和发展的意义世界。深度学习，倡导学习像呼吸一样自然，关注儿童学习的自然发生，直接指向学习的本质，让学习真正发生。

（一）联想与结构，深度学习发生的起点

联想与结构既是学生学习方式的样态，又是学生学习时所面对的学习内容。作为学习方式的样态，要经历外在知识转化为内在经验的过程。教学时，教师要通过精心设计，营造适合儿童学习的情境，调动儿童全身心地参与新知识的学习，同时，还要根据知识本身内在的逻辑关系，把需要学习的新知识与已有的旧知识形成结构性关联，使新知识逐步内化为和儿童个体有着关联的并可操作与思考的对象。例如，约分既是分数基本性质的运用，又是进一步对分数基本性质意义的理解。儿童所学习的知识并非是杂乱无章零散的，都是有内在的逻辑和体系的；儿童对新知识的学习，不是盲目地去探究，而是在教师的启发引导下，根据要学习的内容去观察、猜想、验证、推理和联想，充分调动并激活自己已有的知识经验，把所学的新知识逐步内化，以构建新的知识体系。

其实，儿童的知识经验不仅包括结构性知识，还包括非结构性知识经验及背景。儿童的学习方式，不仅仅是简单模仿，或是被动接受成人的思维模式或策略，而要激活自己已有的知识经验去过滤和解释新信息，以达到知识的同化，从而掌握新知识。

（二）活动与体验，深度学习发生的力点

活动与体验是深度学习最为显著的特征之一，数学学习活动是以学生为主体的主动活动，数学学习中的体验是指学生个体在数学活动中全身心投入活动时的内在体验。要让学生真正成为学习的主体，就必须在课堂教学中提供让学生参与活动的机会，从而使他们去亲身经历知识的发现、形成和发展的过程。综观我们的课堂教学，教师往往会忽视学生学习活动的主动性，而直接将知识灌输给学生。当然，学生亲历知识的形成过程，无须像人类最初研究发现知识那样，而是通过教师启发引导，通过自己的探究活动把符号化的知识打开，把静态的知识激活，充分体验感悟知识本身蕴含的丰富复杂的内涵和意义。由此，教学不再是人们所讽刺的枯燥简单的无趣活动，而是情感与理智并在的，鲜活的有温度的学习活动。固然，儿童对知识的理解，不仅包括“结构性知识”，更包括“非结构性经验背景”。儿童的学习，不仅仅靠模仿或接受成人的思维策略或模式，重要的是激发其内在知识经验去过滤和解释新信息，以至知识的同化。因此，与其说儿童是“学习数学”，不如说是儿童经验的“数学化”。

（三）本质与变式，深度学习发生的原点

把握知识本质的过程，就是去除知识非本质属性的干扰，分辨出知识本质与其非本质属性区别的过程，也是对知识内容再次进行深度加工的过程。因此，把握知识的本质就不能简单由教师直接告知，而要通过儿童的主体活动去把握，或者是“质疑”“探究”，或者是“归纳”“演绎”，或者是“情境体验”等，让学生与所学知识内容建立一种紧密的内在联系。只有这样，知识的本质才会显现，要把握知识的本质内涵，学生不仅要具有深刻而灵活的思维特质，还要会对所学内容进行深度加工，从而认识本质的多样性，能举一反三。例如“角的认识”教学，不仅要认识“锐角”，还要认识“直角”“钝角”“平角”“周角”等，只有这样学生才能全面把握“角”的本质含义，避免形成“角是尖尖的”这种片面认识。

（四）迁移与应用，深度学习发生的远点

有学习就会有“迁移”，“应用”是“迁移”的表征之一，也是检验儿童学习结果的最佳方式。应用既是上一个学习环节的结果，又是下一个环节新知识学习的开始。为此，学习内容的结构性、系统性，以及学生学习时的自觉性、主动性和积极性，都会在迁移与应用中得以体现。

“迁移与应用”和“本质与变式”有着内在的必然联系。儿童在学习活动的过程中，先是准确把握知识本质内涵，然后才会有知识的迁移与应用。本质与变式则是突出对知识内容的内化，而迁移与应用则体现对儿童学习结果的外化，它不仅是对学习结果的检验，更是对学习结果的扩展与提升。例如“混合运算” 的教学，许多教师认为混合运算顺序是一种规定，没有什么道理可讲，可采用讲授法直接告诉学生。教学中，笔者设置了日常购物的场景：小红去商店买3个足球和1个篮球，篮球每个55元，足球每个45元，小红要付多少钱给商店呢？学生很快先算“3个45元是135元”，然后再加上55元等于190元。笔者同时引导学生列出综合算式：55+45×3，45×3+55，比较无论45×3在前还是在后，都要先算乘法，后算加法。借助生活中的实际问题，学生很清楚地理解了“先算乘法”的合理性。应用是将内化了的知识外化的过程，也是把间接经验直接化，抽象问题具体化，是儿童学习成果的体现。

二、走向儿童深度学习的教学策略

（一）从“无意”走向“有意”，挖掘数学知识的核心内涵

数学教材是进行课堂教学的依据，也是学生学习数学知识的载体。就数学教学而言，教师先要专心研读教材，剖析所教内容，了解学科本质，挖掘数学知识的核心内涵，从而联系学生实际，精心设计教学预案。从“无意”走向“有意”，学生的学习才有可能是深度的。

例如“乘法分配律”的教学片段。

师：我们已经知道什么是乘法分配律，你能用简单的方法来表示它吗？

生：我用文字表示：（我+爱）×学=我×学+爱×学。

生：我用图形表示：（△+□）×○=△×○+□×○。

生：我可以用字母表示：（a+b）×c=a×c +b×c。

师：比较一下，哪种方法最好？为什么？

生：第三种表示方法好，因为用字母来表示很简洁。

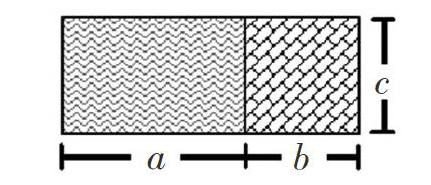
生：我是用图形的面积表示。

出示：

师：你是怎么想的，能说说吗？

生：两个小长方形的面积的和是 a×c +b×c，也就是大长方形的面积：（a+b）×c，也就是（a+b）×c =a×c +b×c，这就是乘法分配律。

对乘法分配律的阐述，教材安排了分三个阶段来认识，先是具体的数的运算，然后是用语言进行描述规律，最后用字母来表示规律。应该说用语言来描述规律是较低层次的表述，用更精练、更简洁的字母表示规律，这是较高层次的表述；而用数形结合的数学思想方法，将乘法分配律与图形进行有机结合，这是更高层次的表述。就乘法分配律的表现形式从单一提升到了多元，学生深刻理解了乘法分配律的核心内涵，提升了思维的品质。

（二 ）从“点状”走向“多维”，建立数学教材的结构体系

数学知识之间是紧密联系的，要使学生有数学眼光，形成问题意识，展开深度学习，教师就要从“点状”走向“多维”，充分重视和强化信息反馈的作用，对教学活动中反馈的各种信息，应及时适度处理，并采取有效的教学对策，从而诱发主体内因，达到帮助学生掌握知识、搭建数学教材结构体系的目的。

例如“数的整除的复习”的教学，就教材而言与整除相关的数学概念达50多个。学生头脑中所呈现的概念表象多是呈线状的知识链，也就是纵向联系的多而横向联系的少。概念的呈现是零碎的、杂乱的且多样的，更是不连贯的。教学时，教师可改变传统的“复习概念—巩固练习—综合练习”的常规复习教学模式，采用认知构建的新型复习教学模式，即“再现知识—→整理知识—→运用知識”。教学时，选择“偶数”这个概念作为知识梳理的起点，让学生去充分表述和“偶数”这个概念相关联的知识，从而对“数的整除”这一单元的所有概念来个“大盘点”， 使得所有数的整除的知识点“横成片”“竖成线”。学生自主复习的兴趣一直处于高涨状态，学生原有单一的线状认知结构逐步被立体的网状认知结构所替代。

（三）从“牵引”走向“生成”，丰富学习过程的体验活动

耗散理论认为，思维临界点被激沸后，会产生新的宏观量级的涨落，并因和外界信息交换而趋于稳定。学生“学”的起点往往又是动态发展新的生成点。当儿童思维平衡被打破后，往往在其独立思考后会萌发大胆创意的设想，课堂教学中随着情智的积累、时间的推移、环境的变化等，学生便在求变求通中从浅层突围，生数学之情，入数学之境。

例如“分数与百分数的互化”的教学，学生在阅读分数化成百分数的结语“把分数化成百分数，通常先把分数化成小数（遇到除不尽时，通常保留三位小数），再化成百分数”时，便提出质疑：“课本中怎么有两个‘通常，是不是重复了？”面对质疑，全班学生都动了起来，讨论着，交流着。最后一致认为：前面的“通常”是针对分数化为小数的方法而言的，后面的“通常”是针对保留几位小数而言的，它们各自有着不同的作用。面对课堂中出现的“异样的质疑”，教师没有回避，而是直面生成，并加以引领，从而巧妙地解决了学生提出的问题，使得课堂教学不仅有知识的广度和深度，更使儿童的思维得以充分彰显。

敏锐地捕捉不期而至的生成点，即时做出判断，应学生而动，应情境而变，使静态的、固定化的教学预设变成丰富的、动态的、富有灵性探究的场景，可使学生思维呈现持续高涨的开放状态，新旧知识间的矛盾冲突可导致学生因疑而思，由思起疑的思维新境界，促成学生高层次思维重组，激活学生主体的深度思维。

（四）从“童趣”走向“创新”，找寻创新思维培养的生长点

与其他学科相比，数学学习是从符号到符号，学习的过程简单枯燥，但数学的“趣”往往来自对数学的思考。在数学学习中，面对学生学习起点的差异性和发展的可能性，教师可以通过与后续学习接轨、与教学同类联姻等方式高筑起点，使儿童的思维与旧知识碰撞重组，并挖掘一切“有趣”因素，巧“疏”妙“导”，打破常规，变换角度，从“童趣”走向“创新”，让个性思维充分站立。

例如“三角形的三边关系”的教学，在学生认识“三角形任意两边之和大于第三边”才能围成三角形的结论后，教师设计了这样一道开放题：“两根小棒，一根是8厘米，一根是6厘米，如果把其中一根小棒剪成两段，能围成一个三角形吗？”

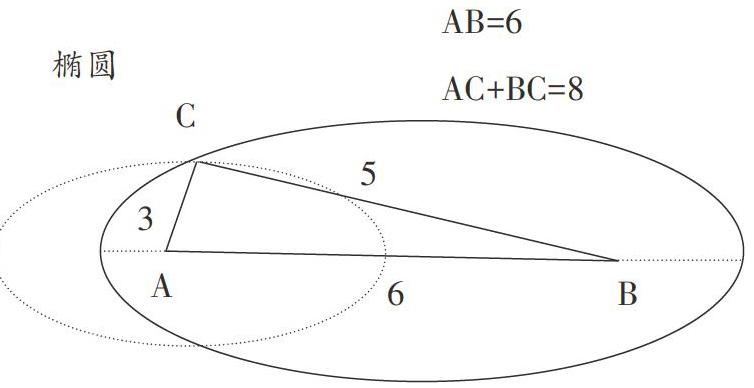
学生通过操作、探究得出“6厘米、6厘米和2厘米”“5厘米、3厘米和6厘米”“4厘米、4厘米和6厘米”可以围成三角形。接着教师又进一步追问“如果把小棒的长度分成是小数，能围成多少种三角形呢？”学生的思维开始弥散，得出3.1和4.9，2.1和5.9，1.1和6.9等无数种。一个又一个开放变化的问题，激活了学生的数学思维。学生在层层探究中，不仅加深对三角形三边关系的理解，而且在潜移默化中受到对应、函数和极限等数学思想方法的浸润。学生的思维走向更远的地方。更有学生在进一步理解三角形三边关系的基础上用图展示了三条边在椭圆内的运行轨迹。

由此，课堂始终处于一种开放的状态，学生各种奇思妙想奔涌而出，创造的闸门一经打开，思维临界点便被激沸。对围成三角形三条边长由整数可能变小数，从数字变图形的多层变式中，儿童的思维逐步走向清晰，其创新能力得以无限接近浑圆式的饱满，在愤启悱发中生成数学课堂别样的精彩。

深度学习是对学生学习一种较高要求，是让学习真正发生的有效途径。作为教师要抓住数学核心内容，围绕数学学科本质，促成学生学会知识，学会思考，积累数学活动经验和数学思想方法，聚焦思维过程，形成数学素养，发展数学思维，使学生真正触摸深度学习的迷人风景。

参考文献：

[1]顾正理. 深度引导：让学生的数学学习思维不再“被搁浅”[J]. 教育探索，2015（12）：41-43.

[2]庞舒勤，赵庆林. 让学生体验深度学习——以小学数学教学为例[J]. 人民教育，2013（22）：38-40.

[3]郭华.深度学习及其意义[J].课程·教材·教法，2016（11）：25-32.

（江苏省宝应县城中小学 225800）