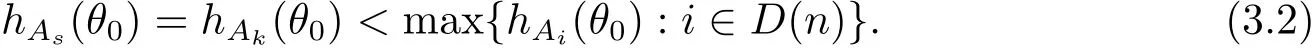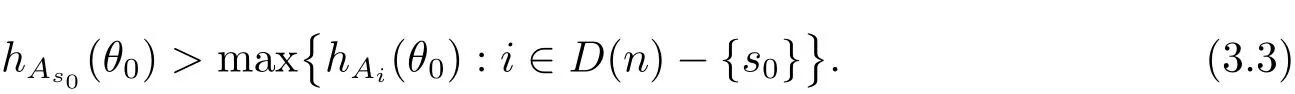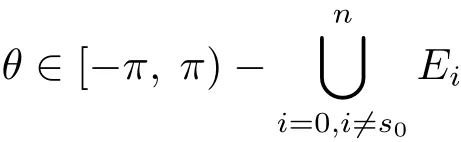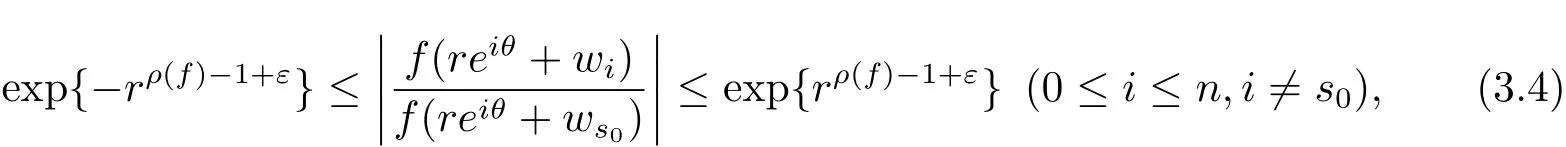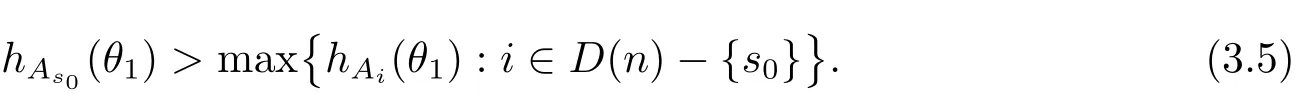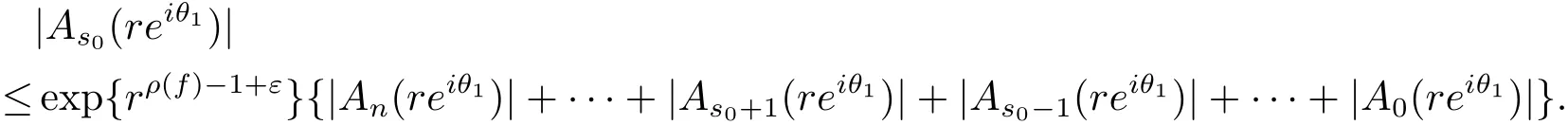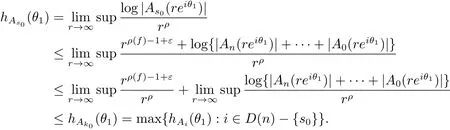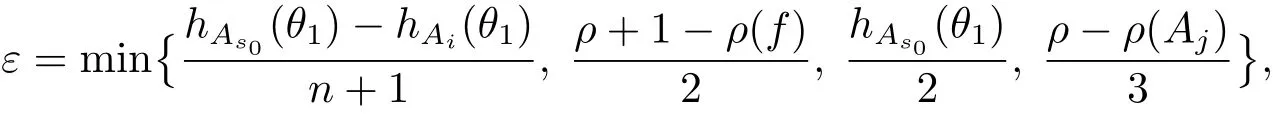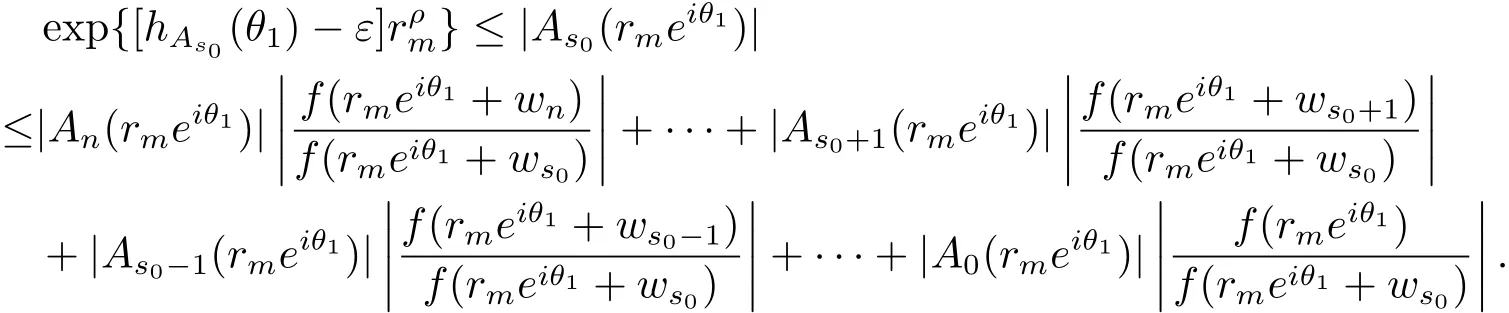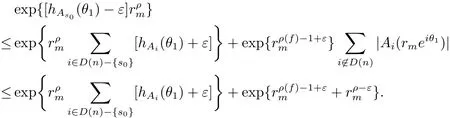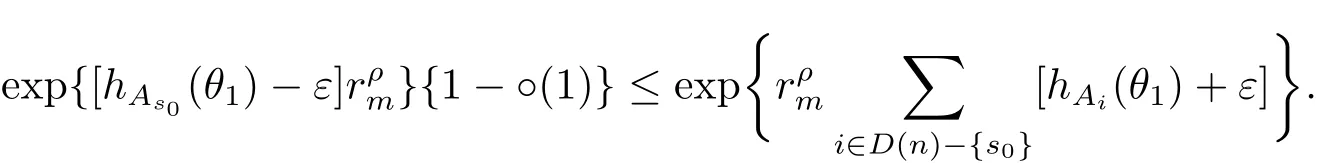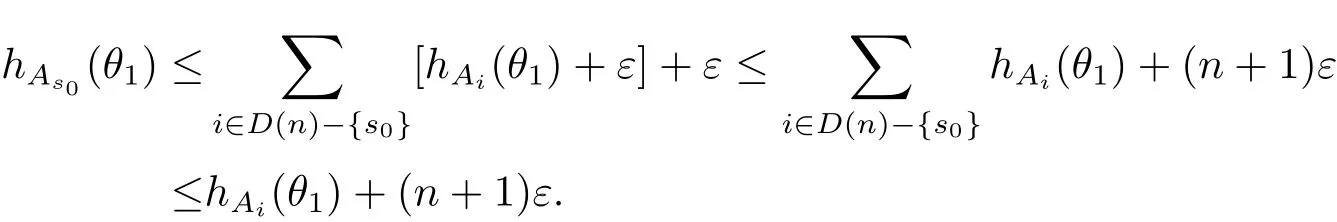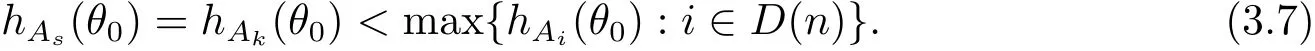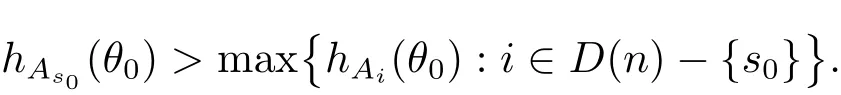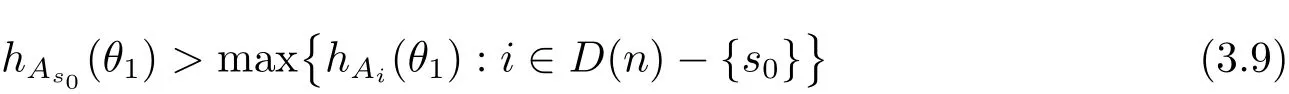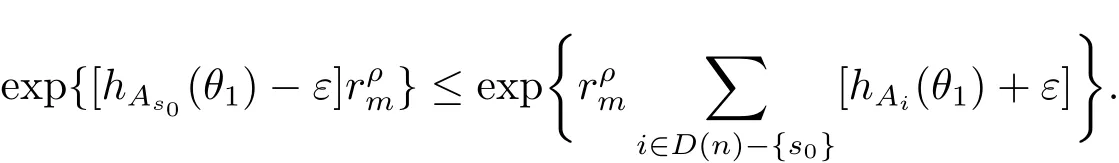关于一类高阶性线差分方程亚纯解的增长性
吴秀碧,张石梅,龙见仁,2,石 磊
(1.贵州师范大学数学科学学院,贵州贵阳 550001)
(2.北京邮电大学计算机学院;理学院,北京 100876)
1 引言及结果
近年来,有大量的文献关注复差分方程的亚纯解的增长性问题,例如参考文献[1]和[2]等.本文主要考察以下形式的线性差分方程
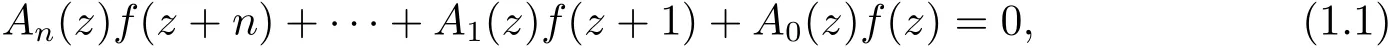
其中Aj(z)(j=0,···,n)均是整函数.
2008年,Chiang和Feng研究了方程(1.1)解的增长性,并给出了其解增长级的一个下界估计.
定理A[3]设Aj(z)(j=0,···,n)均为多项式,且存在l:0≤l≤n使得max{deg(Pj):0≤j≤n,j≠l} 同时,他们还考虑了方程系数为超越整函数的情形,也给出了方程解的增长级的下界估计. 定理B[3]设Aj(z)(j=0,···,n)均为整函数,且存在l:0≤ l≤ n使得max{ρ(Aj):0≤ j≤ n,j≠l}< ρ(Al).如果f(z)是方程(1.1)的任意非零亚纯解,则必有ρ(f)≥ρ(Al)+1. 当系数都是多项式时,称次数等于max{degPj(z):0≤j≤n}的系数为主导系数;当系数有超越整函数时,称增长级等于max{ρ(Aj(z):0≤j≤n}的系数为主导系数.注意到定理A和定理B的共同点就是都只有一个主导系数.如果方程拥有多个主导系数时,是否还有相应结论?这个问题引起很多研究人员的关注.2011年,陈宗煊考虑了这个问题,在弱化定理A的条件下,得到如下定理. 定理C[2]设系数P0(z),···,Pn(z)均为多项式,且满足Pn(z)P0(z)0和 如果f(z)是方程(1.2)的任意非零解亚纯解,则必有ρ(f)≥1. Laine和Yang改进了定理B,并证明了以下结果. 定理 D[4]假设Aj(z)(j=0,···,n)均为有穷级整函数,wj(j=0,···,n)为任意复常数,且型最大的主导系数仅有一个.记ρ=max{ρ(Aj):0≤j≤n},则方程 的任意非零解都满足ρ(f)≥ρ+1. 同时,Laine和Yang还提出如下问题. 问题 如果方程型最大的主导系数不止一个,定理B或定理D的结论是否还成立? 2015年,Heittokangas[5]等应用Phragmén-Lindelöf指标函数来研究二阶微分线性微分方程解的增长性,得到很多结果.受到文献[5]的研究方法的启发,本文利用指标函数研究高阶线性差分方程问题,为此先回顾Phragmén-Lindelöf指标函数的定义. 对于一个有穷正级整函数g(z),其指标函数定义为 如果g(z)的型有限,则hg(θ)是一个连续有上界的函数.且对任意ε>0,易知 为了方便叙述起见,我们引入以下符号.对于n+1个有穷正级的整函数Aj(j=0,···,n),ρ =max{ρ(Aj):0 ≤ j ≤ n},记主导函数指标集为 D(n),即 D(n)={j:ρ(Aj)=ρ},并用|D(n)|表示D(n)的元素个数. 本文得到如下几个结果. 定理1.1 设Aj(z)(j=0,···,n)是有穷正级整函数且至多有一个为无穷型,wj(j=0,···,n)为任意复常数,记ρ=max{ρ(Aj):0≤ j≤ n}.如果方程 有一个非零解f(z)满足ρ(f)< ρ+1,则对于任意的θ∈[−π,π),要么max{hAi(θ):i∈D(n)}≤0,要么存在s,k∈D(n)使得 如果方程(1.5)的所有系数的增长级都相同时,我们得到下面的结果. 定理1.2 设Aj(z)(j=0,···,n)是有穷正级整函数且至多有一个为无穷型,wj(j=0,···,n)为任意复常数,记ρ=max{ρ(Aj):0≤ j≤n}且|D(n)|=n+1.如果方程(1.5)有一个非零解f(z)满足ρ(f)<ρ+1,则对于任意的θ∈[−π,π),必存在s,k∈D(n)使得 由以上两个定理及其证明过程,容易得到以下推论. 推论 1.3 设Aj(z)(j=0,···,n)是有穷正级整函数且至多有一个为无穷型,记ρ=max{ρ(Aj):0≤j≤n},如果存在θ0∈[−π,π)和某个s0∈D(n)满足下列三个条件之一 那么方程(1.3)的每个非零解f(z)都满足ρ(f)≥ρ+1. 为了证明上述定理,需要如下的几个引理. 引理1[3]设η1,η2是任给的两个复数,f(z)是一个有穷级的亚纯函数,则对于任意给定的正数ε,必有相应的性线测度为零的集合E⊂[0,2π)且当θ∉E时,必存在正常数R0=R0(θ)>1,当z满足argz=θ和|z|≥R0时,有 引理2 设A(z)和B(z)为整函数且满足下列条件之一 (1)ρ(B)< ρ(A)∈ (0,+∞)且 hA(θ)≥ 0; (2)ρ(B)= ρ(A)∈ (0,+∞)且 hA(θ)>0 ≥ hB(θ); (3)ρ(B)= ρ(A)∈ (0,+∞)且 hA(θ)≥ hB(θ)>0. 则有 同时由hA(θ)的定义可得,对任意ε>0,有 于是结合(2.2)和(2.3)式便有 由于ε的任意性便得结论. 当A(z)和B(z)满足条件(2)或者条件(3)时,类似(2.3)式有 从而由(2.3)和(2.4)式,并注意到hB(θ)−hA(θ)≤0,于是有 同理由于ε的任意性便得结论. 引理3 设A(z)为有穷正级且型有穷的整函数,f(z)是亚纯函数且满足ρ(f)<ρ(A)+1.则对任意给定η1,η2和充分小的ε>0,必有相应的性线测度为零的集合E⊂[0,2π)且当θ∉E,存在正常数R0=R0(θ)>1,当z满足argz=θ和|z|=r充分大时,有 同时由hA(θ0)的定义可得有 由(2.5)和(2.6)式便知 注意到ρ(A)>ρ(f)−1+ε,于是当r充分大时就得引理结论. 定理1.1的证明 根据D(n)的定义可知D(n)非空且元素多于一个,否则由定理C便得方程(1.3)的每一个非零解都满足ρ(f)≥ρ+1.易知对于任意i∈D(n),Ai(z)都为有限型.若不然,假设存在i0∈D(n)使得Ai0(z)为无穷型,但由定理条件可知,无穷型的系数至多只有一个,于是由定理D可得,方程(1.3)的每一个非零解都满足ρ(f)≥ρ+1,这都得到了矛盾. 现假设定理的结论不成立,即存在θ0∈[−π,π),有max{hAi(θ0):i∈D(n)}>0且对于任意s,k∈D(n),要么 要么 注意到不管是(3.1)式成立还是(3.2)式成立,都必定存在s0∈D(n)使得下式成立 于是由引理1便知存在至多n个零测集Ei(0≤i≤n,i≠s0),对于任意 都能找到R0=R0(θ)>1,使得当|z|=r≥R0时,有 其中w0=0.由于Ai(z)(i∈D(n))都是有限型,故hAi(θ)(i∈D(n))都是连续函数.注意到是一个零测度集,结合(3.3)式便知存在使得下列不等式成立 同时,改写方程可以得到 于是由引理2可得 这与(3.5)式矛盾. 如果 δ≤ 0.对于 ∀i∈ D(n)−{s0},j∈ {0,1,2,···n}−D(n),设 则存在点列rm使得 根据引理3可得 不等式右边第二项移到左边,整理后得 由于hAs0(θ1)−ε>0和ρ>ρ(f)−1+ε,于是当rm充分大时,有 两边取对数并注意到δ≤0,故有 定理1.2的证明 现假设定理的结论不成立,即存在θ0∈[−π,π),对于任意s,k∈D(n),要么 要么 注意到不管是(3.6)式成立还是(3.7)式成立,都必定存在s0∈D(n)使得下式成立 和 成立.设δ=max{hAi(θ1):i∈D(n)},若δ>0,证明方法完全类似于定理(1.1). 若 δ≤ 0,∀i∈ D(n)−{s0},设则存在点列rm使得 根据引理3可得 注意到δ≤0,结合(3.9)式便有
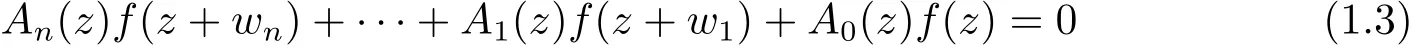
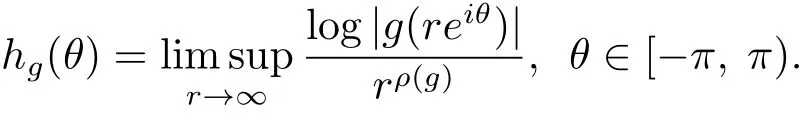


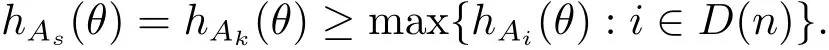
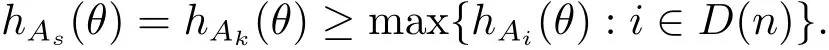
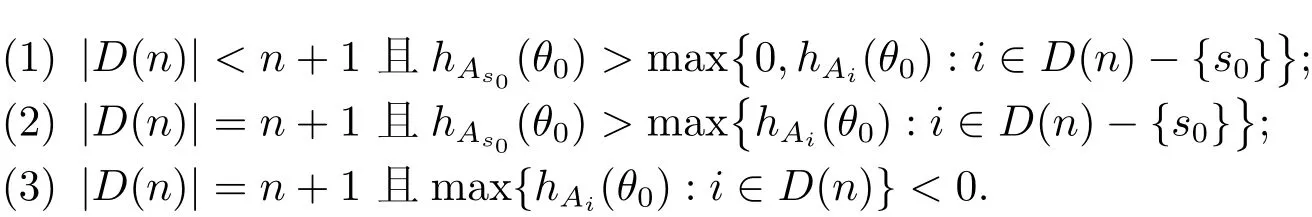
2 引理
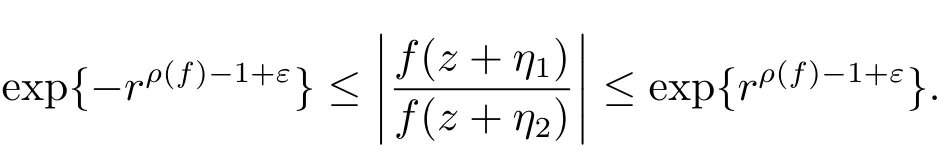
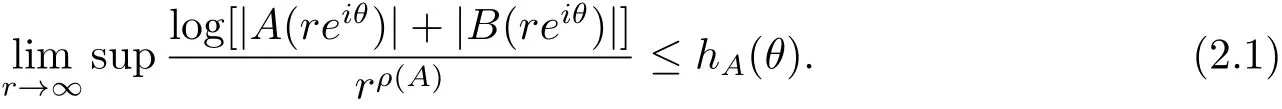


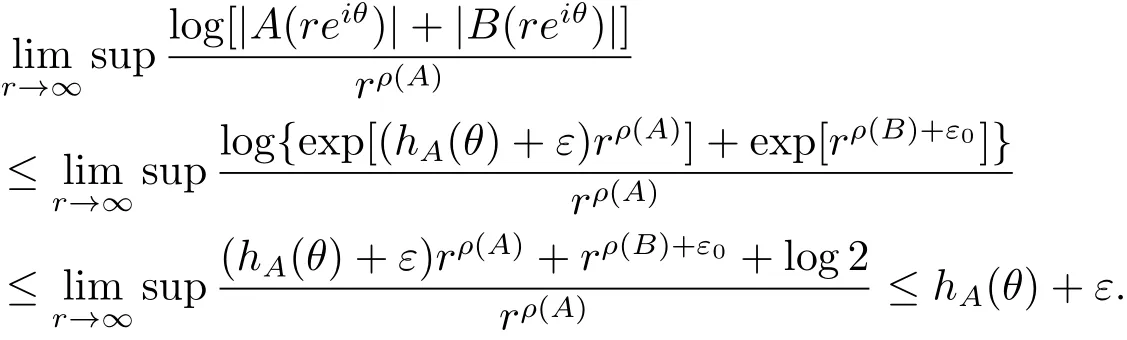
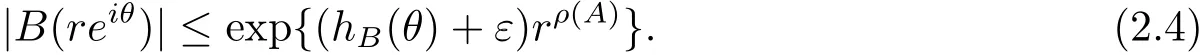
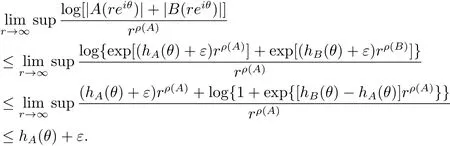
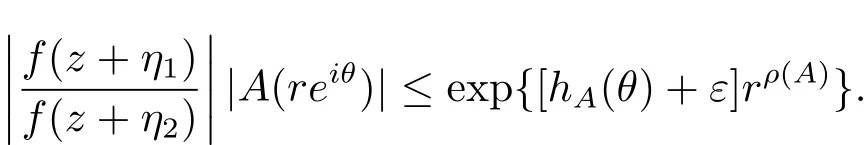
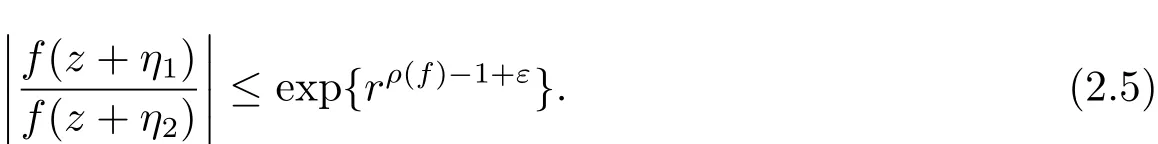
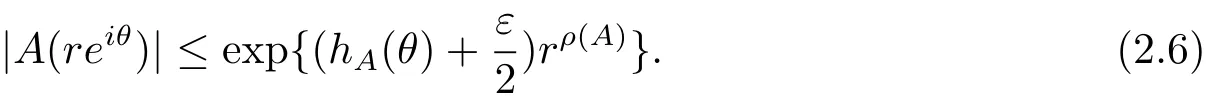
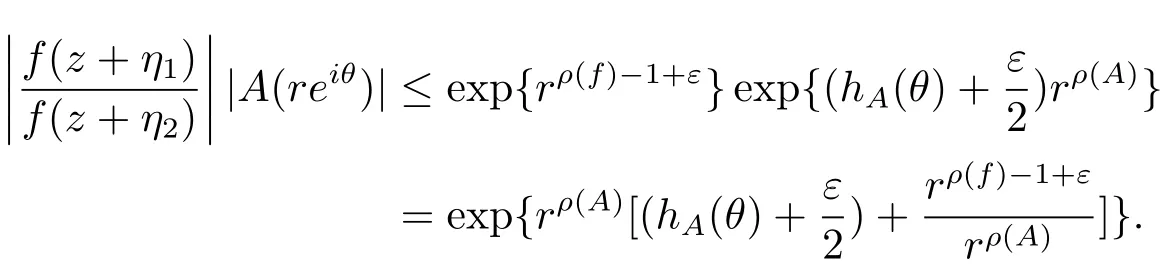
3 定理的证明