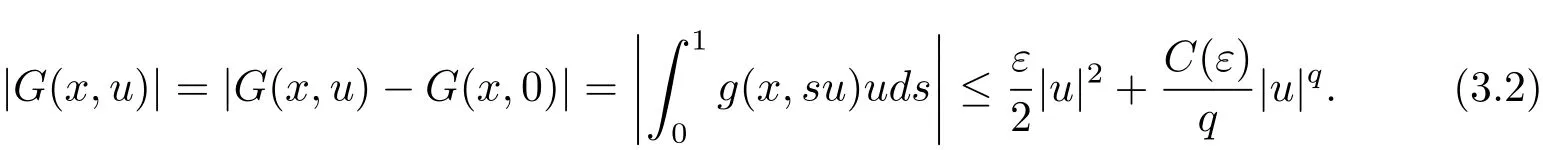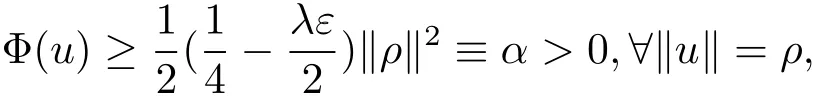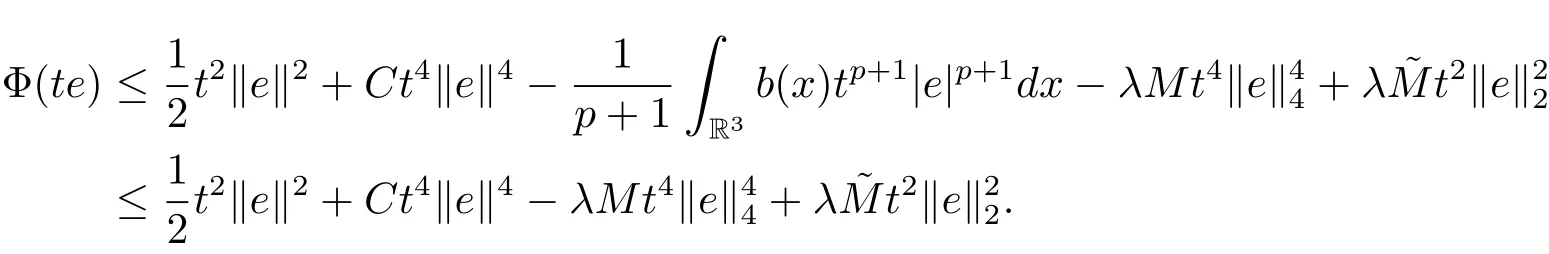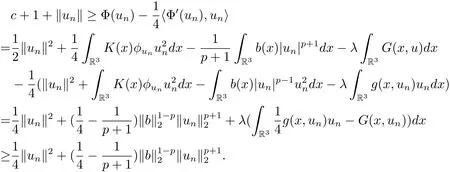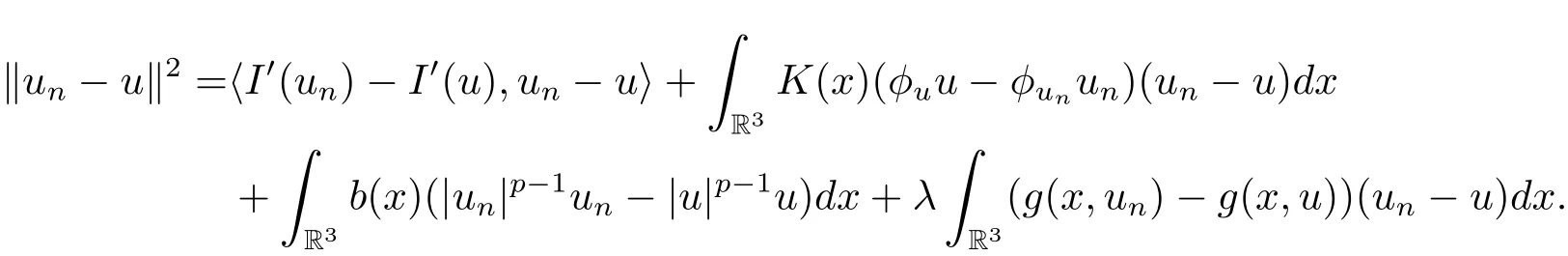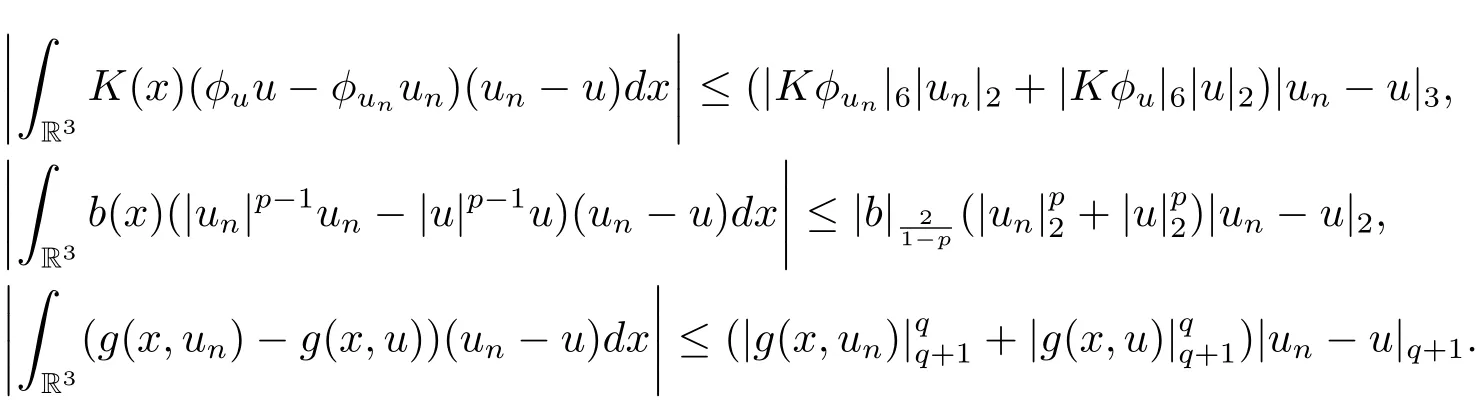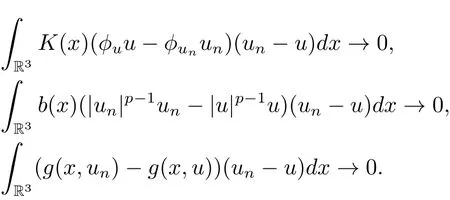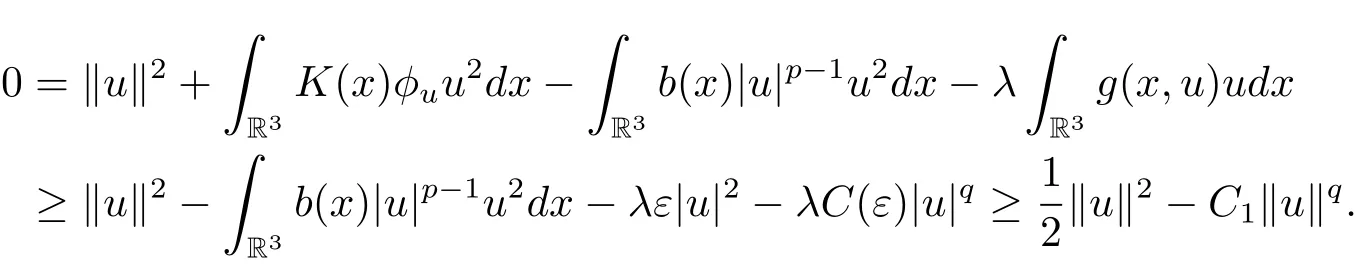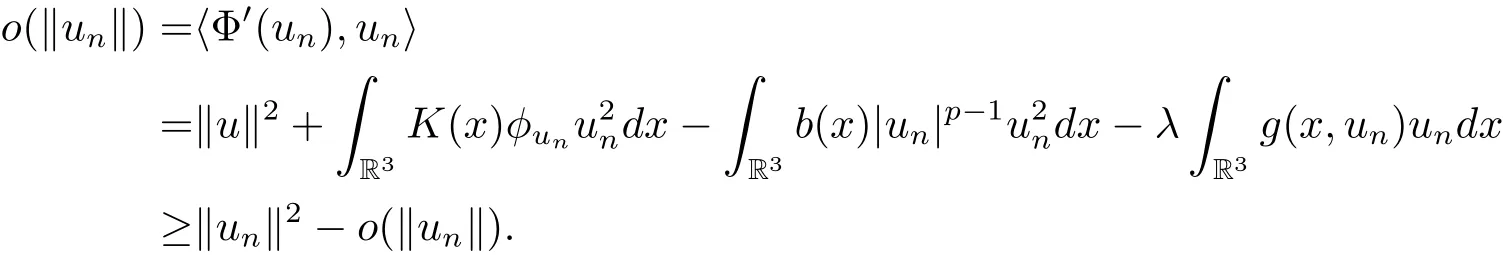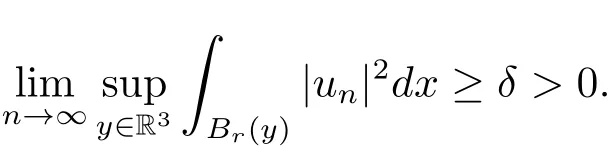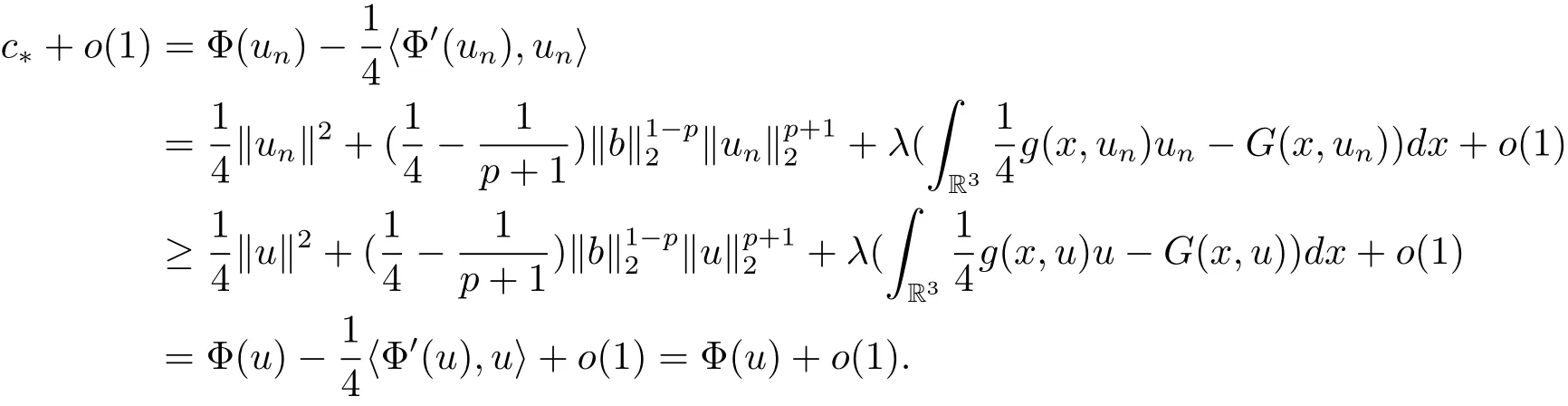一类非线性Schrödinger-Maxwell方程基态解的存在性
汪敏庆,黄文念,方立婉
(广西师范大学数学与统计学院,广西桂林 541006)
1 引言及主要结果
考虑以下非线性Schrödinger-Maxwell方程基态解的存在性.
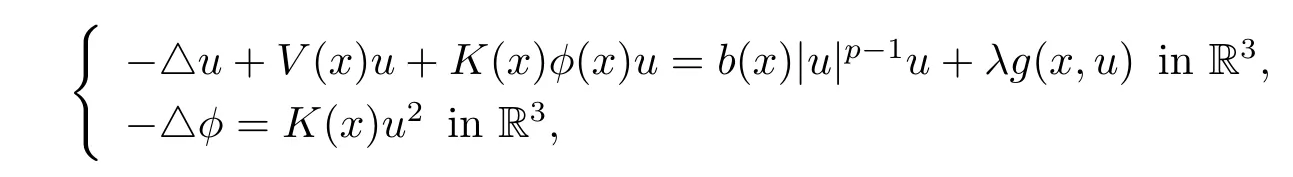
这样的方程又被称为Schrödinger-Poisson方程.在量子力学中,该方程可描述带电粒子与电磁场的相互作用(关于物理方面的更多的描述可详见文献[1]).
过去的几十年里,在临界点理论和变分法的帮助下,类似于系统(1.1)的系统的解的存在性、不存在性和多重性得到了广泛的研究,具体可参考文献[2–4].进一步地,当V(x)≡K(x)≡1,f(x,u)=|u|p−1u,1 对V,K,b,g有以下假设 (V)V(x)∈C1(R3,R),V(x)≥ a1>0,其中a1>0是一个常数.对每一个M>0,meas{x∈R3,V(x)≤M}<∞. (K)K ∈L∞(R3,R),对任意的x∈R3,有K(x)≥0. (B)b:R3→R+是一个正连续函数,并且,其中 0 (g1)g(x,u)∈C(R3×R,R),g在xi(i=1,2,3)中是1-周期的,且|g(x,u)|≤C(1+|u|q−1),其中 2 (g2)当u→0时,对所有的x∈R3,有g(x,u)=o(u). (g3)当u→∞时,对所有的x∈R3,有 (g4)对任意的(x,u)∈(R3,R),有其中G(x,u) 对于系统(1),主要的结果如下 定理 1.1 假设(V),(K),(B),(g1)–(g4)成立,则系统(1.1)存在一个基态解,其中C>0表示一系列不同的正常数. 定义下列函数空间H1(R3)={u∈L2(R3)|∇u∈(L2(R3)3}.对应的范数为 定义函数空间D1,2(R3):={u∈L2∗(R3):∇u∈(L2(R3)3}.对应范数为 令 则E是一个Hilbert空间,对应的内积为 记∥·∥为Ls(R3)下的范数,H=为H(R3)空间中径向函数的子空间,则H 可以紧嵌入Ls(R3),其中s∈(2,6)[16].再记 则E是连续嵌入到Ls(R3)中的,s∈[2,2∗],这里的2∗=6是在三维空间里Sobolev嵌入的临界指数.因此,存在一个常数C>0,使得 其中 是在Lebesgue空间Ls(R3)下的范数. 因为K ∈L∞(R3,R),故对每一个u∈E,由Hölder不等式,有 由Lax-Milgram 定理(详见文献[11])可知,对任意的u∈E,存在唯一的ϕu∈D1,2(R3),使得 对于ϕu,可以写成下列积分形式 故由x∈R3,K(x)≥0可知,ϕu(x)≥0.结合(2.1)和(2.2)式,有 因此由Hölder不等式和(2.1)式,有 定义泛函I:E→R 从上面的讨论可知I是C1的,并且I的临界点就是问题(1.1)的解.进一步地,由(2.3)式有 如果u∈E 是泛函Φ的一个临界点(也就是Φ′(u)=0),则(u,ϕu)是系统(1.1)的一个解.进一步地,对任意的u,v∈E,有 特别地, 定义对应的 Nehari流形为 N={u ∈ E:⟨Φ′(u),u⟩=0}.设 (X,∥·∥)为 Hilbert空间,{ej}为其一组标准正交基,令 定义2.1设E是一个实Banach空间,Φ∈C1(E,R),c∈R.当n→∞,un∈E时,如果对任意满足 的序列{un}⊂X都有收敛的子列,则称Φ满足(PS)c条件. 为了证明定理1.1,我们将会利用以下形式的山路定理(详见文献[12,13,14]). 定理2.2[12,13,14]设E是一个实Banach空间,Φ∈C1(E,R),Φ(0)=0,对任意的c>0,Φ满足满足(PS)c条件,且 (i) 存在 ρ,α >0,使得 Φ|∂Bρ≥ α; (ii)存在e∈EBρ,使得Φ(e)≤0.则Φ有一个临界值c≥α. 引理2.3[15]对任意的2≤s<2∗,有 引理3.1 若(V),(K),(B),(g1)–(g4)成立,e∈E{0},则 (i) 存在 ρ,α >0,使得 Φ|∂Bρ≥ α. (ii)当|t|→∞,Φ(te)=−∞. 证 (i)由假设(g1),(g2)可知,对任意的ε>0,存在C(ε)>0,使得对所有的x∈R3,u∈R,有 因此,由中值定理,有 由引理2.3及p∈(0,1)可知,存在Re>0,使得当∥u∥≥Re时,有 于是,对于u ∈ Zk,∥u∥≥ Re,有 您可通过以下三种方式关注《临床神经病学杂志》微信公众平台:1、搜索公众订阅号名称“临床神经病学杂志”添加关注;2、搜索微信号“lcsjbx”添加关注;3、扫描位于本刊目次页右上角的微信二维码。 (ii)由(g3)可知,对任意的M>0,存在ξ=ξ(M)>0,使得对所有的x∈R3,|u|>ξ,有 由(g1),(g2)可知,存在M1=M1(M)>0,使得对所有的x∈R3,0<|u|≤ξ,有 由(3.6)式和中值定理可知,对所有的x∈R3,|u|≤ξ,有 引理3.2若(V),(K),(B),(g1)–(g4)成立,则Φ满足(PS)c条件. 证 设序列{un}⊂E�满足Φ(un)→c>0,Φ′(un)→0.当n充分大时,有 再由p∈(0,1)可知,{un}在E中有界. 在E中不妨设un弱收敛到u,则在Ls(R3)(s∈(2,6))中,un强收敛到u,且有 显然 ⟨I′(un)− I′(u),un− u⟩→ 0.由 Hölder 不等式,有 由Sobolev不等式及E可以连续嵌入到Ls(R3)(s∈(2,6))中可知 因此∥un−u∥2→0. 引理3.3假设(V),(K),(B),(g1)–(g4)成立,则对任意的u∈E{0},存在tu>0,使得tuu∈N. 证 对任意给定的u∈E{0},由引理3.1中的(ii)可知,存在Re>0,使得当∥te∥≥Re时,有Φ(te)<0.同理,由引理3.1中的(i)可知,对于t>0足够小时,有Φ(tu)>0.因此,0 引理3.4存在α0>0,使得对所有的u∈N,有∥u∥≥α0. 证 因为u∈N,故⟨Φ′(u),u⟩=0.令ε>0足够小,则有 因此 ∥u∥ ≥ α0>0,u∈N,其中 引理3.5[16]设r>0,如果{un}在H1(R3)中有界,且 则对于任意的s∈(2,6),在Ls(R3)中有un→0. 定理1.1的证明 设{un}⊂N 是Φ的一个极小化序列,且满足(PS)c条件,则∥un∥有界.令,则δ>0.如若不然,则δ=0.由引理3.5可知,对任意的s∈(2,6),在Ls(R3)中有un→0.从而当n→∞时,有 因此有 故∥un∥→0,这与引理3.4相矛盾,故δ>0.因此存在r,δ>0,{yn}⊂Z3,使得 由(V),(g1)可知,存在u∈N,使得un⇀u≠0,则Φ′(u)=0.由于u∈N,所以Φ(u)≥c∗.事实上,由(g4),Fatou’s引理(见文献[17]),∥·∥的弱下半连续和{un}有界,可得 所以 Φ(u)≤ c∗,因此证毕.2 预备知识及相关引理
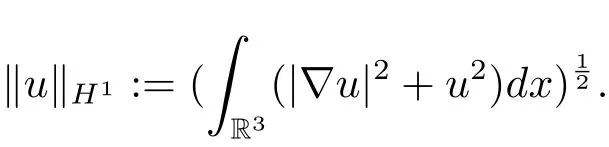
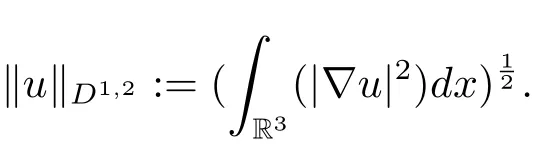
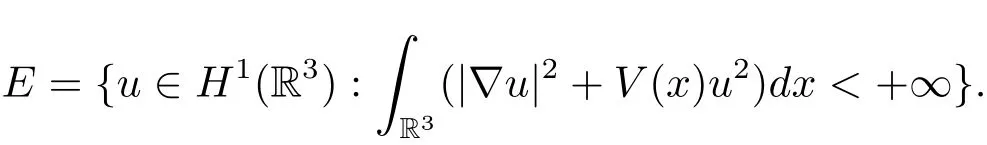
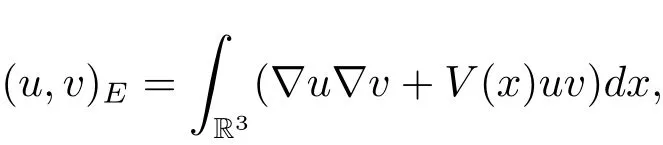
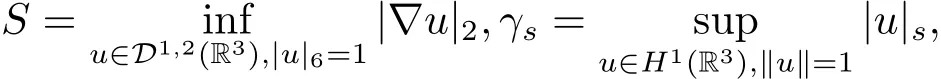

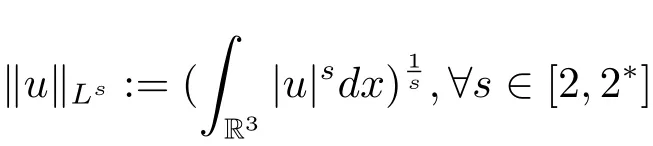
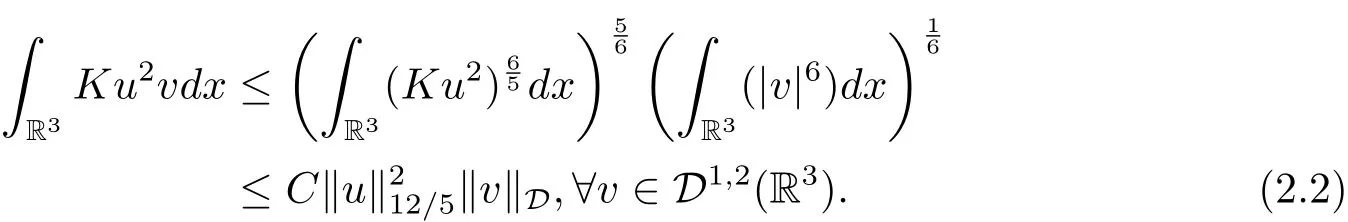

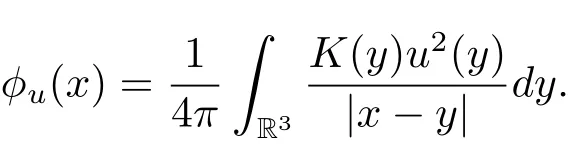
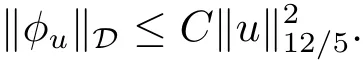
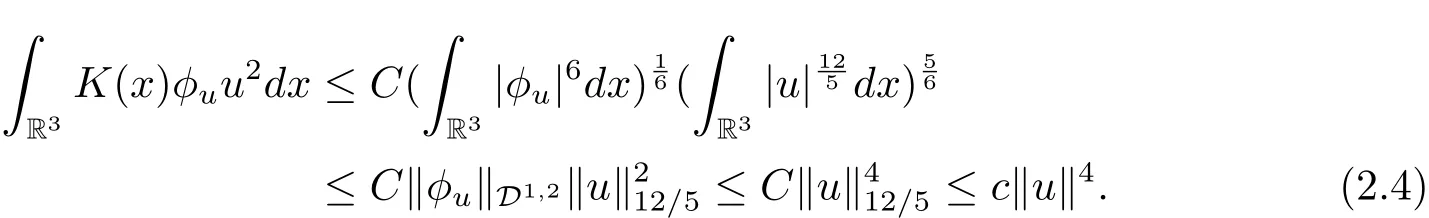
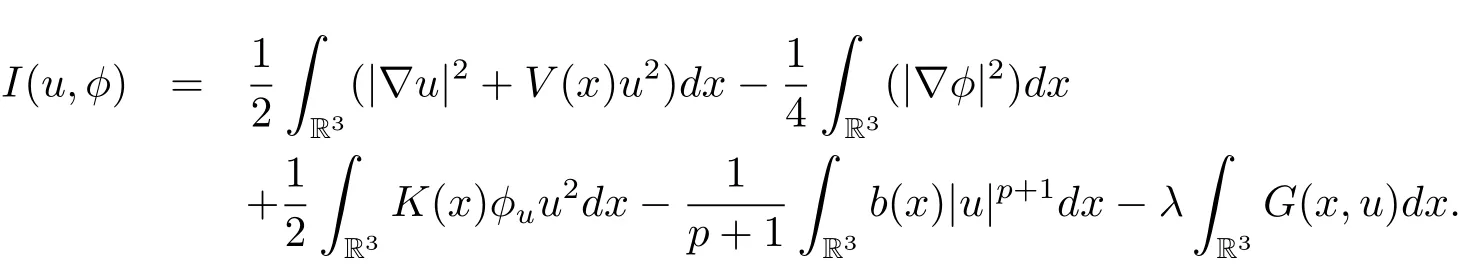
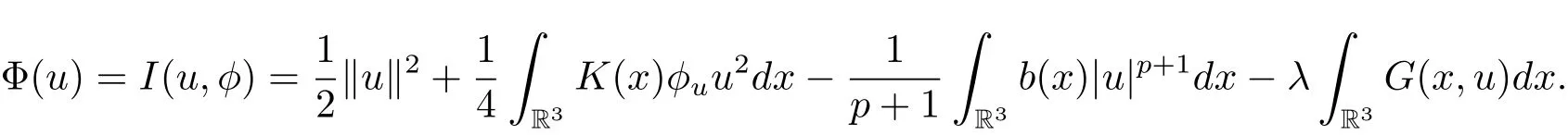
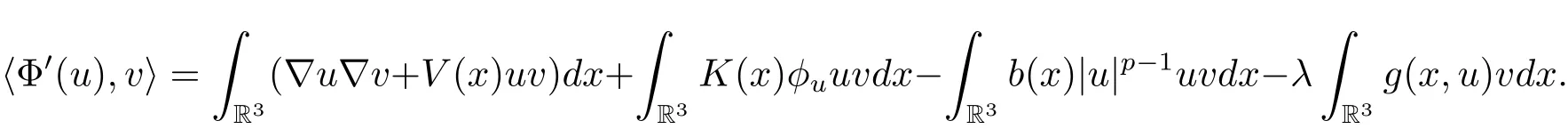
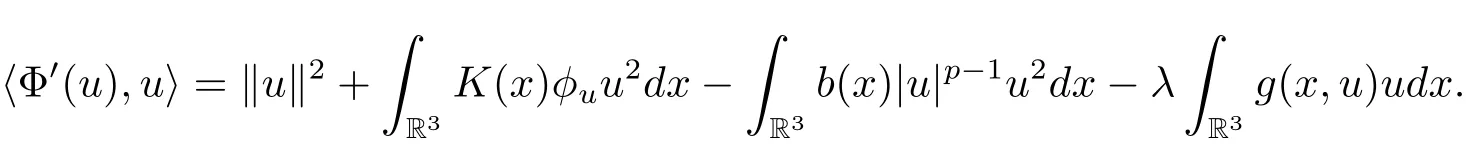
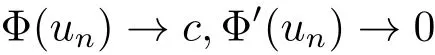
3 定理1.1的证明