Poisson方程的一维最优系统和不变解

白月星,苏道毕力格

(内蒙古工业大学理学院,内蒙古呼和浩特 010051)

1 引言

在现代经济学和物理领域中求解偏微分方程(PDEs)的解常常是困难的,因此求解PDEs显得至关重要.Lie对称是公认的普适性最广的方法之一,Lie群是研究微分方程的对称性并求出其解析解的强有力工具,一个主要应用是寻找群不变解[1–5].利用给定对称群的任意子群求解相应的特征方程,可以把原方程约化为自变量更少的方程.对称群的每个子群都对应着一组群不变解,然而这样的子群似乎总有无穷多个,要列出所有可能的群不变解几乎是不可能的.要找到这些完整且不等价的群不变解,也就需要对所有的群不变解进行分类.对这个问题,Ovsiannikov和Olver分别发展出一些系统有效的方法,由此引入了“最优系统”的概念.构建最优系统有很多方法,如Ovsiannikov利用伴随表示的矩阵法构建最优系统[6],Petera发展了一种很重要的方法,已经广泛的应用到物理学中[7,8].目前国内外研究者对其进行研究,推动了最优系统的发展[9–15].

应用对称方法的前提是确定PDEs拥有的各类对称.Lie算法把确定对称的问题转化为确定对应无穷小向量的问题,而该无穷小向量是由满足确定方程组的无穷小生成函数确定.完成这个过程将涉及到大量、复杂的机械化计算.研究发现,微分形式的吴方法是有效克服Lie算法缺陷的方法之一.近年来,朝鲁教授推广建立了微分形式的吴方法,即吴-微分特征列集算法[16,17].该算法主要考虑控制计算过程中符号堆积及易于在软件Mathematica中实现的问题,使吴方法的应用从纯代数理论推广到微分情形,发展了吴方法.我们知道如果直接得到微分方程(组)的全部对称群是非常困难的,并且传统Lie算法中未能考虑未知量的序关系,导致计算机上的无穷循环及工作量大等许多困难,而这些问题由吴-微分特征列集算法得到部分解决.目前,吴-微分特征列集算法成功的应用在PDEs的古典对称、非古典对称、高阶对称、近似对称、势对称、守恒律和对称分类等问题上,取得了优异的成果,促进了PDEs对称理论的研究[18–23].我们基于该算法研究了对称方法在NLPDE边值问题中的应用[24,25].最近,朝鲁等人利用该算法研究了Lie代数的最优系统.

本文利用Lie对称方法研究了Poisson方程的单参数李对称群和群对应的伴随表达式,在此基础上构建了该Lie对称群的一维最优系统,并利用一维最优系统中的元素对Poisson方程进行对称约化,确定不变解及其精确解.具体过程:首先,利用吴-微分特征列集算法和符号计算软件Mathemetica,计算Poisson方程对应的古典对称;其次,计算换位子、伴随算子,通过伴随方法构建该方程的一维最优系统;最后,确定古典对称所对应的不变解以及精确解,丰富了Poisson方程的精确解.

2 Poisson方程的一维最优系统

2.1 Poisson方程的对称

考虑Poisson方程

假设方程(2.1)对应的对称向量为

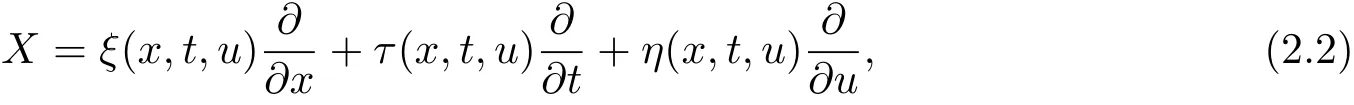
其中ξ(x,t,u),τ(x,t,u),η(x,t,u)为该对称的无穷小生成函数.根据Lie算法可以得到方程(2.1)的对称对应的确定方程组,但是很难手动求解.基于吴-微分特征列集算法,应用该算法的Mathematica程序包进行计算得到与确定方程组等价的特征列集对应的方程组,即

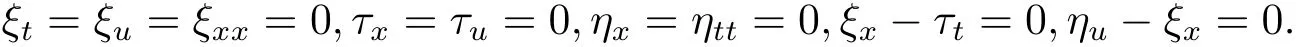
求解上面的方程组,得到无穷小生成函数

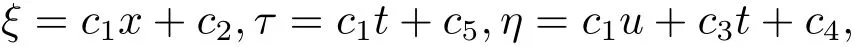
其中c1,c2,c3,c4,c5是任意常数,则无穷小向量为

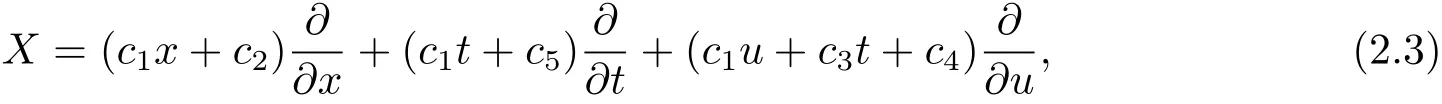
所以方程(2.1)有5个单参数古典对称,其对应的无穷小向量为

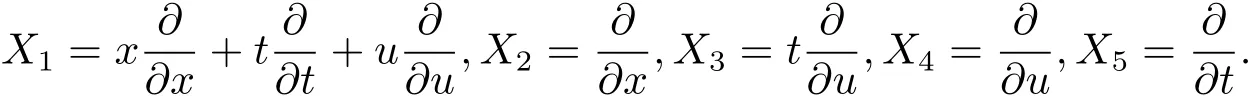
2.2 Poisson方程的一维最优系统

在上一部分中得到了无穷小生成向量,下面构造一维最优系统.

定义1无穷小生成元Xα,Xβ的换位子是一阶算子

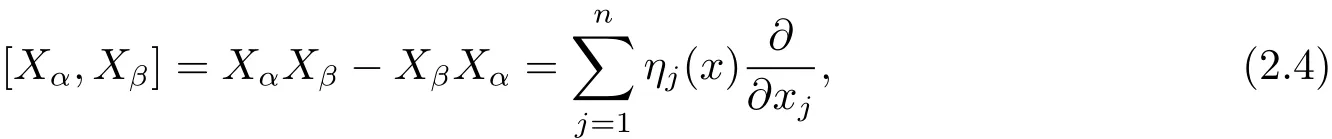
其中

因此得到 [Xα,Xβ]=−[Xβ,Xα].

定义2设G是Lie对称群,g是G对应的Lie代数,对于每一个v∈g,伴随算子Adv关于w∈g,有

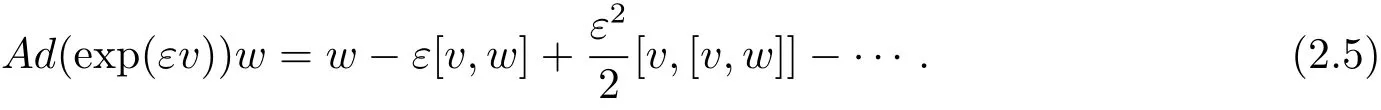
根据定义1和定义2,可以计算方程(2.1)所拥有的Lie对称构造一维最优系统.

表1:换位子表

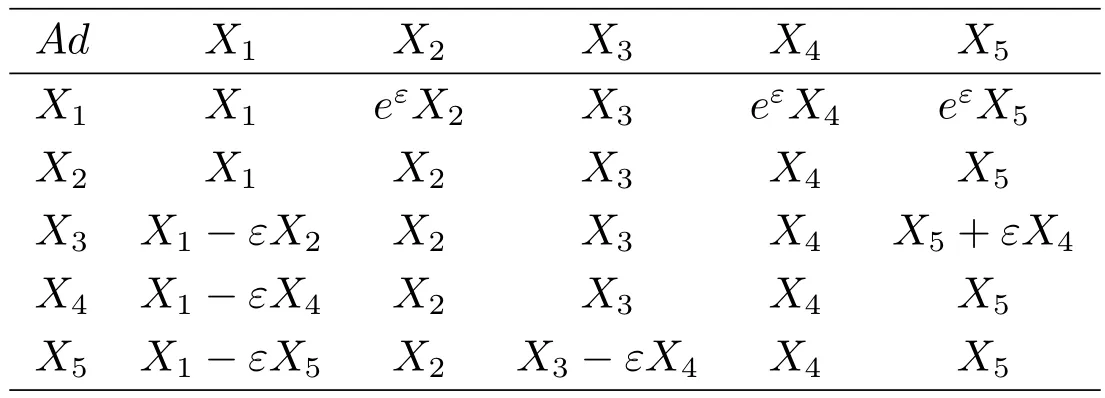
表2:伴随关系表

根据求一维最优系统的方法,设一个非零的X∈L5,L5是构成Lie代数

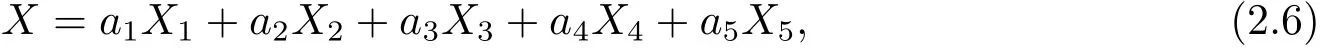
其中a1,a2,a3,a4,a5是任意常数.

(1)假设 a1≠0,不失一般性.令 a1=1,则X=X1+a2X2+a3X3+a4X4+a5X5.为了使X2消失,利用伴随算子X′=Ad(exp(εX3))X,通过计算有

令 ε=a2,则有

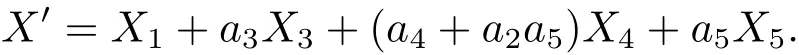
下一步将 Ad(exp(εX5))作用于 X′,有 X′′=Ad(exp(εX5))X′,通过计算有

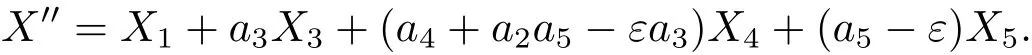
为了消去 X5,令 ε=a5,有X′′=X1+a3X3+(a4+a2a5−a3a5)X4.将 Ad(exp(εX4))作用于 X′′,有 X′′′=Ad(exp(εX4))X′′,通过计算有

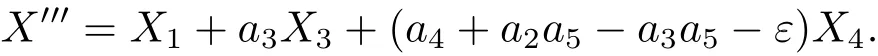
为了消去 X6,令 ε=a4+a2a5−a3a5,有X′′′=X1+a3X3.由上式知不能再继续利用伴随算子.

(2)假设 a1=0,a5≠0,不失一般性.令 a5=1,则X=a2X2+a3X3+a4X4+X5.为了使X4消失,将伴随算子Ad(exp(εX3))作用于X,有

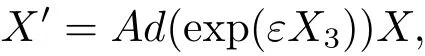
通过计算有

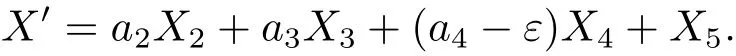
令ε=a4,则有X′=a2X2+a3X3+X5.由上式知不能再继续利用伴随算子.

(3)假设 a1=a5=0,a2≠0,不失一般性.令 a2=1,则X=X2+a3X3+a4X4.为了使X4消失,将伴随算子Ad(exp(εX5))作用于 X,有X′=Ad(exp(εX5))X,通过计算有

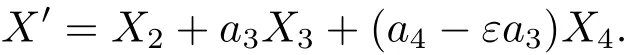
(4)假设 a1=a2=a5=0,a3≠0,不失一般性.令a3=1,则X=X3+a4X4.为了使X4消失,将伴随算子 Ad(exp(εX5))作用于X,有X′=Ad(exp(εX5))X,通过计算有

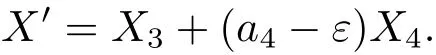
令ε=a4,则有X′=X3.由上式知不能再继续利用伴随算子.

(5)假设 a1=a2=a3=a5=0,a4≠0.不失一般性,令 a4=1,则X=X4.由上式知不能再继续利用伴随算子.

综上得到方程(2.1)的一维最优系统为

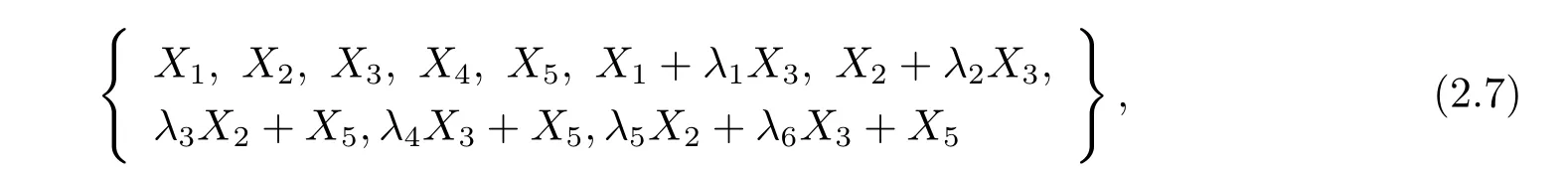
其中 λi(i=1···6)是任意常数.

3 Poisson方程的不变解

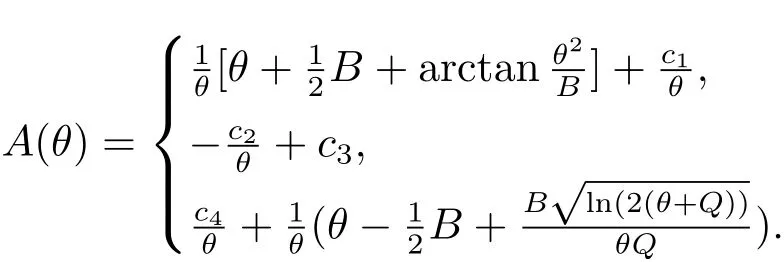
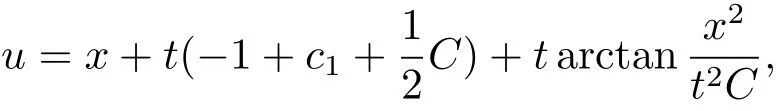
1.下面计算古典对称

对应的Lie变换群.X1+X3对应的初值问题为

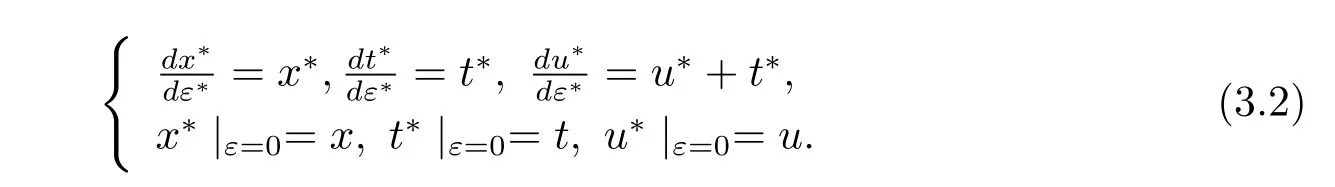
通过求解(3.2)式,得到对应的单参数Lie变换群如下

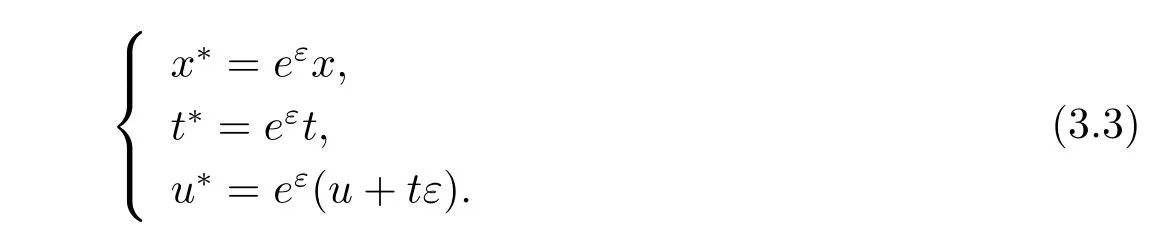
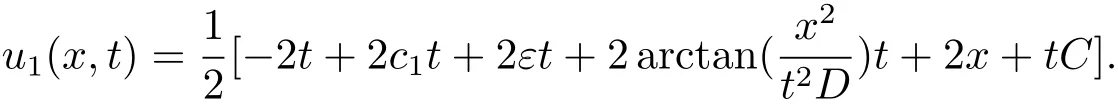
2.通过古典对称

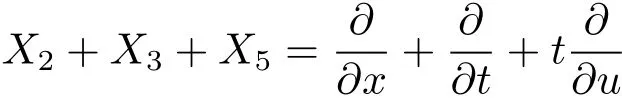
对应的单参数Lie变换群为

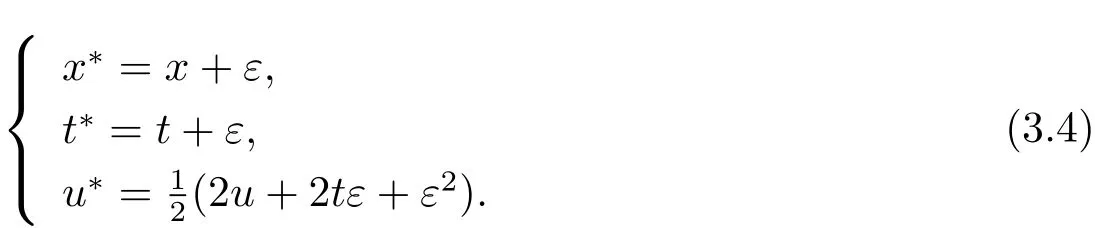
将Lie变换群(3.4)作用于该情况的不变解u1(x,t),得到

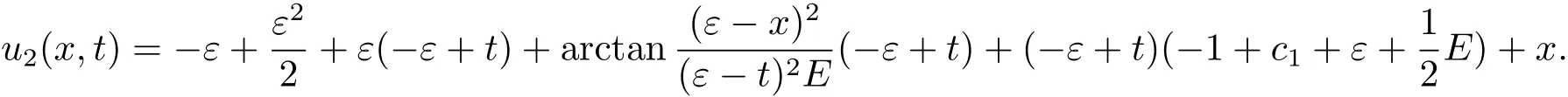
其中,以上得到的精确解都是对应方程的新解,因篇幅有限,其它情况在本文中不进行讨论.

4 本文结论

偏微分方程(PDEs)的求解经常出现在物理、工程力学等研究领域中.随着科技的进步,推动了求解PDEs的持续发展,目前计算PDEs的不变解显得尤为重要.本文通过应用吴-微分特征列集算法和Mathematica软件,获得了Poisson方程的对称和Lie代数的一维最优系统,并且计算了最优系统中对应元素的Lie变换群.将所得的Lie变换群作用于不变解得到了新的精确解,达到了丰富Poisson方程的精确解的效果.