零膨胀计数数据回归模型的选择与比较及R语言的实现*

刘振球　严　琼　左佳鹭　方绮雯　张铁军△

【提　要】　目的　探讨和比较不同模型在零膨胀数据回归分析中的应用。 方法　在R语言中，拟合HIV合并血友病数据的对数线性模型、零膨胀模型、随机森林、决策树以及支持向量机模型，通过比较标准化均方误差和均方根误差，对模型进行评价与选择。结果　从标准化均方误差和均方根误差来看，随机森林是对原始数据拟合的最好的模型，随后是支持向量机和决策树模型，而经典的计数模型表现则相对较差。结论　在对零膨胀计数资料进行回归预测时，机器学习方法的效果优于经典的计数模型。

在医学研究中，经常遇到因变量为计数资料的问题，如一段时间内癫痫患者的抽搐发作次数、某种化疗药物引起患者的呕吐次数等。这些事件发生次数取值为非负整数，且多服从正偏态分布。研究此类问题时，我们通常假设事件发生次数服从Poisson分布，将该关注事件发生的频数作为因变量，拟合广义线性Poisson回归模型，去探索其他自变量对该事件的影响[1]。当事件发生次数过度离散时，我们可以选择负二项回归模型。但是，在某些罕见事件的研究中，常遇到许多观察个体在研究时间内，并未发生该结局事件，因此数据中会有相当比例的结局变量取值为零，并且零的比例超过Poisson回归和负二项回归的预测能力，故称为零膨胀[2]。Lambert首次建立了零膨胀Poisson回归模型[3]。该模型的提出，有效地解决了零膨胀数据的分析问题，使分析结果更加准确。近年，关于零膨胀计数资料的模型选择问题已成为一个研究热点，各种模型层出不穷，比如Hurdle计数模型[4]，半连续数据两部模型等[5]。此类模型均是基于经典的统计方法，虽然能够用明确的数学表达式对原始数据进行展示和解释，但是由于受限于原始数据的结构以及对原始数据的一些假设，因此在对未知数据进行预测时，往往效果不好。随着计算机技术的不断发展，机器学习方法也被越来越多地运用到实际问题的处理过程中。以往的研究证实，在时间序列数据的预测上，算法模型，比如随机森林、支持向量机、决策树等，其预测效果明显优于传统的统计模型[6-7]。

本研究拟比较不同的算法模型以及传统的统计模型，在零膨胀数据预测分析上的优劣，从而为零膨胀数据的分析提供一个新的思路。

方法与实例分析

本文所采用的分析数据来自于美国国家癌症研究所资助的多中心血友病队列研究(http://www.stat.berkeley.edu/users/statlabs/labs.html)。该项研究从1978年1月1日到1995年12月31日在欧美16个治疗中心跟踪随访了超过1600个血友病病人，所得数据共有2144个观测值及6个变量。表1为变量的基本描述。

表1　HIV合并血友病数据变量基本描述

在上述变量中，deaths是一个零膨胀变量，其取值分布如图1所示。

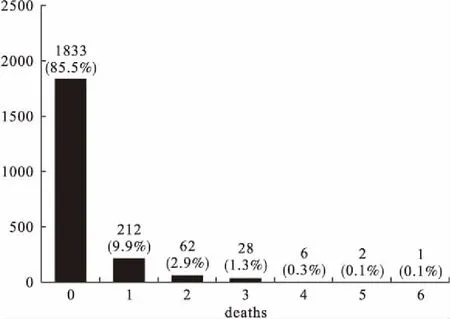
图1　deaths变量取值分布

死亡数等于零的组占比为85.5%，因此，该数据为典型的零膨胀数据。在经典统计学的基础上，我们一般采用零膨胀计数数据模型对其进行回归。该模型由两个部分构成，一部分为集中在零点的点质量，如logistic或者probit回归模型；第二部分为某种计数分布，比如Poisson分布或者负二项分布。以零膨胀Poisson模型为例，其密度函数可以表示为：

p(yi=0|xi)=pi+(1-pi)exp(-μi)

(1)

(2)

上式中，yi为某事件发生数，xi为协变量向量，μi为第i个个体的期望Poisson计数，pi为二项分布产生的零计数概率。零膨胀负二项分布的概率分布与零膨胀Poisson分布模型类似，二者第一部分相同，而在非零部分选用了负二项分布。

R语言pscl包中的zeroinfl()函数可用来拟合零膨胀负二项分布模型、零膨胀Poisson模型，以及零膨胀几何分布模型。

该函数基本格式如下：

fit_zero <- zeroinfl(deaths～hiv+factor+py+age | hiv+py+age,data,dist)

管道符“|”将模型分为两个部分，前面是零部分，后面是非零部分，至于每一部分用什么变量进行拟合，无法先验确定，可以通过多次尝试来决定。该函数默认是进行零膨胀Poisson回归，我们可以根据dist参数选择相应的非零部分的分布模型。

关于选择何种分布模型，我们可以使用过度离散检验[8]和Vuong检验[9]来决定，与之对应的函数分别是odtest()和vuong()。除此之外，我们也可以利用AIC，BIC，标准均方误差以及均方根误差等统计指标作为判断标准。

零膨胀Poisson回归模型得出的结果见表2。

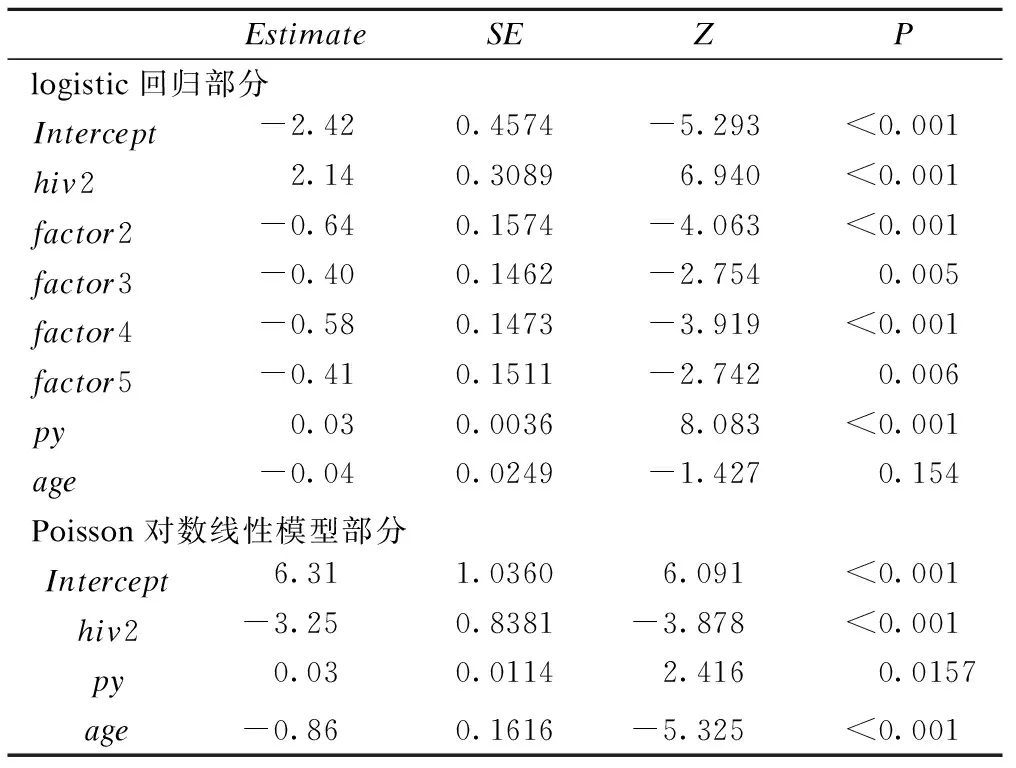
表2　零膨胀Poisson回归模型结果

为了比较不同的模型，包括经典的计数模型以及机器学习模型，对于该数据的拟合情况，采用标准均方误差(NMSE)以及均方根误差(RMSE)作为判断标准，对各个模型进行评价。NMSE和RMSE的计算公式如下：

(3)

(4)

在模型拟合的过程中，为了保证结果的稳健性，采用了10重交叉验证，最后对NMSE和RMSE取均值。实现这一过程的函数见附件。该自定义函数命名为zero_fl，包含9个参数，分别为data，model，formula，id，tar，z=10，p=0.8，dist=′poisson′，seed=2017；其含义分别为：

(1)data：传入的数据集。

(2)model：选择的模型，接受一个字符串，比如”rf”，表示进行随机森林拟合。

(3)formula：针对不同模型的回归公式。

(4)id：接受一个正整数，表示根据这个变量对原始数据集进行均衡切分。

(5)tar：接受一个正整数，表示目的变量。

(6)z：默认值为10，表示进行10重交叉验证。

(7)p：默认值是0.8，表示进行交叉验证时，将80%的数据设置为训练集。

(8)dist：表示进行零膨胀模型时，采用何种分布，可选“poisson”，“bioneg”和“geometric”。

(9)seed：默认是2017，用于设置随机数种子。

该函数最终返回的是NMSE和RMSE。对于本文中使用的数据集，最终不同模型拟合的结果如图2和表3所示。

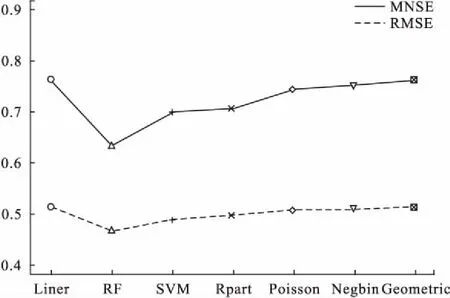
Liner:Poisson对数线性模型；RF：随机森林；SVM：支持向量机；Rpart：决策树模型；Poisson：Poisson零膨胀模型；Negbin：负二项分布零膨胀模型；Geometric：几何分布零膨胀模型

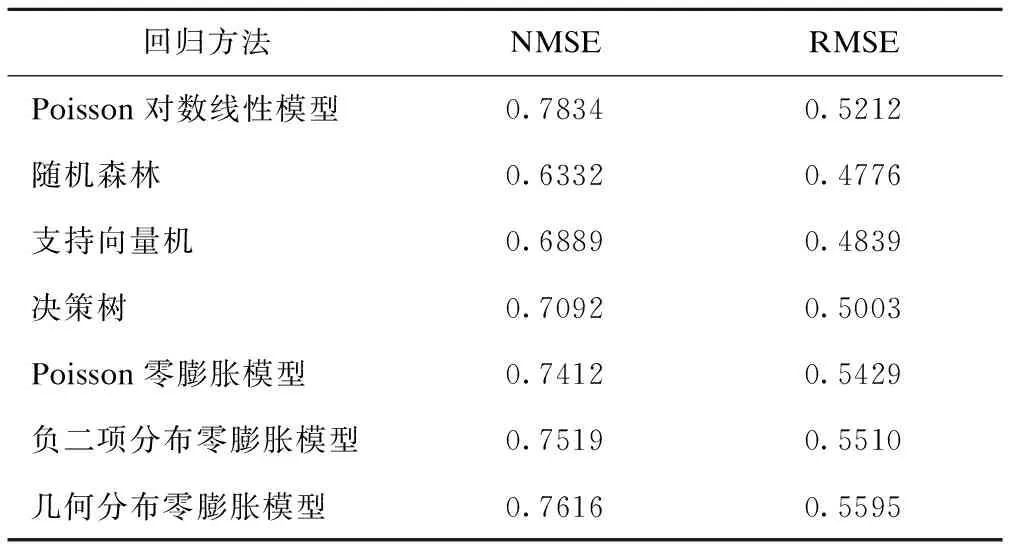
图2　不同模型拟合结果比较

小　　结

计数数据是我们在医学科研中经常遇到的一个问题，对于此类问题，常用的方法是广义Poisson对数线性模型[10]。但是对于因变量中零过多的情况，传统的统计模型则不能对数据进行很好的拟合，从而造成数据信息使用不全，导致偏离甚至错误的结论。零膨胀模型的提出很好地解决了这个问题，我们可以根据原始数据的特征，比如零在结局变量中所占的比例，选择相应的零膨胀模型；也可以对多个不同的零膨胀模型进行统计学比较，从而选择最优模型。

从上文中的结果来看，专门为计数资料设计的若干经典统计模型的表现整体不如广谱的算法模型。拟合程度最好的是随机森林，随后是支持向量机和决策树模型，表现最差的是Poisson对数线性模型，零膨胀模型介于此二类模型之间。这提示我们今后在处理零膨胀数据时，如果需要对每一个自变量进行解释，则可以选择合适的零膨胀回归模型，如果需要对未知数据进行预测，机器学习方法是一个更好的选择。

经典的统计模型与算法模型存在本质区别，前者通常要求数据满足若干假设，如果数据满足所有假设，则经典模型会拟合出完美的结果，数学上也能被精确描述，我们从而能够根据模型对数据和结果作出正确的解释。而机器学习算法不基于原始数据的任何假设，因此适用范围更加广泛。这些方法预测精度高，但是不会得到类似P值那样的显著性度量指标，也无法用精确的数学公式来描述，更不会用诸如无偏性等概念来评价模型，所以交叉验证的方法被广泛用于评价算法模型。本文中提供的R语言代码，简单实现了对不同模型的10重交叉验证，有助于我们快速得到准确的结果。