加载方式对节点受剪承载力公式的影响分析

朱贞贞杨红，2赵雯桐

（1.重庆大学土木工程学院 400045；2.重庆大学山地城镇建设与新技术教育部重点实验室 400045）

引言

钢筋混凝土梁柱节点是结构的重要传力部位，受力机理复杂，对梁柱组合体进行低周反复加载试验是研究节点抗震性能的主要方法［1］。根据外荷载的加载点位置不同，梁柱组合体试验可分为柱端加载试验和梁端加载试验两大类。

部分学者采用柱端加载方式研究节点的抗震性能，如史庆轩等［2］通过柱端加载试验研究了高强材料对节点抗震受剪承载力的影响；北山和宏等［3］通过柱端加载试验研究了节点核心区抗剪箍筋对节点抗震受剪承载力的影响。也有相当多学者采用梁端加载方式进行研究，如傅剑平等［4］通过梁端加载试验研究了剪压比对节点抗震受剪承载力的影响，Park等［5］通过梁端加载试验分析了新、美两国设计规范中节点抗震受剪承载力的差异。

梁柱组合体低周反复试验结果是评价节点抗震性能、校核节点受剪承载力的基础。各国规范建立节点抗震受剪承载力计算公式时，一般并未区别加载方式对试验结果的影响。我国《混凝土结构设计规范》（GB 50010-2010）［6］的节点受剪承载力计算公式主要依据20世纪70年代末框架节点专题研究组所完成的梁柱组合体梁端加载低周反复试验的结果建立［7］，并采用国内其他试验研究结果进行修订后而形成。

为研究梁柱组合体试验加载方式对GB 50010-2010的节点抗震受剪承载力计算公式的影响，本文首先从节点受剪机理、节点最大作用剪力计算方法两个角度分析了加载方式的影响，然后收集了大量柱端加载、梁端加载梁柱组合体试验结果，经对比计算和统计分析，研究了节点试验加载方式对GB 50010-2010的节点受剪承载力计算公式的影响规律。

1 加载方式对节点受剪承载力影响的机理分析

在柱端加载、梁端加载试验中，梁柱组合体试件的外荷载P、柱轴力N的施加位置以及边界约束条件如图1所示。

柱端加载试验中，梁柱组合体的变形特征与地震作用下框架结构的梁、柱变形规律相似，能够真实反映地震作用下P-Δ效应的影响；梁端加载试验中，其边界条件易于满足，可更准确地测量柱顶水平反力Pb，但其加载装置较复杂，且不能真实反映地震下的P-Δ效应。

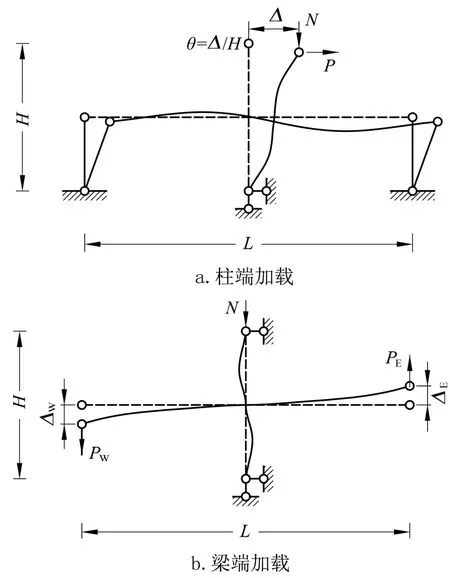
图1 梁柱节点加载方式示意Fig.1 Loading methods of beam-column joint

柱端加载试验一般以层间位移角为加载控制条件，并在柱顶施加往复水平外荷载P［8］。

梁端加载试验通常先以力为加载控制条件，在节点左、右两侧，一侧的梁远端施加向上的外荷载PW，另一侧的梁远端施加向下的外荷载PE，分别测得梁上部、下部纵筋屈服时的梁端竖向位移后，再以该位移为加载控制条件，实施往复加载［4］。

图2给出了节点内的两种剪力传递机构［9］。如图2a所示，节点通过梁、柱端受压区混凝土的压力形成斜压杆机构；在图2b中，节点通过节点内抗剪箍筋、柱纵筋和混凝土形成桁架机构。

梁柱组合体的加载方式不同，将导致梁柱节点内形成的斜压杆机构的几何尺寸、形状出现差异（见图3）。以最常见的非对称配筋框架梁为例（通常梁上部纵筋明显多于下部纵筋），暂仅分析梁内纵筋屈服时刻的受力特征。

在柱端加载的试验中，仅梁的下部纵筋出现屈服（梁上部纵筋的配筋面积更多，其屈服时刻更晚），此时节点左、右梁端弯矩相近，故节点两侧梁边缘的混凝土受压区高度也相近≈），其斜压杆形状见图3a。

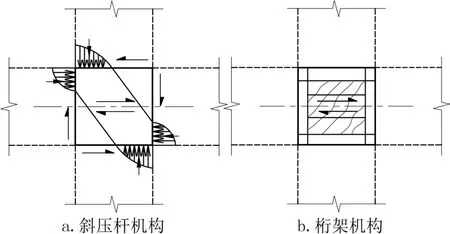
图2 节点承力机构Fig.2 Shear resisting system

图3 不同加载方式的斜压杆机构Fig.3 Strut mechanism under different loading methods

在梁端加载试验中，加载制度（如前所述）要求梁的上部纵筋、下部纵筋同时屈服，故节点左、右梁端弯矩相差较大，从而导致节点两侧梁边缘的混凝土受压区高度出现较大差异，即，其斜压杆形状见图3b。

在极限承载力时刻，梁柱组合体构件的斜压杆形状也会因为梁端截面混凝土受压区高度的不同而产生差异。

节点受剪承载力除与斜压杆有关外，桁架机构也有贡献。梁、柱纵筋在节点区的粘接性能是桁架机构发挥剪力传递作用的主要影响因素，但纵筋在节点内的锚固长度、混凝土轴心抗压强度、钢筋屈服强度、节点轴压比、节点剪压比、节点配箍特征值等参数均对梁、柱纵筋在节点区的粘接性能有影响，其规律较为复杂，因此直接采用理论分析的方法考察加载方式对桁架机构的影响规律较为困难。

赵雯桐等［10］基于6个中间层中间节点的试验数据，采用细化有限元方法对加载端滞回曲线特征以及贯穿节点核心区的梁纵筋在节点内的粘结滑移变形、节点区的非线性剪切变形的计算结果进行了校核，并仔细分析了同一梁柱组合体试件分别采用梁端加载、柱端加载两种试验方式时节点非线性反应（即梁纵筋在节点内的粘结滑移、节点区的剪切变形）的差别，研究结果表明，加载方式会直接影响梁纵筋在节点内的粘接特征，并进一步影响桁架机构的剪力传递规律。

综上所述，不同加载方式下，节点内斜压杆的形状、尺寸不同，该差异将直接影响节点受剪承载力的大小。

2 加载方式对节点作用剪力计算方法的影响

根据梁柱组合体试验的结果，可直接计算梁柱节点在试验过程中承受的最大作用剪力。但随着加载方式不同，节点作用剪力的计算方法也有明显差异。

在柱端加载试验中，柱顶水平反力、水平位移、梁端反力等可直接进行测量；梁端加载试验中，直接进行测量的是柱顶水平反力、梁端反力、梁端位移等。根据这些参数的实测试验数据，可进一步计算节点在试验过程中承受的剪力。

如图4所示，按力平衡条件，水平方向的节点作用剪力Vj［11］为：

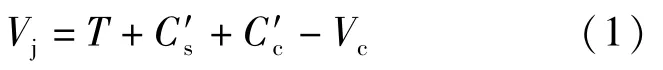
式中：T为贯穿节点的梁上部纵筋在节点边缘的拉力；C′s为梁上部纵筋承担的压力；C′c为混凝土承担的压力；Vc为节点上边缘的柱剪力。

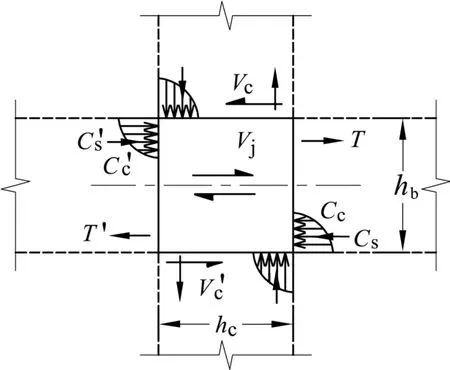
图4 中间层中间节点剪力Fig.4 Joint shear force in interior RC beam-column joint

由于T、C′s和C′c难以在试验中直接测量，故很多学者［12］建议按照式（2）计算Vj：

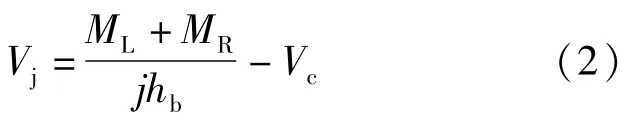
式中：ML、MR分别为节点左、右的梁端弯矩；j为力臂系数；hb为梁截面高度；jhb整体表示为梁端截面受压区合力中心到受拉合力中心的距离。

对于柱端加载试验，式（2）可转化为：

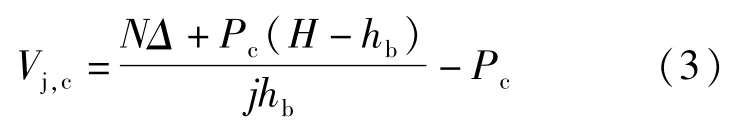
式中：Vj，c为柱端加载试验的节点作用剪力；N为柱顶施加的轴压力；Δ为柱顶水平位移；Pc为柱端加载试验的柱顶水平力；H表示柱上、下铰结点之间的距离。

对于梁端加载试验，式（2）可转化为：

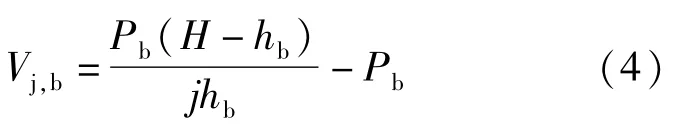
式中：Vj，b为梁端加载试验的节点作用剪力；Pb为柱顶水平支座反力。

对比式（3）、式（4）可知，几何参数、材料参数完全相同的梁柱组合体试件，由于加载方式不同，梁柱节点在试验过程中承受的作用剪力必然存在一定程度的差别，差异的大小主要与NΔ有关，同时Pc、Pb的测量结果差异对节点承受的作用剪力也有一定影响。

式（3）、式（4）的差异是由图1所示的试验装置、加载方式不同造成的。因此，即使对于同一梁柱组合体试件，分别采用梁端加载、柱端加载方法对其进行试验，得到的梁柱组合体的节点作用剪力Vj试验结果必然存在差异。

3 节点受剪承载力计算结果对比分析

3.1 试验参数的统计

梁柱组合体试件采用不同加载方式进行试验将导致节点作用剪力Vj的试验结果出现不同，而梁柱组合体的低周反复试验结果是各国规范建立节点受剪承载力计算公式的基础。因此，本文将重点分析加载方式对我国《混凝土结构设计规范》（GB 50010-2010）的节点受剪承载力计算公式的影响。

本文共收集了58个中间层中间节点梁柱组合体低周反复加载的试验数据。其中，柱端加载试件30个、梁端加载试件28个，其参数分布见表1。所有梁柱组合体试件均没有楼板和平面外正交梁，且节点内均配有抗剪箍筋。

表1 试件参数分布Tab.1 Ranges of parameters of specimens

试件的最终破坏模式包括以下三种，即：梁内纵筋未屈服、仅节点发生剪切破坏（JF）；梁内纵筋屈服，最后节点发生剪切破坏（BYJF）；仅梁内纵筋屈服，节点未发生显著剪切破坏（BY）。在所收集的58个梁柱组合体试件中，合计有5个柱端加载试件为JF破坏模式；20个柱端加载试件、25个梁端加载试件为BYJF破坏模式；5个柱端加载试件、3个梁端加载试件为BY破坏模式（因节点受剪未到达极限承载力，故统计分析不包括此种破坏模式的试验结果）。

图5给出了所收集的两种加载方式试验中，各试件的设计参数与规范GB 50010-2010的节点抗震受剪承载力计算公式（9度一级抗震、其他情况两者的计算公式不同，具体详下节）之间的分布关系。由图5可知，大部分构件的设计参数皆分布在GB 50010-2010的公式所表示的直线附近，离散较小，表明收集的试验数据具有较好的研究和统计意义。

3.2 规范的节点抗震受剪承载力计算公式

《混凝土结构设计规范》（GB 50010-2010）［6］的节点抗震受剪承载力计算公式包含节点混凝土、节点区箍筋两项，其抗震受剪承载力视为两项作用之和。

图5 试件设计参数与规范节点抗剪公式关系Fig.5 Relationship between the parameters of specimens and the shear resistance formula

对于9度设防的一级抗震框架：

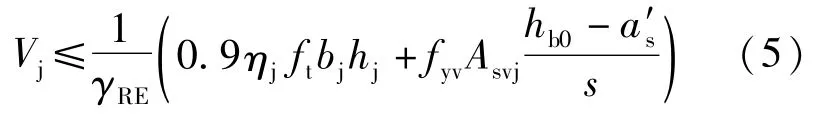
对于其他情况：

式中：γRE为承载力抗震调整系数，取0.85；ηj为正交梁对节点的约束影响系数，对于平面梁柱节点可取1.00；ft为混凝土轴心抗拉强度设计值；bj为框架节点核心区的截面有效验算宽度；hj为框架节点核心区的截面高度；fyv为横向钢筋的抗拉强度设计值；Asvj为核心区有效验算宽度范围内同一截面验算方向箍筋各肢的全部截面面积；s为横向钢筋的间距；N为对应于考虑地震组合剪力设计值的节点上柱底部的轴向力设计值；bc为该侧柱截面宽度；hb0为梁截面有效高度；a′s为梁纵向受压钢筋合力点至截面近边的距离。

基于上述收集到的各梁柱组合体试件的几何参数、材料物理力学性能参数，以及力、位移的实测试验结果，本文进行了以下计算分析：

（1）按式（3）或式（4）计算得到整个循环加载位移下的节点作用剪力试验结果，然后取其最大值作为节点的极限剪力（即节点最大作用剪力）。

（2）根据GB 50010-2010的节点受剪承载力计算公式进行计算，除bj、hj、bc等几何参数，以及Asvj和s，N按试验实际取值确定外，ft按试件的实测节点区混凝土立方体抗压强度进行换算，fyv按节点箍筋的实测抗拉强度取值。

（3）最后将以上两步的计算结果进行比较，并定义以下节点剪力比值系数：

式中：Vjc，test、Vjb，test分别表示柱端加载试件、梁端加载试件的节点最大作用剪力试验结果（即第1 步的结果）；Vj，cal表示根据GB 50010-2010 公式计算的柱端加载试件、梁端加载试件的节点抗震受剪承载力（即第2步的计算结果）。

Vjc，test、Vjb，test、Vj，cal以及ξc和ξb的计算结果见表2，表3给出了ξc和ξb的统计结果。

由表3可知，统计量ξc和ξb的离散系数Cv均小于0.40［26］，故本文用于分析的梁柱组合体试验样本的均值μ可有效反映母体特征，可据此统计结果对GB 50010-2010的节点抗震受剪承载力计算公式进行分析。

图6是将两种加载方式下各梁柱组合体试件的节点剪力比值系数计算结果均分别按照从大到小进行排序后得到的ξc和ξb的分布。

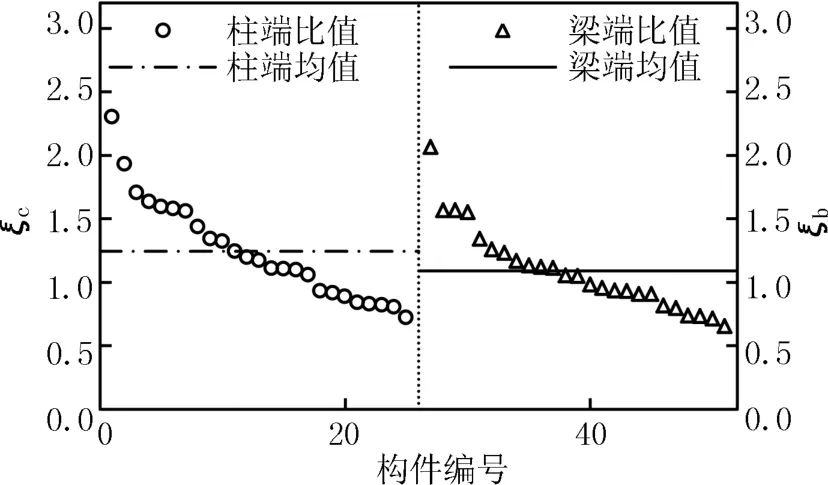
图6 节点剪力比值系数分布Fig.6 Distribution of the ratio coefficient

结合表3和图6的结果可知：

（1）在表3中，ξb的方差σ2=0.110小于ξc的方差σ2=0.157，即梁端加载试验的计算结果的离散性更小。

（2）梁端加载试件的节点剪力比值系数ξb的均值μ=1.091（见表3），这表明GB 50010-2010的节点抗震受剪承载力计算公式得到的计算结果与梁端加载试验的节点最大作用剪力测量结果是较为相符的（ξc的均值μ=1.245）。据此可合理推测，《混凝土结构设计规范》（GB 50010-2010）依据试验结果建立、校核节点抗震受剪承载力计算公式时，其数据库是以梁端加载梁柱组合体试验为主。

表2 节点剪力比值系数计算结果Tab.2 The results of the joint shear force ratio coefficient

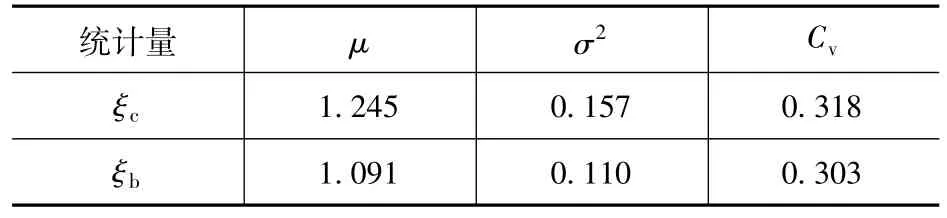
表3 节点剪力比值系数统计结果Tab.3 The statistical characteristics of the joint shear force ratio coefficient

（3）柱端加载的节点剪力比值系数ξc从总体上明显大于梁端加载试件的ξb（见图6），表3中的ξb的均值μ=1.091也明显小于ξc的均值μ=1.245，即柱端加载试件的节点剪力比值系数从总体上比梁端加载试件大15%左右。

（4）ξc的均值μ=1.245，表明柱端加载试件的节点最大作用剪力较GB 50010-2010的节点抗震受剪承载力公式计算结果大约25%。如前所述，柱端加载试验中，由于梁柱组合体变形特征与地震作用下框架结构的梁柱组合体变形规律相似，也能够更真实反映地震作用下的P-Δ效应，因此，对于实际结构的梁柱节点，采用GB 50010-2010的节点受剪承载力公式进行配箍计算，得到的设计结果是偏保守的。

4 结论

本文从节点受剪机理、节点作用剪力计算方法分析了加载方式导致的节点受剪作用的差异，基于收集的试验数据，研究了加载方式对《混凝土结构设计规范》（GB 50010-2010）的节点受剪承载力计算公式的影响，并得到以下结论：

1.梁柱组合体试件可采用梁端加载、柱端加载两种方式，加载方式不同，节点区的斜压杆尺寸、节点剪力计算方法、试验过程中节点承受的剪力均有差异。

2.GB 50010-2010的节点抗震受剪承载力公式的计算结果更符合梁端加载试验的节点最大作用剪力的测量结果，梁端加载试验的节点剪力比值系数离散性更小。

3.柱端加载试件的节点剪力比值系数从总体上比梁端加载试件大15%左右。

4.柱端加载时梁柱组合体的变形特征与地震下实际结构的梁柱变形规律相似，同时能够较真实反映P-Δ效应。

5.实际结构的梁柱节点采用GB 50010-2010的节点受剪承载力公式进行配箍计算的设计结果是偏保守的。